Neurones en 5 minutes

Permettez-moi d'ajouter les lignes «machine learning» et «neural networks» à votre CV en 5-10 minutes de lecture et de compréhension d'un court article? Pour ceux qui sont loin de la programmation, je dissiperai tous les mythes sur la complexité de l'IA et montrerai que la plupart des projets d'apprentissage automatique sont construits sur des principes extrêmement simples. Allons-y - nous n'avons que cinq minutes.

Prenons l'exemple le plus élémentaire des réseaux de neurones - les perceptrons; Moi-même, après cet exemple, j'ai pleinement compris le fonctionnement des réseaux de neurones, donc si je ne me trompe pas, et vous pouvez comprendre. Rappelez-vous: il n'y a pas de magie ici, des mathématiques simples au cinquième niveau du lycée.

Supposons que nous ayons trois conditions binaires différentes (oui ou non) et une solution binaire en sortie (oui ou non):

Un modèle simple avec trois entrées et une sortie. Ce modèle peut parfaitement fonctionner pour différentes personnes et leur donner des résultats différents, selon la façon dont ils ont formé le réseau neuronal. Mais qu'est-ce qu'un réseau neuronal? Ce ne sont que des blocs séparés - des neurones connectés entre eux. Créons un neurone simple à partir de trois neurones:

Ce que vous voyez entre l'entrée et la sortie, ce sont des neurones. Jusqu'à présent, ils ne sont liés à rien, mais cela reflète également leur caractéristique principale, que tout le monde oublie de dire: ils sont un shnyag complètement abstrait. Autrement dit, les neurones eux-mêmes ne résolvent rien du tout, décide exactement ce que nous allons dessiner ensuite. En attendant, rappelez-vous: les neurones ne font rien du tout, sauf pour rationaliser et simplifier le concept pour les humains. Tirons la partie la plus importante du neurone - la connexion:

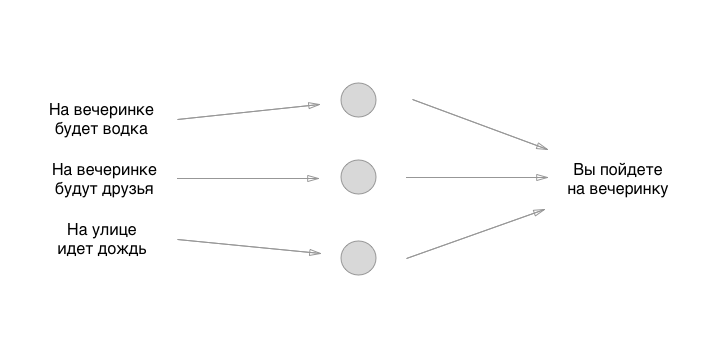
Wow, cela ressemble à quelque chose de super cool. Maintenant, nous allons ajouter de la magie, nous allons en quelque sorte entraîner le neurone avec notre talon gauche, nous tourner en place, rire, jeter du poivre sur l'épaule droite de notre voisin arrière et tout fonctionnera, non? Il s'avère que c'est encore plus facile.

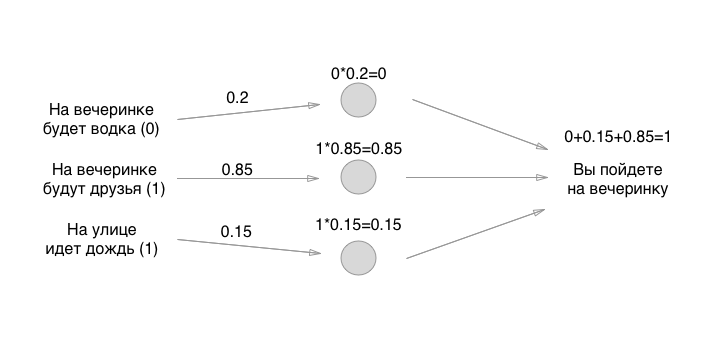
Chaque entrée à gauche a une valeur: 0 ou 1, oui ou non. Ajoutons ces valeurs à l'entrée, supposons qu'il n'y aura pas de vodka à la fête, qu'il y aura des amis, qu'il pleuve:

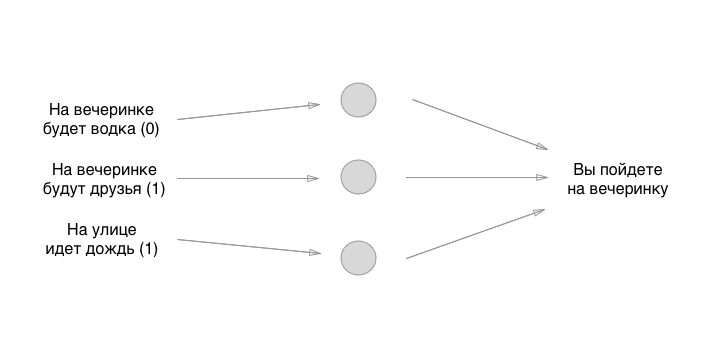
Donc, nous l'avons compris. Que faisons-nous ensuite? Et ici, il y a du plaisir: utilisons la méthode la plus ancienne pour définir l'état initial des neurones - le grand aléatoire:

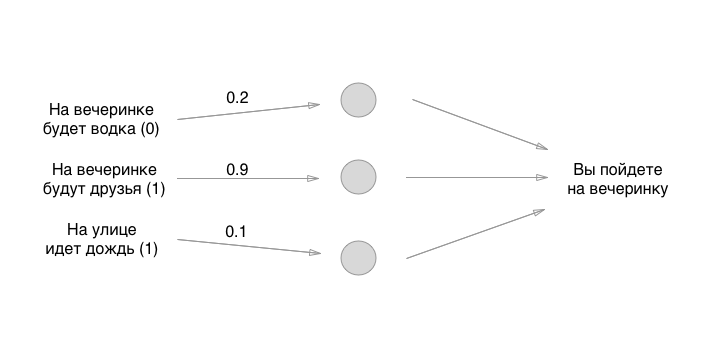
Les nombres que nous fixons sont les poids des obligations. Rappelez-vous que les neurones sont des conneries vides? Ainsi, les communications sont exactement ce qu'est un réseau de neurones. Mais quels sont les poids des obligations? Ce sont les choses par lesquelles nous multiplions les valeurs d'entrée et les stockons temporairement dans des neurones vides. Nous ne le stockons pas réellement, mais pour plus de commodité, nous imaginerons que quelque chose peut être mis dans les neurones:

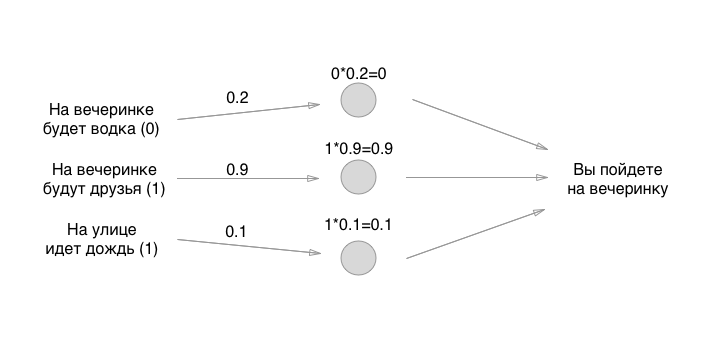
Comment aimez-vous les mathématiques? Pourrait se multiplier? Attendez, la partie la plus difficile vient de commencer! Ensuite, nous ajoutons les valeurs (dans l'une des implémentations perceptron):

Eh bien, c'est tout! Le neurone est créé et vous pouvez l'utiliser pour tous les besoins. Si le montant est supérieur à 0,5, vous devez vous rendre à la fête. S'il est inférieur ou égal, vous n'avez pas besoin d'aller à la fête. Merci de votre attention!

Bien sûr, le modèle ci-dessus a peu d'avantages pratiques, nous devons le former. L'expression effrayante "former des neurones" n'est-ce pas? Pas comme ça. Tout est maladroit et aussi simple que possible: vous prenez des données d'entrée aléatoires (comme nous l'avons fait), exécutez l'entrée à travers ces trois neurones, regardez la réponse - laissez-la être positive (allez à la fête) - et vérifiez si le neurone a correctement prédit la réponse ou non . Si c'est vrai, ne faites rien. Si cela ne va pas, vous déplacez légèrement le poids des neurones (un à la fois ou tous à la fois) dans n'importe quelle direction. Par exemple, comme ceci:

Et encore une fois vous vérifiez: oh, eh bien, encore une fois, il dit d'aller à la fête, quand je ne veux pas y aller! Et vous déplacez à nouveau légèrement les poids (dans la même direction, probablement) un peu, puis passez à nouveau ces données d'entrée à travers les neurones et comparez à nouveau le résultat - et laissez les poids seuls ou déplacez-les à nouveau. Et donc des milliards, des quadrillions de fois, et avec toutes sortes de données d'entrée différentes. Ici, bien sûr, nous n'avons que 8 combinaisons d'entrées, mais il y a différentes tâches (plus à leur sujet ci-dessous).

C'est le principe principal du travail des réseaux de neurones - à la fois la multiplication est nécessaire pour la différenciation, et la compréhension du travail du perceptron est nécessaire pour créer des réseaux convolutifs et des neurones récursifs, et même un jeu exotique.

En conséquence, après avoir formé un neurone sur les décisions prises par une personne, les avoir écrasé des milliards de fois, passer par tous les poids possibles des neurones, vous arriverez enfin à un milieu doré et optimal pour qu'une personne entre trois valeurs initiales - et la machine les exécute formule déjà stable et fonctionnelle avec trois neurones et donne une réponse.

Les trois seules inconnues dans la nôtre étaient les poids des connexions neuronales, et c'est précisément eux que nous avons passés en revue. Par conséquent, je dis que les neurones sont des mannequins qui ne résolvent rien, et les rois d'un banquet sont les poids des connexions.

Ensuite, tout est simple: au lieu d'une couche de neurones, nous en faisons deux et encore une fois nous trions tout selon exactement les mêmes principes, seuls tous les neurones donnent déjà des valeurs à d'autres neurones. Si au début nous n'avions que 3 connexions, maintenant 3 + 9 connexions avec des poids. Et puis trois couches, quatre couches récursives, fixées sur elles-mêmes et le jeu similaire:

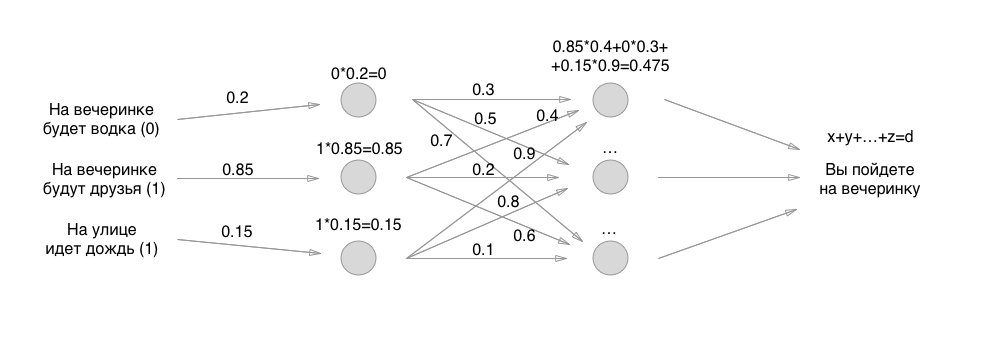
Mais, demandez-moi, disent-ils, quel est le résultat de quelque chose de compliqué dans les neurones? Pourquoi les spécialistes de l'apprentissage automatique sont-ils tant payés? Et la chose est exactement comment implémenter les perceptrons ci-dessus: il y a tellement de nuances différentes que vous êtes tourmenté de lister.

Et si à l'entrée vous avez une photo et que vous devez classer toutes les photos des chiens et des chats? Les images sont en tailles 512x512, chaque pixel est une entrée - alors combien de valeurs allons-nous poursuivre le long des neurones? Il y a des neurones convolutifs pour ça! C'est un tel shnyaga qui prend 9 pixels côte à côte, par exemple, et fait la moyenne de leurs valeurs RVB. Il s'avère, comprime l'image pour un traitement plus rapide. Ou, par exemple, se débarrasse complètement de la couleur rouge dans l'image, car ce n'est pas important (nous ne recherchons, par exemple, que des robes vert-bleu). Ce sont des réseaux convolutionnels - une couche supplémentaire de «neurones» à l'entrée qui traitent l'entrée pour une vue claire et simplifiée pour le réseau.

Vous devez également comprendre combien et dans quelle direction déplacer les poids - pour cela, il existe toutes sortes d'algorithmes simples pour la compréhension, qui prennent en compte l'erreur de la fin - de la droite (du résultat) à la gauche (jusqu'à la première couche de neurones) - l'un des algorithmes est appelé Propagation arrière.

Il existe toutes sortes d'algorithmes sacrément simples pour normaliser les valeurs - de sorte que vous obtenez des nombres non pas de 0 à 500 000, mais de 0 à 1 à la sortie ou au milieu lors de l'ajout - cela simplifie considérablement les calculs et les mathématiques de calcul.

Comme vous pouvez déjà le comprendre, les spécialistes vraiment cool de l'apprentissage automatique connaissent non seulement la plupart des méthodes existantes dans la construction de réseaux de neurones optimisés, mais aussi proposent leurs propres approches, à partir de la compréhension la plus simple mais la plus approfondie des relations de cause à effet entre la façon de construire un perceptron , et pourquoi cela fonctionne, en termes de mathématiques. Ils peuvent non seulement faire fonctionner le neurone, ils peuvent changer l'algorithme ou utiliser un autre algorithme pour continuer à fonctionner rapidement et de manière optimale.

Eh bien, c'est tout - je vous ai donné les bases pour comprendre ce que sont les réseaux de neurones. J'espère aussi vous avoir montré que le diable n'est pas aussi terrible qu'il est peint - tout s'est avéré incroyablement simple, au niveau de la multiplication et de l'addition. Ensuite, je vous conseille de commencer à regarder des tutoriels sur YouTube ou Udemy - il y a des mecs géniaux pour expliquer tout cool.

La prochaine fois, quand ils vous demanderont de l'argent pour un projet d'apprentissage automatique, secouez les mendiants des mendiants avec les grandes lignes du travail des réseaux de neurones - quelles couches, comment elles sont organisées, pourquoi et pourquoi, ici et là, ce n'est pas le cas. Tout cela au niveau d'un maximum de 11 classes sera (il s'agit d'intégrales et de différentiels) - puis cela se produira dans la description une fois, peut-être deux. Bien que le projet ne dispose pas de ce modèle (quelles couches et comment sont situés) - le projet n'a pas de produit, car cette structure est les 2 à 4 premières semaines d'un spécialiste de l'apprentissage automatique.

PS, un exemple d'explication, j'ai impudemment tiré d' une magnifique vidéo sur les réseaux de neurones. Je vous conseille fortement de regarder - merci les gars! les abonnés ont aidé à restaurer le lien vers la vidéo d'origine, un exemple dont j'ai essayé de récupérer la mémoire. Si quelqu'un souhaite savoir comment coder la tâche ci-dessus, je vous invite à regarder cette vidéo ici. Merci beaucoup aux auteurs!