Lors de la résolution des problèmes de transmission de données à travers des lignes représentées par des caractéristiques de fréquence, des transformées de Fourier sont appliquées - le transfert de signaux du domaine temporel vers le domaine fréquentiel et vice versa. L'environnement MATLAB dispose d'un ensemble complet de fonctions pour résoudre de tels problèmes. Dans ce travail, un exemple de calcul dans MATLAB la réaction d'un signal transmis à travers une ligne dont la caractéristique est mesurée à des fréquences qui ne coïncident pas avec la fréquence de transfert de données est analysé. J'espère que cet exemple facilitera la compréhension des fonctionnalités de la technologie de conversion de signal dans l'environnement MATLAB.
Condition de tâche
Il est nécessaire de déterminer la modification de la forme du signal numérique binaire passant par le filtre et la ligne de signal. Le signal est défini par l'amplitude et la vitesse de transmission. Le filtre de second ordre, normalisé à la fréquence de transfert de données, est défini par des constantes de temps. La fonction de transfert de la ligne de signal est représentée par la réponse en fréquence mesurée sous forme complexe.
L'environnement utilisé pour calculer et afficher les données est MATLAB R2015a.
Les relations suivantes publiées sur le site
www.StatEye.org pour la version de la méthode GUI StatEye 3.0 [1, 2, 3] ont été prises comme exemple des données initiales.
Débit bps = 10,3125 Gbit / s. Les constantes de temps du filtre de second ordre normalisé sont les mêmes; leur réciproque est ¾ de la fréquence de transmission des données. La ligne de signal est représentée par une réponse en fréquence. La caractéristique a été mesurée au canal f = 0,006495: 0,0012475: 20 GHz. Le nombre spécifié de points d'échantillonnage de la transformée de Fourier: points = 2 ^ 13.
La figure 1 montre les résultats du transfert, de la séquence et du traitement des données discutés dans cet article. La transition du domaine temporel au domaine fréquentiel et vice versa est effectuée à l'aide de l'algorithme de transformation de Fourier rapide (FFT).
Figure 1. Canal de données. Signal d'entrée iSignal.Tx, signal de sortie du filtre iSignal.Filter_out, ligne de signal de sortie iSignal.Rx. Les caractéristiques montrées dans le diagramme sont discutées ci-dessous.Séquence de calcul
Dans ce travail, les principaux calculs sont effectués dans le domaine fréquentiel. Pour cela, le signal d'origine du domaine temporel est transféré vers le domaine fréquentiel à l'aide de la transformée de Fourier, en multipliant les caractéristiques spectrales du signal, du filtre et de la ligne de signal, le signal de sortie du chemin est trouvé, qui est transféré du domaine fréquentiel au domaine temporel par la transformée de Fourier inverse.
Le taux de transfert de données est deux fois plus élevé que la fréquence à laquelle les données sont transmises. La fréquence maximale de la ligne de signal mesurée max (channel.f) = 20 GHz. À cette fréquence, les données peuvent être transmises à une vitesse de 40 Gbit / s (comme 2 * max (channel.f)).
Le débit de transfert de données maximal, qui ne dépasse pas le débit de transmission maximal sur la ligne de signal de 40 Gbit / s et un débit de transmission multiple bps = 10,3125 Gbit / s, est fmax = 30,9375 Gbit / s, la multiplicité N = 3 (N = fmax / bps). En outre, fmax est utilisé comme fréquence limite pour calculer la réponse du signal en utilisant la transformée de Fourier.
Traduction du signal d'entrée dans le domaine fréquentiel
Discrétion temporelle pour construire le signal d'entrée (bit de données) dans le domaine temporel Ts = 1 / fmax; Ts = 3,232e-11 s. Normalisé par rapport à la durée du signal, l'échelle de temps se compose de 2 ^ 13 points (points), l'échelle comprend le tableau suivant de points temps = bps / Ts. * (1: points). Un signal unique discret à un taux de transmission de bps = 10,3125 Gbit / s et une quantification avec une période Ts = 1 / fmax se compose de trois points dans la plage de 10 à 11 unités de temps normalisé. Un signal d'amplitude unitaire peut être généré n'importe où ailleurs sur la chronologie, mais il est préférable de prendre du recul par rapport aux bords pour voir pleinement l'arrière-plan et le processus de transition du signal de sortie. Un signal d'impulsion (bit de données) construit à l'aide des commandes MATLAB suivantes est illustré à la figure 2.
iSignal.Tx(1:size(time,2)) = 0; t0 = max(find(time<=10)); t1 = max(find(time<11)); iSignal.Tx(t0:t1) = 1.0;
Figure 2. Signal d'impulsion d'entrée iSignal.Tx, bit de données.La traduction du signal iSignal.Tx dans le domaine fréquentiel est effectuée par les fonctions FFT suivantes.
iSignal.shiftedPSD = fft(iSignal.Tx); iSignal.PSD = fftshift(iSignal.shiftedPSD);
La fonction de transformation de Fourier fft construit un spectre symétrique du signal dans les régions de fréquences positives et négatives, dont la fréquence maximale est au centre du spectre (voir figure 3). La fonction fftshift restaure le spectre en décalant vers le centre la fréquence zéro du signal comme indiqué sur la figure 4.
La résolution de la fréquence du spectre est fs = fmax / points; Les fréquences du spectre varient de -fmax / 2 à fmax / 2-fs et sont égales à f = -fmax / 2: fs: fmax / 2-fs;
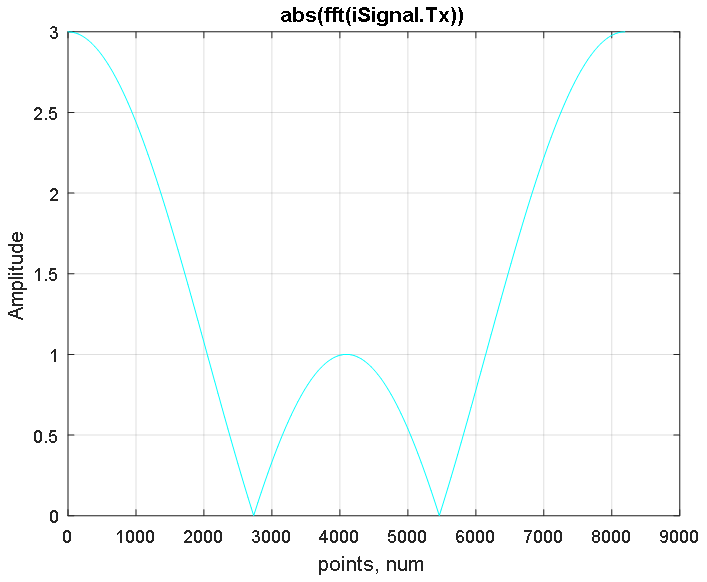Figure 3. Réponse en amplitude du spectre décalé du signal iSignal.Tx obtenu en utilisant la FFT.
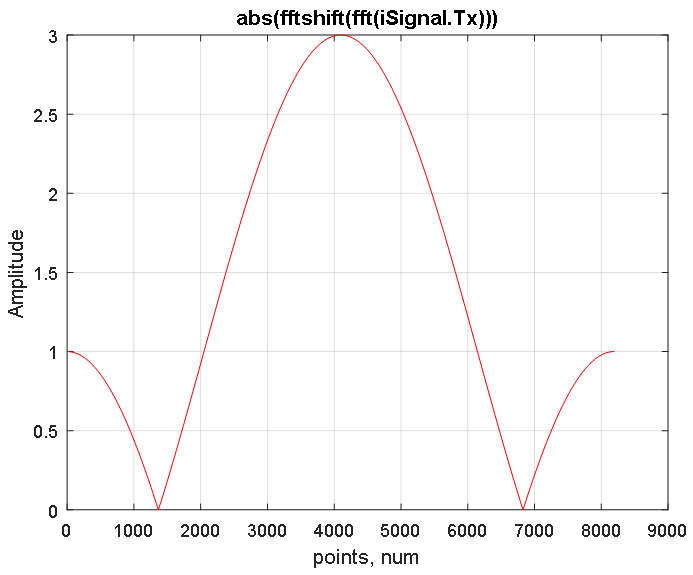Figure 4. Réponse en amplitude du spectre reconstruit du signal iSignal.Tx représenté sur la figure 3. 2 ^ 13 échantillons sont présentés. Le compte moyen à 4097 correspond à une fréquence nulle. Les fréquences négatives sont situées sur le côté gauche (de 1 à 4096 points), et la région des fréquences positives sur le côté droit (de 4098 à 8192 points).Fonction de transfert du filtre passe-bas normalisé
Dans cet exemple, la fonction de transfert du filtre de second ordre a la forme
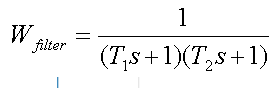
où T1 et T2 sont des constantes de temps de filtrage. Les fréquences 1 / T1 sont égales et 1 / T2 sont fixées par rapport à la fréquence à laquelle les données sont transmises: 1 / T1 = 1 / T2 = 0,75 * bps (bps = 10,3125 Gbit / s).
Bande passante de filtre normalisée
f_nrm =fmax/bps/points.*(-points/2:points/2-1).
Opératrice
s = f_nrm .* j;
La caractéristique amplitude-phase du filtre normalisé pour les fréquences positives et négatives normalisées par rapport à la fréquence de transmission du signal est représentée sur la figure 5. La caractéristique logarithmique amplitude-fréquence du filtre est représentée sur la figure 6.
Figure 5. La caractéristique amplitude-phase d'un filtre normalisé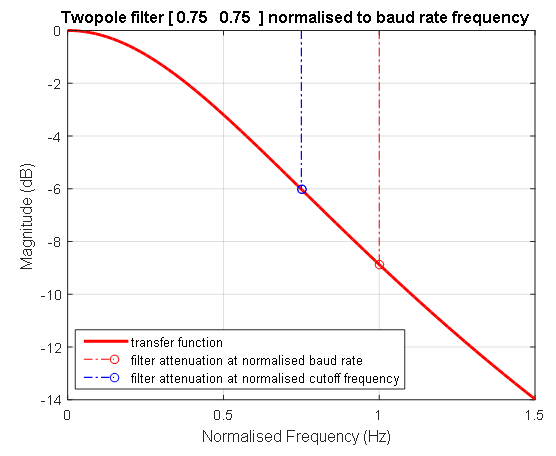
Figure 6. Réponse en fréquence amplitude-phase logarithmique d'un filtre normalisé. La ligne pointillée bleue montre la position de la fréquence du filtre avec une valeur de 0,75 de la fréquence à laquelle les données sont transmises. A cette fréquence (1 / T1 = 1 / T2), le coefficient de transmission du filtre de second ordre est de -6 décibels. La ligne pointillée rouge indique la fréquence unitaire à laquelle les données sont transmises.Traduction des résultats de mesure de ligne de signal en type de fonction de transfert
La caractéristique d'amplitude-phase mesurée de la ligne de signal comprend 1599 échantillons dans la bande jusqu'à 20 GHz avec un pas fixe de 12,475 MHz. Il contient les valeurs de fréquence suivantes: channel.f = 0,006495: 0,0012475: 20 GHz. Initialement, la ligne de signal était représentée par une caractéristique à quatre bornes. Cette caractéristique a été transformée et est utilisée dans l'exemple comme une fonction complexe unidimensionnelle.
Les fréquences caractéristiques de la ligne de signal obtenues à la suite de la mesure ne coïncident pas avec les fréquences du spectre du signal d'entrée qui sont des multiples de la fréquence de transmission des données. De plus, le spectre de ligne de signal ne contient que des fréquences positives et ne contient pas de fréquences dans la région zéro. Le spectre du signal d'entrée contient des fréquences positives, nulles et négatives.
Pour convertir les caractéristiques de la ligne de signal en une fonction de transfert - une caractéristique dont les fréquences coïncident avec les fréquences du spectre du signal d'entrée, les étapes suivantes sont prises.
1. Le calcul de l'amplitude des caractéristiques de la ligne à fréquence nulle en l'extrapolant. Pour cela, à partir de dix points de la caractéristique d'amplitude les plus proches de la fréquence zéro, on trouve les coefficients d'un polynôme linéaire qui se rapprochent de la caractéristique d'amplitude:
[a] = polyfit(channel.f(1:10), channel.abs(1:10), 1);
Le deuxième coefficient polynomial trouvé est égal à l'amplitude de la caractéristique à fréquence nulle:
channel.dc = a(2);
2. La réponse de phase à fréquence nulle est prise égale à zéro.
channel.dcPhase = 0.00;
3. Le recalcul des caractéristiques d'amplitude channel.abs et phase channel.phase de la ligne de signal avec des valeurs à fréquence nulle est effectué sur la fréquence du spectre du signal d'entrée (f = -fmax / 2: fmax / points: fmax / 2-fmax / points) avec extrapolation des caractéristiques à zone de fréquences nulles et négatives:
ichannel.abs = interp1([0 channel.f], [channel.dc channel.abs], abs(f), 'linear', 'extrap'); ichannel.phase = interp1([0 channel.f], [channel.dcPhase unwrap(channel.phase)], abs(f), 'linear', 'extrap'); ichannel.s = ichannel.abs .* exp(+j.*ichannel.phase); ichannel.tf = real(ichannel.s) + j*imag(ichannel.s) .* sign(f);
La fonction de transfert obtenue - la réponse en fréquence amplitude-phase du canal dans la région des basses fréquences est illustrée à la figure 7. Les caractéristiques amplitude-fréquence de la ligne de signal mesurée et la fonction de transfert calculée dans les gammes de fréquences complètes sont illustrées à la figure 8. Les mêmes caractéristiques dans l'espace des phases sont illustrées à la figure 9.
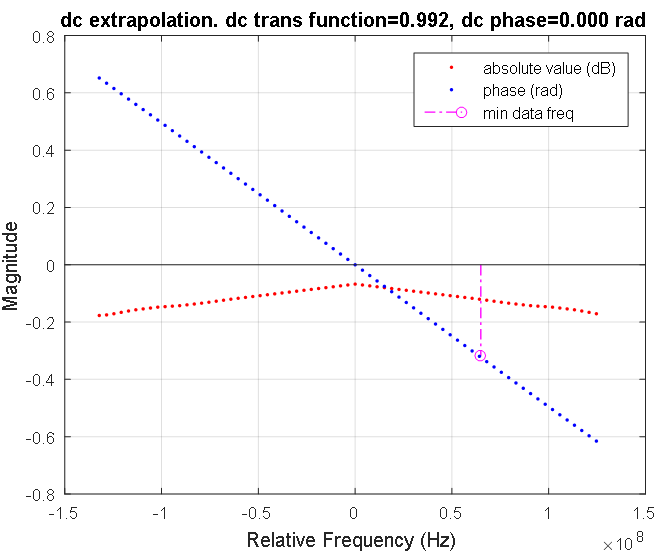Figure 7. La fonction de transfert de la ligne de signal dans la région des basses fréquences. Les points rouges et bleus indiquent respectivement les caractéristiques discrètes d'amplitude et de phase. La réponse en amplitude est indiquée en décibels, la phase en radians. La ligne rose marque la fréquence la plus basse de la caractéristique mesurée de la ligne de signal. Le coefficient de transmission à fréquence nulle est de 0,992.
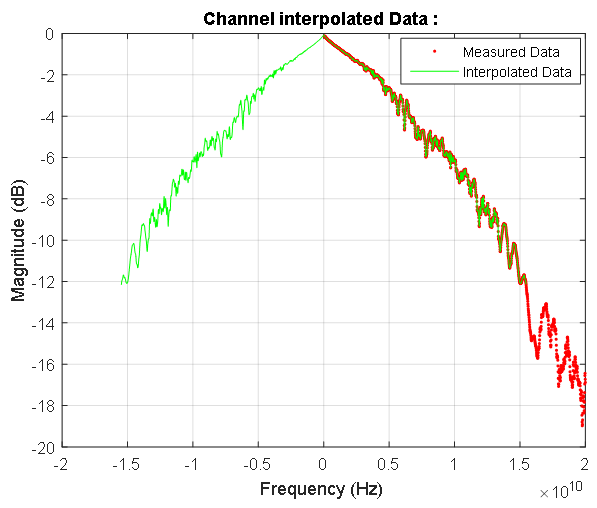Figure 8. Réponse en fréquence de la ligne de signal. Les points bleus indiquent les données complexes de la ligne mesurée. La dépendance symétrique calculée du gain de la ligne de signal aux fréquences du spectre du signal d'entrée est surlignée en rouge. Dans la région de fréquence nulle, cette caractéristique est illustrée à la figure 7.
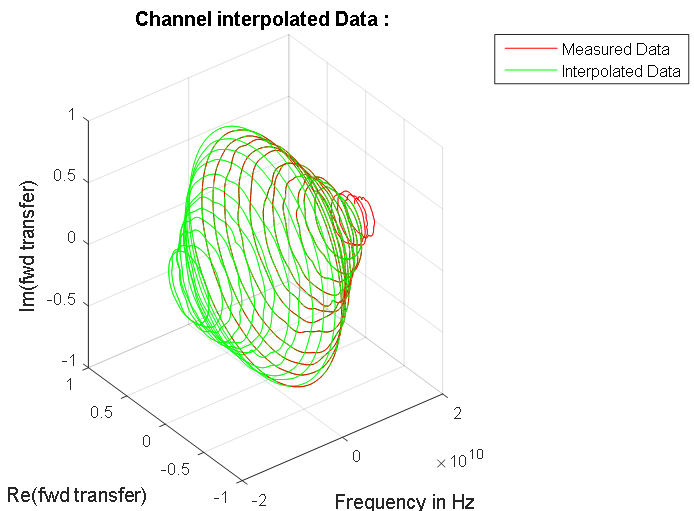Figure 9. Caractéristiques de fréquence amplitude-phase de la ligne de données mesurée et son spectre normalisé.Calcul de la réponse du signal
La réponse (réponse à l'effet d'entrée) dans le domaine fréquentiel est obtenue en multipliant le spectre du signal par le produit des fonctions de transfert des éléments qui relient la réaction au signal d'entrée. Dans notre cas, le signal passe à travers le filtre et la ligne de signal.
La transformée de Fourier inverse ifft est utilisée pour transférer le signal du domaine fréquentiel vers le domaine temporel.
La sortie du filtre dans le domaine temporel iSignal.Filter_out est calculée comme suit:
TransFunction.PSD = iSignal.PSD .* Filter.PSD_Tx; TransFunction.shiftedPSD = ifftshift(TransFunction.PSD); iSignal.Filter_out = real(ifft(TransFunction.shiftedPSD));
Le signal de sortie de la ligne iSignal.Rx est égal au produit du spectre du signal d'entrée et des fonctions de transfert du filtre et de la ligne de signal avec le transfert ultérieur du signal reçu du domaine fréquentiel vers le domaine temporel.
TransFunction.PSD = TransFunction.PSD .* ichannel.tf; TransFunction.shiftedPSD = ifftshift(TransFunction.PSD); iSignal.Rx = real(ifft(TransFunction.shiftedPSD));
La réponse du filtre à l'impulsion idéale d'entrée et la réponse du canal sont illustrées à la figure 10.
Figure 10. Sortie du filtre (graphique rouge) et sortie de la ligne de données (graphique vert). Signal d'entrée du filtre - une seule impulsion est représentée sur la figure 2. L'entrée de ligne de signal est le signal de sortie du filtre.Application. Code m MATLAB d'occasion
Liste bibliographique
1. IEEE802.3ap. 10.3125Gbps NRZ Simulation Results Using "StatEye" and "Signal to Interference Model" on Cascaded Channel Components. Shannon Sawyer et Charles Moore / Agilent Technologies. 24 janvier 2005
www.ieee802.org/3/ap/public/jan05/sawyer_01_0105.pdf2. Qu'est-ce que StatEye. Groupe de travail IEEE 803.3ap. 16 septembre 2004
www.ieee802.org/3/ap/public/signal_adhoc/ghiasi_01_0904.pdf3. Accord Stat Eye / IBM. Steve Anderson. Xilinx, Inc.
www.ieee802.org/3/ap/public/nov04/anderson_01_1104.pdf