Formation sur la durabilité GAN

L'idée du GAN a été publiée pour la première fois par Jan Goodfellow Generative Adversarial Nets, Goodfellow et al 2014 , après quoi les GAN sont l'un des meilleurs modèles génératifs.

Comme pour tout autre modèle génératif, la tâche GAN consiste à construire un modèle de données et, plus précisément, à apprendre à générer des échantillons à partir d'une distribution aussi proche que possible de la distribution de données (il existe généralement un ensemble de données de taille limitée dans lequel nous voulons modéliser la distribution de données).

Les GAN présentent un grand nombre d'avantages, mais ils présentent un inconvénient important: ils sont très difficiles à former.

Récemment, un certain nombre d'ouvrages sur la durabilité du GAN ont été publiés:

• L'optimisation du gradient GAN de descente est localement stable, Vaishnavh Nagarajan, J.Zico Kolter, 2017
• The Numerics of GANs, Lars Mescheder et al, 2017

Inspiré par leurs idées, j'ai fait quelques recherches.

J'ai essayé de rendre le texte aussi simple que possible et, si possible, d'utiliser uniquement les mathématiques les plus simples. Malheureusement, pour justifier pourquoi nous pouvons considérer les propriétés des champs vectoriels bidimensionnels, nous devons creuser un peu dans le sens du calcul des variations. Mais si quelqu'un ne connaît pas ces termes, vous pouvez immédiatement procéder en toute sécurité à la prise en compte de champs vectoriels bidimensionnels pour différents types de GAN.

Nous allons maintenant essayer de regarder sous le capot de la procédure de formation et de comprendre ce qui s'y passe.

GAN, le principal problème

Les GAN sont constitués de deux réseaux de neurones: un discriminateur et un générateur. Générateur - vous permet d'échantillonner à partir d'une distribution (généralement appelée distribution du générateur). Le discriminateur reçoit des échantillons d'entrée de l'ensemble de données et du générateur d'origine et apprend à prédire d'où vient cet échantillon (ensemble de données ou générateur).

Régime GAN:



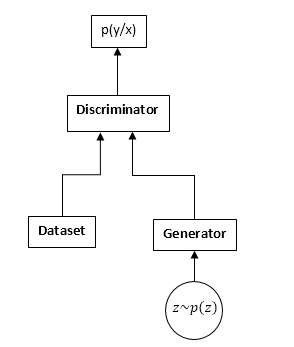
Le processus de formation du GAN est le suivant:

1. Nous prenons n échantillons de l'ensemble de données et m échantillons du générateur.
2. Nous fixons les poids du générateur et mettons à jour les paramètres du discriminateur. Il s'agit d'une tâche de classification courante. Nous n'avons tout simplement pas besoin de former le discriminateur jusqu'à la convergence. Et encore plus souvent, il interfère également.
3. Nous fixons les poids du discriminateur et mettons à jour les poids du générateur, de sorte que le discriminateur commence à penser que nos échantillons proviennent de l'ensemble de données et non du générateur.
4. Nous répétons 1-3, jusqu'à ce que le discriminateur et le générateur s'équilibrent (c'est-à-dire qu'aucun des autres ne peut «tromper» l'autre).

Nous n'examinerons pas en détail le processus d'apprentissage du GAN. Sur Internet, et sur l'hubr en particulier, il existe de nombreux articles expliquant ce processus en détail.

Nous serons intéressés par quelque chose de complètement différent. À savoir, en raison du fait que nous sommes en concurrence avec deux réseaux de neurones, la tâche cesse d'être une recherche d'un minimum (maximum), mais se transforme dans des cas particuliers en recherche d'un point de selle (c'est-à-dire qu'aux étapes 2 et 3, nous essayons la même fonction maximiser par les paramètres du discriminateur et minimiser par les paramètres du générateur), et dans les étapes plus générales 2 et 3, nous pouvons optimiser des fonctions complètement différentes. De toute évidence, le problème minimax est un cas particulier d'optimisation de différentes fonctionnelles - une fonction est prise avec des signes différents.

Regardons cela dans les formules. Nous supposons que pd (x) est la distribution à partir de laquelle l'ensemble de données est échantillonné, pg (x) est la distribution du générateur, D (x) est la sortie du discriminateur.

Lors de la formation d'un discriminateur, nous maximisons souvent une telle fonctionnalité:

$$

$$J \ = \ \ int {p_d (x) log (D (x)) dx \ + \ \ int {p_g (x) log (1 \ - \ D (x)) dx}}$$

Vecteur de dégradés:

$$

$$v = \ \ nabla_ \ theta J \ = \ int {\ frac {p_d (x)} {D (x)} \ nabla_ \ theta D (x) \ dx \ + \ \ int {\ frac {p_g (x )} {1 \ - \ D (x)} \ nabla_ \ theta D (x) dx}}$$

Lors de la formation du générateur, nous maximisons:

$$

$$I \ = \ - \ int {p_g (x) log (1 \ - \ D (x)) dx}$$

Le vecteur de dégradés dans ce cas:

$$

$$u \ = \ \ nabla_ \ varphi I \ = \ - \ int {{\ nabla_ \ varphi p} _g (x) log (1 \ - \ D (x)) dx}$$

Dans le futur, nous verrons que les fonctionnelles peuvent être remplacées respectivement par:

$$

$$J \ = \ \ int {p_d (x) f_1 (D (x)) dx \ + \ \ int {p_g (x) f_2 (D (x)) dx}}$$

$$

$$I \ = \ \ int {p_g (x) f_3 (D (x)) dx}$$

O Where $$$f_1, f_2, f_3$ sont sélectionnés selon certaines règles. Soit dit en passant, Ian Goodfellow utilise dans son article original $$$f_1 et f_2$ comme lors de la formation d'un discriminateur régulier, et $$$f_3$ choisit de manière à améliorer les gradients au stade initial de la formation:

$$

$$f_1 \ left (x \ right) = log \ left (x \ right), \ f_2 \ left (x \ right) = log \ left (1 \ - \ x \ right), f_3 \ left (x \ right) = log \ gauche (x \ droite)$$

À première vue, la tâche semble être très similaire à la tâche habituelle d'apprendre avec une descente en pente (ascension). Pourquoi, alors, tous ceux qui ont suivi la formation du GAN ont-ils convenu que c'était si dur?

La réponse réside dans la structure du champ vectoriel, que nous utilisons pour mettre à jour les paramètres des réseaux de neurones. Dans le cas du problème de classification habituel, nous utilisons uniquement le vecteur de gradient, c'est-à-dire que le champ est potentiel (la fonction optimisée elle-même est le potentiel de ce champ vectoriel). Et les champs vectoriels potentiels ont des propriétés remarquables, dont l'absence de courbes fermées. Autrement dit, il est impossible de tourner en rond dans ce domaine. Mais lors de la formation du GAN, malgré le fait que les champs vectoriels pour le générateur et le discriminateur sont séparément potentiels (les mêmes sont des gradients), le champ vectoriel total ne sera pas potentiel. Et cela signifie que dans ce domaine, il peut y avoir des courbes fermées, c'est-à-dire que nous pouvons marcher en rond. Et c'est très, très mauvais.

La question se pose: pourquoi, tout de même, nous parvenons à former le GAN avec succès, peut-être que le domaine est encore irrotational (potentiel)? Et si oui, alors pourquoi est-ce si compliqué?
Je vais continuer, malheureusement, le champ n'est pas potentiel, mais il a un certain nombre de bonnes propriétés. Malheureusement, le domaine est également très sensible à la paramétrisation des réseaux de neurones (choix des fonctions d'activation, utilisation de DropOut, BatchNormalization, etc.). Mais tout d'abord.

Champ GAN «dégradé»

Nous considérerons les fonctionnalités d'apprentissage du GAN sous la forme la plus générale:

$$

$$J \ = \ \ int {p_d (x) f_1 (D (x)) dx \ + \ \ int {p_g (x) f_2 (D (x)) dx}}$$

$$

$$I \ = \ \ int {p_g (x) f_3 (D (x)) dx}$$

Nous devons optimiser les deux fonctionnalités en même temps. En supposant que D (x) et pg (x) sont des fonctions absolument flexibles, c'est-à-dire nous pouvons prendre n'importe quel nombre à tout moment, indépendamment d'autres points. C'est un fait bien connu du calcul des variations - vous devez changer la fonction dans le sens de la dérivée variationnelle de cette fonctionnelle (en général, un analogue complet de l'augmentation du gradient).

Nous écrivons la dérivée variationnelle:

$$

$$\ frac {\ partial J} {\ partial D (x)} = p_d (x) f_1 '(D (x)) \ + \ p_g (x) f_2' (D (x))$$

$$

$$\ frac {\ partial I} {\ partial p_g (x)} = f_3 (D (x))$$

Nous ne considérerons que le premier fonctionnel (pour le discriminateur), pour le second tout sera le même.

Mais considérant qu'en fait on ne peut changer la fonction que dans l'ensemble des fonctions représentables par notre réseau neuronal, on écrira:

$$$$ afficher $$ ∆D (x) = \ frac {\ partiel D (x)} {\ partiel θ_j} Δθ_j $$ afficher $$

changements dans les paramètres du réseau, en général, la descente (montée) habituelle du gradient:

$$$$ afficher $$ ∆θj = \ frac {\ partiel J} {\ partiel θ_j} μ $$ afficher $$

µ est le taux d'apprentissage. Eh bien, la dérivée par rapport aux paramètres du réseau:

$$

$$\ frac {\ partial J} {\ partial \ theta_j} = \ int {\ frac {\ partial J} {\ partial D (y)} \ frac {\ partial D (y)} {\ partial \ theta_j} dy }$$

Et maintenant, nous mettons tout cela ensemble:

$$

$$∆D (x) = \ sum_ {j} {\ frac {\ partial D (x)} {\ partial \ theta_j} \ int {\ frac {\ partial J} {\ partial D (y)} \ frac { \ partial D (y)} {\ partial \ theta_j} dy} \ mu \ = \ mu \ int \ frac {\ partial J} {\ partial D (y)}} \ sum_ {j} {\ frac {\ partial D (x)} {\ partial \ theta_j} \ frac {\ partial D (x)} {\ partial \ theta_j} dy \ = \} \ mu \ int {\ frac {\ partial J} {\ partial D (y )} K_ \ thêta (x, y) dy}$$

Où: $$$K_ \ theta (x, y) \ = \ sum_ {j} {\ frac {\ partial D (x)} {\ partial \ theta_j} \ frac {\ partial D (x)} {\ partial \ theta_j} \ }$

Je n'ai jamais vu cette fonctionnalité dans la littérature sur l'apprentissage automatique, je l'appellerai donc le noyau paramétrique du système.

Eh bien, ou si nous passons à des pas continus dans le temps (des équations de différence aux équations différentielles), nous obtenons:

$$

$$\ frac {d} {dt} D (x) \ = \ \ int {\ frac {\ partial J} {\ partial D (y)} K_ \ theta (x, y) dy}$$

Cette équation montre la relation interne du champ d'origine (point par point pour le discriminateur) et la paramétrisation du réseau neuronal. Nous obtenons une équation complètement similaire pour le générateur.

Étant donné que K (x, y) (le noyau paramétrique) est une fonction définie positive (eh bien, comment peut-il être représenté comme un produit scalaire de gradients aux points correspondants), nous pouvons conclure que tout changement dans les fonctions entraînées (discriminateur et générateur) appartient à l'espace de Hilbert généré par le noyau, c'est-à-dire K (x, y). Je me demande s'il est possible d'obtenir des résultats significatifs ici. Mais nous ne regarderons pas encore dans cette direction, mais nous regarderons dans l'autre.

Comme vous pouvez le voir, la stabilité du GAN est déterminée par deux composantes: les dérivées variationnelles des fonctionnelles et la paramétrisation du réseau neuronal. Notre tâche est de voir comment ce champ se comporte de manière ponctuelle, c'est-à-dire si notre réseau peut représenter absolument n'importe quelle fonction. La tâche se transforme en une analyse d'un champ vectoriel bidimensionnel. Et cela, je pense, est en notre pouvoir.

Durabilité

Nous considérons donc le champ vectoriel suivant:

$$

$$\ frac {d} {dt} D (x) = \ \ frac {\ partial J} {\ partial D (x)}$$

$$

$$\ frac {d} {dt} p_g (x) = \ \ frac {\ partial I} {\ partial p_g (x)}$$

De toute évidence, ces équations ne peuvent être considérées que pour un seul point x, en tenant compte de la façon dont nos dérivées variationnelles ressemblent:

$$

$$\ frac {d} {dt} D = \ p_df_1 ^ \ prime (D) \ + \ p_gf_2 ^ \ prime (D)$$

$$

$$\ frac {d} {dt} p_g \ = \ f_3 (D)$$

La première exigence pour ce système d'équations est que les côtés droit doivent aller à 0 lorsque:
$$$p_d = p_g$

Sinon, nous essaierons de former le modèle, qui ne convergera évidemment pas vers la bonne solution. C'est-à-dire D doit être une solution à l'équation suivante:

$$

$$f_1 ^ \ prime (D) \ + \ f_2 ^ \ prime (D) \ = \ 0$$

Nous désignons cette solution comme $$$D0$ .

Étant donné que pg (x) est la densité de probabilité du côté droit, nous pouvons ajouter n'importe quel nombre sans violer les dérivées. Afin de fournir 0 du côté droit au point souhaité, soustrayez la valeur en t. $$$D0$ (cela doit être fait si nous voulons considérer pg point par point - la transition d'un champ paramétré par des densités de probabilité à des champs libres).

En conséquence, nous obtenons le champ suivant:

$$

$$\ frac {d} {dt} D = \ p_df_1 ^ \ prime (D) \ + \ p_gf_2 ^ \ prime (D)$$

$$

$$\ frac {d} {dt} p_g \ = \ f_3 (D) \ - \ f (D0)$$

Désormais, nous étudierons les points de repos et la stabilité des champs de ce type.
Nous pouvons étudier deux types de stabilité: locale (au voisinage du point de repos) et globale (en utilisant la méthode de la fonction de Lyapunov).

Pour étudier la stabilité locale, il est nécessaire de calculer la matrice de Jacobi du champ.
Pour que le champ soit localement «stable», il faut que les valeurs propres aient une partie réelle négative.

Différents types de GAN

1. Classic GAN

   
   
   Dans le GAN classique, nous utilisons la perte de journal régulière:
   

   $$

   $$J \ = \ \ int {p_d (x) log (D (x)) dx \ + \ \ int {p_g (x) log (1 \ - \ D (x)) dx}}$$
   
   Pour la formation du discriminateur, il est nécessaire de le maximiser; pour le générateur, de le minimiser. Dans ce cas, le champ ressemblera à ceci:
   

   $$

   $$\ frac {d} {dt} D = \ \ frac {p_d} {D} \ - \ \ frac {p_g} {1-D}$$
   
   

   $$

   $$\ frac {d} {dt} p_g \ = \ -log (1-D) \ + \ log (\ frac {1} {2})$$
   
   Voyons comment les paramètres (pg et D) vont évoluer dans ce domaine. Pour ce faire, utilisez ce simple script Python:
   
   
   Script

   def get_v(d, pg, pd): vd = pd/d - pg/(1.-d) vpg = -np.log(1.-d) + np.log(0.5) return vd, vpg d = 0.75 pg = 0.9 pd = 0.2 d_hist = [] pg_hist = [] lr = 1e-3 n_iter = 100000 for i in range(n_iter): d_hist.append(d) pg_hist.append(pg) vd, vpg = get_v(d, pg, pd) d = d + lr*vd pg = pg + lr*vpg plt.plot(d_hist, pg_hist, '-') plt.show() 

   
   
   
   Pour le point de départ $$$p_g = 0,9, D = 0,25$ cela ressemblera à ceci:
   
   
   
   Le point de repos d'un tel champ sera: pg = pd et D = 0,5
   
   On peut facilement vérifier que les parties réelles des valeurs propres de la matrice de Jacobi sont négatives, c'est-à-dire que le champ est localement stable.
   Nous ne traiterons pas de la preuve de la durabilité mondiale. Mais si c'est très intéressant, vous pouvez jouer avec le script Python et vous assurer que le champ est stable pour toutes les valeurs initiales valides.

2. Modification par Jan Goodfellow

   
   Nous avons déjà expliqué ci-dessus que Ian Goodfellow dans l'article d'origine utilisait une version légèrement modifiée de GAN. Pour sa version, les fonctions étaient les suivantes:
   

   $$

   $$f_1 \ left (x \ right) = log \ left (x \ right), \ f_2 \ left (x \ right) = log \ left (1 \ - \ x \ right), f_3 \ left (x \ right) = log \ gauche (x \ droite)$$
   
   Le champ ressemblera à ceci:
   

   $$

   $$\ frac {d} {dt} D = \ \ frac {p_d} {D} \ - \ \ frac {p_g} {1-D}$$
   
   

   $$

   $$\ frac {d} {dt} p_g \ = \ log (D) \ - \ log (\ frac {1} {2})$$
   
   Le script python sera le même, seule la fonction de champ est différente:
   
   
   Script

    def get_v(d, pg, pd): vd = pd/d - pg/(1.-d) vpg = np.log(d) - np.log(0.5) return vd, vpg d = 0.75 pg = 0.9 pd = 0.2 d_hist = [] pg_hist = [] lr = 1e-3 n_iter = 100000 for i in range(n_iter): d_hist.append(d) pg_hist.append(pg) vd, vpg = get_v(d, pg, pd) d = d + lr*vd pg = pg + lr*vpg plt.plot(d_hist, pg_hist, '-') plt.show() 

   
   
   
   Et avec les mêmes données initiales, l'image ressemble à ceci:
   
   
   
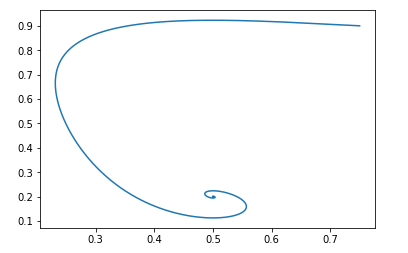
   Et encore une fois, il est facile de vérifier que le champ sera localement stable.
   Autrement dit, du point de vue de la convergence, une telle modification n'altère pas les propriétés du GAN, mais elle a ses avantages en termes d'entraînement des réseaux de neurones.

3. Wasserstein gan

   
   Regardons une autre vue populaire du GAN. La fonctionnalité optimisée ressemble à ceci:
   

   $$

   $$J \ = \ \ int {p_d (x) D (x) dx \ - \} \ int {p_g (x) D (x) dx}$$
   
   Où D appartient à la classe des fonctions 1-Lipschitz par rapport à x.
   Nous voulons le maximiser de D et le minimiser de pg.
   
   De toute évidence, dans ce cas: $$$f_1 \ left (x \ right) = x, \ f_2 \ left (x \ right) = - x, \ f_3 \ left (x \ right) = x$
   
   Et le champ ressemblera à ceci:
   

   $$

   $$\ frac {d} {dt} D = \ p_d \ - {\ p} _g \ $$
   
   

   $$

   $$\ frac {d} {dt} p_g \ = \ D$$
   
   Dans ce domaine, un cercle avec un centre en un point est facilement deviné. $$$p_g = p_d, D = 0$ .
   Autrement dit, si nous suivons ce domaine, nous tournerons toujours en rond.
   
   Voici un exemple de trajectoire dans un tel domaine:
   
   
   
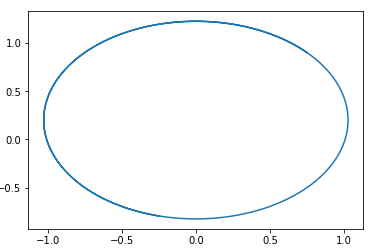
   La question est, alors pourquoi se révèle-t-il former ce type de GAN? La réponse est très simple - cette analyse ne prend pas en compte le fait de la propriété 1-Lipschitz de D. Autrement dit, nous ne pouvons pas prendre de fonctions arbitraires. Soit dit en passant, cela est en bon accord avec les résultats des auteurs ... de l'article. Pour éviter de marcher en cercle, ils recommandent de former le discriminateur à converger: Wasserstein GAN

4. Nouvelles options GAN

   
   Sélection des fonctionnalités $$$f_1, f_2 et f_3$ Vous pouvez créer différentes options GAN. La principale exigence de ces fonctions est d'assurer la présence d'un point de repos «correct» et la stabilité de ce point (de préférence global, mais au moins local). Je donne au lecteur l'occasion de dériver les restrictions sur les fonctions f1, f2 et f3, nécessaires à la stabilité locale. C'est facile - il suffit de considérer l'équation quadratique pour les valeurs propres de la matrice de Jacobi.
   
   Je vais donner un exemple d'un tel GAN:
   

   $$

   $$f_1 (x) \ = \ -0,5x ^ 2, \ f_2 (x) \ = \ x, \ f_3 (x) \ = \ -x$$
   
   Encore une fois, je suggère au lecteur de construire lui-même le champ de ce GAN et de prouver sa stabilité. (Soit dit en passant, c'est l'un des rares domaines pour lesquels la preuve de la stabilité globale est élémentaire - il suffit de sélectionner la fonction Lyapunov, la distance jusqu'au point de repos). Tenez simplement compte du fait que le point de repos est D = 1.

Conclusion et recherches complémentaires

Il ressort de l'analyse ci-dessus que tous les GAN classiques (à l'exception du Wassertein GAN, qui a ses propres méthodes pour améliorer la stabilité) ont de «bons» champs. C'est-à-dire la suite de ces champs a un point de repos unique auquel la distribution du générateur est égale à la distribution des données.

Pourquoi, alors, former le GAN est une tâche si difficile. La réponse est simple - paramétrage des réseaux de neurones. Avec un "mauvais" paramétrage, on peut aussi se promener en rond. Par exemple, mes expériences montrent que, par exemple, l'utilisation de BatchNormalization dans l'un des réseaux transforme immédiatement le champ en champ fermé. Et l'activation Relu fonctionne mieux.

Malheureusement, pour le moment, il n'y a pas une seule façon de vérifier théoriquement quels éléments du réseau neuronal comment changer le champ. Il me semblera prospectif d'étudier les propriétés du noyau paramétrique du système - $$$K_ \ thêta (x, y)$ .

Je voulais également parler des moyens de régulariser les champs GAN et les examiner sous l'angle des champs bidimensionnels. Considérez les algorithmes d'apprentissage par renforcement dans cette perspective. Et bien plus. Mais malheureusement, l'article s'est avéré être de toute façon trop gros, alors en savoir plus à ce sujet une autre fois.