Cours MIT "Sécurité des systèmes informatiques". Conférence 2: «Contrôle des attaques de pirates», partie 3

Institut de technologie du Massachusetts. Cours magistral # 6.858. "Sécurité des systèmes informatiques." Nikolai Zeldovich, James Mickens. 2014 année

Computer Systems Security est un cours sur le développement et la mise en œuvre de systèmes informatiques sécurisés. Les conférences couvrent les modèles de menace, les attaques qui compromettent la sécurité et les techniques de sécurité basées sur des travaux scientifiques récents. Les sujets incluent la sécurité du système d'exploitation (OS), les fonctionnalités, la gestion du flux d'informations, la sécurité des langues, les protocoles réseau, la sécurité matérielle et la sécurité des applications Web.

Cours 1: «Introduction: modèles de menace» Partie 1 / Partie 2 / Partie 3
Conférence 2: «Contrôle des attaques de pirates» Partie 1 / Partie 2 / Partie 3

Pouvez-vous me dire quel est le manque d'une approche de sécurité qui utilise une page de garde ?

Public: cela prend plus de temps!

Professeur: exactement! Imaginez donc que ce tas soit très, très petit, mais j'ai sélectionné une page entière pour m'assurer que cette toute petite chose n'était pas attaquée par un pointeur. Il s'agit d'un processus très exigeant sur le plan spatial, et les gens ne déploient pas réellement quelque chose comme ça dans un environnement de travail. Cela peut être utile pour tester des "bugs", mais vous ne le feriez jamais pour un vrai programme. Je pense que vous comprenez maintenant ce qu'est un débogueur de mémoire de clôture électrique .

Public: Pourquoi la page de garde devrait-elle être si grande?

Professeur: La raison en est qu'ils dépendent généralement du matériel, comme la protection au niveau des pages, pour déterminer les tailles de page. Pour la plupart des ordinateurs, 2 pages de 4 Ko sont allouées pour chaque tampon alloué, pour un total de 8 Ko. Le tas étant constitué d'objets, une page distincte est allouée pour chaque fonction malloc . Dans certains modes, ce débogueur ne renvoie pas l'espace réservé au programme, donc la clôture électrique est très vorace en termes de mémoire et ne doit pas être compilée avec du code de travail.



Une autre approche de sécurité qui mérite d'être examinée s'appelle les pointeurs Fat , ou «pointeurs épais». Dans ce cas, le terme «épais» signifie qu'une grande quantité de données est attachée au pointeur. Dans ce cas, l'idée est que nous voulons changer la représentation même du pointeur afin d'inclure des informations sur les limites dans sa composition.

Un pointeur 32 bits standard se compose de 32 bits et des adresses se trouvent à l'intérieur. Si nous considérons le "pointeur épais", il se compose de 3 parties. La première partie est une base de 4 octets, à laquelle est également attachée une fin de 4 octets. Dans la première partie, l'objet commence, dans la seconde il se termine, et dans la troisième, également de 4 octets, l'adresse cur est incluse. Et à l'intérieur de ces frontières communes se trouve un pointeur.



Ainsi, lorsque le compilateur génère un code d'accès pour ce "pointeur épais", il met à jour le contenu de la dernière partie de l' adresse cur et vérifie simultanément le contenu des deux premières parties pour s'assurer que rien de mauvais ne s'est produit avec le pointeur pendant le processus de mise à jour.

Imaginez que j'ai ce code: int * ptr = malloc (8) , c'est un pointeur pour lequel 8 octets sont alloués. Ensuite, j'ai une boucle while qui est sur le point d'attribuer une valeur au pointeur, puis l'incrémentation du pointeur ptr ++ suit. Chaque fois que ce code est exécuté sur l'adresse actuelle du pointeur d' adresse cur , il vérifie si le pointeur est dans les limites spécifiées dans les première et deuxième parties.

C'est le cas dans le nouveau code généré par le compilateur. Un groupe en ligne soulève souvent la question de ce qu'est un «code d'outil». Il s'agit du code généré par le compilateur. En tant que programmeur, vous ne voyez que ce qui est montré à droite - ces 4 lignes. Mais avant cette opération, le compilateur insère un nouveau code C dans l' adresse cur , attribue une valeur au pointeur et vérifie les limites à chaque fois.



Et si, lors de l'utilisation du nouveau code, la valeur dépasse les limites, la fonction est interrompue. C'est ce qu'on appelle le «code d'outil». Cela signifie que vous prenez le code source à l'aide d'un programme C, puis ajoutez le nouveau code source C, puis compilez le nouveau programme. Donc, l'idée de base derrière les pointeurs Fat est assez simple.

Cette approche présente certains inconvénients. Le plus gros inconvénient est la grande taille du pointeur. Et cela signifie que vous ne pouvez pas simplement prendre le "pointeur épais" et le passer tel quel, en dehors de la bibliothèque de shell. Parce qu'on peut s'attendre à ce que le pointeur ait une taille standard, et le programme lui fournira cette taille, à laquelle il «ne rentrera pas», à cause de quoi tout explosera. Il y a aussi des problèmes si vous souhaitez inclure des pointeurs de ce type dans une structure ou quelque chose comme ça, car ils peuvent redimensionner la structure .

Par conséquent, une chose très populaire dans le code C est de prendre quelque chose de la taille d'une structure , puis de faire quelque chose en fonction de cette taille - réserver de l'espace disque pour les structures de cette taille, etc.

Et une chose plus délicate est que ces pointeurs, en règle générale, ne peuvent pas être mis à jour de manière atomique. Pour les architectures 32 bits, il est typique d'écrire une variable 32 bits atomique. Mais les "pointeurs épais" contiennent 3 tailles entières , donc si vous avez du code qui s'attend à ce que le pointeur ait une valeur atomique, vous pourriez avoir des ennuis. Parce que pour effectuer certaines de ces vérifications, vous devez regarder l'adresse actuelle, puis regarder les tailles, puis vous devrez peut-être les augmenter, etc., etc. Ainsi, cela peut provoquer des erreurs très subtiles si vous utilisez du code qui tente de faire des parallèles entre des pointeurs réguliers et épais. Ainsi, vous pouvez utiliser des pointeurs Fat dans certains cas, comme les clôtures Electroc , mais les effets secondaires de leur utilisation sont si importants qu'en pratique normale, ces approches ne sont pas utilisées.

Et maintenant, nous allons parler de la vérification des limites par rapport à la structure des données fantômes. L'idée principale de la structure est que vous savez quelle est la taille de chaque objet que vous allez placer, c'est-à-dire que vous connaissez la taille que vous devez réserver pour cet objet. Ainsi, par exemple, si vous avez un pointeur que vous appelez avec la fonction malloc , vous devez spécifier la taille de l'objet: char xp = malloc (size) .



Si vous avez quelque chose comme une variable statique comme ce char p [256] , le compilateur peut automatiquement déterminer quelles devraient être les limites de son placement.

Par conséquent, pour chacun de ces pointeurs, vous devez en quelque sorte insérer deux opérations. Il s'agit principalement d'arithmétique, comme q = p + 7 , ou quelque chose de similaire. Cette insertion se fait en déréférençant un lien de type deref * q = 'q' . Vous vous demandez peut-être pourquoi vous ne pouvez pas compter sur le lien lors du collage? Pourquoi devons-nous faire ces calculs? Le fait est que lorsque vous utilisez C et c ++, vous avez un pointeur pointant vers une passe vers la fin valide de l'objet à droite, après quoi vous l'utilisez comme condition d'arrêt. Ainsi, vous accédez à l'objet et dès que vous atteignez ce pointeur de fin, vous arrêtez réellement la boucle ou abandonnez l'opération.

Ainsi, si nous ignorons l'arithmétique, nous provoquons toujours une erreur grave, dans laquelle le pointeur dépasse les limites, ce qui peut en fait perturber le travail de nombreuses applications. Nous ne pouvons donc pas simplement insérer le lien, car comment savez-vous que cela se produit en dehors des limites établies? L'arithmétique nous permet de dire s'il en est ainsi ou non, et ici tout sera licite et correct. Parce que ce calage utilisant l'arithmétique vous permet de suivre où se trouve le pointeur par rapport à sa ligne de base d'origine.

La question suivante est donc la suivante: comment mettre en œuvre la validation des frontières? Parce que nous devons en quelque sorte faire correspondre l'adresse spécifique du pointeur avec un certain type d'informations sur les limites de ce pointeur. Et par conséquent, bon nombre de vos décisions précédentes utilisent des éléments tels que, par exemple, une table de hachage ou un arbre, qui vous permet d'effectuer la recherche correcte. Donc, étant donné l'adresse du pointeur, je fais quelques recherches dans cette structure de données et je trouve ses limites. Compte tenu de ces limites, je décide si je peux laisser l'action se produire ou non. Le problème est qu'il s'agit d'une recherche lente, car ces structures de données se ramifient et lorsque vous examinez un arbre, vous devez examiner un tas de ces branches jusqu'à ce que vous trouviez la bonne valeur. Et même s'il s'agit d'une table de hachage, vous devez suivre les chaînes de code et ainsi de suite. Ainsi, nous devons définir une structure de données très efficace qui suit leurs limites, une structure qui rendrait cette vérification très simple et claire. Alors allons-y maintenant.

Mais avant de faire cela, permettez-moi de vous expliquer brièvement comment fonctionne l'approche d' allocation de mémoire entre amis . Parce que c'est l'une des choses qui sont souvent posées.
L'allocation de mémoire d'amis divise la mémoire en partitions qui sont un multiple de puissance de 2 et essaie d'y allouer des demandes de mémoire. Voyons comment cela fonctionne. Au début, l' allocation de contacts traite la mémoire non allouée comme un gros bloc - il s'agit du rectangle supérieur de 128 bits. Ensuite, lorsque vous demandez un bloc plus petit pour l'allocation dynamique, il essaie de diviser cet espace d'adressage en parties par incréments de 2 jusqu'à ce qu'il trouve un bloc suffisant pour vos besoins.

Supposons qu'une demande du type a = malloc (28) soit arrivée, c'est-à-dire une demande d'allocation de 28 octets. Nous avons un bloc de 128 octets qui est trop inutile pour allouer à cette demande. Par conséquent, notre bloc est divisé en deux blocs de 64 octets - de 0 à 64 octets et de 64 octets à 128 octets. Et cette taille est également importante pour notre demande, alors mon ami divise à nouveau un bloc de 64 octets en 2 parties et reçoit 2 blocs de 32 octets.



Moins est impossible, car 28 octets ne conviennent pas et 32 ​​est la taille minimale la plus appropriée. Alors maintenant, ce bloc de 32 octets sera alloué à notre adresse a. Supposons que nous ayons une autre requête pour b = malloc (50) . Buddy vérifie les blocs sélectionnés, et comme 50 est supérieur à la moitié de 64, mais inférieur à 64, place la valeur b dans le bloc le plus à droite.

Enfin, nous avons une autre demande de 20 octets: c = malloc (20) , cette valeur est placée dans le bloc du milieu.



Buddy a une propriété intéressante: lorsque vous libérez de la mémoire dans un bloc et à côté d'un bloc de la même taille, après avoir libéré les deux blocs, buddy combine deux blocs voisins vides en un seul.



Par exemple, lorsque nous donnons la commande free © , nous libérerons le bloc du milieu, mais l'union ne se produira pas, donc le bloc à côté de lui sera toujours occupé. Mais après avoir libéré le premier bloc à l'aide de la commande free (a) , les deux blocs fusionneront en un seul. Ensuite, si nous libérons la valeur de b, les blocs voisins seront à nouveau fusionnés et nous obtiendrons un bloc entier de 128 octets, comme c'était au tout début. L'avantage de cette approche est que vous pouvez facilement trouver où se trouve le copain par simple arithmétique et déterminer les limites de la mémoire. C'est ainsi que l'allocation de mémoire fonctionne avec l'approche d' allocation de mémoire Buddy .

Toutes mes conférences se posent souvent la question, une telle approche n'est-elle pas un gaspillage? Imaginez qu'au début j'avais une demande de 65 octets, je devais lui allouer tout le bloc de 128 octets. Oui, c'est du gaspillage, en fait vous n'avez pas de mémoire dynamique et vous ne pouvez plus allouer de ressources dans le même bloc. Mais là encore, c'est un compromis, car il est très facile de faire un calcul, de faire une fusion, etc. Donc, si vous voulez une allocation de mémoire plus précise, vous devez utiliser une approche différente.

Alors, que fait le système de vérification du rebond du buggy (BBC) ?



Elle effectue plusieurs tours, dont l'un est la séparation du bloc mémoire en 2 parties, dont l'une contient un objet, et la seconde en est un ajout. Ainsi, nous avons 2 types de limites - les limites de l'objet et les limites de la distribution de la mémoire. L'avantage est qu'il n'est pas nécessaire de stocker l'adresse de base, et une recherche rapide à l'aide d'une table de ligne est possible.

Toutes nos tailles de distribution sont 2 à la puissance de n , où n est un entier. Ce principe 2n est appelé puissance de deux . Par conséquent, nous n'avons pas besoin de beaucoup de bits pour imaginer la taille d'une taille de distribution particulière. Par exemple, si la taille du cluster est 16, il vous suffit de sélectionner 4 bits - c'est le concept d'un logarithme, c'est-à-dire que 4 est un exposant de n , dans lequel vous devez augmenter le nombre 2 pour obtenir 16.

Il s'agit d'une approche assez économique de l'allocation de mémoire, car le nombre minimal d'octets est utilisé, mais il doit être un multiple de 2, c'est-à-dire que vous pouvez avoir 16 ou 32, mais pas 33 octets. De plus, la vérification du rebond du buggy vous permet de stocker des informations sur les valeurs limites dans un tableau linéaire (1 octet par enregistrement) et vous permet d'allouer de la mémoire dans 1 emplacement avec une taille de 16 octets. allouer de la mémoire avec une granularité d'emplacement. Qu'est-ce que cela signifie?



Si nous avons un slot de 16 octets où nous allons mettre la valeur p = malloc (16) , alors la valeur du tableau ressemblera à la table [p / slot.size] = 4 .



Supposons que nous devons maintenant placer une valeur de 32 octets de taille p = malloc (32) . Nous devons mettre à jour la table des bordures pour correspondre à la nouvelle taille. Et cela se fait deux fois: d'abord comme table [p / slot.size] = 5 , puis comme table [(p / slot.size) + 1] = 5 - la première fois pour le premier slot, qui est alloué à cette mémoire, et le second fois - pour le deuxième emplacement. Ainsi, nous allouons 32 octets de mémoire. Voici à quoi ressemble le journal de distribution des tailles. Ainsi, pour deux emplacements d'allocation de mémoire, la table des limites est mise à jour deux fois. Est-ce clair? Cet exemple est destiné aux personnes qui doutent que les journaux et les tables aient un sens ou non. Parce que les tables sont multipliées chaque fois que l'allocation de mémoire se produit.

Voyons ce qui se passe avec la table des bordures. Supposons que nous ayons un code C qui ressemble à ceci: p '= p + i , c'est-à-dire que le pointeur p' est obtenu à partir de p en ajoutant une variable i . Alors, comment obtenir la taille de la mémoire allouée à p ? Pour ce faire, vous consultez le tableau à l'aide des conditions logiques suivantes:

size = 1 << table [p >> log de slot_size]



Sur la droite, nous avons la taille des données allouées pour p , qui devrait être 1. Ensuite, vous la déplacez vers la gauche et regardez la table, prenez cette taille de pointeur, puis déplacez-vous vers la droite, où se trouve le journal de la table de taille d'emplacement. Si l'arithmétique fonctionne, alors nous avons correctement lié le pointeur à la table des bordures. Autrement dit, la taille du pointeur doit être supérieure à 1, mais inférieure à la taille de l'emplacement. À gauche, nous avons la valeur, et à droite - la taille de la fente, et la valeur du pointeur est située entre eux.

Supposons que la taille du pointeur soit de 32 octets, puis dans le tableau, à l'intérieur des crochets, nous aurons le nombre 5.

Supposons que nous voulons trouver le mot-clé de base de ce pointeur: base = p & n (taille - 1) . Ce que nous allons faire nous donne une certaine masse, et cette masse nous permettra de restaurer la base située ici. Imaginez que notre taille soit 16, en binaire c'est 16 = ... 0010000. Les points de suspension signifient qu'il y a encore beaucoup de zéros, mais nous nous intéressons à cette unité et aux zéros derrière elle. Si nous considérons (16-1), cela ressemble à ceci: (16-1) = ... 0001111. En code binaire, l'inverse de ceci ressemblera à ceci: ~ (16-1) ... 1110000.





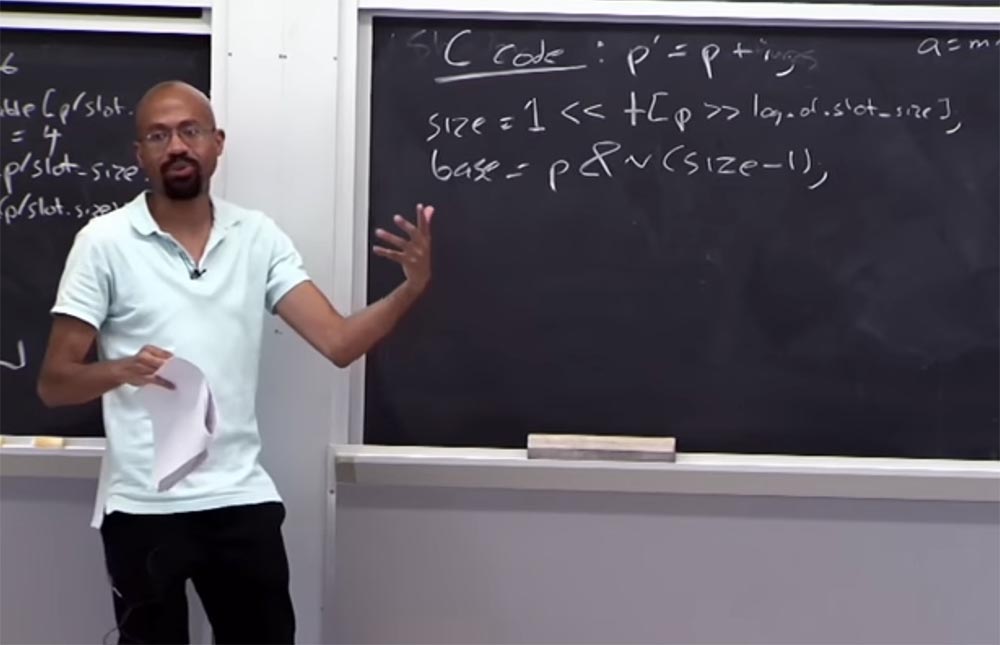
Ainsi, cette chose nous permet essentiellement d'effacer le bit, qui sera essentiellement rendu à partir du pointeur actuel et nous donnera sa base . Grâce à cela, il nous sera très simple de vérifier si ce pointeur se trouve dans les limites. Nous pouvons donc simplement vérifier que (p ')> = base et si la valeur ( p' - base) est inférieure à la taille sélectionnée.



C'est une chose assez simple pour savoir si le pointeur se trouve dans les limites de la mémoire. Je ne vais pas entrer dans les détails, il suffit de dire que toute l'arithmétique binaire est résolue de la même manière. De telles astuces vous permettent d'éviter des calculs plus complexes.

Il existe encore une cinquième propriété de la vérification de rebond de Buggy - elle utilise un système de mémoire virtuelle pour éviter de dépasser les limites définies pour le pointeur. L'idée principale est que si nous avons une telle arithmétique pour le pointeur avec lequel nous déterminons la sortie, alors nous pouvons définir un bit d'ordre élevé pour le pointeur.



Ce faisant, nous garantissons que le déréférencement du pointeur ne causera pas de problèmes matériels. Le fait de régler le bit de poids fort à lui seul ne pose pas de problème; le déréférencement du pointeur peut provoquer un problème.


La version complète du cours est disponible ici .

Merci de rester avec nous. Aimez-vous nos articles? Vous voulez voir des matériaux plus intéressants? Soutenez-nous en passant une commande ou en le recommandant à vos amis, une réduction de 30% pour les utilisateurs Habr sur un analogue unique de serveurs d'entrée de gamme que nous avons inventés pour vous: Toute la vérité sur VPS (KVM) E5-2650 v4 (6 cœurs) 10 Go DDR4 240 Go SSD 1 Gbps à partir de 20 $ ou comment diviser le serveur? (les options sont disponibles avec RAID1 et RAID10, jusqu'à 24 cœurs et jusqu'à 40 Go de DDR4).

Dell R730xd 2 fois moins cher? Nous avons seulement 2 x Intel Dodeca-Core Xeon E5-2650v4 128 Go DDR4 6x480 Go SSD 1 Gbps 100 TV à partir de 249 $ aux Pays-Bas et aux États-Unis! Pour en savoir plus sur la création d'un bâtiment d'infrastructure. classe utilisant des serveurs Dell R730xd E5-2650 v4 coûtant 9 000 euros pour un sou?