Depuis de nombreuses années, je regarde le snooker comme un sport. Il a tout: la beauté envoûtante d'un jeu intellectuel, l'élégance des coups de kiem et la tension psychologique de la compétition. Mais il y a une chose que je n'aime pas - son système de notation .
Son principal inconvénient est qu'il ne prend en compte que le fait de la réussite du tournoi sans tenir compte de la «complexité» des matchs. Le modèle Elo est privé de cet inconvénient, qui surveille la «force» des joueurs et la met à jour en fonction des résultats des matchs et de la «force» de l'adversaire. Cependant, cela ne correspond pas parfaitement: on pense que tous les matchs se déroulent dans des conditions égales, et dans le snooker, ils sont joués jusqu'à un certain nombre d'images gagnées (fêtes). Pour tenir compte de ce fait, j'ai envisagé un autre modèle, que j'ai appelé EloBeta .
Cet article étudie la qualité des modèles Elo et EloBet en fonction des résultats des matchs de snooker. Il est important de noter que les principaux objectifs sont d'évaluer la «force» des joueurs et de créer une note «juste», plutôt que de construire des modèles prédictifs pour gagner du profit.

Le classement actuel du snooker est basé sur les réalisations du joueur dans les tournois avec leur "poids" différent. Il était une fois, seuls les championnats du monde étaient pris en compte. Après l'apparition de nombreuses autres compétitions, une table de points a été développée que le joueur pouvait gagner lorsqu'il atteignait une certaine étape du tournoi. Désormais, le classement prend la forme d'un montant "mobile" de prix que le joueur a gagné au cours des deux (environ) dernières années civiles.
Ce système présente deux avantages principaux: il est simple (gagner beaucoup d'argent - remonter dans le classement) et prévisible (si vous voulez monter jusqu'à un certain endroit - gagner une certaine somme d'argent, toutes choses étant égales par ailleurs). Le problème est qu'avec cette méthode la force (compétence, forme) des adversaires n'est pas prise en compte . Le contre-argument habituel est: «Si un joueur a atteint le stade avancé du tournoi, il est par définition le joueur fort actuel» («les joueurs faibles ne gagnent pas de tournois»). Cela semble assez convaincant. Cependant, dans le snooker, comme dans tout sport, le rôle de l'affaire doit être pris en compte: si un joueur est «plus faible», cela ne signifie pas qu'il ne pourra jamais gagner «plus fort» dans un match contre un joueur. Cela arrive juste moins souvent que le scénario inverse. C'est là que le modèle Elo entre en scène.
L'idée du modèle Elo est que chaque joueur est associé à une note numérique. Une hypothèse est introduite selon laquelle le résultat d'un match entre deux joueurs peut être prédit en fonction de la différence de leurs notes: des valeurs plus élevées signifient une probabilité plus élevée de gagner un joueur «fort» (avec une note plus élevée). La cote Elo est basée sur la "force" actuelle , calculée sur la base des résultats des matchs avec d'autres joueurs. Cela évite une faille majeure dans le système de notation officiel actuel. Cette approche vous permet également de mettre à jour le classement des joueurs pendant le tournoi afin de répondre numériquement à ses bonnes performances.
Ayant une expérience pratique de la cote Elo, il me semble qu'il devrait bien se montrer en snooker. Cependant, il y a un obstacle: il est conçu pour les compétitions avec un seul type de match . Bien sûr, il existe des variantes pour prendre en compte les avantages du terrain à domicile dans le football et le premier coup aux échecs (tous deux sous la forme d'ajouter un nombre fixe de points de classement au joueur avec un avantage). En snooker, les matchs se jouent au format "best of N": le joueur qui remporte les premières victoires n= fracN+12 cadres (fêtes). Nous appellerons également ce format "jusqu'à n victoires. "
Intuitivement, gagner un match de 10 victoires (finale d'un tournoi sérieux) devrait être plus difficile pour un joueur «faible» que de gagner un match de 4 victoires (premier tour des tournois Home Nations en cours). Ceci est pris en compte dans mon modèle EloBet .
L'idée d'utiliser la cote Elo dans le snooker n'est pas nouvelle. Par exemple, il existe les œuvres suivantes:
- Snooker Analyst utilise un système de notation «Elo like» (plus comme un modèle Bradley - Terry ). L'idée est de mettre à jour le classement en fonction de la différence entre le nombre "réel" et "attendu" de trames gagnées. Cette approche soulève des questions. Bien sûr, la plus grande différence dans le nombre d'images montre probablement la plus grande différence de force, mais au départ, le joueur n'a pas une telle tâche. En snooker, l'objectif est "juste" de gagner le match, c'est-à-dire Gagnez un certain nombre d'images devant l'adversaire.
- Cette discussion est sur le forum avec l'implémentation du modèle Elo de base.
- Ceci et ces utilisations sont réelles dans le billard amateur.
- Il y a peut-être d'autres travaux que j'ai ratés. Je serais très reconnaissant pour toute information à ce sujet.
Revue
Cet article est destiné aux utilisateurs de la langue R qui sont intéressés à étudier la notation d'Elo, et aux fans de snooker. Toutes les expériences sont écrites avec l'idée d'être reproductibles. Le code est caché sous des spoilers, a des commentaires et utilise des packages tidyverse , il peut donc être intéressant pour les utilisateurs de lire par lui-même R. On suppose que tout le code présenté est exécuté séquentiellement. Un fichier peut être trouvé ici .
L'article est organisé comme suit:
- La section Modèle décrit les approches d' Elo et d' EloBet avec implémentation dans R.
- La section Expérience décrit les détails et la motivation du calcul: quelles données et méthodologie sont utilisées (et pourquoi), et quels résultats sont obtenus.
- La section EloBet Ranking Study contient les résultats de l'application du modèle EloBet à des données réelles de snooker. Il sera plus intéressé par les amateurs de snooker.
Nous aurons besoin de l'initialisation suivante.
Code d'initialisation# suppressPackageStartupMessages(library(dplyr)) library(tidyr) library(purrr) # library(ggplot2) # suppressPackageStartupMessages(library(comperank)) theme_set(theme_bw()) # . . set.seed(20180703)
Les modèles
Les deux modèles sont basés sur les hypothèses suivantes:
- Il existe un ensemble fixe de joueurs qui doivent être classés de «les plus forts» (première place) à «les plus faibles» (dernière place).
- Classement par association de joueurs i avec évaluation numérique ri : Un nombre représentant la "force" du joueur (une valeur plus élevée signifie un joueur plus fort).
- Plus la différence de notes avant le match est grande, moins la victoire du joueur «faible» (avec une note inférieure) est probable.
- Les notes sont mises à jour après chaque match en fonction de son résultat et des notes antérieures.
- Une victoire sur un adversaire «plus fort» devrait s'accompagner d' une augmentation de note plus importante qu'une victoire sur un adversaire «plus faible». Avec la défaite, le contraire est vrai.
Elo
Code modèle Elo #' @details . #' `...` . #' #' @return , 1 ( `rating1`) #' 2 ( `rating2`). #' . elo_win_prob <- function(rating1, rating2, ksi = 400, ...) { norm_rating_diff <- (rating2 - rating1) / ksi 1 / (1 + 10^norm_rating_diff) } #' @return , #' `comperank::add_iterative_ratings()`. elo_fun_gen <- function(K, ksi = 400) { function(rating1, score1, rating2, score2) { comperank::elo(rating1, score1, rating2, score2, K = K, ksi = ksi)[1, ] } }
Elo Model met à jour les classements selon la procédure suivante:
Calcul de la probabilité qu'un certain joueur gagne le match (avant qu'il ne commence). La probabilité qu'un joueur gagne (nous l'appellerons «premier») avec l'identifiant i et évalué ri sur un autre joueur ("second") avec identifiant j et évalué rj est égal
Pr(ri,rj)= frac11+10(rj−ri)/400
Avec cette approche, le calcul de la probabilité obéit à la troisième hypothèse.
Normaliser la différence à 400 est une manière mathématique de dire quelle différence est considérée comme "grande". Ce nombre peut être remplacé par un paramètre de modèle. xi Cependant, cela n'affecte que la propagation des notations futures et est généralement redondant. Une valeur de 400 est assez standard.
Avec une approche générale, la probabilité de victoire est égale à L(rj−ri) où L(x) une fonction strictement croissante avec des valeurs de 0 à 1. Nous utiliserons la courbe logistique. Une étude plus complète se trouve dans cet article .
Calcul du résultat du match S . Dans le modèle de base, il est égal à 1 en cas de victoire du premier joueur (défaite du second), 0,5 en cas d'égalité et 0 en cas de défaite du premier joueur (victoire du second).
Mise à jour de la note :
- delta=K cdot(S−Pr(ri,rj)) . Il s'agit du montant dont les notes changeront. Elle utilise un coefficient K (le seul paramètre du modèle). Moins K (avec des probabilités égales) signifie un changement plus faible des notes - le modèle est plus conservateur, c.-à-d. plus de victoires sont nécessaires pour "prouver" un changement de force. D'un autre côté, plus K signifie plus de crédibilité avec les résultats récents que les notes actuelles. Le choix de "optimal" K est un moyen de créer un "bon" système de notation .
- r(nouveau)i=ri+ delta , r(nouveau)j=rj− delta .
Remarques :
- Comme le montrent les formules de mise à jour, la somme des notes de tous les joueurs considérés ne change pas au fil du temps: la note augmente en raison d'une diminution de la note de l'adversaire
- Les joueurs sans match joué sont associés à une note initiale de 0. Généralement, des valeurs de 1500 ou 1000 sont utilisées, mais je ne vois pas d'autre raison que psychologique. Compte tenu de la remarque précédente, l'utilisation de zéro signifie que la somme de toutes les notes est toujours nulle, ce qui est beau à sa manière.
- Il est nécessaire de jouer un certain nombre de matchs pour que le classement reflète la "force" du joueur. Cela pose un problème: les nouveaux joueurs commencent avec une note de 0, ce qui n'est probablement pas le plus petit parmi les joueurs actuels. En d'autres termes, les «nouveaux arrivants» sont considérés comme «plus forts» que certains autres joueurs. Vous pouvez essayer de lutter contre cela avec des procédures de mise à jour de notation externe lorsque vous entrez un nouveau joueur.
Pourquoi un tel algorithme a-t-il un sens? En cas d'égalité de notes delta est toujours égal  . Supposons, par exemple, que ri=0 et rj=400 . Cela signifie que la probabilité de gagner le premier joueur est frac11+10 environ0,0909 , c'est-à-dire il / elle gagnera 1 match sur 11.
. Supposons, par exemple, que ri=0 et rj=400 . Cela signifie que la probabilité de gagner le premier joueur est frac11+10 environ0,0909 , c'est-à-dire il / elle gagnera 1 match sur 11.
- En cas de victoire, il recevra une augmentation d'environ
 , ce qui est plus que dans le cas de l'égalité des notations.
, ce qui est plus que dans le cas de l'égalité des notations. - En cas de défaite, il recevra une réduction d'environ
 , ce qui est moins qu'en cas d'égalité des notations.
, ce qui est moins qu'en cas d'égalité des notations.
Cela montre que le modèle Elo obéit à la cinquième hypothèse: une victoire sur un adversaire est «plus forte» s'accompagne d' une augmentation de note plus importante qu'une victoire sur un adversaire est «plus faible», et vice versa.
Bien sûr, le modèle Elo a ses propres caractéristiques pratiques (plutôt de haut niveau). Cependant, le plus important pour notre étude est le suivant: on suppose que tous les matches se déroulent sur un pied d'égalité. Cela signifie que la distance du match n'est pas prise en compte: une victoire dans un match jusqu'à 4 victoires est récompensée de la même manière qu'une victoire dans un match jusqu'à 10 victoires. Voici le modèle de scène EloBeta.
EloBeta
Code modèle EloBet #' @details . #' #' @return , 1 ( `rating1`) #' 2 ( `rating2`). `frames_to_win` #' . #' . elobeta_win_prob <- function(rating1, rating2, frames_to_win, ksi = 400, ...) { prob_frame <- elo_win_prob(rating1 = rating1, rating2 = rating2, ksi = ksi) # , `frames_to_win` # # (`prob_frame`). . pbeta(prob_frame, frames_to_win, frames_to_win) } #' @return : 1 / #' (), 0.5 0 / (). get_match_result <- function(score1, score2) { # () , . near_score <- dplyr::near(score1, score2) dplyr::if_else(near_score, 0.5, as.numeric(score1 > score2)) } #' @return , #' `add_iterative_ratings()`. elobeta_fun_gen <- function(K, ksi = 400) { function(rating1, score1, rating2, score2) { prob_win <- elobeta_win_prob( rating1 = rating1, rating2 = rating2, frames_to_win = pmax(score1, score2), ksi = ksi ) match_result <- get_match_result(score1, score2) delta <- K * (match_result - prob_win) c(rating1 + delta, rating2 - delta) } }
Dans le modèle Elo, la différence de notes affecte directement la probabilité de gagner la totalité du match. L'idée principale du modèle EloBet est l' influence directe de la différence de notes sur la probabilité de gagner dans une trame et le calcul explicite de la probabilité qu'un joueur gagne n images devant l'adversaire .
La question demeure: comment calculer une telle probabilité? Il s'avère que c'est l'un des problèmes les plus anciens de l'histoire de la théorie des probabilités et qu'il a son propre nom - le problème de la division des paris (problème des points). Une très belle présentation se trouve dans cet article . En utilisant sa notation, la probabilité souhaitée est:
P(n,n)= sum limits2n−1j=n2n−1 choisissezjpj(1−p)2n−1−j
Ici P(n,n) - probabilité que le premier joueur remporte le match avant n victoires; p - la probabilité de sa victoire dans une même image (l'adversaire a une probabilité 1−p ) Avec cette approche, on suppose que les résultats de trame dans la correspondance sont indépendants les uns des autres . Cela peut être mis en doute, mais c'est une hypothèse nécessaire pour ce modèle.
Existe-t-il un moyen plus rapide de calculer? Il s'avère que la réponse est oui. Après plusieurs heures de conversion de formule, d'expériences pratiques et de recherches sur Internet, j'ai trouvé la propriété suivante sur une fonction bêta incomplète régularisée Ix(a,b) . Substitution m=k, n=2k−1 dans cette propriété et en remplaçant k sur n il s'avère P(n,n)=Ip(n,n) .
C'est également une bonne nouvelle pour les utilisateurs de R, car Ip(n,n) peut être calculé comme pbeta(p, n, n) . Remarque : le cas général de la probabilité de victoire dans n images avant que l'adversaire gagne m peut également être calculé comme Ip(n,m) et pbeta(p, n, m) respectivement. Cela ouvre de grandes opportunités pour mettre à jour la probabilité de gagner pendant le match .
La procédure de mise à jour des notations dans le cadre du modèle EloBet se présente sous la forme suivante (avec notations connues ri et rj nombre d'images nécessaires pour gagner n et le résultat du match S , comme dans le modèle Elo):
- Calcul de la probabilité de victoire du premier joueur dans une même trame : p=Pr(ri,rj)= frac11+10(rj−ri)/400 .
- Calcul de la probabilité de victoire de ce joueur dans le match : PrBeta(ri,rj)=Ip(n,n) . Par exemple, si p égal à 0,4, puis la probabilité de gagner le match avant 4 victoires tombe à 0,29, et dans "à 18 victoires" - à 0,11.
- Mise à jour de la note :
- delta=K cdot(S−PrBeta(ri,rj)) .
- r(nouveau)i=ri+ delta , r(nouveau)j=rj− delta .
Remarque : car la différence de notes affecte directement la probabilité de gagner dans une trame, et non dans l'ensemble du match, une valeur de coefficient optimal inférieure devrait être attendue K : partie de la valeur delta vient d'un effet renforçant PrBeta(ri,rj) .
L'idée de calculer le résultat d'un match sur la base de la probabilité de gagner dans une trame n'est pas très nouvelle. Sur ce site d' auteur François Labelle , vous pouvez trouver un calcul en ligne de la probabilité de gagner le «meilleur de N "Le match, ainsi que d'autres fonctions. J'étais heureux de voir que nos résultats de calcul coïncident. Cependant, je n'ai trouvé aucune source pour introduire une telle approche à la procédure de mise à jour des notes Elo. Comme auparavant, je serai très reconnaissant pour toute information sur ce sujet.
Je n'ai pu trouver cet article et cette description du système Elo que sur le serveur de jeu de backgammon (FIBS). Il existe également un analogue en russe . Ici, différentes durées de correspondance sont prises en compte en multipliant la différence de notes par la racine carrée de la distance de correspondance. Cependant, il ne semble pas avoir de justification théorique.
Une expérience
Une expérience a plusieurs objectifs. Sur la base des résultats des matchs de snooker:
- Déterminer les meilleures valeurs de coefficient K pour les deux modèles.
- Etudier la stabilité des modèles en termes de précision de probabilité prédictive.
- Pour étudier l'effet de l'utilisation de tournois «sur invitation» sur les cotes.
- Créez un historique de notation équitable pour la saison 2017/18 pour tous les joueurs professionnels.
Les données
Code de génération de données d'expérience # "train", "validation" "test" split_cases <- function(n, props = c(0.5, 0.25, 0.25)) { breaks <- n * cumsum(head(props, -1)) / sum(props) id_vec <- findInterval(seq_len(n), breaks, left.open = TRUE) + 1 c("train", "validation", "test")[id_vec] } pro_players <- snooker_players %>% filter(status == "pro") # pro_matches_all <- snooker_matches %>% # filter(!walkover1, !walkover2) %>% # semi_join(y = pro_players, by = c(player1Id = "id")) %>% semi_join(y = pro_players, by = c(player2Id = "id")) %>% # 'season' left_join( y = snooker_events %>% select(id, season), by = c(eventId = "id") ) %>% # arrange(endDate) %>% # widecr transmute( game = seq_len(n()), player1 = player1Id, score1, player2 = player2Id, score2, matchId = id, endDate, eventId, season, # ("train", "validation" "test") # 50/25/25 matchType = split_cases(n()) ) %>% # widecr as_widecr() # (, # , Championship League). pro_matches_off <- pro_matches_all %>% anti_join( y = snooker_events %>% filter(type == "Invitational"), by = c(eventId = "id") ) # get_split <- . %>% count(matchType) %>% mutate(share = n / sum(n)) # 50/25/25 (train/validation/test) pro_matches_all %>% get_split() ## # A tibble: 3 x 3 ## matchType n share ## <chr> <int> <dbl> ## 1 test 1030 0.250 ## 2 train 2059 0.5 ## 3 validation 1029 0.250 # , # . , # __ __, `pro_matches_all`. # , __ # __. pro_matches_off %>% get_split() ## # A tibble: 3 x 3 ## matchType n share ## <chr> <int> <dbl> ## 1 test 820 0.225 ## 2 train 1810 0.497 ## 3 validation 1014 0.278 # K k_grid <- 1:100
Nous utiliserons les données de snooker du package comperank . La source originale est snooker.org . Les résultats sont tirés des correspondances suivantes:
- Le match a été joué au cours de la saison 2016/17 ou 2017/18 .
- Le match fait partie d'un tournoi de snooker «professionnel» , c'est-à-dire:
- Il est du type «Invitational», «Qualifying» ou «Ranking». Nous distinguerons également deux séries de matches: «tous les matchs» (de toutes les données du tournoi) et «matchs officiels» (à l'exclusion des tournois sur invitation). Il y a deux raisons à cela:
- Dans les tournois sur invitation, tous les joueurs n'ont pas la possibilité de changer leur classement. Ce n'est pas nécessairement mauvais dans le cadre des modèles Elo et EloBet, mais cela a une «teinte d'injustice».
- On croit que les joueurs «ne prennent au sérieux» que les matchs de classement officiel. Remarque : la plupart des tournois sur invitation font partie de la Championship League, qui, je pense, est acceptée par la plupart des joueurs.
pas très au sérieux sous forme de pratique avec la capacité de gagner de l'argent. La présence de ces tournois peut affecter le classement. En plus de la "Championship League", il existe d'autres tournois sur invitation: "2016 China Championship", les deux "Champion of Champions", les deux "Masters", "2017 Hong Kong Masters", "2017 World Games", "2017 Romanian Masters".
- Décrit un snooker traditionnel (pas 6 rouges ou Power Snooker) entre des joueurs individuels (pas des équipes).
- Les deux sexes peuvent être impliqués (pas seulement les hommes ou les femmes).
- Les joueurs de tous âges peuvent y participer (pas seulement les seniors ou les "moins de 21 ans).
- Ce n'est pas un "Shoot-Out" car ces tournois sont par ailleurs stockés dans la base de données snooker.org.
- Le match a vraiment eu lieu : son résultat est le résultat d'un vrai match impliquant les deux joueurs.
- Le match se déroule entre deux professionnels . La liste des professionnels est prise pour la saison 2017/18 (131 joueurs). Cette décision semble être la plus controversée, car la suppression des matchs impliquant des "blinds" amateurs à la défaite des professionnels de l'amateur. Cela conduit à un avantage indu de ces joueurs. Il me semble qu'une telle décision est nécessaire pour réduire l' inflation de notation qui se produira lors de la prise en compte des matchs avec des amateurs. Une autre approche consiste à étudier ensemble professionnels et amateurs, mais cela semble déraisonnable dans le cadre de cette étude. La défaite d'un amateur professionnel est considérée comme une perte de la possibilité d'augmenter la cote.
Le nombre final de matches utilisés est de 4118 pour «tous les matchs» et de 3644 pour les «matchs officiels» (respectivement 62,9 et 55,6 par joueur).
Méthodologie
Code de fonction d'expérience #' @param matches `longcr` `widecr` `matchType` #' ( : "train", "validation" "test"). #' @param test_type . #' #' ("") . , #' `game`. #' @param k_vec K . #' @param rate_fun_gen , K #' `add_iterative_ratings()`. #' @param get_win_prob #' (`rating1`, `rating2`) , #' (`frames_to_win`). ____: #' . #' @param initial_ratings #' `add_iterative_ratings()`. #' #' @details : #' - `matches` #' `game`. #' - `test_type`: #' - 1. #' - : 1 / #' (), 0.5 0 / (). #' - RMSE: , #' "" - . #' #' @return Tibble 'k' K 'goodness' #' RMSE. compute_goodness <- function(matches, test_type, k_vec, rate_fun_gen, get_win_prob, initial_ratings = 0) { cat("\n") map_dfr(k_vec, function(cur_k) { # cat(cur_k, " ") matches %>% arrange(game) %>% add_iterative_ratings( rate_fun = rate_fun_gen(cur_k), initial_ratings = initial_ratings ) %>% left_join(y = matches %>% select(game, matchType), by = "game") %>% filter(matchType %in% test_type) %>% mutate( # framesToWin = pmax(score1, score2), # 1 `framesToWin` winProb = get_win_prob( rating1 = rating1Before, rating2 = rating2Before, frames_to_win = framesToWin ), result = get_match_result(score1, score2), squareError = (result - winProb)^2 ) %>% summarise(goodness = sqrt(mean(squareError))) }) %>% mutate(k = k_vec) %>% select(k, goodness) } #' `compute_goodness()` compute_goodness_wrap <- function(matches_name, test_type, k_vec, rate_fun_gen_name, win_prob_fun_name, initial_ratings = 0) { matches_tbl <- get(matches_name) rate_fun_gen <- get(rate_fun_gen_name) get_win_prob <- get(win_prob_fun_name) compute_goodness( matches_tbl, test_type, k_vec, rate_fun_gen, get_win_prob, initial_ratings ) } #' #' #' @param test_type `test_type` ( ) #' `compute_goodness()`. #' @param rating_type ( ). #' @param data_type . #' @param k_vec,initial_ratings `compute_goodness()`. #' #' @details #' . #' , , #' : #' - "pro_matches_" + `< >` + `< >` . #' - `< >` + "_fun_gen" . #' - `< >` + "_win_prob" , #' . #' #' @return Tibble : #' - __testType__ <chr> : . #' - __ratingType__ <chr> : . #' - __dataType__ <chr> : . #' - __k__ <dbl/int> : K. #' - __goodness__ <dbl> : . do_experiment <- function(test_type = c("validation", "test"), rating_type = c("elo", "elobeta"), data_type = c("all", "off"), k_vec = k_grid, initial_ratings = 0) { crossing( testType = test_type, ratingType = rating_type, dataType = data_type ) %>% mutate( dataName = paste0("pro_matches_", testType, "_", dataType), kVec = rep(list(k_vec), n()), rateFunGenName = paste0(ratingType, "_fun_gen"), winProbFunName = paste0(ratingType, "_win_prob"), initialRatings = rep(list(initial_ratings), n()), experimentData = pmap( list(dataName, testType, kVec, rateFunGenName, winProbFunName, initialRatings), compute_goodness_wrap ) ) %>% unnest(experimentData) %>% select(testType, ratingType, dataType, k, goodness) }
"" K K=1,2,...,100 . , . :
- K :
- . , .
add_iterative_ratings() comperank . " ", .. . - , ( ) , . RMSE ( ) ( ). , RMSE=√1|T|∑t∈T(St−Pt)2 où T — , |T| — , St — , Pt — ( ). , " " .
- Valeur K RMSE . "" , RMSE K ( ). 0.5 ( "" 0.5) .
, : "train" (), "validation" () "test" (). , .. "train"/"validation" , "validation"/"test". 50/25/25 " ". " " " " . : 49.7/27.8/22.5. , , .
:
- : .
- : " " " " ( ". ").
- : "" ( "validation" RMSE "" "train" ) "" ( "test" RMSE "" "train" "validation" ).
Résultats
pro_matches_validation_all <- pro_matches_all %>% filter(matchType != "test") pro_matches_validation_off <- pro_matches_off %>% filter(matchType != "test") pro_matches_test_all <- pro_matches_all pro_matches_test_off <- pro_matches_off
# experiment_tbl <- do_experiment()
plot_data <- experiment_tbl %>% unite(group, ratingType, dataType) %>% mutate( testType = recode( testType, validation = "", test = "" ), groupName = recode( group, elo_all = ", ", elo_off = ", . ", elobeta_all = ", ", elobeta_off = ", . " ), # groupName = factor(groupName, levels = unique(groupName)) ) compute_optimal_k <- . %>% group_by(testType, groupName) %>% slice(which.min(goodness)) %>% ungroup() compute_k_labels <- . %>% compute_optimal_k() %>% mutate(label = paste0("K = ", k)) %>% group_by(groupName) %>% # K , # . - # . mutate(hjust = - (k == max(k)) * 1.1 + 1.05) %>% ungroup() plot_experiment_results <- function(results_tbl) { ggplot(results_tbl) + geom_hline( yintercept = 0.5, colour = "#AA5555", size = 0.5, linetype = "dotted" ) + geom_line(aes(k, goodness, colour = testType)) + geom_vline( data = compute_optimal_k, mapping = aes(xintercept = k, colour = testType), linetype = "dashed", show.legend = FALSE ) + geom_text( data = compute_k_labels, mapping = aes(k, Inf, label = label, hjust = hjust), vjust = 1.2 ) + facet_wrap(~ groupName) + scale_colour_manual( values = c(`` = "#377EB8", `` = "#FF7F00"), guide = guide_legend(title = "", override.aes = list(size = 4)) ) + labs( x = " K", y = " (RMSE)", title = " ", subtitle = paste0( ' ( ) ', ' .\n', ' K ( ', '"") , .' ) ) + theme(title = element_text(size = 13), strip.text = element_text(size = 12)) } plot_experiment_results(plot_data)
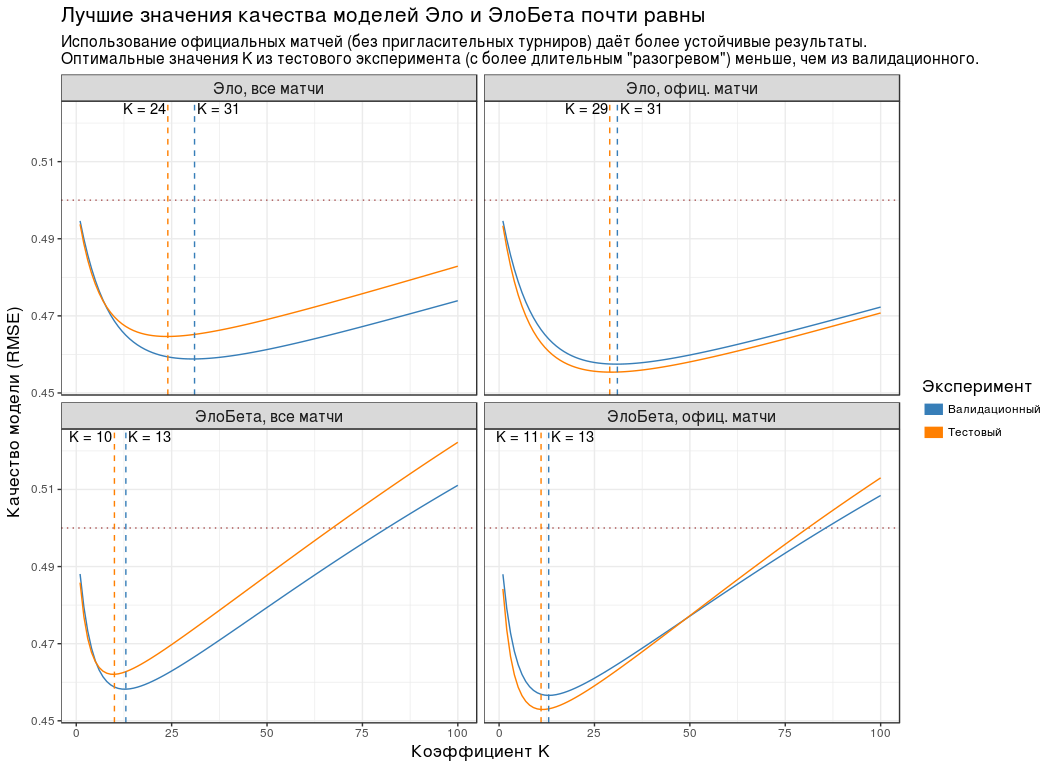
:
- , K , .
- ( "" "" ). , . - "Championship League": 3 .
- RMSE K . , RMSE K "" "". , " " .
- K ( "") , . "", .
- RMSE . 0.5. .
| K | RMSE |
|---|
| , | 24 | 0.465 |
| , . | 29 | 0.455 |
| , | 10 | 0.462 |
| , . | 11 | 0.453 |
Parce que , K " " ( ) 5: 30, — 10.
, K=30 K=10 . , n , .
" " ( K=10 ) - .
-16 2017/18
-16 2017/18 # gather_to_longcr <- function(tbl) { bind_rows( tbl %>% select(-matches("2")) %>% rename_all(funs(gsub("1", "", .))), tbl %>% select(-matches("1")) %>% rename_all(funs(gsub("2", "", .))) ) %>% arrange(game) } # K best_k <- experiment_tbl %>% filter(testType == "test", ratingType == "elobeta", dataType == "off") %>% slice(which.min(goodness)) %>% pull(k) #!!! "" , .. !!! best_k <- round(best_k / 5) * 5 # elobeta_ratings <- rate_iterative( pro_matches_test_off, elobeta_fun_gen(best_k), initial_ratings = 0 ) %>% rename(ratingEloBeta = rating_iterative) %>% arrange(desc(ratingEloBeta)) %>% left_join( y = snooker_players %>% select(id, playerName = name), by = c(player = "id") ) %>% mutate(rankEloBeta = order(ratingEloBeta, decreasing = TRUE)) %>% select(player, playerName, ratingEloBeta, rankEloBeta) elobeta_top16 <- elobeta_ratings %>% filter(rankEloBeta <= 16) %>% mutate( rankChr = formatC(rankEloBeta, width = 2, format = "d", flag = "0"), ratingEloBeta = round(ratingEloBeta, 1) ) official_ratings <- tibble( player = c( 5, 1, 237, 17, 12, 16, 224, 30, 68, 154, 97, 39, 85, 2, 202, 1260 ), rankOff = c( 2, 3, 4, 1, 5, 7, 6, 13, 16, 10, 8, 9, 26, 17, 12, 23 ), ratingOff = c( 905750, 878750, 751525, 1315275, 660250, 543225, 590525, 324587, 303862, 356125, 453875, 416250, 180862, 291025, 332450, 215125 ) )
-16 2017/18 ( snooker.org):
| | | . | . note | |
|---|
| Ronnie O'Sullivan | 1 | 128.8 | 2 | 905 750 | 1 |
| Mark J Williams | 2 | 123,4 | 3 | 878 750 | 1 |
| John Higgins | 3 | 112.5 | 4 | 751 525 | 1 |
| Mark Selby | 4 | 102.4 | 1 | 1 315 275 | -3 |
| Judd Trump | 5 | 92,2 | 5 | 660 250 | 0 |
| Barry Hawkins | 6 | 83.1 | 7 | 543 225 | 1 |
| Ding Junhui | 7 | 82,8 | 6 | 590 525 | -1 |
| Stuart Bingham | 8 | 74,3 | 13 | 324 587 | 5 |
| Ryan Day | 9 | 71.9 | 16 | 303 862 | 7 |
| Neil Robertson | 10 | 70.6 | 10 | 356 125 | 0 |
| Shaun Murphy | 11 | 70.1 | 8 | 453 875 | -3 |
| Kyren Wilson | 12 | 70.1 | 9 | 416 250 | -3 |
| Jack Lisowski | 13 | 68,8 | 26 | 180 862 | 13 |
| Stephen Maguire | 14 | 63,7 | 17 | 291 025 | 3 |
| Mark Allen | 15 | 63,7 | 12 | 332 450 | -3 |
| Yan Bingtao | 16 | 61,6 | 23 | 215 125 | 7 |
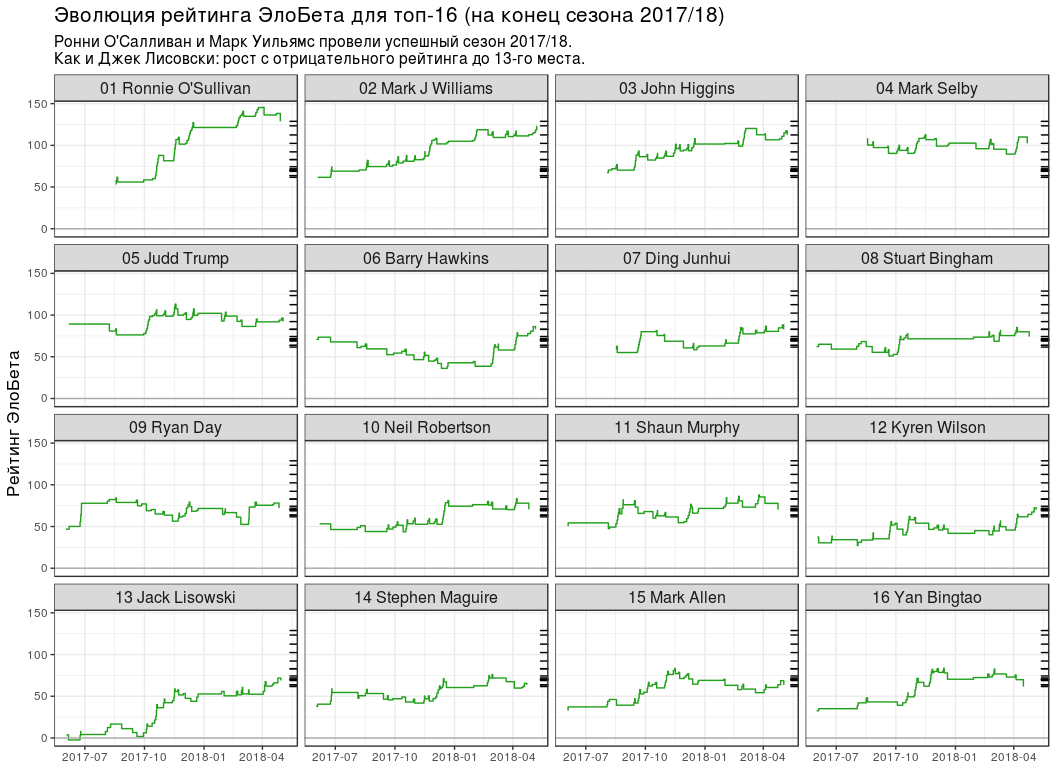
:
- №1 3 . , , ( ).
- "" ( 13 ), ( 7 ).
- 5 . , 6 - WPBSA. , - "" . : , — .
- .
- ( №11), (№14) (№15) -16. "" (№26), (№23) (№17).
. , №16 (Yan Bingtao) №1 (Ronnie O'Sullivan) 0.404. 4 0.299, " 10 " — 0.197 18 — 0.125. , .
# seasons_break <- ISOdatetime(2017, 5, 2, 0, 0, 0, tz = "UTC") # elobeta_history <- pro_matches_test_off %>% add_iterative_ratings(elobeta_fun_gen(best_k), initial_ratings = 0) %>% gather_to_longcr() %>% left_join(y = pro_matches_test_off %>% select(game, endDate), by = "game") # plot_all_elobeta_history <- function(history_tbl) { history_tbl %>% mutate(isTop16 = player %in% elobeta_top16$player) %>% ggplot(aes(endDate, ratingAfter, group = player)) + geom_step(data = . %>% filter(!isTop16), colour = "#C2DF9A") + geom_step(data = . %>% filter(isTop16), colour = "#22A01C") + geom_hline(yintercept = 0, colour = "#AAAAAA") + geom_vline( xintercept = seasons_break, linetype = "dotted", colour = "#E41A1C", size = 1 ) + geom_text( x = seasons_break, y = Inf, label = " 2016/17", colour = "#E41A1C", hjust = 1.05, vjust = 1.2 ) + scale_x_datetime(date_labels = "%Y-%m") + labs( x = NULL, y = " ", title = paste0( " -16 2016/17" ), subtitle = paste0( " ", " ." ) ) + theme(title = element_text(size = 13)) } plot_all_elobeta_history(elobeta_history)
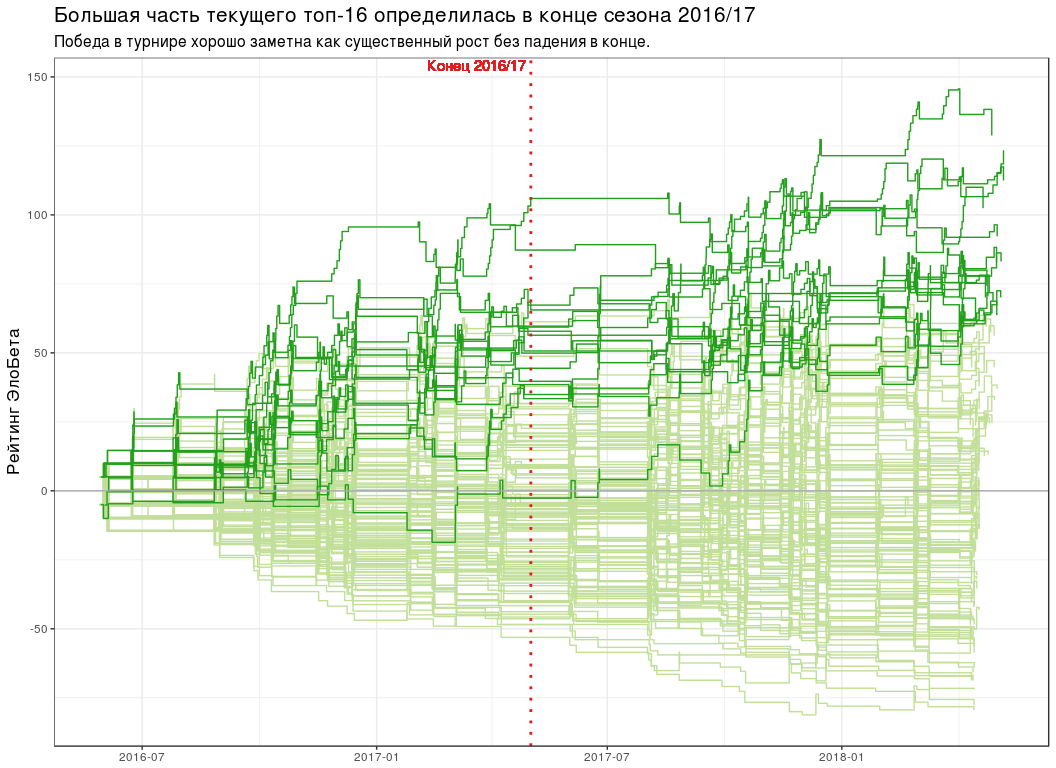
-16
-16 # top16_rating_evolution <- elobeta_history %>% # `inner_join` `elobeta_top16` inner_join(y = elobeta_top16 %>% select(-ratingEloBeta), by = "player") %>% # 2017/18 semi_join( y = pro_matches_test_off %>% filter(season == 2017), by = "game" ) %>% mutate(playerLabel = paste(rankChr, playerName)) # plot_top16_elobeta_history <- function(elobeta_history) { ggplot(elobeta_history) + geom_step(aes(endDate, ratingAfter, group = player), colour = "#22A01C") + geom_hline(yintercept = 0, colour = "#AAAAAA") + geom_rug( data = elobeta_top16, mapping = aes(y = ratingEloBeta), sides = "r" ) + facet_wrap(~ playerLabel, nrow = 4, ncol = 4) + scale_x_datetime(date_labels = "%Y-%m") + labs( x = NULL, y = " ", title = " -16 ( 2017/18)", subtitle = paste0( " ' 2017/18.\n", " : 13- ." ) ) + theme(title = element_text(size = 13), strip.text = element_text(size = 12)) } plot_top16_elobeta_history(top16_rating_evolution)
Conclusions
- " " R :
pbeta(p, n, m) . - — "best of N " ( n ). .
- K=30 K=10 .
- :
sessionInfo() ## R version 3.4.4 (2018-03-15) ## Platform: x86_64-pc-linux-gnu (64-bit) ## Running under: Ubuntu 16.04.4 LTS ## ## Matrix products: default ## BLAS: /usr/lib/openblas-base/libblas.so.3 ## LAPACK: /usr/lib/libopenblasp-r0.2.18.so ## ## locale: ## [1] LC_CTYPE=ru_UA.UTF-8 LC_NUMERIC=C ## [3] LC_TIME=ru_UA.UTF-8 LC_COLLATE=ru_UA.UTF-8 ## [5] LC_MONETARY=ru_UA.UTF-8 LC_MESSAGES=ru_UA.UTF-8 ## [7] LC_PAPER=ru_UA.UTF-8 LC_NAME=C ## [9] LC_ADDRESS=C LC_TELEPHONE=C ## [11] LC_MEASUREMENT=ru_UA.UTF-8 LC_IDENTIFICATION=C ## ## attached base packages: ## [1] stats graphics grDevices utils datasets methods base ## ## other attached packages: ## [1] bindrcpp_0.2.2 comperank_0.1.0 comperes_0.2.0 ggplot2_2.2.1 ## [5] purrr_0.2.5 tidyr_0.8.1 dplyr_0.7.6 ## ## loaded via a namespace (and not attached): ## [1] Rcpp_0.12.17 knitr_1.20 bindr_0.1.1 magrittr_1.5 ## [5] munsell_0.5.0 tidyselect_0.2.4 colorspace_1.3-2 R6_2.2.2 ## [9] rlang_0.2.1 highr_0.7 plyr_1.8.4 stringr_1.3.1 ## [13] tools_3.4.4 grid_3.4.4 gtable_0.2.0 utf8_1.1.4 ## [17] cli_1.0.0 htmltools_0.3.6 lazyeval_0.2.1 yaml_2.1.19 ## [21] assertthat_0.2.0 rprojroot_1.3-2 digest_0.6.15 tibble_1.4.2 ## [25] crayon_1.3.4 glue_1.2.0 evaluate_0.10.1 rmarkdown_1.10 ## [29] labeling_0.3 stringi_1.2.3 compiler_3.4.4 pillar_1.2.3 ## [33] scales_0.5.0 backports_1.1.2 pkgconfig_2.0.1