Théorie du bonheur. Zèbre de loi et file d'attente extraterrestre

Je continue de familiariser les lecteurs de Habr avec les chapitres de son livre "Theory of Happiness" avec le sous-titre "Mathematical Foundations of the Laws of Meanness". Ce livre de science populaire n'est pas encore publié, racontant de manière très informelle comment les mathématiques vous permettent de regarder le monde et la vie des gens avec un nouveau degré de conscience. C'est pour ceux qui s'intéressent à la science et pour ceux qui s'intéressent à la vie. Et puisque notre vie est complexe et, dans l'ensemble, imprévisible, l'accent dans le livre est principalement sur la théorie des probabilités et les statistiques mathématiques. Ici les théorèmes ne sont pas prouvés et les fondements de la science ne sont pas donnés, ce n'est en aucun cas un manuel, mais ce qu'on appelle la science récréative. Mais c'est précisément une telle approche presque ludique qui nous permet de développer l'intuition, d'égayer les cours pour les étudiants avec des exemples vivants et, enfin, d'expliquer aux non-mathématiciens et à nos enfants ce que nous avons trouvé si intéressant dans notre science sèche.





Nous parlerons de Fatum, des tremblements de terre, des files d'attente et des processus merveilleux: l'écoulement de Poisson, la marche aléatoire et un peu des chaînes de Markov.

Loi zèbre

Ils disent que la vie est comme un zèbre: soit une bande blanche soit une noire ... Et il arrive aussi qu'un autre s'ajoute à un problème, et c'est si difficile dans la vie, et puis le chat a commencé à donner naissance! C'est épais, c'est vide! Un à un! Mais le plus triste, c'est que lorsqu'une séquence lumineuse est arrivée et que dans la vie, de mauvaises pensées se glissent: ooh, je ne le ferais pas, ooh, ne serait-il pas nécessaire de payer pour le bonheur ... Une sensation familière? A cette occasion, une des lois de la merphologie est formulée - la deuxième loi de Chisholm: " Quand les choses vont bien, quelque chose devrait arriver dans un avenir très proche ." Mais comme Francis Chisholm, dans son travail original, ne fournit pas une analyse détaillée ou des preuves de cette loi, nous allons essayer de découvrir par nous-mêmes si une régularité se cache derrière cela, ou cela nous semble juste. Et si ce sont les caprices des mathématiques, est-il possible de déterminer la durée ou la fréquence caractéristique des rayures sur le corps de notre zèbre, et de quoi dépend-elle?

Dans la vie, les événements se produisent tout le temps. Parfois, ils ne sont pas du tout connectés les uns aux autres, parfois ils forment des chaînes de relations de cause à effet. Les discussions sur ces connexions, ces chaînes et le chemin de vie prédéterminé peuvent nous mener très loin et nous en parlerons plus tard. En attendant, essayons, comme toujours, de nous en sortir avec la plus petite quantité de données d'entrée pour l'analyse de notre loi. Considérez une séquence d'événements sans rapport les uns avec les autres et voyez ce que vous pouvez en tirer.

Les événements qui ne sont aucunement liés et se produisent dans le temps sont décrits de manière aléatoire en utilisant le flux de Poisson bien connu. Cela correspond à de nombreux phénomènes aléatoires, des tremblements de terre à l'apparition des clients dans le magasin. Le flux d'événements de Poisson est caractérisé par l' intensité ou la densité du flux - un paramètre qui détermine le nombre prévu d'événements par unité de temps. Par exemple, lors de la mesure du temps en jours, la valeur du paramètre $$$\ lambda = 1/7$il y aura une chaîne d'événements aléatoires, en moyenne, se produisant une fois par semaine. Cela ne signifie pas que les événements se produiront avec une fréquence d' une fois par semaine. Une séquence d'événements peut ne pas avoir de fréquence allouée du tout. Il est préférable d'imaginer un flux de Poisson avec une intensité d'une fois par semaine comme ceci: 52 semaines dans une année, ce qui signifie qu'environ 52 événements devraient se produire par an (en moyenne, sur plusieurs années). Si nous choisissons 52 dates aléatoires uniformément réparties dans une année, alors elles peuvent être considérées comme les moments de l'émergence d'événements de Poisson complètement indépendants.


Un exemple de construction d'un ruisseau de Poisson avec une intensité de 1/7 (le temps est mesuré en jours). Sur un intervalle de 365 jours, 52 événements non liés les uns aux autres ont été dispersés au hasard.

De plus, il n'est pas question de périodicité dans ces événements, quand ils le souhaitent, alors cela arrivera. Mais même dans ce pétrin, les statistiques peuvent nous montrer certains modèles. Par exemple, la distribution de la durée des périodes entre les événements illustrés dans la figure précédente ne sera pas uniforme du tout.


La densité de la distribution des durées des écarts entre 52 événements dispersés au hasard sur l'intervalle de 365 jours.

La distribution des durées des intervalles tend à être exponentielle , elle est représentée par un trait plein. Pour cette distribution, le maximum (mode) est à zéro, et la valeur moyenne est exactement de 7 jours. De plus, l'écart type sera également égal à 7 jours. L'égalité de l'écart-type et de la valeur moyenne est une propriété caractéristique de la distribution exponentielle. Comme vous pouvez le voir, ces caractéristiques ne garantissent pas du tout qu'une semaine se passera entre les événements, en moyenne - oui, mais plus souvent - moins, d'ailleurs, des intervalles assez longs peuvent être observés. Enfin, la médiane montre que la moitié de tous les intervalles auront une durée ne dépassant pas 5 jours. L'intensité et la fréquence ne sont pas du tout la même chose, c'est un point très important!

Pour être juste, supposons que les bons et les mauvais événements se produisent tout aussi probablement, mais les événements brillants et significatifs se produisent beaucoup moins souvent que les événements petits et insignifiants. Que ce soit une vie normale dans laquelle la coloration émotionnelle des événements obéit à la distribution normale (gaussienne). Voici à quoi pourrait ressembler une année de destin synthétique, comme une série de vicissitudes de vie aléatoires absolument indépendantes:

Une série d'événements de différentes couleurs émotionnelles, formant un flux de Poisson d'une intensité de 2/7 (2 événements en 7 jours).

Bien qu'aucune bande ne soit observée, il y a plutôt du bruit. Chaque événement passe sans laisser de trace, ne laissant rien dans la mémoire ou l'humeur. Cela ne se produit pas, donnons un souvenir à notre héros modèle, pour commencer, idéal. Chaque événement peut être enfoui à jamais dans sa mémoire et dans son humeur, respectivement, en l’améliorant ou en l’aggravant. Voici une image que nous pouvons obtenir en observant le sort de notre héros pendant dix ans.

Les événements, fusionnant dans la mémoire, forment la coloration émotionnelle de la «vie synthétique».

Bon, bon, on voit déjà une sorte d'alternance d'humeur, mais la photo est sortie pas très joyeuse. Notre héros, après une série de sautes d'humeur, est tombé dans une profonde dépression. Dommage. Essayons encore quelques destins. Tous éprouvent une série de rayures claires et sombres, mais pendant longtemps ils sont enlisés dans un désir désespéré ou dans un bonheur transcendant. Cela se produit, bien sûr, mais c'est clairement anormal.

Quelques exemples de «destins synthétiques» de personnes aux souvenirs parfaits.

Détendez-vous, mec!

Nous avons décrit notre destin de modèle comme un processus très remarquable, il est appelé marche aléatoire unidimensionnelle et possède un certain nombre de propriétés inhabituelles, parmi lesquelles il y a auto-similitude , c'est-à-dire l'absence de toute échelle de temps caractéristique. De plus, ayant à sa disposition un temps illimité, une marche aléatoire peut vous emmener indéfiniment loin, et de plus, elle vous conduira certainement à une distance prédéterminée par rapport à la valeur initiale! Ainsi, peu importe la qualité de vos affaires, si elles sont soumises à une errance aléatoire, elles glisseront sûrement à zéro et descendront en dessous, ce n'est qu'une question de temps! Cette loi célèbre et instructive de la vie, a reçu le nom de malédiction du joueur et son essence peut s'exprimer par une simple maxime:

La meilleure stratégie de jeu est de posséder un casino, sinon vous perdrez.

Nous ne nous attarderons pas sur ce résultat, déjà très connu, mais nous rencontrerons encore cette propriété de la marche aléatoire unidimensionnelle.

Une mémoire émotionnelle parfaite ne semble pas très bonne. Nos héros n'oublient rien et se souviennent de tout, même des événements les plus anciens! Leur humeur dans la vieillesse est affectée par le chagrin d'un jouet cassé dans l'enfance ou la joie d'un baiser dans la jeunesse. De plus, tous les baisers et jouets ultérieurs sont d'égale importance pour eux. Il faut sauver ces pauvres gens. Les émotions se calment avec le temps, le chagrin devient terne, la joie, hélas aussi. Oublier, à bien des égards, c'est comme refroidir, diffuser ou ralentir un mouvement dans un fluide visqueux, il est donc sage de le simuler de cette façon. Les processus répertoriés sont appelés processus de relaxation . Donnons à nos pauvres camarades la possibilité de se détendre!

Le système relaxant revient à l'état d'équilibre et plus vite, plus l'écart avec l'équilibre est grand. Cette propriété peut être modélisée par progression géométrique ou loi exponentielle . Nous introduisons un nouveau paramètre dans notre modèle - le taux d'oubli $$$\ mu$. Elle peut s'exprimer dans le temps (dans les lectures de notre modèle), pendant laquelle le niveau d'émotion diminuera assez fortement. Par exemple, pour $$$\ mu = 1/60$la trace émotionnelle de l'événement diminuera d'un ordre de grandeur en deux mois. Et maintenant la vie est devenue dans un bon "rayé"!

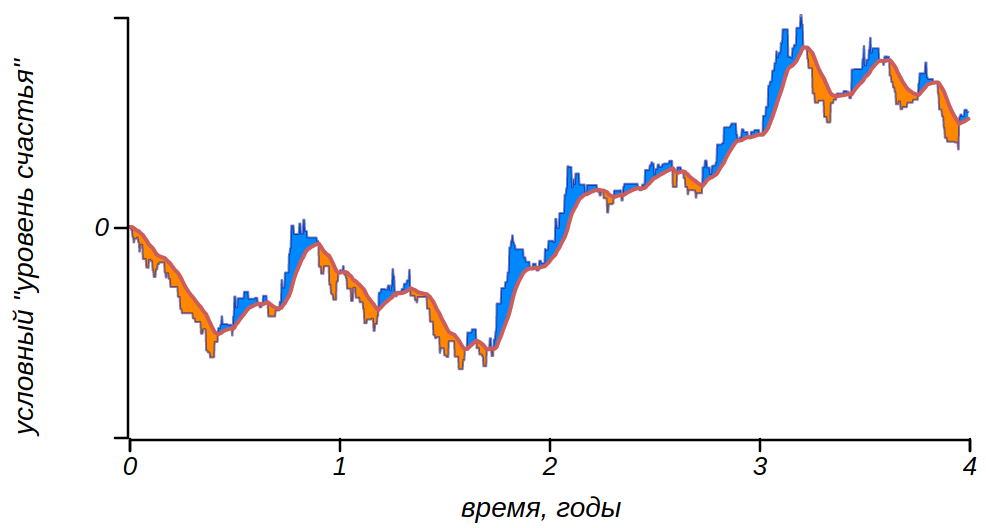
La limitation de la mémoire conduit au fait qu'une série d'événements et leurs traces de fusion de mémoire forment une série de rayures émotionnellement colorées.

En modifiant le "degré d'oubli", on peut obtenir des sujets expérimentaux plus ou moins émotionnellement équilibrés. Il semble que nous ayons trouvé une source de zèbre! Il s'agit, d'une part, de marches aléatoires, susceptibles de se propager dans toutes les directions, et d'autre part, de guérir l'oubli, de ramener l'humeur à la normale. Le résultat est une humeur sinueuse en forme de vague.

Étudions les propriétés des bandes universelles «synthétiques» que nous avons obtenues. Nous construisons un histogramme montrant la distribution de leurs durées pour une longue durée de vie (ou pour de nombreuses ordinaires) avec des paramètres $$$\ lambda = 1/7, \ quad \ mu = 1/60$.

La répartition des durées de périodes de bonheur et de chagrin pour un grand nombre de destins synthétiques. La ligne verticale marque la valeur moyenne de 33.

La première chose qui attire votre attention - la distribution maximale (mode) est proche de zéro, ce qui signifie que le plus souvent les périodes de bonheur et de malheur sont très courtes, mais il y a aussi des périodes qui durent plus d'un an. En moyenne, la durée des périodes est de 33 jours, avec un écart type de 36 jours. Cette distribution est proche de l'exponentielle (en fait, elle est bien décrite par une distribution gamma plus générale avec des paramètres qui la rapprochent de l'exponentielle). À son tour, la distribution exponentielle des durées de bande dans la vie signifie que les sautes d'humeur peuvent être considérées comme un flux de Poisson, c'est-à-dire comme une chaîne d'événements aléatoires indépendants qui n'ont pas de fréquence distincte, mais se produisent avec une intensité connue. Par exemple, dans l'exemple que nous avons examiné, les rayures sombres et claires changent avec une intensité tous les 33 jours, mais en même temps, de courtes périodes sont les plus observées dans la vie: la moitié d'entre elles ne dépassent pas dix jours.

En l’absence de «mémoire» (pour $$$\ mu = 0$), la distribution cesse d'être exponentiellement décroissante et devient exponentielle.

La distribution des durées de méandre pour une marche aléatoire a la nature d'une distribution de puissance.

Les statisticiens disent que de telles distributions ont une queue lourde , ce qui rend très probable de très grands écarts par rapport à la valeur moyenne, nous les avons observés sous la forme de longues «immersions» dans cette humeur différente. La distribution obtenue par nous a une propriété inhabituelle et étrange - ni la valeur moyenne (valeur moyenne), ni l'écart type, ni la médiane ne sont définis pour elle. Le fait est que toutes ces caractéristiques sont calculées en fonction de l'aire sous la courbe de densité de distribution, et elle est infinie. À cet égard, on peut entendre que la valeur moyenne dans ce cas est infinie, mais ce n'est pas le cas. Voyez ce qui se passe lorsque vous essayez de calculer la valeur moyenne de la durée du méandre d'une marche aléatoire:

Essayer de calculer la valeur moyenne d'une séquence de longueurs de périodes entre les sautes d'humeur en l'absence de mémoire. Les valeurs extrêmes émergentes de la queue lourde de la distribution conduisent au fait que la valeur de la moyenne ne converge vers aucune valeur.

D'énormes sauts provenant de la queue lourde abaissent continuellement la valeur moyenne et la séquence de calcul de moyenne ne converge vers aucune limite. La valeur moyenne n'est pas du tout infinie, juste l'intégrale ne converge vers aucun nombre et il est impossible de parler d'une valeur spécifique. C'est l'impossibilité de calculer la valeur moyenne de la durée du méandre qui reflète la propriété d'autosimilarité des marches aléatoires, à savoir l'absence de toute échelle de temps appropriée.

Nous avons simulé l'adaptabilité aux troubles quotidiens à l'aide de la relaxation ou de l'atténuation des explosions émotionnelles. Ce processus peut être interprété d'une autre manière, comme l'adaptabilité d'une personne aux circonstances de la vie. Lors du traitement de signaux ou de séquences bruyants, la méthode de la moyenne mobile est souvent utilisée pour lisser et extraire un signal utile, en considérant à chaque instant non pas le signal lui-même, mais la valeur moyenne du signal sur une certaine période de temps. Ainsi, il est possible de se débarrasser du bruit et de se faire une idée des tendances à long terme du signal. En appliquant une telle moyenne aux turbulences quotidiennes, nous pouvons simuler l'adaptabilité humaine. Et pendant les guerres, les gens tombent amoureux et trouvent des raisons de se réjouir, tout comme la vie des riches oisifs n'est pas sans nuages. La norme est en train de changer, à partir de laquelle l'humeur s'écarte dans un sens ou dans un autre. Compte tenu de la différence entre une séquence d'émotions et une ligne de fond lisse, nous obtenons la même image, les rayures, que le modèle précédent nous a donnée, avec les mêmes caractéristiques statistiques. Cela n'est pas surprenant, car conceptuellement, ils ne diffèrent pratiquement pas, décrivant un système avec relaxation.

Les humeurs sinueuses et changeantes peuvent être obtenues en simulant la moyenne mobile de l'adaptabilité d'une personne aux circonstances.

Connecté par une chaîne

Dans les modèles considérés, nous avons reçu un flux de Poisson de sautes d'humeur, générant des événements avec un flux de Poisson. On peut y voir du gréement - le processus aléatoire de Poisson s'est avéré être «cousu» dans le modèle. Notre résultat est-il universel? Est-il possible de l'obtenir différemment?

L'expérience du monde est une chose mal formalisée, et elle peut être adaptée à divers outils mathématiques, permettant non seulement de simplifier les hypothèses, mais aussi la spéculation. En science, cette approche est inacceptable, mais dans notre parcours à travers les méthodes de la théorie des processus aléatoires, nous pouvons nous permettre de jouer avec eux pour mieux se connaître.

En observant la dynamique de l'humeur et la perception du monde, vous pouvez voir que c'est la nature humaine de «coller» dans une certaine humeur. Si les choses vont bien dans l'ensemble, alors les mauvaises nouvelles peuvent être reçues avec optimisme. Et, au contraire, l'humeur mélancolique, une fois avalée par une personne, peut gâcher même des nouvelles joyeuses. D'un point de vue mathématique, cela signifie que la probabilité de rester dans l'humeur actuelle est supérieure à la probabilité de la changer. Ce comportement peut être décrit à l'aide d'un processus aléatoire appelé la chaîne de Markov . Dans le cas général, une chaîne de Markov peut être représentée comme un ensemble fixe d'états avec des transitions entre eux, et les transitions d'un état à l'autre ont une probabilité différente mais connue. Il est commode de représenter de telles chaînes sous forme de graphiques pondérés, par exemple, une chaîne de Markov symétrique élémentaire décrivant la dynamique de l'humeur peut être représentée de cette manière:


Chaîne de Markov avec deux états ("joyeux" et "triste"). Les flèches indiquent les transitions et les probabilités de ces transitions. Dans notre cas symétrique, la probabilité de rester dans une humeur existante dépasse la probabilité de son changement, mais ne dépend pas de l'humeur elle-même.

Notre chaîne est capable de générer des séquences d'états et, bien sûr, des bandes de zèbres du monde y apparaîtront.



Le plus intéressant est de savoir quelle distribution sera soumise à la durée de ces bandes. Pour notre modèle plus que simple, la réponse peut être exacte - il s'agit d'une distribution géométrique qui décrit la probabilité d'observer un nombre donné d'essais d'une expérience aléatoire avant d'observer le premier «succès».

Un histogramme pour les durées de périodes de la même humeur dans la séquence générée par la chaîne de Markov symétrique et la fonction de probabilité de la distribution géométrique avec un paramètre égal à la probabilité de transition entre les états. La séquence dure dix ans.

Une distribution géométrique est un analogue discret d'une distribution exponentielle, en ce sens que les valeurs arrondies d'une variable aléatoire à distribution exponentielle lui obéissent. Il existe une relation entre le paramètre de distribution géométrique et l'intensité de la distribution exponentielle correspondante. Ainsi, nous obtenons à nouveau un flux de Poisson de sautes d'humeur, et pour la chaîne de Markov que nous avons décrite, son intensité est $$$\lambda = -ln(0.75) \approx 2/7$.

Si nous brisons la symétrie de la chaîne, nous pouvons alors décrire un «optimiste» ou un «pessimiste» qui est plus disposé à «coller» dans une humeur ou une autre. La distribution des durées de bande s'écartera de la géométrie, mais en même temps, néanmoins, la plupart des bandes seront courtes. et aucune périodicité mise en évidence ne sera observée.


Un histogramme pour les durées de périodes d'humeur constante dans la séquence générée par la chaîne de Markov asymétrique. La séquence dure dix ans.

Les chaînes de Markov sont un outil puissant pour analyser les processus aléatoires dans lesquels se trouve un certain algorithme ou scénario. Ils nous donnent un aperçu particulier des processus qui sont considérés comme cycliques. Par exemple, la maxime bien connue: «l'histoire de l'humanité marche en cercle» est souvent interprétée comme le fait qu'il y a certains cycles ou même périodicités dans l'histoire. Il faut entendre, par exemple, que le début du siècle promet des bouleversements et des guerres. Au risque d'entrer dans mon propre sujet, j'oserai supposer qu'en fait il est logique de parler non pas de cycles littéraux, mais de scénarios plus ou moins stables - des chaînes régulières qui peuvent être décrites par une chaîne de Markov. Parmi les chaînes de Markov, il existe une classe de chaînes cycliques qui, en fait, sont capables de créer des séquences répétitives.Cependant, il n'y a pas de véritable périodicité déterministe dans leur comportement. Se produisant au hasard dans différentes périodes historiques et dans différents contextes, ces cycles sont similaires les uns aux autres et peuvent créer un sentiment de «déjà-vu» historique. Il est utile de les étudier et de les décrire, mais vous ne devriez peut-être pas vous attendre à un calendrier strict.

Sur ce, nous fermons le sujet du zèbre. Quelles conclusions peut-on tirer de nos recherches frivoles? Une série de rayures claires et sombres dans la vie n'est pas une illusion, elles le sont vraiment. Mais il n'y a pas de schémas particuliers en eux. Le plus souvent, ils sont courts, mais ils sont également prolongés. Tout dépend de la facilité de caractère et de la capacité de laisser aller le passé. De plus, si les événements de la vie se produisent rarement, la vie deviendra une série grise de souvenirs disparaissant dans le passé. Il est donc dans notre intérêt de se souvenir de ce qui a été vécu et il est en notre pouvoir de veiller à ce que la vie ne devienne pas une marche aléatoire. Nous pouvons faire en sorte que les bons événements s'agrandissent et se produisent plus souvent, même s'ils sont insignifiants. Un voyage de ski, un sourire sincère d'un passant, un billet de concert, une tasse de chocolat chaud par temps froid,Tout cela contribuera à créer une tendance positive et à prolonger la séquence lumineuse de la vie. Certes, la valeur moyenne suivra la tendance, de sorte que les événements tristes inévitables changeront nécessairement l'humeur. Mais ne blâmez pas votre bonheur à ce sujet. Ce n'est pas une rétribution pour lui, et pas le mauvais œil. Cette propriété des systèmes relaxants est une tendance aux oscillations lors d'une action externe stochastique.

À propos d'attendre un bus ou un tremblement de terre

La différence entre la fréquence (période) et l'intensité du flux d'événements est suffisamment importante pour être comprise lors de l'écoute des actualités ou de la lecture des résultats de la recherche scientifique. Par exemple, aujourd'hui, les sismologues, hélas, ne peuvent prédire un tremblement de terre spécifique: son heure, son lieu et sa force. Mais les méthodes de prévision sismique à long terme pour certaines régions ont été développées, mais leurs résultats sont formulés dans le langage de la théorie des probabilités, et ce qu'il faut en faire n'est pas toujours évident.

Par exemple, pour la baie d'Avachinsky, sur les rives desquelles Petropavlovsk-Kamchatsky est située en 2018, la prévision suivante a été donnée : «La probabilité totale de tremblements de terre de magnitude supérieure à 7,7, qui peut avoir une force de 7 à 9 points à Petropavlovsk-Kamchatsky, peut atteindre 52,3 pour la prochaine période de cinq ans. %. " Qu'est-ce que cela signifie?Tremblant demain? Et quand? Et où? Hélas, nous ne sommes pas encore en mesure de répondre à ces questions directes. L'interprétation exacte de ce message est la suivante: l'intensité du flux sismique est maintenant telle qu'au cours des 500 prochaines années, environ 52 tremblements de terre se produiront (en supposant que le flux reste inchangé). De plus, dans un mois, les prévisions pourraient changer. L'intensité est similaire, dans un sens, à la vitesse instantanée du mouvement: pour mesurer que vous vous déplacez à une vitesse de 60 km / h, il n'est pas nécessaire de conduire une heure entière sur les 60 km. Et, plus important encore, les prévisions faites par les scientifiques ne signifient pas que dix ans s'écoulent entre les tremblements de terre, comme on peut le supposer, divisant 500 ans en 52 événements. Ainsi, si pendant dix ans il n'y a pas eu de forts tremblements de terre, cela ne signifie pas que cela ne se produira pas aujourd'hui ou demain. Cela arrivera, bien sûr, mais combien faudra-t-il attendre,est inconnu.

Regardez comment le niveau d'activité sismique de la région du Kamchatka change à différentes échelles de temps (image prise à partir du site du moniteur d'activité sismique de la branche du Kamchatka de la Commission géophysique unifiée de l'Académie russe des sciences)


Le niveau d'activité inférieur est remplacé par un niveau plus élevé, l'activité «respire», mais pas périodiquement, mais comme la même errance aléatoire avec relaxation.

Mais les tremblements de terre, néanmoins, sont des phénomènes désagréables et ne les laissent pas se produire plus longtemps. Il y a des choses que vous attendez avec impatience, comme un bus. En arrivant à l'arrêt de bus, nous souhaitons bien sûr prendre instantanément l'itinéraire de bus ou de tramway souhaité, mais cela échoue très probablement. Ensuite, s'il y a un horaire clair à cet endroit, on le regarde, puis l'horloge, puis on se plonge dans un livre ou un téléphone. Mais souvent, au milieu de l'itinéraire, au lieu de l'horaire, l'intervalle de circulation est indiqué, par exemple, 15 minutes. Cela signifie que nous sommes déjà loin de la gare routière avec laquelle les bus partent exactement dans les délais, et une erreur s'accumule, rendant l'arrivée du bus aléatoire. Eh bien, 15, donc 15, attendons. Et ici, vous devez garder à l'esprit qu'en moyenne, vous devez attendre exactement 15 minutes, peu importe quand vous venez.Maintenant, si les bus venaient deavec une fréquence de 15 minutes, le temps d'attente moyen serait de la moitié de la période - 7,5 minutes, mais avec intensité cela ne fonctionnera pas! En l'absence de conditions supplémentaires, le mouvement des transports est modélisé par un flux de Poisson, ce qui signifie que le temps d'attente pour le bus obéira à la loi exponentielle avec la même intensité. Et l'attente mathématique pour une quantité distribuée exponentielle avec intensité$$$\lambda$ est égal $$$1/\lambda$Ainsi, notre conclusion est obtenue. Et ce qui est complètement ennuyeux - le temps que vous avez déjà passé à l'arrêt de bus n'affecte pas la probabilité que le bus soit sur le point de s'adapter. Cela fonctionne comme une propriété de la distribution exponentielle comme le manque de mémoire associé à l'indépendance des événements de Poisson.

Pour résumer. En arrivant à l'arrêt de bus, vous devez prendre une décision claire: attendez ou marchez et réfléchissez au sujet: attendez encore ou allez à pied - ne vous condamnez qu'à respecter la loi de la méchanceté. Car lorsque vous, ayant déjà attendu 17 minutes, craché et êtes parti à pied, vous serez très probablement dépassé par le bus tant attendu, voire deux. Eh bien, et pour que l'attente du bus se transforme en un concours fastidieux et désespéré avec le destin, nous rappelons la malédiction du cycliste du chapitre précédent allonge efficacement le temps d'attente observé.


Fait intéressant, la courbe de Lorentz pour la distribution exponentielle est la même pour toutes les intensités. Ainsi, l'énoncé est vrai pour tous les processus de Poisson: la moitié du temps d'observation total se produit dans 20% des cas lorsque cet événement suivant est retardé. Le coefficient de Gini pour la distribution exponentielle est exactement 1/2.

Tour extraterrestre

Je pense aux lois de la méchanceté, faisant la queue à l'aéroport pour l'enregistrement des passagers et des bagages. La file d'attente est longue, les gens sont différents et perceptibles avec tous leurs sacs, enfants ou cages. J'entends un grognement par derrière: «Comme d'habitude, notre tour est lent. Regardez, regardez, cette moustache dans une casquette était à égalité avec nous, et maintenant là-bas ... C'est la loi de la méchanceté! Mon tour est toujours lent! " Cette loi s'appelle l'observation d'Ettore:

"La ligne suivante se déplace toujours plus vite."

Il y a tout un domaine de la théorie du contrôle et de la théorie des processus aléatoires, qui traite de la dynamique des files d'attente. Ceci est important pour la conception des magasins et des salles d'attente, la gestion optimale de la salle d'opération de la banque, les portes de l'autoroute à péage et la gestion des documents. Et le point de départ pour modéliser la file d'attente est le même flux de Poisson, car il nécessite un minimum d'hypothèses supplémentaires. Ainsi, les mouvements de celui qui se tient dans la file d'attente prendront la forme d'une ligne étagée à croissance monotone, avec les mêmes étapes se produisant à des intervalles aléatoires. L'accumulation de données de cette manière s'appelle le processus de Poisson .

Voici comment deux longues lignes peuvent se déplacer:

Déplacement de deux files d'attente adjacentes en tant que processus de Poisson avec une intensité égale.

À son tour, la différence entre deux processus de Poisson identiques, à savoir qu'il est observé par une personne qui s'ennuie dans la queue, est une sorte de marche aléatoire. Et si oui, alors nous sommes prêts à tirer des conclusions. Premièrement: la distance entre les personnes se tenant simultanément dans les mêmes files d'attente augmentera ou diminuera et des méandres caractéristiques avec une durée en constante évolution se formeront. La deuxième conclusion: en raison de l'auto-similitude des marches aléatoires pour les rafales courtes et les rafales longues, les méandres auront une durée comparable au temps qu'ils font la queue, ce qui signifie qu'ils seront visibles et que les méandres seront une cause de mécontentement. Troisième conclusion: on ne sait pas à l'avance quelle file d'attente ira le plus vite, car une marche aléatoire va tout aussi bien monter que descendre. Et, enfin, la quatrième conclusion: les files d'attente se déplacent de manière indépendante, de temps en temps et se rattrapent, en moyenne, elles se déplacent de la même manière, et la différence attendue entre elles tend vers zéro, mais la répartition autour de la moyenne augmente avec le temps (dans le cas décrit par nous, la valeur le retard d'une file d'attente sur une autre est soumis à la distribution de Skellam ). Il s'avère, ou deviné avec une ligne rapide ou non - pas de méchancetés du méchant du destin!

Mais les lois de la méchanceté ne seraient pas appelées lois si elles ne revendiquaient pas l'universalité. Si nous n'avons pas la chance d'être en retard, nous y passerons plus de temps et nous aurons plus d'occasions de nous plaindre du destin! Et maintenant, attention, bonne nouvelle: dans n'importe quel intervalle de temps sélectionné, ceux qui ont la chance d'entrer dans la file d'attente rapide plus que les malchanceux, car la file d'attente rapide peut manquer plus de personnes! Mais, hélas, cela ne consolera personne coincé.

---

Le texte soumis n'a pas encore été publié, ce qui signifie qu'il peut changer. J'espère que les commentaires et remarques des lecteurs de Habr l'aideront à changer pour le mieux.