Un chapitre du livre d'Alexandre Voloshinov «Mathématiques et art» (Moscou: Lumières, 1992)
Le vénérable Pythagore a rejeté l'évaluation de la musique basée sur des preuves de sentiments. Il a soutenu que ses vertus devraient être perçues par l'esprit, et a donc jugé la musique non pas à l'oreille, mais sur la base de l'harmonie mathématique et l'a trouvée suffisante pour limiter l'étude de la musique à une octave.PlutarqueÀ proprement parler, nous parlons du système pythagoricien. Qu'est-ce que le gamma et l'échelle dans la musique?
Le gamma , ou gamme , est une séquence de sons (étapes) d'un système musical (frette), située, à partir du son principal (ton principal), dans l'ordre croissant ou décroissant. Le nom "gamma" vient de la lettre grecque Gγ (gamma), qui au Moyen Âge dénotait le ton extrême inférieur de l'échelle, puis l'échelle entière.
La caractéristique la plus importante d'un son musical est sa hauteur , qui est un reflet dans la conscience de la fréquence d'oscillation d'un corps sonore, comme une corde. Plus la fréquence d'oscillation de la corde est élevée, plus le son nous apparaît élevé.
Chaque son individuel ne forme pas un système musical et, s'il n'est pas trop fort, ne nous provoque pas beaucoup de réactions. Cependant, déjà la combinaison de deux sons dans d'autres cas s'avère agréable et harmonieuse, et dans d'autres, au contraire, elle «coupe» l'oreille. Une combinaison convenue de deux sons est appelée consonance , une combinaison incohérente est appelée dissonance . Il est clair que la consonance ou la dissonance de deux tons est déterminée par la distance d'altitude entre ces tons ou l'intervalle.
L'intervalle entre deux tons est le numéro de série de la hauteur du ton supérieur par rapport au bas de cette échelle, et le coefficient d'intervalle I 21 de deux tons est le rapport de la fréquence du ton supérieur à la fréquence du bas * :
(6.1)
* ( Dans la théorie de la musique, les concepts d'intervalle et de coefficient d'intervalle ne sont pas strictement distingués. Conformément à la tradition, nous parlons souvent de coefficient d'intervalle pour la brièveté comme un intervalle. )
Considérons maintenant un certain ensemble de sons en appuyant, par exemple, sur plusieurs touches d'un piano. Très probablement, nous obtiendrons un ensemble de sons incohérents, comme on dit, ni l'entrepôt ni la frette. Dans d'autres cas, les sons semblent s'adapter, s'entendre, mais leur combinaison semble irrégulière, inachevée. Je voudrais continuer cette séquence jusqu'à une certaine note, qui dans ce système de sons semble être la plus stable, la plus basique et appelée tonique . Ainsi, les sons dans un système musical sont interconnectés par certaines dépendances, certains d'entre eux sont instables et gravitent vers d'autres - stables .
Mais ce n'est pas seulement la tonique et la combinaison de sons stables et instables qui déterminent la nature du système musical. Il est facile de s'assurer qu'en appuyant sur huit touches blanches consécutives de la note à (échelle au naturel majeur ) et de la note a ( mineur naturel ), ces gammes sonnent différemment: la première - majeure - sonne joyeuse et légère, et la seconde - mineure - triste et couvert * . Par conséquent, il y a une autre caractéristique du système sonore - l'ambiance: majeure ou mineure. Ainsi, nous arrivons à l'un des concepts les plus complexes de la théorie de la musique - le concept de frette.
* (La nature du son de la frette, bien sûr, n'est pas définie de manière aussi grossière et sans équivoque. Cette question est très délicate, et nous en parlerons à la fin du chapitre. )
Une frette est une interaction de sons musicaux agréables à l'audition, déterminée par la dépendance des sons instables par rapport aux sons stables, et tout d'abord par le son stable principal - tonique, et ayant un certain caractère sonore - inclinaison. L'histoire de la culture musicale connaît de nombreux modes caractéristiques de peuples et d'époques différents. Les anciens Grecs connaissaient une douzaine de frettes, et les frettes de certains pays de l'Est et de l'Inde sont extrêmement complexes, particulières et inhabituelles pour l'audition européenne. Les modes modernes les plus courants se composent de sept étapes principales, chacune pouvant augmenter ou diminuer, ce qui donne cinq sons supplémentaires. Ainsi, la frette gamma diatonique (7 étapes) se transforme en chromatique (12 sons). La première étape de la frette est le tonique. Les lois de la structure de la frette sont toute une science, pierre angulaire de la musicologie, et de nombreux scientifiques et compositeurs ont consacré leur vie entière à l'étude de ces lois.
Nous nous intéresserons principalement aux lois mathématiques qui décrivent la structure de la frette, c'est-à-dire le système musical. Le système musical est l'expression mathématique d'un certain système de relations de hauteur. En plus d'un intérêt purement théorique, le système trouve une application dans l'accordage d'instruments de musique avec une hauteur de son fixe, comme un piano ou un orgue.
En conclusion, nous constatons que nos expériences avec l'appui sur les touches du piano peuvent se terminer avec le phénomène le plus rare et le plus agréable, quand le système de son pris n'appartiendra pas seulement à une frette, mais aura également un sens. Une telle série séquentielle de sons de sens artistique de différentes hauteurs est appelée mélodie . C'est juste ce que nous aimons fredonner en fonction de notre humeur - énergique, triste, joyeux ...
Après une si courte excursion dans la musicologie théorique, nous pouvons retourner sur les rives des Hellas ensoleillées à l'époque du sage Pythagore. Nous allons essayer de restaurer le raisonnement de Pythagore et de ses élèves lors de la construction du système pythagoricien, car c'est ce système qui a déterminé pendant des millénaires, sinon pour toujours, tout le développement de la culture musicale, non seulement européenne, mais aussi orientale. Pythagore lui-même n'a laissé aucune œuvre écrite, et l'héritage des Pythagoriciens semble être un tas de ruines sans espoir, c'est-à-dire une collection de fragments survivant accidentellement et de citations ultérieures. Sans aucun doute, ces ruines sont belles et étonnent toujours l'imagination, comme les ruines du célèbre Parthénon, mais une grande partie de ces fragments sont complètement perdus et vous ne pouvez souvent que deviner l'ensemble. Et pourtant ...
Monochord - single-string - a été l'un des premiers instruments de musique des anciens Grecs. C'était une longue boîte nécessaire pour amplifier le son sur lequel la corde était tirée. Par le bas, la corde a été tirée par un support mobile pour diviser la corde en deux parties sonnant séparément. Sur une boîte en bois sous la corde, il y avait une échelle de divisions, ce qui a permis de déterminer avec précision quelle partie de la corde sonne. Bien sûr, en tant qu'instrument de musique, le monocorde nous semblera trop primitif, mais c'était un excellent instrument physique et un outil pédagogique sur lequel les contemplateurs anciens ont compris la sagesse de l'alphabétisation musicale.
Les anciens affirmaient que Pythagore connaissait déjà les lois de vibration de la corde de monocorde et la construction des consonances musicales (consonances), cependant, nous trouvons un enregistrement de ces lois de l'archite pythagoricienne de Tarente (428-365 avant JC), qui a vécu un siècle et demi plus tard que Pythagore . L'architecte était, bien sûr, le représentant le plus éminent de l'école de Pythagore, un ami du philosophe Platon et professeur du mathématicien Eudoxe (vers 408 - vers 355 avant JC), homme d'État et commandant. La polyvalence d'Architus est incroyable: il a résolu le fameux problème de los de doubler le cube, était à juste titre considéré comme le plus grand théoricien de la musique pythagoricienne, le premier à rationaliser la mécanique basée sur les mathématiques et à réduire les mouvements des mécanismes en dessins géométriques, travailler sur un modèle en bois d'une colombe volante. Selon Van der Waerden, Arch est l'auteur du VIII livre "Les débuts" d'Euclide, qui expose la théorie arithmétique des proportions. En tant qu'homme d'État, Archit était extrêmement respecté: il a été élu stratège sept ans de suite * , bien que, selon la loi, les stratèges n'aient été choisis que pour un an. Grâce à des manœuvres diplomatiques habiles, l'architecte a sauvé Platon de la captivité et a ainsi sauvé la vie du grand philosophe. "Architectes glorieux, terres et mers, et calculatrice de sable ..." - a écrit Horace.
* ( Stratège - dans les anciennes cités grecques, un chef militaire doté de pouvoirs militaires et politiques chi-ki. )
Les "Lois de Pythagore-Archite", sur lesquelles toute la théorie pythagoricienne de la musique était basée, peuvent être formulées comme suit:
1- La hauteur (fréquence d'oscillation f) de la corde sonore est inversement proportionnelle à sa longueur l:
(6.2)
ici a est le coefficient de proportionnalité, en fonction des propriétés physiques de la corde (épaisseur, matière, etc.).
2. Deux chaînes sonores ne donnent une consonance que lorsque leurs longueurs sont appelées entiers constituant le nombre triangulaire 10 = 1 + 2 + 3 + 4, c'est-à-dire 1: 2, 2: 3, 3: 4.
Ces intervalles sont des «consonances parfaites», et leurs coefficients d'intervalle ont reçu plus tard les noms latins * :
* ( Les noms des intervalles dans la musique sont des chiffres latins, qui indiquent le numéro de série de l'échelle de l'échelle constituant l'intervalle avec la phase initiale: octave - huitième, cinquième - cinquième, quatrième - quatrième, etc. )
octave
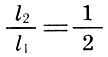
quint
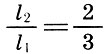
quart
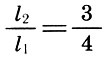
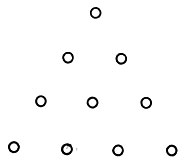
Numéro triangulaire 10
Il a également été noté que la fusion la plus complète des tons est donnée par une octave (2/1), suivie par une quint (3/2) et un quart (4/3), c'est-à-dire plus le nombre n est petit par rapport à la forme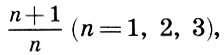 
plus l'intervalle est cohérent.
"La deuxième loi de Pythagore - Archite" et semble maintenant surprenant. Que dire des Pythagoriciens, qu'il a tout simplement captivés! Ici, ils ont trouvé la confirmation de toute leur philosophie: les nombres entiers, d'ailleurs, les nombres tetraktis gouvernent tout, même la musique! Les Pythagoriciens ne se sont pas fait attendre longtemps et ont étendu la loi des relations musicales autant que possible, y compris la structure de l'univers.
Donc, si nous prenons le segment l égal à 1/12 de la longueur de la chaîne de monocorde l 1 comme prix de division de l'échelle de monocorde, alors avec l'ensemble de la chaîne de monocorde de longueur l 1 = 12l, ses parties de longueur l 2 = 6l seront conformes - le son est une octave plus haut (l 2 / l 1 = l / 2), l 3 = 9l - sonner un quint plus haut (l 3 / l 1 = 2/3) et l 4 = 8l - sonner un quart plus haut (l 4 / l 1 = 3/4 ) Cette consonance et ses nombres définissant 6, 8, 9, 12 étaient appelés tétrade (quatre). Les Pythagoriciens croyaient que la tétrade était "cette échelle selon laquelle les sirènes chantent". Lors de l'accordage de l'ancienne lyre, qui est devenue le symbole de la musique, ses quatre cordes étaient nécessairement accordées selon la règle de la tétrade, et l'accord des cordes restantes dépendait de la frette dans laquelle la jouer.
Mais pour l'ancien penseur, il ne suffisait pas d'établir les valeurs numériques des quantités étudiées. L'œil et l'esprit pythagoriciens sont habitués non seulement à mesurer, mais aussi à mesurer, c'est-à-dire à révéler les liens internes entre les sujets étudiés, c'est-à-dire à établir des relations proportionnelles. L'architecte était un vrai pythagoricien et il a établi des relations proportionnelles entre la consonance parfaite principale - une octave, une cinquième et une quatrième. Cette décision a été obtenue par les architectes dans le cadre du désir de diviser l'octave en intervalles harmonieux. Arch est probablement basé sur l'hypothèse intuitivement évidente qui, avec les tons f 1 et f 2 = 2f 1 , donne la consonance principale - une octave, la consonance et leur moyenne arithmétique f 3 = (f 1 + f 2 ) / 2 devraient donner. Mais alors la longueur de chaîne l 3 sera exprimée en termes de longueurs de chaîne l 1 et l 2 selon (6.2) comme suit:
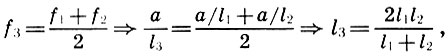
c'est-à-dire que l 3 est la moyenne harmonique l 1 et l 2 (voir 5.1). L'inverse est également facile à détecter: la moyenne harmonique pour les fréquences f 1 et f 2 va dans la moyenne arithmétique pour les longueurs l 1 et l 2 :
Se souvenir que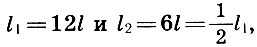 
Avec les architectes, nous arrivons à une conclusion importante:
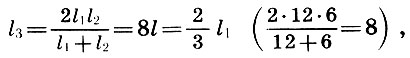
(6.3)
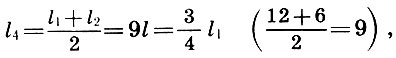
(6.4)
c'est-à-dire que le cinquième est la moyenne harmonique des longueurs des cordes du ton fondamental l 1 et des octaves l 2 , et le quart est la moyenne arithmétique de l 1 et l 2 .
Mais le produit de la moyenne arithmétique et de la moyenne harmonique est égal au produit des nombres originaux:
(6.5)
d'où, en divisant les deux parties par l 1 2 , on obtient la deuxième conclusion importante:
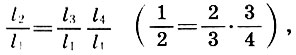
(6.6)
ou
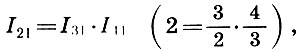
c'est-à-dire qu'une octave est le produit d'un cinquième à un quart.
Divisant (6,5) par l 1 l 3 , Archite obtient le tiers des proportions principales - géométrique:
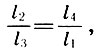
(6.7)
qui s'appelait "musical": une octave se rapporte à une quint autant qu'un quart à un ton fondamental .
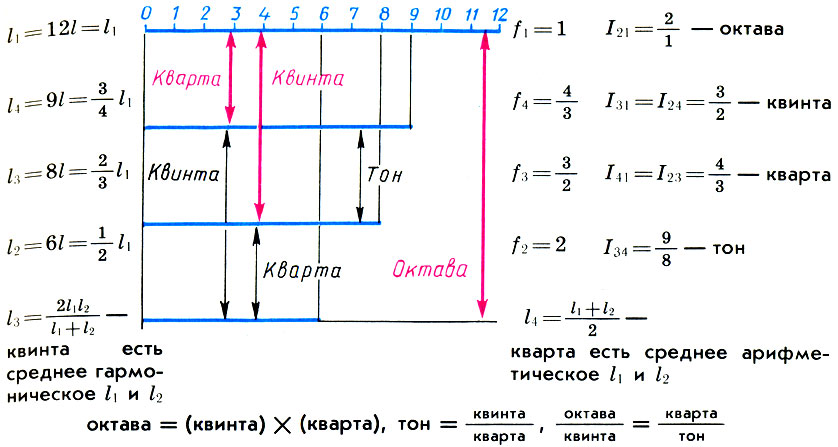
Division d'une corde de monocorde (l 1 ) en parties qui forment des consonances parfaites avec elle: une octave (l 2 ), une cinquième (l 3 ) et un quart (l 4 ) et les relations entre elles. Les intervalles que forme une chaîne entière de monocorde avec ses parties sont indiqués par des flèches rouges
Il est facile d'obtenir deux relations supplémentaires:
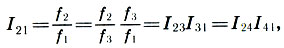
(6.8)
c'est-à-dire que l' octave est divisée en deux intervalles de consonnes inégales - le cinquième et le quatrième . Un intervalle qui étend cet intervalle à une octave est appelé son inversion . Ainsi, le quint est l'inverse du quart et vice versa.
Enfin, nous trouvons le coefficient d'intervalle entre les cordes de la quinte l 3 et du quart l 4 , qui avec son intervalle est appelé le ton (ne confondez pas l'intervalle de ton et le son de ton d'une hauteur donnée):
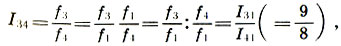
(6,9)
c'est-à-dire que l' intervalle de tonalité est égal au rapport du cinquième au quatrième .
Notez que, contrairement à la distance habituelle sur la droite r 21 = x 2 - x 1 définie comme la différence entre les coordonnées de la fin et du début, le coefficient d'intervalle - la distance d'altitude - est défini comme le rapport de ses tons constitutifs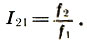 
Puis trois tons f 1 <f 2 <f 3 situés à égale distance r et formant une progression arithmétique x 1 , x 2 = x 1 + r, x 3 = x 1 + 2r. Par conséquent, les coefficients d'intervalle sont ajoutés et soustraits «géométriquement», et les intervalles eux-mêmes - «arithmétiquement», comme les distances habituelles, à savoir:
la somme de deux intervalles est égale au produit de leurs coefficients d'intervalle:
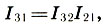
(6.10)
la différence de deux intervalles est égale au quotient de leurs coefficients d'intervalle:
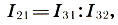
(6.11)
diviser l'intervalle en n parties égales signifie extraire une racine de degré n de son coefficient d'intervalle:
(6.12)
etc.
Pour passer des coefficients d'intervalle aux intervalles de distance, il suffit d'introduire l'intervalle logarithmique L = log a I et la fréquence logarithmique F = log a f. Ensuite, le logarithme de la définition (6.1) et des égalités (6.10) - (6.12) nous obtenons la définition et les règles d'action habituelles avec les distances:
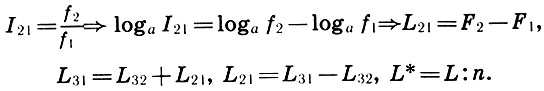
(6.13)
La solution du problème de la division d'octave a immédiatement incité Archit à prouver l'irrationalité 
. En fait, si nous essayons de diviser l'octave en deux intervalles égaux I, alors, en mettant (6.8) I 23 = I 31 = I, nous avons
Mais avec ce rapport de longueurs de cordes, une nette dissonance se fait entendre. Puisque la consonance est déterminée par le rapport des entiers de la forme (n + 1): 2, l'idée suggère que le nombre ne peut pas être exprimé par le rapport de deux entiers, c'est-à-dire qu'il est irrationnel.
La deuxième preuve d'irrationalité moins musical, mais plus mathématique. Pour trouver la racine carrée d'un nombre qui n'est pas un carré complet, Archit le décompose en deux facteurs inégaux (2 = 1 * 2), puis forme la moyenne arithmétique 3/2 et la moyenne harmonique 4/3 à partir de ces facteurs et compose une proportion musicale à partir de ces nombres ( 6.7):
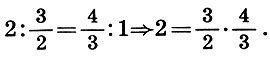
Le produit des termes moyens de cette proportion est égal à un nombre donné 2, et leur différence 
inférieure à la différence de l'approximation zéro 2 - 1 = 1. Par conséquent, 
peut être considéré comme des valeurs approximatives .
(3/2 avec excès, 4/3 avec carence].
Après avoir fait la même procédure sur les premières approximations, nous obtenons les secondes approximations:
en plus
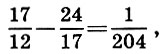
puis les troisièmes approximations:
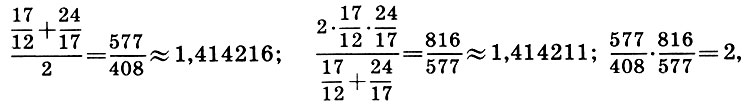
en plus
1,414216-1,414211 = 0,000005.
Cette procédure pouvant être répétée indéfiniment, il est clair que le nombre irrationnel. En chemin, nous sommes convaincus de la justesse de l'idée pythagoricienne selon laquelle plus les entiers sont grands dans la relation, plus ils expriment avec précision le nombre irrationnel (voir p. 96). Enfin, en se souvenant de ce sens est égal à 1,414213 ..., on voit que la méthode "musicale" d'Archit converge très rapidement vers la valeur exacte et déjà la troisième approximation donne cinq décimales correctes!
Mais revenons à nos intervalles. Ainsi, l'octave est divisée en deux consonances inégales des cinquième et quatrième, et la cinquième - par la quatrième et la dissonance. L'intervalle de ton a été pris comme l'intervalle entre les sons voisins (étapes) en hauteur lors de la construction de l'échelle pythagoricienne. Voici la clé de la construction d'une frette. Selon le musicologue soviétique L. A. Mazel, l'intervalle du cinquième, divisé en quart et ton, est le principal élément musical. En choisissant le ton comme mode principal de formation, les anciens théoriciens n'ont qu'à mettre de côté le son principal 
puis un autre ton 
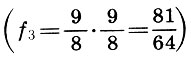et l'intervalle restant entre le deuxième ton et le quart de ton 
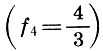demi - teinte d' appel 
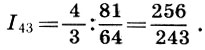Ce nom est tout à fait justifié, car la division de l'intervalle de tonalité en deux selon la formule (6.12) donne 
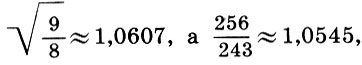c'est-à-dire qu'un demi-ton est presque égal à un demi-ton * . Ainsi a été obtenue la base de toute la musique grecque antique - le tétrachord - une gamme à quatre cordes dans un quart.
* (L' intervalle de ton (demi-teinte) en théorie musicale est accepté comme une unité de mesure arithmétique des intervalles, et les intervalles de ton et de demi-teinte, contrairement à leurs coefficients d'intervalle, sont appelés grandes et petites secondes. )
Il est clair qu'il n'y a que trois possibilités pour la position du demi-ton dans le tétrachord, qui a déterminé la nature et le nom du tétrachord:
Dorian: demi - teinte - ton - ton;
Phrygien: ton - demi -ton - ton;
Lydian: ton - ton - demi - ton .
Les noms des tétrachords indiquent les régions respectives de la Grèce et de l'Asie Mineure, chacune chantant dans sa propre harmonie.
Bien sûr, quatre cordes dans un quart n'étaient pas suffisantes pour diriger la mélodie, donc les tétracordes étaient connectés. Nous avons déjà découvert qu'une octave se compose de deux quarts et d'un ton; , , . , , «». «» — . :
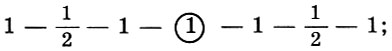
1 , 1/2 — , . . , , , (2 — , 3 — , - - - - - - c - o ), — * .
* ( «» , (1 — 1/2 — 1 — 1 — 1/2 — 1 — 1) , — . )
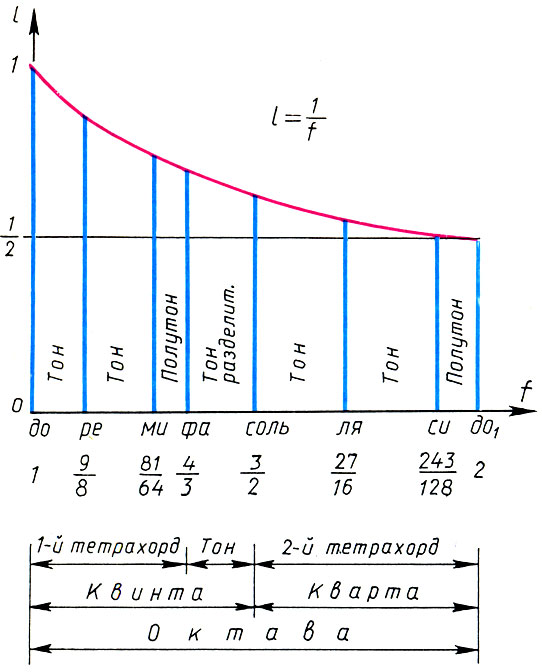Système de Pythagore de la gamme lydienne et ses caractéristiques mathématiques, , , , , . . . f 1 = 1, o : f 1 = 1, f 2 = 9 / 8 , f 3 = 9 / 8 * 9 / 8 = 81 / 64 , f 4 = 4 / 3 . : f 5 = 3 / 2f L = 3 / 2 , f 6 = 3 / 2 f 2 = 27 / 16 , f 7 = 3 / 2 f 3 = 243 / 128 , f 8 = 3 / 2 f 4 = 2. Enfin, nous avons pour les coefficients d' intervalle
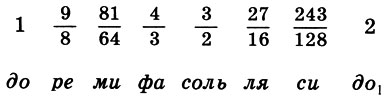(6.14)Ceci est le canon de Pythagore. Selon la légende, le canon de Pythagore a d'abord trouvé une application pratique dans le réglage de la lyre du légendaire Orphée.
. «» , . . , -(-), — - (-). 6 , (- — — ) . , . , , . , , . 1 , , , , — , . .
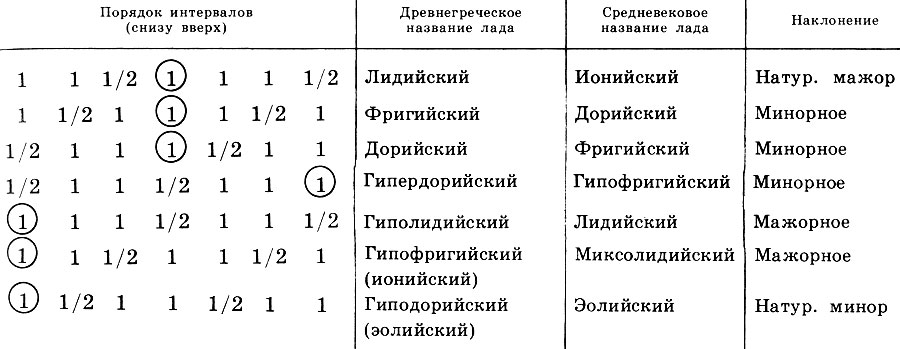Tableau 1. La séquence d'intervalles de tons (1) et de demi-tons (1/2) dans les frettes anciennes (de bas en haut), les noms grecs et médiévaux des frettes et leur inclinaisonSi l'on se souvient qu'à présent seules deux frettes dominent - majeure et mineure, on ne peut que se demander à quel point l'ancienne conscience musicale était sophistiquée. Les Grecs remplissaient dans chaque sens un certain contenu éthique et esthétique, son «ethos», établissant un lien clair entre les images musicales et les états de l'âme. Des fonctions magiques et même médicales sont attribuées à la musique, mais une importance particulière est attachée à la musique comme moyen d'éducation.
Menada dansante. Soulagement, «» , . , , ,- (. 551-479 . . .), : « , — ». , , , . , , , , . , , , . , . , , . , , «» , , , , .
Aristote en politique juge les frettes, peut-être même plus strictes que Platon, ne reconnaissant que le mode dorien comme un mode capable d'entraîner la psyché. Néanmoins, Aristote fait une classification "éthique" détaillée des modes, distinguant les modes qui provoquent l'équilibre mental (dorien), au contraire, le violent (hypofrigian - mode "table"), stimulent la volonté et le désir d'action (hypodorien - mode de la tragédie grecque), provoquer un état extatique et extatique (Phrygien, hypolidien).
Nous trouvons une belle description de l '«éthos» des frettes grecques dans le livre de l'ancien écrivain romain Apulée (vers 124 -?) «Florids»: «Il y avait un flûtiste du nom d'Antigenides. Chaque son de ce jeu de musicien était doux, toutes les frettes lui étaient familières, et il pouvait recréer pour vous, selon votre choix, la simplicité de la frette éolienne, la richesse de l'ionien, la tristesse du lydien, l'exaltation du phrygien et le militantisme de Doria.
Mais arrêtez! Y a-t-il une contradiction ici? L'humeur dorienne est appelée belligérante, mais en fait c'est en fait notre mineur! Étant donné que c'était l'humeur dorienne qui était considérée comme vraiment grecque, il s'avère que le personnage principal de la musique grecque est triste, mineur. Pour les Grecs, l'humeur dorienne est l'expression de la vivacité, de la gaieté et même du militantisme. C'est ainsi que l'éminent érudit contemporain de l'Antiquité, dernier philosophe de «l'âge d'argent» russe, le professeur A. F. Losev (1893-1988) * explique: «L'art grec est une affirmation de vie invariable». La retenue noble et même la tristesse ne quittent pas le Grec même quand il s'amuse, quand il construit joyeusement sa vie, quand il est en guerre et en train de mourir. Les «joyeux» frettes d'une manière ou d'une autre gravitent vers ce deuil beau, noble, vigoureux, important et en même temps majestueusement triste - Dorian. L'ambiance dorienne est le style sculptural de la musique grecque ... Donc, toute la sculpture grecque est si réfléchie, triste et noble. "
* ( Le sort d'Aleksei Fedorovich Losev est heureux et tragique. Il est heureux parce que jusqu'au dernier jour de sa vie de 95 ans, Losev a conservé une capacité de travail incroyable et a réussi à terminer le travail principal - les huit volumes "Histoire de l'esthétique ancienne". Tragique, parce que les huit autres volumes de ses œuvres sont écrits un demi-siècle plus tôt (1927 - 1930), ils étaient anathématisés, et l'auteur lui-même, illégalement réprimé, a poursuivi ses recherches philosophiques sur la construction du canal Mer Blanche-Baltique, d'où il écrivait: «Je suis enchaîné quand mon âme bouillonne forces éternelles et inépuisables. "L'une de ces œuvres de Losev," La musique comme sujet de logique ", pourrait servir de guide à ce livre. Néanmoins, le sort de A.F. Losev est heureux, car les manuscrits ne brûlent pas. Aujourd'hui, le grand héritage philosophique de A F. Losev retrouve sa renaissance. )
Mais qu'en est-il de la manière lydienne? Après tout, c'est exactement notre majeur, alors qu'Apuleius l'appelle triste et Platon - les funérailles! Eh bien, en évaluant la frette Lydian, Aristote n'était pas d'accord avec Platon, trouvant une puérilité et un charme naïf dans la frette Lydian et l'attribuant à des frettes qui provoquent l'équilibre mental. Au fil du temps, le mode lydien a perdu son caractère déplorable, et les anciens théoriciens ont commencé à parler plus souvent de la "douce mélodie lydienne" ou de la "mélodie lydienne diversifiée".
Ainsi, nous voyons que la question de l '«éthos» des frettes n'est pas résolue sans ambiguïté et est largement déterminée par la tradition d'appliquer telle ou telle frette. Et à notre époque, l'auditeur, élevé par exemple dans une musique indienne subtile et particulière, ne fait pas de distinction entre le majeur et le mineur, sans parler de leur «ethos». Bien sûr, l'ambiance principale se distingue par des tons plus légers et plus joyeux, et il y a des raisons objectives à cela, que nous discuterons au chapitre 10. Mais la réalisation de ces possibilités dépend d'une multitude d'autres facteurs (tempo, rythme, motif mélodique, etc.), et donc il y a beaucoup d'œuvres gaies et énergiques en mineur et triste, couvant en majeur. Rappelons au moins la «Sonate Pathétique» en mineur Beethoven, ce monologue fougueux et passionné du Héros, appelant à une bataille acharnée et même à la mort. De nombreux artistes ont ramassé de nombreuses épithètes pour cette sonate (bien que, peut-être, la meilleure - pathétique - appartient à Beethoven lui-même), mais elle ne peut pas être qualifiée de triste seulement - mineure. Au contraire, Nocturne n ° 2 op. Le 9e bémol majeur de Chopin est imprégné d'une douce rêverie. Ce sont des souvenirs tristes et flous de l'auteur, mais en aucun cas une pièce joyeuse - majeure -. En conclusion, essayons de dire quelques mots sur "l'éthos des intervalles", car le présent chapitre est consacré à l'analyse des intervalles musicaux. Nous allons essayer, car cette question est encore plus controversée et peu développée que «l'éthique des frettes». Et pourtant ...
Jusqu'à présent, nous n'avons rien dit sur la «consonance la plus parfaite» - prima (unisson) (l 2 / l 1 = 1, c'est-à-dire que deux cordes produisent un son de la même hauteur), car du point de vue des mathématiques cet intervalle n'a pas d'intérêt. Cependant, dans l'orchestre, cet intervalle le plus simple joue un rôle énorme, donnant ce volume sonore et cette luminosité.
La prochaine consonance parfaite est l'octave. En même temps, l'octave donne également l'impression d'un son tridimensionnel, et avec un son séquentiel, une sensation d'espace et de largeur. Une excellente illustration de cela est le «Chant de la patrie» du compositeur I. O. Dunaevsky (1900-1955). Dans son chœur ("De Moscou à la périphérie ..."), une octave ascendante (l 1 / l 2 = 2) sonne deux fois, peignant les vastes étendues de notre Patrie. Ici, après deux octaves, il y a une cinquième ascendante. Une quinta (l 1 / l 2 = 3/2) sonne aussi large, mais plus texturée et dynamique qu'une octave.
Les mélodies de nombreuses chansons et hymnes révolutionnaires commencent par un intervalle d'un quart ascendant (l 1 / l 2 = 4/3), par exemple, International, Hymne de l'Union soviétique, Marseillaise. Ici, l'intervalle d'un quart sonne résolument et activement, comme un appel à l'action.
Il y a un «ethos» spécial dans l'intervalle d'une seconde: avec un son simultané, il est dissonant et désagréable, mais avec un son successif le précédent déborde dans le suivant, formant le flux naturel de la mélodie d'un son à l'autre. Dans une mélodie, les intervalles entre deux sons de référence sont souvent remplis en deuxièmes intervalles consécutifs. Par exemple, la chanson «A Birch Stood in the Field» commence par un cinquième intervalle rempli de secondes consécutives, qui donne l'impression d'un flux calme et majestueux de la mélodie, comme des images majestueuses et calmes de la nature russe.
Et le plus désagréable et dissonant est l'intervalle triton ou semi-octave (l 1 / l 2 = ) Par son incohérence, cet intervalle «a incité» l'Archite à une «preuve musicale» d'irrationalité .
Merci à la Library of Mathematics d' avoir numérisé le livre.