Richard Hamming: Chapitre 10. Théorie du codage - I

«Le but de ce cours est de vous préparer à votre avenir technique.»

Salut, Habr. Vous vous souvenez de l'article génial "Vous et votre travail" (+219, 2442 signets, 394k lectures)?

Hamming (oui, oui, les codes Hamming à vérification automatique et à correction automatique) a un livre entier écrit sur la base de ses conférences. Nous le traduisons, parce que l'homme parle d'affaires.

Ce livre n'est pas seulement sur l'informatique, c'est un livre sur le style de pensée des gens incroyablement cool. «Ce n'est pas seulement une charge de pensée positive; il décrit les conditions qui augmentent les chances de faire du bon travail. »

Nous avons déjà traduit 28 chapitres (sur 30). Et nous travaillons sur une édition papier.

Théorie du codage - I

Après avoir considéré les ordinateurs et le principe de leur travail, nous allons maintenant considérer la question de l'information: comment les ordinateurs représentent l'information que nous voulons traiter. La signification de n'importe quel caractère peut dépendre de la façon dont il est traité, la machine n'a pas de signification spécifique pour le bit utilisé. En discutant de l'histoire du logiciel, chapitre 4, nous avons considéré un langage de programmation synthétique, dans lequel le code de l'instruction break coïncidait avec le code d'autres instructions. Cette situation est typique de la plupart des langues, la signification de l'instruction est déterminée par le programme correspondant.

Pour simplifier le problème de la présentation d'informations, nous considérons le problème de la transmission d'informations d'un point à un autre. Cette question est liée à la question des informations sur la conservation. Les problèmes de transmission d'informations dans le temps et dans l'espace sont identiques. La figure 10.1 montre un modèle standard de transmission d'informations.



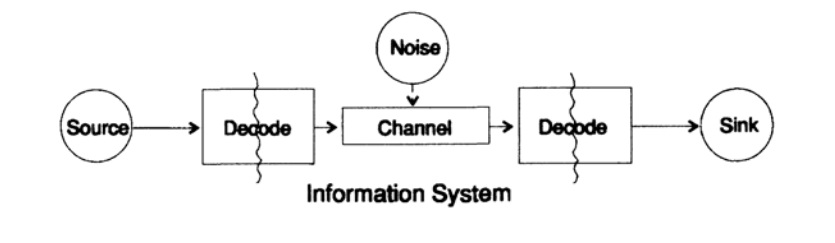Figure 10.1

À gauche sur la figure 10.1 se trouve la source d'informations. Lorsque nous considérons le modèle, nous ne nous soucions pas de la nature de la source. Il peut s'agir d'un ensemble de symboles de l'alphabet, de nombres, de formules mathématiques, de notes de musique, de symboles avec lesquels nous pouvons représenter des mouvements de danse - la nature de la source et la signification des symboles qui y sont stockés ne font pas partie du modèle de transmission. Nous ne considérons que la source d'information, avec une telle restriction, nous obtenons une théorie générale puissante qui peut être étendue à de nombreux domaines. Il s'agit d'une abstraction de nombreuses applications.

Lorsque Shannon a créé la théorie de l'information à la fin des années 40, on pensait qu'elle devrait s'appeler la théorie de la communication, mais il a insisté sur le terme information. Ce terme est devenu une cause constante à la fois d'un intérêt accru et d'une déception constante en théorie. Les enquêteurs ont voulu construire des «théories de l'information» entières, elles ont dégénéré en une théorie d'un ensemble de personnages. Revenant au modèle de transmission, nous avons une source de données qui doit être codée pour la transmission.

L'encodeur se compose de deux parties, la première partie est appelée l'encodeur source, le nom exact dépend du type de source. Les sources de différents types de données correspondent à différents types de codeurs.

La deuxième partie du processus de codage est appelée codage de canal et dépend du type de canal pour la transmission de données. Ainsi, la deuxième partie du processus de codage est cohérente avec le type de canal de transmission. Ainsi, lors de l'utilisation d'interfaces standard, les données de la source sont initialement codées selon les exigences de l'interface, puis selon les exigences du canal de données utilisé.

Selon le modèle de la figure 10.1, le canal de données est exposé à un «bruit aléatoire supplémentaire». À ce stade, tout le bruit dans le système est combiné. Il est supposé que le codeur accepte tous les caractères sans distorsion et que le décodeur remplit sa fonction sans erreur. Il s'agit d'une certaine idéalisation, mais à de nombreuses fins pratiques, elle est proche de la réalité.

La phase de décodage comprend également deux étapes: canal - standard, standard - récepteur de données. À la fin du transfert de données est transmis au consommateur. Et encore une fois, nous ne considérons pas comment le consommateur interprète ces données.

Comme indiqué précédemment, un système de transmission de données, par exemple des messages téléphoniques, radio, programmes de télévision, présente des données sous la forme d'un ensemble de nombres dans les registres d'un ordinateur. Je le répète, la transmission dans l'espace n'est pas différente de la transmission dans le temps ou du stockage d'informations. Avez-vous des informations qui seront nécessaires après un certain temps, alors elles doivent être encodées et stockées sur la source de stockage des données. Si nécessaire, les informations sont décodées. Si le système de codage et de décodage est le même, nous transmettons les données via le canal de transmission sans modifications.

La différence fondamentale entre la théorie présentée et la théorie habituelle en physique est l'hypothèse qu'il n'y a pas de bruit dans la source et le récepteur. En fait, des erreurs se produisent dans n'importe quel équipement. En mécanique quantique, le bruit se produit à n'importe quel stade selon le principe d'incertitude, et non comme une condition initiale; en tout cas, le concept de bruit en théorie de l'information n'est pas équivalent à un concept similaire en mécanique quantique.
Pour plus de précision, nous examinerons en outre la forme binaire de représentation des données dans le système. Les autres formulaires sont traités de manière similaire, par souci de simplicité, nous ne les considérerons pas.

Nous commençons notre examen des systèmes avec des caractères codés de longueur variable, comme dans le code Morse classique de points et de tirets, dans lequel les caractères fréquents sont courts et les caractères rares sont longs. Cette approche vous permet d'obtenir une efficacité élevée du code, mais il convient de noter que le code Morse est ternaire, pas binaire, car il contient un espace entre les points et les tirets. Si tous les caractères du code ont la même longueur, un tel code est appelé code de bloc.

La première propriété nécessaire évidente du code est la capacité de décoder de manière unique le message en l'absence de bruit, du moins cela semble être la propriété souhaitée, bien que dans certaines situations cette exigence puisse être négligée. Les données du canal de transmission pour le récepteur ressemblent à un flux de caractères provenant de zéros et de uns.

Nous appellerons deux caractères adjacents une double extension, trois caractères adjacents une triple extension, et dans le cas général, si nous transmettons N caractères, le récepteur voit des ajouts au code de base de N caractères. Le récepteur, ne connaissant pas la valeur de N, doit diviser le flux en blocs de diffusion. Ou, en d'autres termes, le récepteur devrait être en mesure de décomposer le flux de manière unique afin de restaurer le message d'origine.

Considérez un alphabet d'un petit nombre de caractères, généralement les alphabets sont beaucoup plus grands. Les alphabets des langues commencent de 16 à 36 caractères, y compris les majuscules et les minuscules, les signes numériques, la ponctuation. Par exemple, dans la table ASCII 128 = 2 ^ 7 caractères.
Considérons un code spécial composé de 4 caractères s1, s2, s3, s4

s1 = 0; s2 = 00; s3 = 01; s4 = 11.

Comment le récepteur doit-il interpréter la prochaine expression reçue

0011 ?

Comment s1s1s4 ou comment s2s4 ?

Vous ne pouvez pas répondre sans ambiguïté à cette question, ce code n'est certainement pas décodé, il n'est donc pas satisfaisant. Code, d'autre part

s1 = 0; s2 = 10; s3 = 110; s4 = 111

décode le message d'une manière unique. Prenez une chaîne arbitraire et réfléchissez à la façon dont le récepteur la décodera. Vous devez construire un arbre de décodage selon le formulaire de la figure 10.II. String

1101000010011011100010100110 ...

peut être divisé en blocs de caractères

110, 10, 0, 10, 0, 110, 111, 0, 0, 0, 10, 10, 0, 110, ...

selon la règle suivante pour construire un arbre de décodage:

Si vous êtes au sommet de l'arborescence, lisez le caractère suivant. Lorsque vous atteignez une feuille d'un arbre, vous convertissez la séquence en personnage et revenez au début.

La raison de l'existence d'un tel arbre est qu'aucun caractère n'est un préfixe de l'autre, vous savez donc toujours quand vous devez revenir au début de l'arbre de décodage.

Il est nécessaire de faire attention aux points suivants. Premièrement, le décodage est un processus strictement en flux, dans lequel chaque bit n'est examiné qu'une seule fois. Deuxièmement, les protocoles incluent généralement des caractères qui marquent la fin du processus de décodage et sont nécessaires pour indiquer la fin d'un message.

Le fait de ne pas utiliser de caractère de fin est une erreur courante dans la conception du code. Bien sûr, vous pouvez fournir un mode de décodage constant, auquel cas le caractère de fin n'est pas nécessaire.



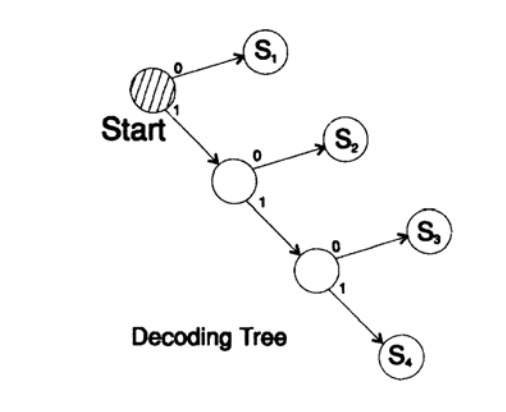Figure 10.II

La question suivante concerne les codes de décodage (instantané) de flux. Considérez le code obtenu à partir du précédent en affichant des caractères

s1 = 0; s2 = 01; s3 = 011; s4 = 111.

Supposons que nous obtenions la séquence 011111 ... 111 . La seule façon de décoder le texte du message est de regrouper les bits de la fin de 3 en un groupe et de sélectionner des groupes avec un zéro devant devant ceux-ci, après quoi vous pouvez décoder. Un tel code est décodé d'une manière unique, mais pas instantanément! Pour le décodage, vous devez attendre la fin du transfert! En pratique, cette approche élimine le taux de décodage (théorème de Macmillan), il est donc nécessaire de rechercher des méthodes de décodage instantané.

Considérez deux façons de coder le même caractère, Si:

s1 = 0; s2 = 10; s3 = 110; s4 = 1110, s5 = 1111,

L'arbre de décodage de cette méthode est illustré à la figure 10.III.



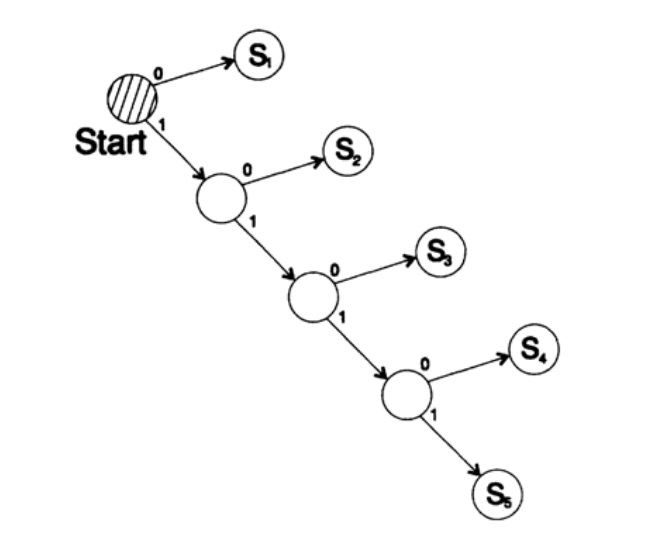Figure 10.III

Deuxième voie

s1 = 00; s2 = 01; s3 = 100; s4 = 110, s5 = 111 ,

L'arbre de décodage de cette prise en charge est illustré à la figure 10.IV.

La façon la plus évidente de mesurer la qualité du code est la longueur moyenne d'un ensemble de messages. Pour cela, il est nécessaire de calculer la longueur de code de chaque caractère multipliée par la probabilité d'occurrence correspondante de pi. Ainsi, la longueur de tout le code est obtenue. La formule pour la longueur moyenne L du code pour un alphabet de q caractères est la suivante



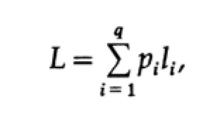
où pi est la probabilité d'occurrence du symbole si, li est la longueur correspondante du symbole codé. Pour un code efficace, la valeur de L doit être aussi petite que possible. Si P1 = 1/2, p2 = 1/4, p3 = 1/8, p4 = 1/16 et p5 = 1/16, alors pour le code # 1, nous obtenons la valeur de longueur de code



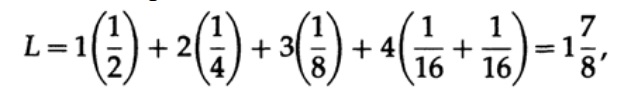
Et pour le code # 2



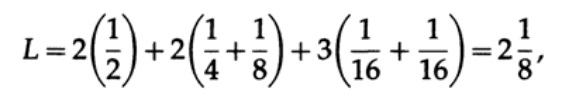
Les valeurs obtenues indiquent la préférence du premier code.
Si tous les mots de l'alphabet ont la même probabilité d'occurrence, alors le deuxième code sera plus préférable. Par exemple, avec pi = 1/5, longueur de code # 1



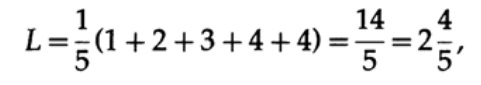
et longueur de code # 2



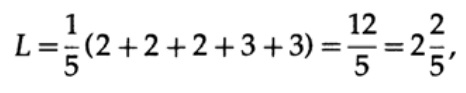
ce résultat montre une préférence pour 2 codes. Ainsi, lors du développement d'un «bon» code, il est nécessaire de considérer la probabilité d'occurrence de caractères.



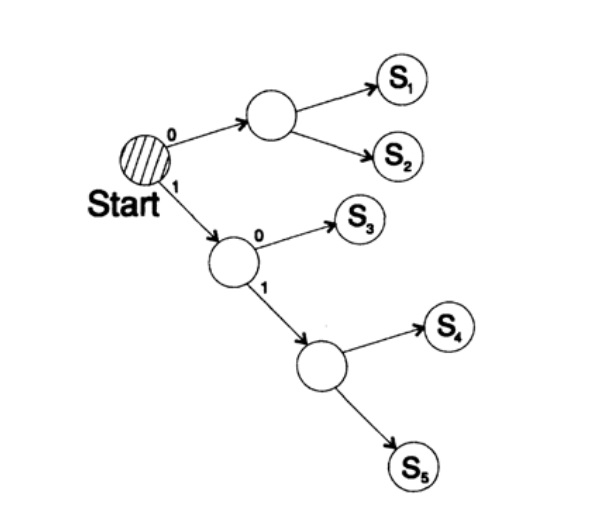Figure 10.IV



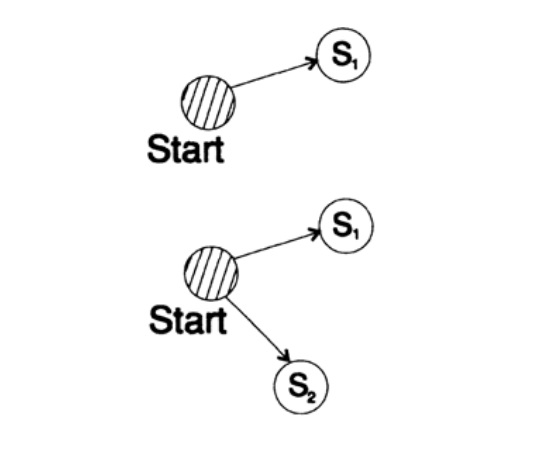Figure 10.V

Considérons l'inégalité Kraft, qui détermine la valeur limite de la longueur du code symbole li. Dans la base 2, l'inégalité est représentée comme



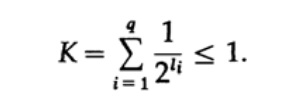
Cette inégalité suggère que l'alphabet ne peut pas avoir trop de caractères courts, sinon la somme sera assez grande.

Pour prouver l'inégalité de Kraft pour tout code décodé unique rapide, nous construisons un arbre de décodage et appliquons la méthode d'induction mathématique. Si un arbre a une ou deux feuilles, comme le montre la figure 10.V, l'inégalité est sans aucun doute vraie. De plus, si l'arbre a plus de deux feuilles, alors nous divisons l'arbre de long m en deux sous-arbres. Selon le principe d'induction, nous supposons que l'inégalité est vraie pour chaque branche de hauteur m -1 ou moins. Selon le principe d'induction, appliquer l'inégalité à chaque branche. Notons les longueurs des codes des branches K 'et K' '. Lors de la combinaison de deux branches d'un arbre, la longueur de chacune augmente de 1, par conséquent, la longueur du code se compose des sommes K '/ 2 et K' '/ 2,



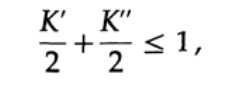
le théorème est prouvé.

Considérez la preuve du théorème de Macmillan. Nous appliquons l'inégalité Kraft aux codes de décodage sans fil. La preuve est basée sur le fait que pour tout nombre K> 1, la nième puissance du nombre est évidemment plus qu'une fonction linéaire de n, où n est un nombre assez important. Nous élevons l'inégalité de Kraft à la nième puissance et présentons l'expression comme une somme



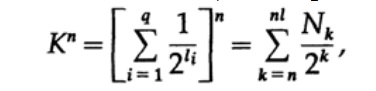
où Nk est le nombre de caractères de longueur k, la sommation commence par la longueur minimale de la nième représentation du caractère et se termine par la longueur maximale nl, où l est la longueur maximale du caractère codé. De l'exigence d'un décodage unique, il s'ensuit que. Le montant est présenté comme



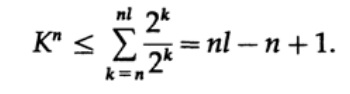
Si K> 1, alors il faut établir n suffisamment grand pour que l'inégalité devienne fausse. Par conséquent, k <= 1; Le théorème de Macmillan est prouvé.

Prenons quelques exemples d'application de l'inégalité Kraft. Un code décodé unique peut-il exister avec les longueurs 1, 3, 3, 3? Oui, depuis



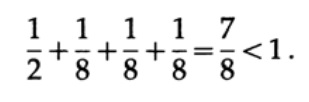
Qu'en est-il des longueurs 1, 2, 2, 3? Calculez selon la formule



L'inégalité violée! Il y a trop de caractères courts dans ce code.

Les codes virgule sont des codes composés de caractères 1, se terminant par un caractère 0, à l'exception du dernier caractère composé de tous les caractères. L'un des cas particuliers est le code.

s1 = 0; s2 = 10; s3 = 110; s4 = 1110; s5 = 11111.

Pour ce code, on obtient l'expression de l'inégalité Kraft



Dans ce cas, nous atteignons l'égalité. Il est facile de voir que pour les codes de point, l'inégalité de Kraft dégénère en égalité.

Lors de la construction d'un code, vous devez faire attention à la quantité de Kraft. Si le montant de Kraft commence à dépasser 1, alors c'est un signal sur la nécessité d'inclure un caractère d'une longueur différente pour réduire la longueur moyenne du code.

Il convient de noter que l'inégalité de Kraft ne signifie pas que ce code est uniquement décodable, mais qu'il existe un code avec des caractères d'une telle longueur qui est décodé de manière unique. Pour construire un code décodé unique, vous pouvez affecter la longueur correspondante en bits li avec un nombre binaire. Par exemple, pour les longueurs 2, 2, 3, 3, 4, 4, 4, 4, on obtient l'inégalité Kraft



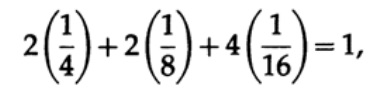
Par conséquent, un tel code de flux décodé unique peut exister.

s1 = 00; s2 = 01; s3 = 100; s4 = 101;

s5 = 1100; s6 = 1101; s7 = 1110; s8 = 1111;

Je veux faire attention à ce qui se passe réellement lorsque nous échangeons des idées. Par exemple, à ce stade, je veux transférer l'idée de ma tête à la vôtre. Je prononce quelques mots à travers lesquels, je crois, vous pouvez comprendre (comprendre) cette idée.

Mais quand un peu plus tard vous voudrez transmettre cette idée à votre ami, vous prononcerez certainement des mots complètement différents. En fait, le sens ou la signification n'est enfermé dans aucun mot spécifique. J'ai utilisé quelques mots, et vous pouvez en utiliser des mots complètement différents pour transmettre la même idée. Ainsi, différents mots peuvent transmettre la même information. Mais, dès que vous dites à votre interlocuteur que vous ne comprenez pas le message, alors en règle générale, l'interlocuteur sélectionnera un ensemble de mots différent, le deuxième ou même le troisième, pour transmettre le sens. Ainsi, les informations ne sont pas enfermées dans un ensemble de mots spécifiques. Dès que vous recevez tel ou tel mot, alors vous faites beaucoup de travail pour traduire les mots en l'idée que l'interlocuteur veut vous transmettre.

Nous apprenons à sélectionner des mots afin de nous adapter à l'interlocuteur. Dans un sens, nous choisissons des mots correspondant à nos pensées et au niveau de bruit dans le canal, bien qu'une telle comparaison ne reflète pas exactement le modèle que j'utilise pour représenter le bruit dans le processus de décodage. Dans les grandes organisations, un problème grave est l’incapacité de l’interlocuteur à entendre ce qu’une autre personne a dit. Aux postes supérieurs, les employés entendent ce qu'ils «veulent entendre». Dans certains cas, vous devez vous en souvenir lorsque vous montez dans l'échelle de carrière. La présentation des informations sous une forme formelle est un reflet partiel des processus de notre vie et a trouvé une large application bien au-delà des limites des règles formelles dans les applications informatiques.

À suivre ...

Qui veut aider à la traduction, la mise en page et la publication du livre - écrivez dans un e-mail personnel ou par courrier électronique magisterludi2016@yandex.ru

Soit dit en passant, nous avons également lancé la traduction d'un autre livre sympa - «The Dream Machine: The History of the Computer Revolution» )