Qu'est-il arrivé au paradoxe de Fermi

Le paradoxe de Fermi est que la probabilité d'une civilisation extraterrestre est généralement estimée assez élevée, et il n'y a rien pour voir des signes de son existence. Récemment, une préimpression par Sanders et co-auteurs de "Dissolving the Fermi paradox" est apparue sur arxiv, qu'ils ont déjà interprété comme annulant ce paradoxe (vrai), bavardage inactif en l'absence de données (plutôt vrai, mais vrai pour le paradoxe de Fermi en général, et pas seulement pour cet article) , et comme preuve de l'inexistence d'étrangers et / ou de faible L (mensonge). Dans cet article, nous allons essayer de comprendre ce que contient réellement la préimpression.

Quel est le problème?

Tout d'abord, l'équation de Drake elle-même. Il est présenté au KDPV; le dernier facteur est une blague, et le reste doit être compris comme suit: dans l'univers observable (ou notre galaxie, ou tout autre volume d'espace) $$ étoiles. Chaque étoile avec probabilité $$ a des planètes. Chacune de ces planètes est susceptible $$ situé dans la zone Goldilocks, a une composition chimique appropriée, etc. Sur chaque planète potentiellement capable de soutenir la vie avec probabilité $$ (par unité de temps) survient une vie qui est susceptible $$ atteint le caractère raisonnable et avec probabilité $$ entre en contact. Et enfin, toute espèce intelligente qui se présente existe $$ ans de la naissance à l'extinction. Si vous multipliez tout cela, vous obtenez le nombre d'espèces intelligentes dans cette zone.

Le temps entre l'origine de l'esprit et l'apparition d'une civilisation notable à des distances interstellaires est négligé. Dans le cas de la Terre, par exemple, des milliards d'années se sont écoulées de l'apparition de la planète à l'apparition de la vie et de l'apparition de la vie à l'apparition de l'espèce Homo sapiens . Le progrès technologique est incomparablement plus rapide - l'émergence d' Homo sapiens du message d'Arecibo sépare moins de dix millions d'années. La colonisation interstellaire n'a pas encore commencé, mais c'est aussi le pire des cas depuis quelques millions d'années. Par rapport aux étapes pré-technologiques - dans la marge d'erreur.

Ce qui, pour le dire avec plus de tact, est assez élevé . De l'ordre de grandeur du nombre d'étoiles et de la probabilité d'avoir des planètes jusqu'à 200 ordres de grandeur (deux cents ordres de grandeur, les estimations diffèrent par $$ fois) pour la probabilité d'abiogenèse. Ce travail ingrat consiste à évaluer les probabilités à partir d'une seule observation. Cependant, les scientifiques ont publié diverses estimations $$ et est venu le plus souvent à la conclusion que $$ , et même $$ . En fait, quel est le paradoxe de Fermi: selon nos meilleures estimations, il doit y avoir d'autres races intelligentes dans la galaxie, et il n'y avait aucune preuve fiable de leur existence.

Le problème n'est évidemment pas dans la galaxie: si les estimations diffèrent de la réalité observée, alors tant pis pour les estimations. Soit l'un des paramètres est grandement surestimé ( et que Dieu nous bénisse, s'il s'agit de L ), soit nous pensons d'une manière ou d'une autre incorrecte. Sandberg et al préconisent simplement la dernière version.

Et comment compter correctement?

Il semblerait multiplier une poignée de nombres réels - pas le binôme de Newton. Le hic, c'est que dans une telle situation, la multiplication des nombres repose sur l'hypothèse qu'ils sont de toute façon précisément connus de nous. Comme nous l'avons vu plus haut, cette hypothèse est très éloignée de la réalité.

Prenons un exemple simplifié: laissez l'équation de Drake avoir neuf paramètres et tous les neuf sont uniformément répartis dans la plage $$ . La meilleure estimation ponctuelle pour chacun de ces paramètres est de 0,1 et leur produit donne une probabilité d'une civilisation par milliard d'étoiles. Dans la galaxie depuis $$ quelque 100 civilisations devraient apparaître dans les étoiles, et la probabilité que cela ne se produise jamais - $$ . De telles probabilités sont généralement illustrées par des phrases telles que «si chaque atome dans <une chose très grande comme le système solaire> pendant <une très longue période comme son âge>». Ce qui dans ce cas semble tout à fait approprié, mais en fait il est impossible de ne pas rejeter une hypothèse aussi nulle. Le paradoxe de Fermi prend toute sa hauteur.

Si nous n'utilisons pas d'estimations ponctuelles et que pour chaque paramètre, nous prenons une valeur aléatoire dans la plage correspondante, la galaxie est vide dans 21,45% des simulations. Le fait que quelque chose se soit produit avec une probabilité d'un peu plus d'un cinquième n'est nullement un paradoxe. Il est légèrement moins probable qu'une paire de rois batte toutes les autres mains sur une table de Hold'em de 9 joueurs , et avec les rois de poche, je fais personnellement tapis à la première occasion.

La même logique peut être appliquée aux estimations réelles des paramètres de l'équation de Drake. Si vous les collectez dans la littérature et exécutez la simulation, vous obtenez l'image suivante:



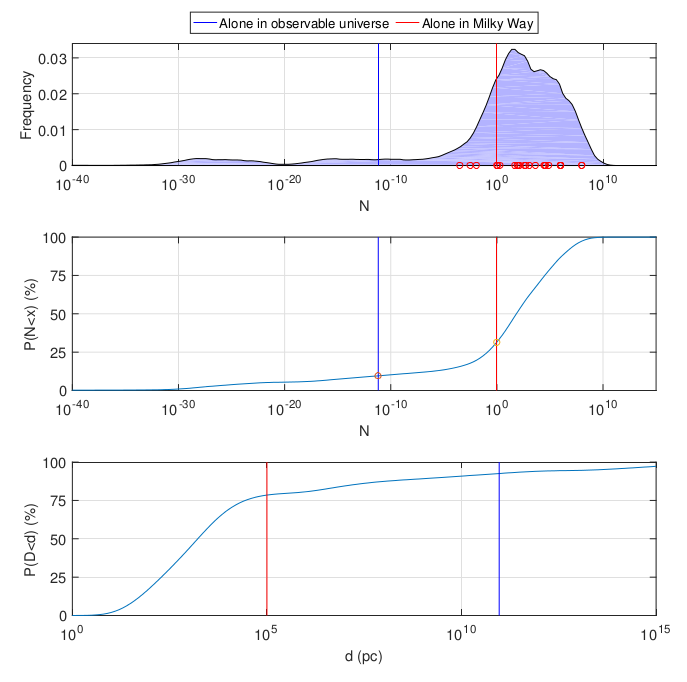
De haut en bas: la fonction de densité de probabilité pour le nombre de civilisations dans notre galaxie, la densité de distribution cumulée pour elle, la densité de distribution cumulée de la distance à la civilisation observable la plus proche en parsecs. Tout est à l'échelle logarithmique. Les lignes rouges et bleues indiquent la probabilité que nous soyons la seule civilisation de notre galaxie et de l'univers observable. Cercles dans le graphique supérieur - notes littéraires normalisées $$ .

Dans l'ensemble, le résultat est plutôt optimiste: la plus grande densité de probabilité tombe sur la multiplicité des civilisations (moyenne 53 millions, médiane 100). Mais aux fins du paradoxe de Fermi, les chiffres sont approximativement les mêmes que dans un exemple simplifié: avec une probabilité de vingt pour cent ou quelque chose, la Voie lactée ne contient qu'une seule civilisation (la nôtre). Soit dit en passant, une conséquence plutôt contre-intuitive: la probabilité que la Voie lactée, sans compter la Terre , contienne exactement une civilisation (sauf la nôtre) est pratiquement la même.

Au lieu de prendre des estimations de paramètres directement à partir de la littérature, les distributions peuvent être construites et calculées analytiquement. Une gamme d'estimations est prise jusqu'à un ordre de grandeur et chaque paramètre est considéré comme log-normal ou log-uniformément distribué dans l'intervalle correspondant. Le résultat se déplace quelque peu vers la gauche, mais la signification est la même:



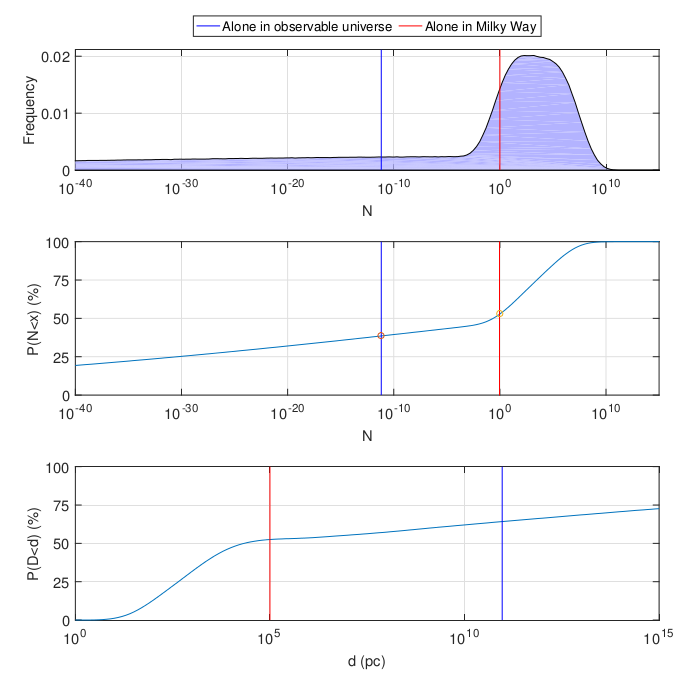
Qu'est-ce que tout cela signifie? La bonne réponse à la question "est-ce qu'il y a de la vie dans l'univers ou n'est-ce pas là" toujours "je ne sais pas". Comment les statistiques bayésiennes agréablement élégantes coûtent peu en l'absence de données expérimentales. La réponse à la question «Dans quelle mesure devrions-nous être surpris de ce qui a été observé a changé $$ " Auparavant, il était «très fort, donc soit la vie est une chose très rare, soit nous mourrons tous dans une guerre nucléaire ou quelque chose comme ça », et maintenant c'est devenu «Eh bien, en principe, ce n'est pas très probable, mais rien d'extraordinaire.» La probabilité d'une guerre nucléaire et / ou d'une rencontre avec un dinosaure sur des extraterrestres Nevsky n'est tombée que dans le sens bayésien: nous sommes légèrement moins sûrs que cela se produira. Que ces événements se produisent réellement ou non dépend des facteurs du monde réel (à peu près, Poutine, Trump et Zorblaks, le Galactic Eater), et non des mathématiques utilisées pour en discuter.