Encodeurs automatiques et forte intelligence artificielle

La théorie des auto-encodeurs et des modèles générateurs a récemment été sérieusement développée, mais pas mal de travaux sont consacrés à leur utilisation dans les problèmes de reconnaissance. Dans le même temps, la propriété des auto-encodeurs d'obtenir un modèle de données paramétriques caché et les conséquences mathématiques de celui-ci permettent de les associer aux méthodes décisionnelles bayésiennes.

L'article propose un appareil mathématique original «un ensemble d'auto-encodeurs avec un espace latent commun», qui vous permet d'extraire des concepts abstraits des données d'entrée et démontre la capacité à «l'apprentissage ponctuel». De plus, il peut être utilisé pour surmonter de nombreux problèmes fondamentaux des algorithmes modernes d'apprentissage automatique basés sur des réseaux multicouches et l'approche «Deep learning».

Contexte

Les réseaux de neurones artificiels, formés à l'aide du mécanisme de rétropropagation des erreurs, ont presque remplacé d'autres approches dans de nombreux problèmes de reconnaissance et d'estimation des paramètres. Mais ils présentent un certain nombre d'inconvénients qui, semble-t-il, ne peuvent être éliminés sans une révision sérieuse de l'approche:

1. instabilité extrême pour saisir des données non trouvées dans l'échantillon de formation (y compris dans le cas d'attaques contradictoires)
   
   
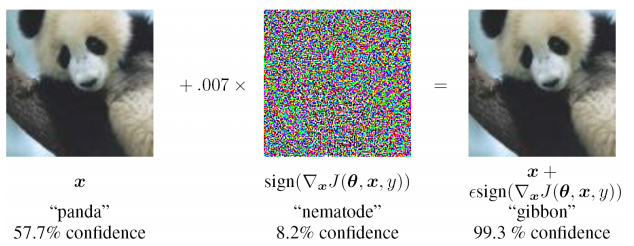
2. il est difficile d'évaluer la source du problème et de se recycler localement à l'un des niveaux (il suffit de compléter l'échantillon de formation et de se recycler), c'est-à-dire problème de boîte noire
3. la possibilité d'interprétations différentes des mêmes informations d'entrée n'est pas fournie, la nature statistique des données observées est ignorée
   
   

Étant engagé dans la résolution de problèmes appliqués et en s'appuyant sur un certain nombre d'ouvrages existants, je propose une approche qui est sensiblement différente des travaux existants, élimine un certain nombre de leurs lacunes et est applicable pour résoudre des problèmes appliqués dans divers domaines de l'apprentissage automatique.

Encodeur automatique pour estimer la densité de distribution

Dans la théorie de la prise de décision, une place très importante est occupée par la densité de distribution (ou fonction de distribution) des variables aléatoires. Il est nécessaire d'avoir des estimations des fonctions de distribution pour calculer le risque postérieur.

Il s'avère que les encodeurs automatiques sont très naturels pour évaluer les fonctions de distribution. Cela peut s'expliquer comme suit: l'ensemble de données d'apprentissage est déterminé par la densité de leur distribution. Plus la densité d'exemples d'apprentissage est élevée autour d'un point local dans l'espace d'entrée, mieux l'auto-encodeur reconstruit le vecteur d'entrée à cet emplacement dans l'espace. De plus, à l'intérieur de l'autoencodeur, il y a un vecteur de représentation latente des données d'entrée (généralement de faible dimension), et si les données sont projetées dans l'espace latent dans une zone qui n'a pas été précédemment utilisée dans la formation, alors il n'y avait rien de similaire dans l'échantillon d'apprentissage.

Il existe un certain nombre d'œuvres fermées et quelque peu isolées:

1. Alain, G. et Bengio, Y. Ce que les autoencodeurs régularisés apprennent de la distribution de génération de données. 2013.
2. Kamyshanska, H. 2013. Sur la notation de l'encodeur automatique
3. Daniel Jiwoong Im, Mohamed Ishmael Belghazi, Roland Memisevic. 2016. Conservativité des auto-encodeurs non liés

Le premier justifie que le résultat de la reconstruction de débruitage des auto-encodeurs est lié à la fonction de densité de probabilité des données d'entrée, mais un certain nombre de restrictions sont imposées aux auto-encodeurs. La seconde contient des exigences suffisantes pour l'encodeur automatique - les poids de l'encodeur et du décodeur doivent être «connectés», c'est-à-dire la matrice de pondération de la couche codeur est la matrice transposée du décodeur. Dans le dernier travail, les conditions nécessaires et suffisantes pour le fait que le codeur automatique est associé à une densité de probabilité sont étudiées plus en détail.

Ces travaux étayent strictement la base théorique de la relation des autoencodeurs avec la densité de distribution des données de formation. Dans les problèmes appliqués, une analyse aussi sérieuse n'est souvent pas nécessaire, par conséquent, une approche légèrement différente sera donnée ci-dessous qui nous permettra d'estimer la fonction de densité de probabilité des données d'entrée grâce à un autoencodeur préalablement formé.

Exemple MNIST

Dans des travaux encore antérieurs, l'idée empirique a été proposée que pour le problème de classification, il est possible de former des auto-encodeurs par le nombre de classes (en enseignant chacune d'elles uniquement sur le sous-échantillon correspondant). Et choisissez comme réponse la classe et l'encodeur automatique qui donnent le minimum d'écart entre l'image d'entrée et l'image reconstruite. Il n'a pas été difficile de vérifier sur MNIST: pour former 10 auto-encodeurs (pour chaque chiffre), calculer la précision, puis comparer avec un modèle multicouche similaire du classificateur.

Scripts de formation et de test sur git (train_ae.py, calc_codes.py, calc_acc.py)

Architecture et nombre de poids:



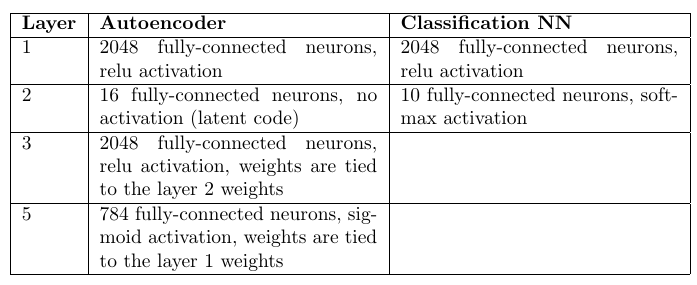
Encodeurs automatiques: 98,6%
Classificateur de perceptron multicouche: 98,4%

Un lecteur attentif remarquera qu'il y avait 10 fois plus de poids dans les encodeurs automatiques (par leur nombre). Cependant, une augmentation de 10 fois du nombre de poids dans la couche cachée dans un perceptron multicouche ne fait qu'aggraver les statistiques.

Bien sûr, les réseaux de convolution offrent une précision beaucoup plus élevée, mais la tâche consistait uniquement à comparer les approches, toutes choses étant égales par ailleurs.

En conséquence, on peut noter que l'approche avec les auto-encodeurs est assez compétitive avec les réseaux entièrement connectés. Et même s'il faut beaucoup plus de temps pour optimiser les poids, il présente un avantage important: la capacité de détecter des anomalies dans les données d'entrée. Si aucun des auto-encodeurs n'a pu reconstruire avec précision l'image d'entrée, alors nous pouvons affirmer qu'une image anormale qui ne s'est pas produite dans l'échantillon d'apprentissage a été entrée. À strictement parler, vous pouvez reconstruire une image non pas à partir de l'échantillon d'entrée, mais ce qu'il faut faire dans cette situation sera montré plus tard.

Considérons un seul encodeur automatique

Il est possible, d'une manière légèrement différente de celle des articles ci-dessus, d'effectuer une analyse qualitative de la relation entre la densité de probabilité des données d'entrée p (x) et la réponse de l'autoencodeur.

Encodeur automatique - utilisation séquentielle de la fonction d'encodeur $$$z = g (x)$ et décodeur $$$x ^ * = f (z)$ où $$$x$ Est le vecteur d'entrée, et $$$z$ - performances latentes. Dans un sous-ensemble d'entrées (généralement proche de la formation) $$$x ^ * = x + n = f (g (x))$ où $$$n$ - divergence. Nous acceptons la différence du bruit de Gausovsky (ses paramètres peuvent être estimés après la formation de l'autoencodeur). En conséquence, un certain nombre d'hypothèses assez solides sont émises:

1) divergence - bruit gaussien
2) l'encodeur automatique est déjà «formé» et fonctionne

Mais, surtout, presque aucune restriction ne sera imposée à l'auto-encodeur lui-même.

En outre, une estimation qualitative de la densité de probabilité p (x) peut être obtenue, sur la base de laquelle plusieurs conclusions très importantes à l'avenir peuvent être tirées.

Score P (x) pour un seul encodeur automatique

Densité de distribution pour $$$x \ dans X$ et $$$z \ in Z$ liés comme suit:

$$

$$p (x) = \ int_ {z} p (x | z) p (z) dz \; \; \; (1)$$

Nous devons obtenir la connexion p (x) et p (z). Pour certains encodeurs automatiques, p (z) est défini au stade de leur apprentissage; pour d'autres, p (z) est encore plus facile à obtenir en raison de la plus petite dimension Z.

La distribution de densité du n résiduel est connue, ce qui signifie:

$$

$$p (n) = const \ times exp (- \ frac {(xf (z)) ^ T (xf (z))} {2 \ sigma ^ 2}) = p (x | z) \; \; ( 2)$$

$$$(x-f (z)) ^ T (x-f (z))$ Est la distance entre x et sa projection x *. À un certain point z *, cette distance atteindra son minimum. À ce stade, les dérivées partielles de l'argument de l'exposant dans la formule (2) par rapport à $$$z_i$ (Axe Z) sera nul:

$$

$$0 = \ frac {\ partial f (z ^ *)} {\ partial z_i} ^ T (xf (z ^ *)) + (xf (z ^ *)) ^ T \ frac {\ partial f (z ^ * )} {\ partial z_i}$$

Ici $$$\ frac {\ partial f (z ^ *)} {\ partial z_i} ^ T (x-f (z ^ *))$ scalaire alors:

$$

$$0 = \ frac {\ partial f (z ^ *)} {\ partial z_i} ^ T (x-f (z ^ *)) \; \; \; (3)$$

Le choix du point z *, où la distance $$$(x-f (z)) ^ T (x-f (z))$ minime en raison du processus d'optimisation de l'encodeur automatique. Pendant l'entraînement, c'est le résidu quadratique qui est minimisé (en règle générale): $$$\ min \ limits _ {\ theta, \ forall x \ in X train} L2_ {norm} ({x-f_ \ theta (g_ \ theta (x))})$ où $$$\ theta$ - le poids de l'encodeur. C'est-à-dire après l'entraînement, g (x) tend vers z *.

Nous pouvons également étendre $$$f (z)$ dans une série de Taylor (jusqu'au premier terme) autour de z *:

$$

$$f (z) = f (z ^ *) + \ nabla f (z ^ *) (z-z ^ *) + o ((z-z ^ *))$$

Donc, maintenant l'équation (2) devient:

$$

$$p (x | z) \ approx const \ times exp (- \ frac {((xf (z ^ *)) - \ nabla f (z ^ *) (zz ^ *)) ^ T ((xf (z ^ *)) - \ nabla f (z ^ *) (zz ^ *))} {2 \ sigma ^ 2}) =$$

$$

$$= const \ times exp (- \ frac {(xf (z ^ *)) ^ T (xf (z ^ *))} {2 \ sigma ^ 2}) exp (- \ frac {(\ nabla f (z ^ *) (zz ^ *)) ^ T (\ nabla f (z ^ *) (zz ^ *))} {2 \ sigma ^ 2}) \ times$$

$$

$$\ times exp (- \ frac {(\ nabla f (z ^ *)) ^ T (xf (z ^ *)) + (xf (z ^ *)) ^ T \ nabla f (z ^ *)) (zz ^ *)} {2 \ sigma ^ 2})$$

Notez que le dernier facteur est 1 en raison de l'expression (3). Le premier facteur peut être supprimé par le signe de l'intégrale (il ne contient pas z) dans (1). Et supposons également que p (z) est une fonction suffisamment lisse et ne change pas beaucoup au voisinage de z *, c'est-à-dire remplacer p (z) -> p (z *).

Après toutes les hypothèses, l'intégrale (1) a l'estimation:

$$

$$p (x) = const \ times p (z ^ *) exp (- \ frac {(xf (z ^ *)) ^ T (xf (z ^ *))} {2 \ sigma ^ 2}) \ int_ {z} exp (- (zz ^ *) ^ TW (x) ^ TW (x) (zz ^ *)) dz, \; \; \; z ^ * = g (x)$$

où $$$W (x) = \ frac {\ nabla f (z ^ *)} {\ sigma}, z ^ * = g (x)$
La dernière intégrale est l'intégrale d'Euler-Poisson à n dimensions:

$$

$$\ int_ {z} exp (- \ frac {(zz ^ *) ^ TW (x) ^ TW (x) (zz ^ *)} {2}) dz = \ sqrt {\ frac {1} {det ( W (x) ^ TW (x) / 2 \ pi)}}$$

En conséquence, nous avons obtenu l'estimation finale p (x):

$$

$$p (x) = const \ times exp (- \ frac {(xf (z ^ * *)) ^ T (xf (z ^ *))} {2 \ sigma ^ 2}) p (z ^ *) \ sqrt {\ frac {1} {det (W (x) ^ TW (x) / 2 \ pi)}}, z ^ * = g (x) \; \; \; (4)$$

Tous ces calculs étaient nécessaires pour montrer que p (x) dépend de trois facteurs:

• La distance entre le vecteur d'entrée et sa reconstruction, pire il est restauré, plus petit p (x)
• Densités de probabilité p (z *) à z * = g (x)
• Normalisation de la fonction p (z) au point z *, qui est calculée pour l'autoencodeur à partir de dérivées partielles de la fonction f

Et à partir de la constante de normalisation, qui sera ensuite responsable de la probabilité a priori de choisir un encodeur automatique pour décrire les données d'entrée.

Malgré toutes les hypothèses, le résultat était très significatif et utile du point de vue des calculs.

Classification des paramètres ou procédure de notation

Vous pouvez maintenant décrire plus précisément la procédure de classification à l'aide d'un ensemble d'auto-encodeurs:

1. Formation de codeurs automatiques indépendants pour chaque classe sur la sortie correspondante
2. Calcul de la matrice W pour chaque autoencodeur
3. Score P (z) pour chaque encodeur automatique

Et pour chaque vecteur d'entrée, vous pouvez évaluer maintenant $$$p (x | classe)$ par le nombre de classes. Et ce sera la fonction de vraisemblance qui est nécessaire pour la prise de décision dans le cadre de la règle bayésienne pour la prise de décision.

De la même manière, des paramètres inconnus peuvent également être estimés en divisant l'espace des paramètres en valeurs discrètes, en entraînant votre propre encodeur automatique pour chaque valeur. Et puis, en fonction du meilleur score bayésien, choisissez la valeur qui donne la fonction de vraisemblance maximale.

Ici, il convient de noter que, formellement, le problème de l'estimation de p (z) n'est pas plus simple que l'estimation de p (x). Mais en pratique, ce n'est pas le cas. L'espace Z a généralement une dimension beaucoup plus petite, ou la distribution est généralement définie lors de l'optimisation des poids de l'auto-encodeur.

L'idée de combiner l'espace latent des auto-encodeurs

Il y a une curieuse interprétation proposée par Alexei Redozubov et décrite dans les articles suivants:

1. Une architecture de réseau neuronal artificiel basée sur des transformations de contexte dans des minicolonnes corticales. Vasily Morzhakov, Alexey Redozubov
2. Mémoire holographique: un nouveau modèle de traitement de l'information par les microcircuits neuronaux. Alexey Redozubov, Springer
3. Pas du tout des réseaux de neurones. Morzhakov V.

Les informations peuvent avoir une interprétation complètement différente dans différents contextes. Le modèle d'un «ensemble d'encodeurs automatiques» fait écho à cette idée proposée. Tout encodeur automatique est un modèle latent de données d'entrée dans le même contexte (une classe ou d'autres paramètres fixes), c'est-à-dire le vecteur latent est une interprétation et chaque auto-encodeur est un contexte. Lors de la réception des informations d'entrée, elles sont prises en compte dans chaque contexte (par chaque auto-encodeur), et le contexte est sélectionné qui prend très probablement en compte les modèles existants dans chaque auto-encodeur.

La prochaine étape raisonnable consiste à permettre l'intersection des interprétations dans différents contextes. C'est-à-dire pendant la formation, on sait souvent que l'interprétation reste la même, mais la forme de présentation (contexte) change. Par exemple, l'orientation d'un objet change, mais l'objet reste le même. Le vecteur de la description de l'objet doit être conservé et l'orientation contextuelle change.

Ensuite, si nous examinons la formule (4), le facteur p (z) s'avère être estimé pour l'ensemble des auto-encodeurs, et non pour chacun séparément. L'interprétation (vecteur latent) aura une distribution commune. Pour un petit nombre d'auto-encodeurs, cela peut ne pas avoir un rôle important, mais dans une vraie tâche, ce nombre peut être énorme. Par exemple, si vous définissez un contexte pour chaque orientation possible d'un objet 3D, il peut y en avoir des centaines de milliers. Maintenant, chaque exemple présenté pour la formation dans n'importe quel contexte formera une distribution p (z).

Interchangeabilité d'interprétation et de contexte

Dans le problème appliqué, la question se pose immédiatement: que faut-il attribuer par interprétation, et quoi par contexte? Le contexte et l'interprétation peuvent être facilement échangés, et personne n'exclut la possibilité du fonctionnement parallèle simultané d'une paire d '«ensembles d'autoencodeurs».

Pour plus de clarté, vous pouvez proposer cet exemple:

L'image d'entrée contient les visages des personnes.

1. contexte - orientation du visage. Ensuite, pour la reconstruction de l'image d'entrée, nous n'avons pas assez d '«interprétation» - un code qui identifie une personne, qui contiendra une description du visage, de la coiffure, de son éclairage. Pendant la formation, nous devrons présenter le même visage de différents côtés, «geler» le code latent, tout en changeant l'orientation.
2. contexte - type de visage, d'éclairage, de coiffure. Ensuite, pour la reconstruction de l'image d'entrée, il nous manque l'orientation du visage. Pendant l'entraînement, il sera nécessaire de montrer différents visages dans différentes conditions d'éclairage, mais avec la même orientation.

La décision bayésienne optimale dans le premier cas sera prise en ce qui concerne l'orientation du visage, et dans le second - son type. Vraisemblablement, la première option donnera une meilleure précision d'orientation, et la seconde évaluera plus précisément de qui il s'agissait.

Apprentissage d'un ensemble d'auto-encodeurs avec espace latent partagé

En formation, nous devons savoir à quoi ressemble une entité en termes de sens dans différents contextes. Par exemple, si nous parlons de l'image des nombres et de l'orientation contextuelle, alors schématiquement, une telle formation croisée ressemble à ceci:



L'encodeur d'un auto-encodeur est utilisé, puis le code latent est décodé par le décodeur d'un autre auto-encodeur. La fonction de perte d'apprentissage reste standard. Il est intéressant de noter que si l'auto-encodeur est sélectionné symétriquement (c'est-à-dire que les poids de l'encodeur et du décodeur sont connectés), alors à chaque itération tous les poids des deux auto-encodeurs sont optimisés.

Le plus pratique pour une formation aussi délicate était PyTorch, qui vous permet de créer des schémas assez complexes pour la propagation arrière des erreurs, y compris dynamiques.

Les étapes d'apprentissage standard de chaque encodeur automatique alternent avec l'itération de la formation croisée. En conséquence, tous les auto-encodeurs ont un espace latent ou «interprétation» commun dans différents contextes.

Il est très important qu'à la suite d'une telle analyse, nous puissions diviser les informations d'entrée en «contexte» et «interprétation».

Exemple de formation

Prenons un exemple assez simple basé sur MNIST, qui aidera à démontrer le principe de la formation des autoencodeurs avec un espace latent commun. En conséquence, cet exemple démontrera la formation du concept abstrait de «cube» en utilisant le mécanisme décrit dans l'article.

Les nombres de MNIST sont tracés sur le bord du cube et il tourne autour de l'un de ses axes:



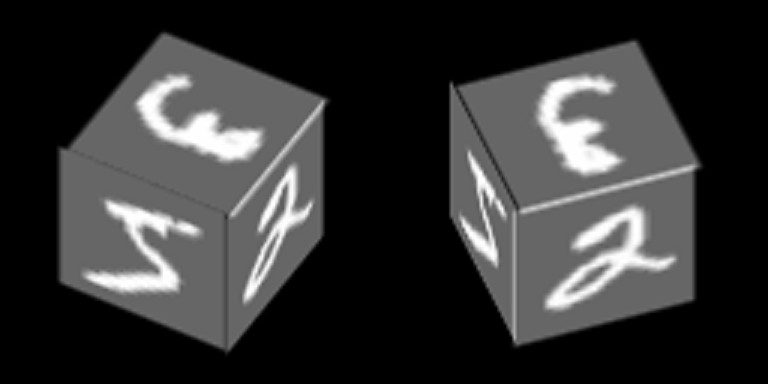
Nous formerons des autoencodeurs pour restaurer les visages, l'orientation contextuelle des visages.

Voici un exemple du nombre «zéro» dans 100 contextes, dont les 34 premiers correspondent à différents angles de rotation de la face latérale et les 76 restants - différents angles de rotation de la face supérieure.



Nous supposons que pour chacune de ces 100 images, les «interprétations» devraient être les mêmes, et ce sont leurs combinaisons aléatoires qui sont utilisées pour la formation croisée.

Après une formation avec la méthode décrite ci-dessus, il a été possible de réaliser que le code latent de l'un des encodeurs automatiques puisse être décodé par d'autres encodeurs automatiques, obtenant une conversion contextuelle vraiment significative.

Par exemple, cette image montre comment le résultat de l'encodage de l'encodeur automatique au numéro 10 est décodé par d'autres encodeurs automatiques pour l'un des chiffres:



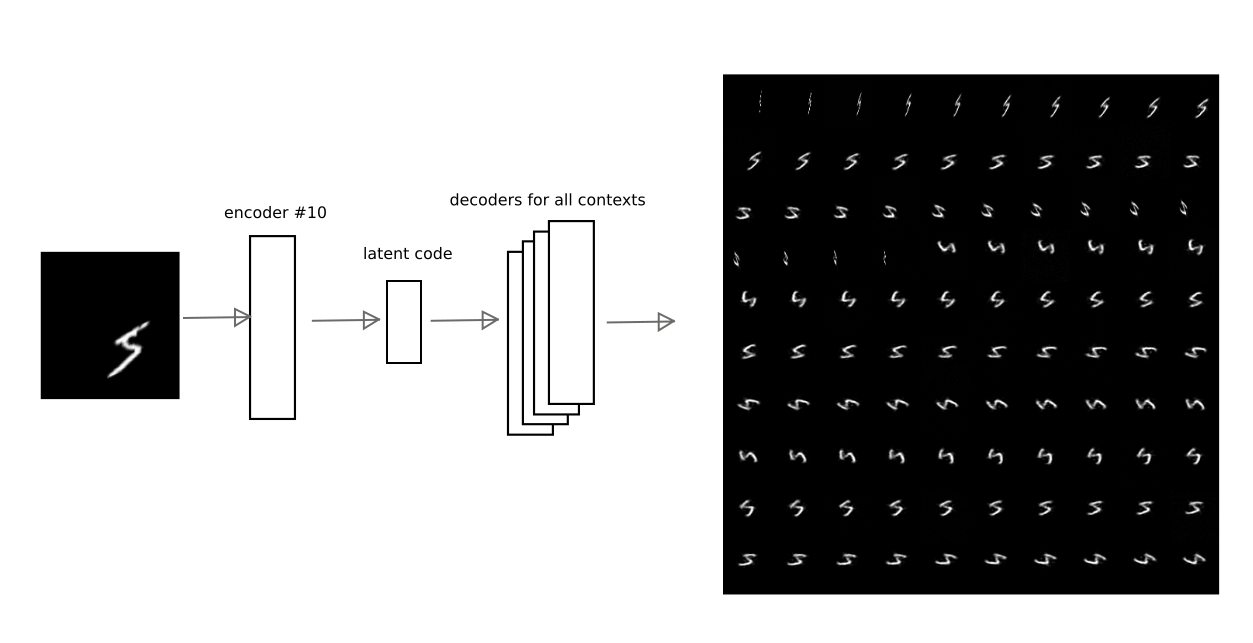
Ainsi, avoir le code de "l'interprétation", c'est-à-dire vecteur latent de l'encodeur automatique, vous pouvez restaurer l'image d'origine dans n'importe quel contexte formé (c'est-à-dire le décodeur de tout encodeur automatique).

Masquage vectoriel d'entrée

Dans la formule (4), la dispersion du résidu $$$\ sigma$ , qui est choisi par une constante pour n'importe laquelle des composantes du vecteur d'entrée. Cependant, si certains composants n'ont pas de relation statistique avec le modèle latent, la variance sera probablement significativement plus élevée pour ces composants. La dispersion est partout dans le dénominateur, ce qui signifie que plus l'écart est grand, moins la contribution de l'erreur de composante est importante. Vous pouvez associer cela à un masquage d'une partie du vecteur d'entrée.

Pour cet exemple avec des visages en rotation, le masque est évident - la projection du visage dans un contexte spécifique.



Dans l'approche simplifiée de cet exemple, qui utilise uniquement le résiduel entre l'image d'entrée et la reconstruction, il vous suffit de multiplier le résiduel par le masque pour chacun des contextes.

Dans le cas général, il est nécessaire d'évaluer plus strictement les paramètres de distribution, donc sans entrer manuellement le masque.

Séparation de l'interprétation du contexte

En séparant l'interprétation du contexte, vous pouvez obtenir des concepts abstraits. Dans l'exemple entraîné, il est intéressant de démontrer 2 effets:

1) apprentissage ponctuel, c'est-à-dire formation avec un nombre d'exemples extrêmement restreint (dans la limite d'un).

Si nous analysons seulement l'interprétation, en ignorant le contexte, alors il devient possible de reconnaître une nouvelle image dans différentes orientations de visage, lorsqu'une nouvelle image a été montrée dans une seule des orientations.

Il est important de noter qu'une nouvelle image doit être présentée. Par souci d'exactitude, nous nous sommes également fixé pour objectif de ne pas nous souvenir d'une seule image, mais d'apprendre à partager 2 nouvelles images qui ne se trouvaient pas auparavant dans la base de formation du MNIST. Par exemple, tels que:



: (, 10), , , , , ( ).

, . , MNIST, , , , .

V №10 :



, , .

« 1» .

2) et avec le cube, il est intéressant de montrer ce qui se passera si vous ignorez le contenu du vecteur latent, et seul le degré de plausibilité de chaque encodeur automatique est transmis.

Voyons à quoi ressemble la probabilité pour chacun des contextes pour deux cubes avec des textures complètement différentes (numéros 5 et 9) pour 100 contextes qui peuvent être affichés sous forme de carte:



on peut voir que les cartes sont assez similaires, malgré la texture différente sur les côtés du cube.

C'est-à-dire , (), , 3- . , .

, . , , . , .

« №1»

L'ensemble d'auto-encodeurs formés par le MNIST s'applique à deux nouvelles images présentées dans le contexte # 10. Il s'avère 2 points dans l'espace latent correspondant aux signes de V et +. Nous définissons un plan équidistant des deux points, que nous utiliserons pour prendre une décision. Si le point est d'un côté de l'avion - le signe V, de l'autre - le signe plus.

Maintenant, nous obtenons les codes des images converties et pour chacune d'entre elles, nous calculons la distance au plan, en préservant le signe.

En conséquence, il est possible de distinguer quel type de signe a été présenté pour les 100 contextes.

Distribution des distances sur le graphique:



Visualisation du résultat en utilisant des symboles individuels comme exemple:



C'est-à-dire V , V . 100 100 , , .

«one-shot learning», . , , «transfer learning», , , .

git (train_ae_shared.py, test_AB.py)

« №2»

. ( « »). , .

:

1. : 0 90 . 5.
2. , ( ), , ,
3. : , «», , , , , .

5421 5 , :


0 90

, , . 0 1 ( ) , :



1, 100 , «» . «» 3 , , , :



Ou le code du signe V, qui n'a pas été rencontré du tout dans l'ensemble de formation:



la qualité est pire, mais le signe est reconnaissable.

Ainsi, au deuxième niveau de traitement d'image, nous avons obtenu un encodeur automatique qui modélise la variété du concept abstrait de «cube». En pratique, dans les problèmes de reconnaissance, le principe de rétroprojection montré dans l'expérience est extrêmement important, car permet d'éliminer les ambiguïtés d'interprétation dues à la formation de concepts abstraits d'un niveau supérieur.

Lien vers git (second_level.py, second_level_test.py)

Autres exemples où la séparation de contexte fonctionne

. , , « ». , , , (, ).

: 3D ; .

, : — ( ) ( ); ( , ,«- -»).

, . , , , , , :

• , , .
• ,
• , ,
• «»

, , /.

, , . , . ( ), , . (, , .), .

De plus, bien que le Deep Learning soit utilisé dans la formation des auto-encodeurs, les processus se produisant dans les auto-encodeurs sont facilement analysés à chaque niveau de traitement de l'information, car il est possible de déterminer dans quel modèle (ou dans quel contexte) la meilleure interprétation a été trouvée. Et la signification des rétroactions entre les niveaux qui doivent être introduits dans les systèmes complexes est d'augmenter ou de diminuer la probabilité de choisir un contexte particulier.

Résultat

, , , . . , — , , .. , — .

, MNIST.

: ( «one-shot learning») .

L'effet de la séparation du contexte de l'interprétation est montré: la possibilité de former des concepts abstraits du niveau suivant en utilisant le «cube» d'abstraction géométrique comme exemple.

Les références

1) Alain, G. and Bengio, Y. What regularized autoencoders learn from the data generating distribution. 2013.
2) Kamyshanska, H. 2013. On autoencoder scoring
3) Daniel Jiwoong Im, Mohamed Ishmael Belghazi, Roland Memisevic. 2016. Conservativeness of Untied Auto-Encoders
4) An Artificial Neural Network Architecture Based on Context Transformations in Cortical Minicolumns. Vasily Morzhakov, Alexey Redozubov
5) Holographic Memory: A novel model of information processing by Neural Microcircuits. Alexey Redozubov, Springer
6) . .
7) en.wikipedia.org/wiki/Gaussian_integral
8) Adversarial Examples: Attacks and Defenses for Deep Learning
9) One-Shot Imitation Learning

PS: — , , . !