
Les propriétés des nombres premiers vous permettent rarement de travailler avec eux différemment que sous la forme d'un tableau pré-calculé - et de préférence aussi volumineux que possible. Le format de stockage naturel sous la forme d'entiers de l'une ou l'autre capacité numérique souffre en même temps de certains inconvénients qui deviennent importants avec la croissance du volume de données.
Ainsi, le format des entiers non signés 16 bits avec la taille d'une telle table est d'environ 13 kilo-octets, il ne contient que 6542 nombres premiers: suivi du nombre 65531 sont les valeurs de la profondeur de bits la plus élevée. Une telle table ne convient que comme jouet.
Le format entier 32 bits le plus populaire en programmation semble beaucoup plus solide - il vous permet d'en stocker environ 203 millions de simples. Mais une telle table occupe déjà environ 775 mégaoctets.
Le format 64 bits a encore plus de perspectives. Cependant, avec une puissance théorique de l'ordre de 1e + 19 valeurs, la table aurait une taille de 64 exaoctets.
On ne croit pas vraiment que notre humanité progressiste calculera jamais dans un avenir prévisible un tableau des nombres premiers d'un tel volume. Et le point ici n'est pas tant dans les volumes que dans le temps de comptage des algorithmes disponibles. Disons que si le tableau de tous les simples 32 bits peut encore être calculé indépendamment en quelques heures (Fig.1), alors pour le tableau au moins un ordre de grandeur plus grand, cela prendra plusieurs jours. Mais de tels volumes aujourd'hui - ce n'est que le niveau initial.
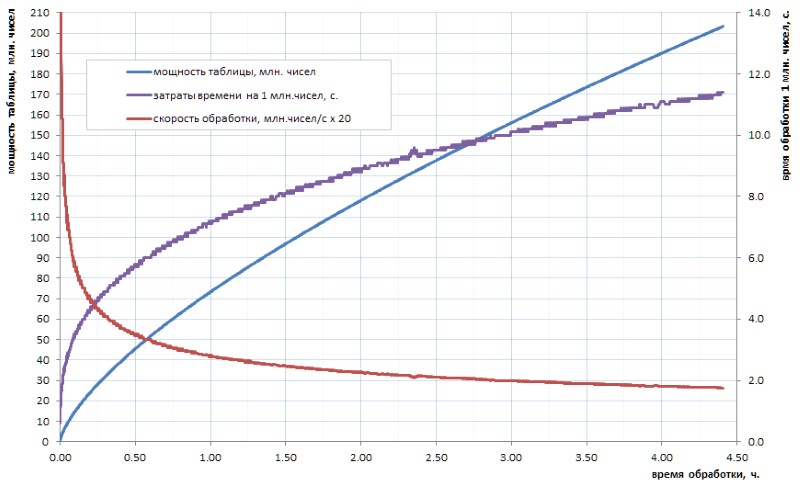
Comme le montre le diagramme, le temps de calcul spécifique après la secousse de début passe en douceur à une croissance asymptotique. Il est plutôt lent. mais c'est la croissance, ce qui signifie que l'extraction de chaque prochaine donnée au fil du temps sera de plus en plus difficile. Si vous voulez faire une percée importante, vous devrez paralléliser le travail à travers les cœurs (et il se parallélise bien) et l'accrocher sur des superordinateurs. Avec la perspective d'obtenir les 10 premiers milliards simples en une semaine, et 100 milliards - seulement en un an. Bien sûr, il existe des algorithmes plus rapides pour le calcul simple que le buste trivial utilisé dans mes devoirs, mais, en substance, cela ne change rien: après deux ou trois ordres de grandeur, la situation devient similaire.
Par conséquent, il serait bon d'avoir effectué une fois le travail de comptage, de stocker son résultat sous forme de tableau prêt à l'emploi et de l'utiliser au besoin.
En raison de l'évidence de l'idée, le réseau rencontre de nombreux liens vers des listes prédéfinies de nombres premiers déjà calculés par quelqu'un. Hélas, dans la plupart des cas, ils ne conviennent qu'à l'artisanat étudiant: l'un d'eux, par exemple, se promène de site en site et comprend 50 millions de simples. Ce montant ne peut qu'étonner les non-initiés: il a déjà été mentionné ci-dessus que sur un ordinateur personnel, en quelques heures, vous pouvez calculer indépendamment le tableau de tous les simples 32 bits, et il est quatre fois plus grand. Il y a environ 15 à 20 ans, une telle liste était en effet une réalisation héroïque pour la communauté laïque. Aujourd'hui, à l'ère des appareils multi-cœurs multi-gigahertz et multi-gigaoctets, ce n'est plus impressionnant.
J'ai eu la chance de me familiariser avec l'accès à un tableau beaucoup plus représentatif de tableaux simples, que j'utiliserai plus loin comme illustration et sacrifice pour mes expériences sur le terrain. Aux fins de complot, je l'appellerai 1TPrimo . Il contient tous les nombres premiers inférieurs à un billion.
En utilisant 1TPrimo comme exemple, il est facile de voir quels volumes vous devez gérer. Avec une capacité d'environ 37,6 milliards de valeurs au format entier 64 bits, cette liste est de 280 gigaoctets. Soit dit en passant - la partie de celui-ci qui pourrait tenir sur 32 chiffres ne représente que 0,5% du nombre de chiffres qui y sont représentés. Cela rend absolument clair que tout travail sérieux avec des nombres premiers tend inévitablement à des profondeurs de bits de 64 bits (ou plus).
Ainsi, la tendance sombre est évidente: une table de nombres premiers en quelque sorte sérieuse a inévitablement un volume titanesque. Et nous devons en quelque sorte lutter contre cela.
La première chose qui vient à l'esprit lorsque l'on regarde un tableau (Fig.2) est qu'il se compose de valeurs consécutives presque identiques qui ne diffèrent que par une ou deux des dernières décimales:
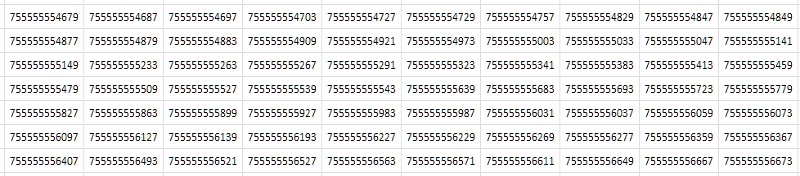
Simplement, à partir des considérations abstraites les plus générales: si le fichier contient beaucoup de données en double, il doit être bien compressé par l'archiveur. En effet, la compression de la table 1TPrimo avec l'utilitaire 7-zip populaire aux paramètres standard a donné un taux de compression assez élevé: 8,5. Certes, le temps de traitement - avec l'énorme taille de la table source - sur un serveur à 8 cœurs, avec une charge moyenne de tous les cœurs d'environ 80 à 90%, était de 14 heures 12 minutes. Les algorithmes de compression universels sont conçus pour des idées abstraites et généralisées sur les données. Dans certains cas particuliers, des algorithmes de compression spécialisés basés sur les caractéristiques bien connues de l'ensemble de données entrantes peuvent démontrer des indicateurs beaucoup plus efficaces, auxquels ce travail est consacré. Et son efficacité deviendra claire ci-dessous.
Les valeurs numériques proches des nombres premiers voisins demandent la décision de ne pas stocker ces valeurs elles-mêmes, mais les intervalles (différences) entre elles. Dans ce cas, des économies importantes peuvent être réalisées du fait que la profondeur de bits des intervalles est bien inférieure à la profondeur de bits des données initiales (Fig. 3).
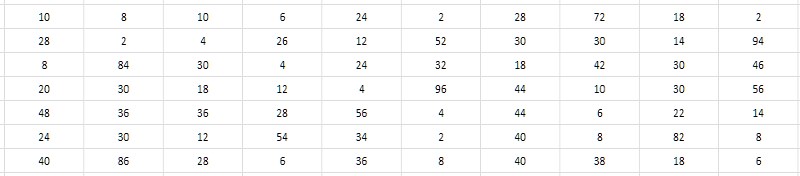
Et il semble que cela ne dépende pas de la profondeur de bits des simples générant l'intervalle. Une recherche exhaustive montre que les valeurs typiques des intervalles pour les nombres premiers pris à divers endroits dans la table 1TPrimo se situent dans les unités, les dizaines, parfois les centaines, et - comme première phrase de travail - ils pourraient probablement s'inscrire dans la plage de 8 bits entiers non signés, c'est-à-dire octets. Ce serait très pratique, et en comparaison avec le format 64 bits, cela conduirait immédiatement à une compression de données 8 fois - quelque part au niveau démontré par l'archiveur 7-zip. De plus, la simplicité des algorithmes de compression et de décompression devrait en principe avoir un impact majeur sur la vitesse de compression et d'accès aux données par rapport au 7-zip. Cela semble tentant.
Il est absolument clair que les données converties de leurs valeurs absolues en intervalles relatifs entre elles ne conviennent que pour restaurer une série de valeurs venant dans une rangée depuis le tout début de la table principale. Mais si nous ajoutons une structure d'index de bloc minimale à une telle table d'intervalles, alors avec des frais généraux supplémentaires insignifiants, cela nous permettra de restaurer - mais déjà bloc par bloc - à la fois l'élément de table par son numéro et l'élément le plus proche par une valeur définie arbitrairement, et ces opérations, ainsi que l'opération principale échantillons de séquence - en général, il épuise la part du lion des requêtes possibles sur ces données. Le traitement statistique, bien sûr, deviendra plus compliqué, mais il restera tout de même assez transparent, car il n'y a aucune astuce particulière pour le récupérer "à la volée" à partir des intervalles disponibles lors de l'accès au bloc de données requis.
Mais hélas. Une simple expérience numérique sur les données 1TPrimo montre que déjà à la fin des troisièmes dizaines de millions (c'est moins d'un centième de pour cent du volume 1TPrimo) - puis partout ailleurs - les intervalles entre les nombres premiers adjacents tombent régulièrement en dehors de la plage de 0..255.
Néanmoins, une expérience numérique légèrement compliquée révèle que la croissance de l'intervalle maximal entre les nombres premiers voisins avec la croissance de la table elle-même est très, très lente - ce qui signifie que l'idée est toujours bonne d'une certaine manière.
Le deuxième, plus attentif au tableau des intervalles, suggère qu'il est possible de stocker non pas la différence elle-même, mais sa moitié. Puisque tous les nombres premiers supérieurs à 2 sont évidemment impairs, respectivement, leurs différences sont évidemment égales. En conséquence, les différences peuvent être réduites de 2 sans perte de valeur; et pour être complet, on peut également soustraire un du quotient obtenu afin d'utiliser utilement la valeur zéro qui n'a pas été revendiquée autrement (figure 4). Une telle réduction des intervalles sera appelée ci-après monolithique, contrairement à la forme initiale lâche et poreuse, dans laquelle toutes les valeurs impaires et zéro se sont avérées non réclamées.
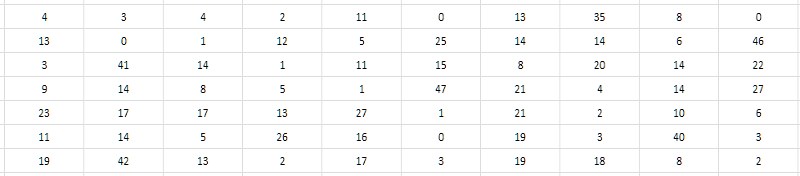
Il convient de noter que puisque l'intervalle entre les deux premiers simples (2 et 3) ne correspond pas à ce schéma, alors 2 devra être exclu du tableau des intervalles et garder ce fait à l'esprit tout le temps.
Cette technique simple vous permet de coder des intervalles de 2 à 512 dans la plage de valeurs 0..255. Encore une fois, l'espoir prend vie que la méthode de la différence nous permettra d'emballer une séquence beaucoup plus puissante de nombres premiers. Et à juste titre: une série de 37,6 milliards de valeurs présentées dans la liste 1TPrimo n'a révélé que 6 (six!) Intervalles qui ne sont pas dans la plage 2..512.
Mais c'était une bonne nouvelle; la mauvaise chose est que ces six intervalles sont dispersés assez librement sur la liste, et le premier d'entre eux se produit déjà à la fin du premier tiers de la liste, transformant les deux tiers restants en ballast impropre à cette méthode de compression (Fig.5):
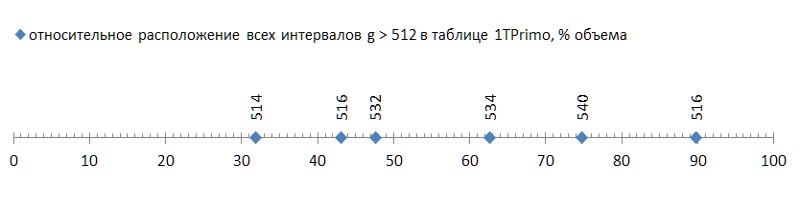
Un tel flush (quelques malheureux six pièces pour près de quarante milliards! - et sur vous ...) même avec une mouche dans la pommade à comparer - pour montrer l'honneur du goudron. Mais hélas, c'est un modèle, pas un accident. Si l'on trace la première apparition d'intervalles entre les nombres premiers en fonction de la longueur des données, il devient clair que ce phénomène réside dans la génétique des nombres premiers, bien qu'il progresse extrêmement lentement (Fig. 6 *).
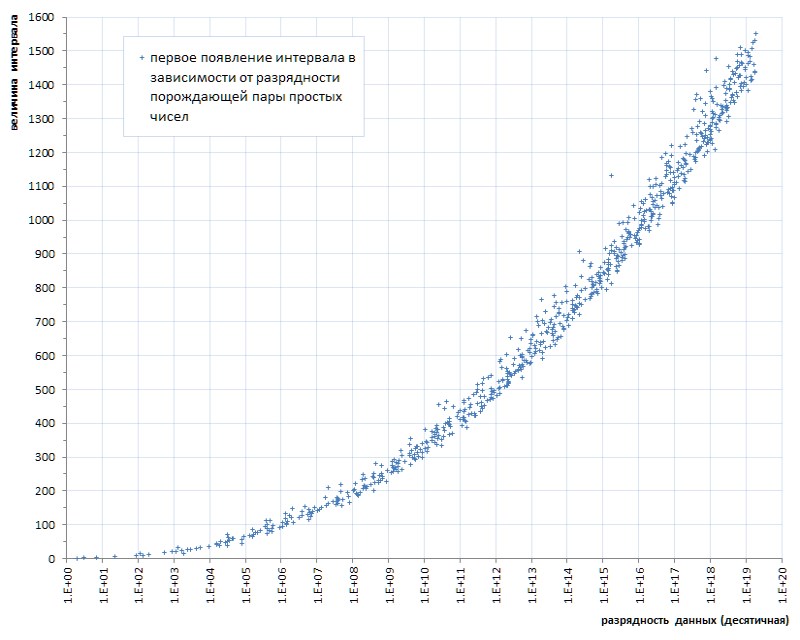
* Calendrier compilé selon le site thématique de Thomas R. Nisley ,
qui sont plusieurs ordres de grandeur supérieurs à la puissance de la liste 1TPrimo
Mais même cette progression très lente laisse entendre sans ambiguïté: on ne peut se limiter à une certaine profondeur de bits prédéterminée d'un intervalle qu'à une certaine puissance prédéterminée de la liste. Autrement dit, il ne convient pas comme solution universelle.
Cependant, le fait que la méthode proposée de compression d'une séquence de nombres premiers vous permette d'implémenter une table compacte simple avec une capacité de près de 12 milliards de valeurs est déjà tout à fait un résultat. Une telle table occupe un volume de 11,1 gigaoctets - contre 89,4 gigaoctets dans un format trivial 64 bits. Certes, pour un certain nombre d'applications, une telle solution peut être suffisante.
Et ce qui est intéressant: la procédure de traduction d'une table 1TPrimo 64 bits au format d'intervalles 8 bits avec une structure de bloc, en utilisant un seul cœur de processeur (pour la parallélisation, vous devrez recourir à une complication importante du programme, et cela n'en valait absolument pas la peine) et pas plus de 5 % de la charge du processeur (la plupart du temps consacré aux opérations sur les fichiers) n'a pris que 19 minutes Contre - je me souviens - 14 heures sur huit cœurs à 80-90% de la charge dépensée par l'archiveur 7-zip.
Bien sûr, seul le premier tiers du tableau a été soumis à cette traduction, dans laquelle la plage d'intervalles ne dépasse pas 512. Par conséquent, si nous apportons les 14 heures complètes au même tiers, alors 19 minutes doivent être comparées à près de 5 heures de l'archiveur 7-zip. Avec une quantité comparable de compression (8 et 8,5), la différence est environ 15 fois. Étant donné que la part du lion du temps de travail du programme de diffusion était occupée par les opérations de fichiers, la différence serait encore plus accentuée sur un système de disque plus rapide. Et intellectuellement, le temps de fonctionnement de 7-zip sur huit cœurs doit toujours être compté sur un seul thread, puis la comparaison deviendra vraiment adéquate.
La sélection dans une telle base de données diffère très peu dans le temps de la sélection dans la table des données décompressées et est presque entièrement déterminée par le temps des opérations sur les fichiers. Les nombres spécifiques dépendent fortement du matériel spécifique, sur mon serveur, en moyenne, l'accès à un bloc de données arbitraire a pris 37,8 μs, tandis que la lecture séquentielle des blocs - 4,2 μs par bloc, pour un déballage complet du bloc - moins de 1 μs. Autrement dit, cela n'a aucun sens de comparer la décompression des données avec le travail d'un archiveur standard. Et c'est un gros plus.
Et, enfin, les observations offrent une autre troisième solution qui supprime toute restriction sur la puissance des données: des intervalles de codage avec des valeurs de longueur variable. Cette technique est depuis longtemps largement utilisée dans les applications liées à la compression. Sa signification est que si l'on trouve dans l'entrée que certaines valeurs sont souvent trouvées, certaines sont moins courantes et certaines sont très rares, alors nous pouvons coder le premier avec des codes courts, le second avec des codes plus authentiques et le troisième - très long (peut-être même très long, car peu importe: tout de même, de telles données sont très rares). Par conséquent, la longueur totale des codes reçus peut être beaucoup plus courte que les données d'entrée.
En examinant déjà le graphique de l'apparence des intervalles de la figure 7, nous pouvons faire l'hypothèse que si les intervalles sont 2, 4, 6, etc. apparaissent plus tôt que les intervalles, disons 100, 102, 104, etc., alors les premiers devraient continuer à se produire beaucoup plus souvent que les seconds. Et vice versa - si les intervalles 514 ne se présentent qu'à partir de 11,99 milliards, 516 - à partir de 16,2 milliards et 518 - à partir de seulement 87,7 milliards, ils ne se rencontreront que très rarement. C'est-à-dire que, a priori, nous pouvons supposer la relation inverse entre la taille de l'intervalle et sa fréquence dans une séquence de nombres premiers. Et cela signifie - vous pouvez construire une structure simple qui implémente des codes de longueur variable pour eux.
Bien entendu, les statistiques sur la fréquence des intervalles devraient devenir déterminantes pour le choix d'une méthode de codage particulière. Heureusement, contrairement aux données arbitraires, la fréquence des intervalles entre les nombres premiers - qui en eux-mêmes sont une séquence donnée déterminée une fois pour toutes - est également une caractéristique définie une fois pour toutes et strictement déterminée.
La figure 7 montre la réponse en fréquence des intervalles pour l'ensemble de la liste 1TPrimo:
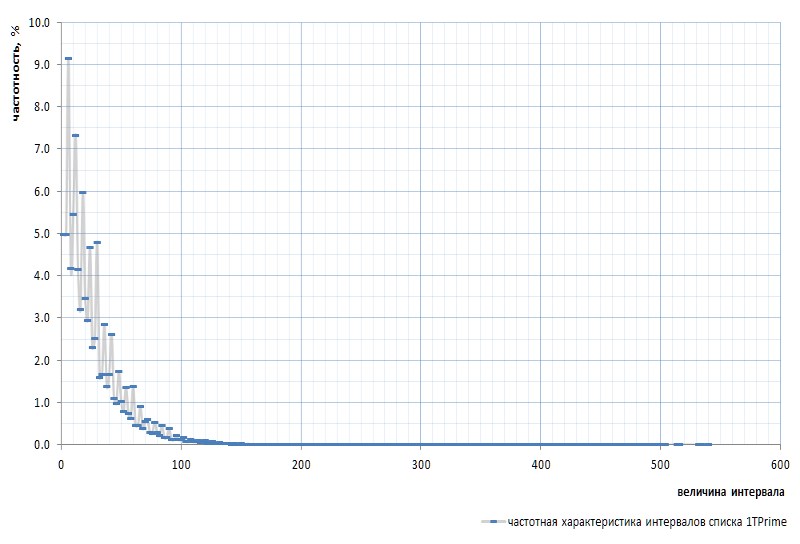
Ici, il est nécessaire de mentionner à nouveau que l'intervalle entre les tout premiers nombres premiers 2 et 3 est exclu du graphique: cet intervalle est 1 et se produit exactement une fois dans la séquence des nombres premiers, quelle que soit la puissance de la liste. Cet intervalle est si particulier qu'il est plus facile de supprimer 2 de la liste des simples que de s'égarer constamment dans les réservations. Le sim est déclaré que le nombre 2 est un nombre premier virtuel : il n'est pas visible dans les listes, mais il est là. Comme ce gopher.
À première vue, le graphique des fréquences confirme pleinement l'hypothèse a priori donnée par quelques paragraphes ci-dessus. Il montre clairement l'hétérogénéité statistique des intervalles et la fréquence élevée des petites valeurs par rapport aux grandes. Cependant, dans la deuxième vue, plus convexe, le graphique s'avère beaucoup plus intéressant (Fig.8):
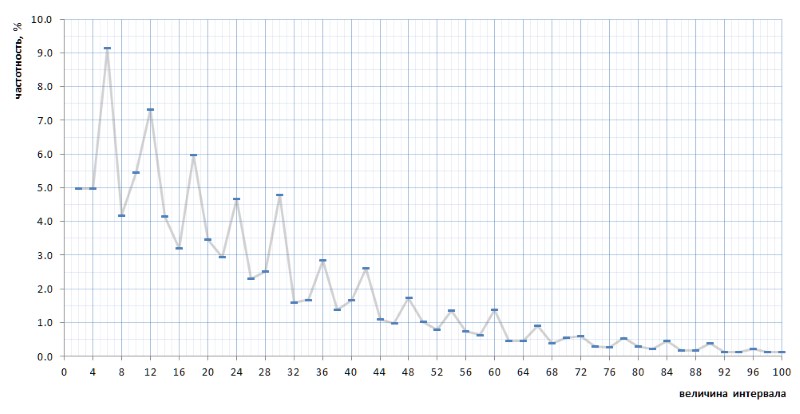
De façon assez inattendue, il s'avère que les intervalles les plus fréquents ne sont pas 2 et 4, comme cela semblait provenir de considérations générales, mais 6, 12 et 18, suivis de 10 - et seulement ensuite 2 et 4 avec une fréquence presque égale (différence en 7 chiffres après le point décimal). Et en outre, la multiplicité des valeurs de crête du nombre 6 est tracée dans tout le graphique.
Encore plus intéressant, cette nature révélée par inadvertance du graphique est universelle - et, dans tous les détails, avec tous ses défauts - sur toute la séquence d'intervalles simples représentée par la liste 1TPrimo, il est probable qu'elle soit universelle pour toute séquence d'intervalles simples (bien sûr, une telle déclaration audacieuse a besoin de preuves, que je transmets avec grand plaisir aux épaules des spécialistes de la théorie des nombres). La figure 10 montre une comparaison des statistiques d'intervalle complet (ligne écarlate) avec des échantillons à intervalle limité prélevés à plusieurs endroits arbitraires de la liste 1TPrimo (lignes d'autres couleurs):
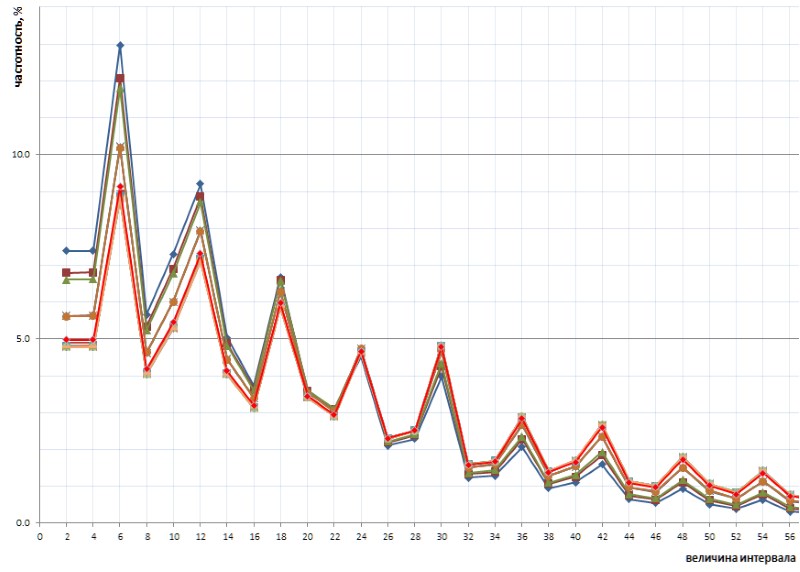
On peut voir sur ce graphique que tous ces échantillons se répètent exactement, avec seulement une légère différence dans les parties gauche et droite de la figure: ils semblent être légèrement tournés dans le sens antihoraire autour du point d'intervalle avec une valeur de 24. Cette rotation est probablement due au fait que le plus haut dans la gauche des parties des graphiques sont construites sur des échantillons avec des profondeurs de bits plus faibles. Dans de tels échantillons, il n'y en a pas encore du tout, ou de grands intervalles sont rares, qui deviennent fréquents dans les échantillons avec des profondeurs de bits plus élevées. En conséquence, leur absence est en faveur de la fréquence des intervalles avec des valeurs plus faibles. Dans les échantillons avec des profondeurs de bits plus élevées, de nombreux nouveaux intervalles avec de grandes valeurs apparaissent; par conséquent, la fréquence des intervalles plus petits diminue légèrement. Très probablement, le point de pivot, avec une augmentation de la puissance de la liste, se déplacera vers des valeurs plus grandes. Quelque part, à côté, se trouve le point d'équilibre du graphique, où la somme de toutes les valeurs à droite est approximativement égale à la somme de toutes les valeurs à gauche.
Cette nature intéressante de la fréquence des intervalles suggère d'abandonner la structure triviale des codes de longueur variable. Typiquement, une telle structure se compose d'un paquet de bits de différentes longueurs et fins. Par exemple, vient d'abord un certain nombre de bits de préfixe définis sur une valeur spécifique, par exemple 0. Il y a un bit d'arrêt derrière eux, qui devrait indiquer l'achèvement du préfixe et, par conséquent, devrait différer du préfixe: 1 dans ce cas. Le préfixe peut ne pas avoir de longueur, c'est-à-dire que l'échantillonnage peut commencer immédiatement avec un bit d'arrêt, déterminant ainsi la séquence la plus courte. Le bit d'arrêt est généralement suivi d'un suffixe, dont la longueur est déterminée d'une manière prédéterminée par la longueur du préfixe. , , — . , - . - (, , - ) , .
, .
Et ici, une chose plus importante doit être déclarée. À première vue, la cyclicité observée implique la division des intervalles en triples: {2,4, 6 } , {8,10, 12 } , {14,16, 18 } et ainsi de suite (les valeurs avec la fréquence maximale dans chaque triple sont marquées en gras) . Cependant, en fait, le cycle ici est légèrement différent.
Je ne citerai pas toute la ligne de raisonnement, qui, en fait, n'est pas là: c'était une supposition intuitive, complétée par une méthode d'énumération brutale des options, des calculs et des échantillons qui prenait plusieurs jours par intermittence. La cyclicité révélée à la suite consiste en six intervalles {2,4, 6 ,8,10, 12 } , {14,16, 18 ,20,22, 24 } , {26,28, 30 ,32,34, 36 } et ainsi de suite (les intervalles de fréquence maximale sont à nouveau mis en évidence en gras).
En un mot, l'algorithme de conditionnement proposé est le suivant.
La division des intervalles en six nombres pairs nous permet de représenter tout intervalle g sous la forme g = i * 12 + t , où i est l'indice des six auxquels appartient cet intervalle ( i = {0,1,2,3, ...} ) et t est une queue représentant l'une des valeurs d'une définition rigide, bornée et identique pour six quelconques de l'ensemble {2,4,6,8,10,12} . La réponse en fréquence de l'indice mis en évidence ci-dessus est presque exactement inversement proportionnelle à sa valeur, il est donc logique de convertir les six indices en une structure triviale d'un code de longueur variable, dont un exemple est donné ci-dessus. Les caractéristiques de fréquence de la pince vous permettent de la diviser en deux groupes qui peuvent être encodés avec des chaînes de bits de longueurs différentes: les valeurs 6 et 12, qui sont le plus souvent trouvées, sont encodées avec un bit, les valeurs 2, 4, 8 et 10, que l'on rencontre beaucoup moins fréquemment, sont encodées avec deux bits. Bien sûr, un bit de plus est nécessaire pour distinguer ces deux options.
Un tableau contenant des paquets de bits est complété par des champs fixes qui spécifient les valeurs de départ des données présentées dans le bloc, et d'autres quantités nécessaires pour restaurer un simple arbitraire ou une séquence de simples à partir des intervalles stockés dans le bloc.
En plus de cette structure d'index de bloc, l'utilisation de codes de longueur variable est compliquée par les coûts supplémentaires par rapport aux intervalles à bits fixes.
Lorsque vous utilisez des intervalles de taille fixe, déterminer le bloc dans lequel rechercher un nombre premier par son numéro de série est une tâche assez simple, car le nombre d'intervalles par bloc est connu à l'avance. Mais la recherche d'une solution simple à la valeur la plus proche n'a pas de solution directe. Alternativement, vous pouvez utiliser une formule empirique qui vous permet de trouver le numéro de bloc approximatif avec l'intervalle requis, après quoi vous devrez rechercher le bloc souhaité par une recherche exhaustive.
Pour une table avec des codes de longueur variable, la même approche est requise pour les deux tâches: à la fois pour récupérer une valeur par nombre et pour rechercher par valeur. Comme la longueur des codes varie, on ne sait jamais à l'avance combien de différences sont stockées dans un bloc particulier, et dans quel bloc se trouve la valeur souhaitée. Il a été déterminé expérimentalement qu'avec une taille de bloc de 512 octets (qui inclut certains octets d'en-tête), la capacité du bloc peut aller jusqu'à 10-12 pour cent de la valeur moyenne. Des blocs plus petits donnent une dispersion relative encore plus grande. Dans le même temps, la valeur moyenne de la capacité du bloc lui-même a tendance à diminuer lentement à mesure que la table grandit. La sélection de formules empiriques pour une détermination imprécise du bloc initial pour rechercher la valeur souhaitée à la fois en nombre et en valeur est une tâche non triviale. Vous pouvez également utiliser une indexation plus complexe et sophistiquée.
En fait, c'est tout.
Ci-dessous, les subtilités de compression d'une table principale utilisant des codes de longueur variable et les structures qui lui sont associées sont décrites de manière plus formelle et détaillée, et le code des fonctions d'emballage et de déballage des intervalles en C est donné.
Le résultat.
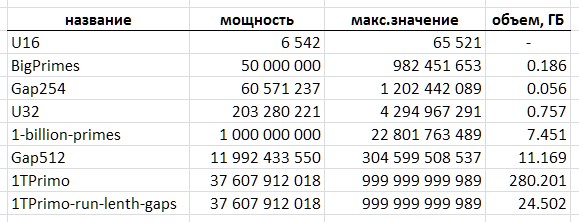
La quantité de données converties du tableau 1TPrimo en codes de longueur variable, complétée par une structure d'index de bloc, également décrite ci-dessous, s'élève à 26309295104 octets (24,5 Go), c'est-à-dire que le taux de compression atteint 11,4. De toute évidence, avec l'augmentation de la profondeur de bits, le taux de compression augmentera.
Le temps de diffusion de 280 Go de la table 1TPrimo dans le nouveau format était de 1 heure. C'est le résultat attendu après des expériences avec des intervalles de compression en entiers à un octet. Dans les deux cas, la traduction de la table source se compose principalement d'opérations sur les fichiers et ne charge presque pas le processeur (dans le second cas, la charge est toujours plus élevée en raison de la complexité de calcul plus élevée de l'algorithme). Le temps d'accès aux données n'est pas non plus très différent des intervalles à un octet, mais le temps de décompresser un bloc complet de la même taille a pris 1,5 μs, en raison de la complexité plus élevée de l'algorithme d'extraction des codes de longueur variable.
Le tableau (Fig. 10) résume les caractéristiques volumétriques des tableaux de nombres premiers mentionnés dans ce texte.
Description de l'algorithme de compression
Termes et notation
P (prime): P1=3, P2=5, P3=7 ... Pn, Pn1 sont des nombres premiers en fonction de leurs numéros de série. Encore une fois (et pour la dernière fois), je souligne que
P0=2 est un nombre premier virtuel; par souci d'uniformité formelle, ce nombre est physiquement exclu de la liste des nombres premiers.
G (gap) - l'intervalle entre deux nombres premiers consécutifs Gn = Pn1 - Pn; G={2,4,6,8 ...} Gn = Pn1 - Pn; G={2,4,6,8 ...} .
D (dense) - réduit à un intervalle de forme monolithique: D = G/2 -1; D={0,1,2,3 ...} D = G/2 -1; D={0,1,2,3 ...} . Les six intervalles sous la forme monolithique ressemblent à {0,1,2,3,4,5}, {6,7,8,9,10,11}, {12,13,14,15,16,17} etc.
Q (quotient) - indice des six réduit à une forme monolithique, Q = D div 6; Q={0,1,2,3 ...} Q = D div 6; Q={0,1,2,3 ...}
R (remainder) - le reste des six monolithiques R = D mod 6. R toujours une valeur dans la plage {0,1,2,3,4,5} .
Les valeurs Q et R obtenues par la méthode ci-dessus à partir de tout intervalle arbitraire G , en raison de leurs caractéristiques de fréquence stables, sont soumises à la compression et au stockage sous la forme de paquets de bits de longueur variable, décrits ci-dessous. Les chaînes de bits codant les valeurs Q et R dans un paquet sont créées de différentes manières: pour coder l'index Q , la chaîne de bits du préfixe H , le flux F et le bit auxiliaire S , et le groupe de bits de l'infixe X et le bit auxiliaire A sont utilisés pour coder le reste R
A (arbiter) - un bit qui détermine la taille de l'infixe X : 0 - infixe un bit, 1 - deux bits.
X (infix) - Infixe à 1 ou 2 bits, avec le bit d'arbitre R tabulaire (le tableau montre également la fréquence des six premiers avec de tels infixes pour référence):
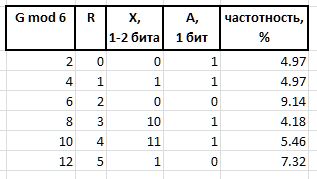
F (fluxion) est une fluxion, une dérivée de l'indice Q longueur variable L={0,1,2...} , conçue pour distinguer la sémantique des chaînes de bits (), 0, 00, 000, ou 1, 01, 001 , etc. d.
Une chaîne de bits d'unités de longueur L est exprimée par 2^L - 1 (le signe ^ signifie exponentiation). En notation C, la même valeur peut être obtenue par l'expression 1<<L - 1 . La valeur de fluxia de longueur L peut alors être obtenue à partir de Q expression
F = Q - (1 << L - 1),
et restaurer Q de fluxia par expression
Q = (1 << L - 1) + F.
Par exemple, pour les quantités Q = {0..15} , les chaînes de bits Fluxia suivantes seront obtenues:
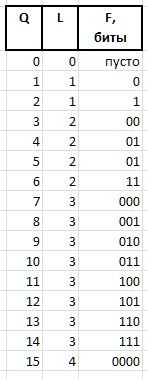
Les deux derniers champs de bits nécessaires pour compresser / restaurer les valeurs sont:
H (header) - préfixe, une chaîne de bits définie sur 0.
S (stop) - bit d'arrêt mis à 1, terminant le préfixe.
En fait, ces bits sont traités d'abord dans des chaînes de bits, ils vous permettent de déterminer lors du déballage ou de définir lors de l'emballage la taille du flux et le début de l'arbitre et des champs de flux - immédiatement après le bit d'arrêt.
W (width) - la largeur de tout le code en bits.
La structure complète du paquet de bits est représentée sur la figure 11:
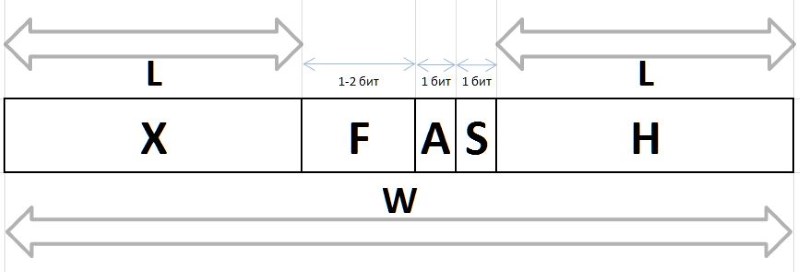
Les valeurs de Q et R récupérées à partir de ces chaînes nous permettent de restaurer la valeur initiale de l'intervalle:
D = Q * 6 + R,
G = (D + 1) * 2,
et la séquence d'intervalles restaurés vous permet de restaurer les nombres premiers d'origine à partir d'une valeur de base donnée du bloc (bloc d'intervalles initial) en y ajoutant tous les intervalles de ce bloc en séquence.
Pour travailler avec des chaînes de bits, une variable entière de 32 bits est utilisée, dans laquelle les bits les moins significatifs sont traités et après les avoir utilisés, les bits sont décalés vers la gauche lors du compactage ou vers la droite lors du décompactage.
Structure des blocs
En plus des chaînes de bits, un bloc contient les informations nécessaires pour extraire ou ajouter des bits, ainsi que pour déterminer le contenu d'un bloc.
// // typedef unsigned char BYTE; typedef unsigned short WORD; typedef unsigned int LONG; typedef unsigned long long HUGE; typedef int BOOL; #define TRUE 1 #define FALSE 0 #define BLOCKSIZE (256) // : , #define HEADSIZE (8+8+2+2+2) // , #define BODYSIZE (BLOCKSIZE-HEADSIZE) // . // typedef struct { HUGE base; // , HUGE card; // WORD count; // WORD delta; // base+delta = WORD offset; // BYTE body[BODYSIZE]; // } crunch_block; // , put() get() crunch_block block; // . // NB: len/val rev/rel // , , // . static struct tail_t { BYTE len; // S A BYTE val; // , A - S BYTE rev; // BYTE rel; // } tails[6] = { { 4, 3, 2, 3 }, { 4, 7, 5, 3 }, { 3, 1, 0, 4 }, { 4,11, 1, 4 }, { 4,15, 3, 4 }, { 3, 5, 4, 4 } }; // BOOL put(int gap) { // 1. int Q, R, L; // (), (), int val = gap / 2 - 1; Q = val / 6; R = val % 6; L = -1; // .., 0 - 1 val = Q + 1; while (val) { val >>= 1; L++; } // L val = Q - (1 << L) + 1; // val <<= tails[R].len; val += tails[R].val; // val <<= L; // L += L + tails[R].len; // // 2. val L buffer put_index if (block.offset + L > BODYSIZE * 8) // ! return FALSE; Q = (block.offset / 8); // , R = block.offset % 8; // block.offset += L; // block.count++; // block.delta += gap; if (R > 0) // { val <<= R; val |= block.body[Q]; L += R; } // L = L / 8 + ((L % 8) > 0 ? 1 : 0); // while (L-- > 0) { block.body[Q++] = (char)val; val >>= 8; } return TRUE; } // int get_index; // // int get() { if (get_index >= BODYSIZE * 8) return 0; // int val = *((int*)&block.body[get_index / 8]) >> get_index % 8; // 4 if (val == 0) return -1; // ! int Q, R, L, F, M, len; // , , , , L = 0; while (!(val & 1)) { val >>= 1; L++; } // - if ((val & 3) == 1) // R = (val >> 2) & 1; // else R = ((val >> 2) & 3) + 2; // len = tails[R].rel; get_index += 2 * L + len; val >>= len; M = ((1 << L) - 1); // F = val & M; // Q = F + M; // return 2 * (1 + (6 * Q + tails[R].rev)); // }
Améliorations
Si nous alimentons la base d'intervalles obtenue au même archiveur 7 zip, puis en une heure et demie de travail intensif sur un serveur 8 cœurs, il parvient à compresser le fichier d'entrée de près de 5%. Autrement dit, dans la base de données d'intervalles de longueur variable du point de vue de l'archiveur, il y a encore une certaine redondance. Il y a donc lieu de spéculer un peu (dans le bon sens du terme) sur le thème de la réduction supplémentaire de la redondance des données.
Le déterminisme fondamental de la séquence d'intervalles entre les nombres premiers permet de faire des calculs exacts de l'efficacité de codage par une méthode ou une autre. En particulier, de petits croquis (plutôt chaotiques) ont permis de tirer une conclusion fondamentale sur les avantages du codage des six sur les triplets, et sur les avantages de la méthode proposée sur les codes triviaux de longueur variable (Fig.12):
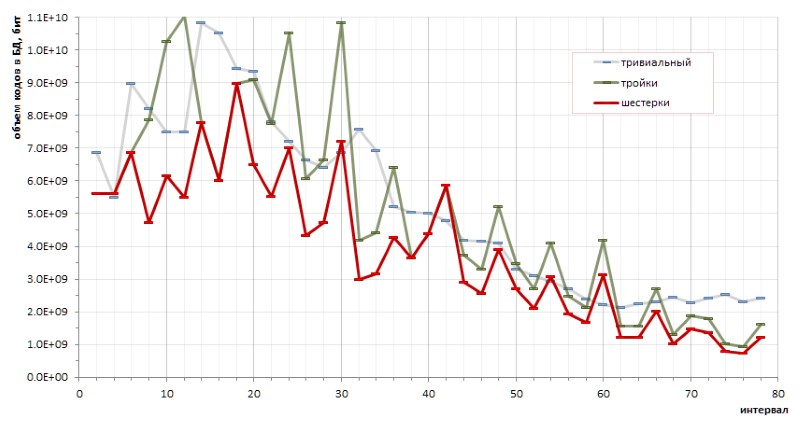
Cependant, les hauts ennuyeux du graphique rouge suggèrent de manière transparente qu'il peut y avoir d'autres méthodes de codage qui rendraient le graphique encore plus doux.
Une autre direction suggère de vérifier la fréquence des intervalles consécutifs. À partir de considérations générales: étant donné que les intervalles 6, 12 et 18 sont les plus courants dans une population de nombres premiers, alors ils sont susceptibles d'être plus souvent trouvés en paires (doublets), triplets (triplets) et les combinaisons similaires d'intervalles. Si la répétabilité des doublons (et peut-être même des triplets ... enfin, tout d'un coup!) S'avère statistiquement significative dans la masse totale des intervalles, alors il est logique de les traduire dans un code séparé.
L'expérience à grande échelle révèle une certaine prédominance des doublets individuels sur les autres. Cependant, si le leadership absolu est attendu pour la paire (6,6) - 1,37% de tous les doublets - alors les autres gagnants de cette note sont beaucoup moins évidents:
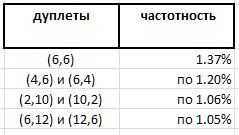
Et, comme le doublet (6,6) symétrique, et que tous les autres doublets notés sont asymétriques et se retrouvent dans le classement par doubles miroir avec la même fréquence, il semble que le record d'enregistrement du doublet (6,6) dans cette série devrait être divisé en deux entre les doubles indiscernables (6,6) et (6,6) , ce qui les place à 0,68% loin de la frontière du palmarès. Et cela confirme une fois de plus l'observation qu'aucune supposition vraie sur les nombres premiers ne peut se produire sans surprises.
Les statistiques des triplets démontrent également le leadership de ces triplets d'intervalles, qui ne correspondent pas tout à fait à l'hypothèse spéculative partant de la fréquence la plus élevée des intervalles 6, 12, 18. Par ordre décroissant de popularité, les leaders de fréquence parmi les triplets se présentent comme suit:

etc.
Je crains cependant que les résultats de mes spéculations intéressent moins les programmeurs que les mathématiciens, peut-être à cause des corrections inattendues apportées par la pratique aux suppositions intuitives. Il est peu probable qu'il soit possible de tirer un dividende substantiel du pourcentage de fréquence mentionné en faveur d'une nouvelle augmentation du taux de compression, tandis que la complexité de l'algorithme menace de croître de manière très significative.
Limitations
Il a déjà été noté plus haut que l'augmentation de la valeur maximale des intervalles en relation avec la capacité des nombres premiers est très, très lente. En particulier, on peut voir sur la figure 6 que l'intervalle entre les nombres premiers qui peuvent être représentés au format d'un entier non signé 64 bits sera évidemment inférieur à 1600.
L'implémentation décrite vous permet d'empaqueter et de décompresser correctement toutes les valeurs d'intervalle de 18 bits (en fait, la première erreur d'empaquetage se produit avec un intervalle d'entrée de 442358). Je n'ai pas assez d'imagination pour supposer que la base de données des intervalles premiers peut atteindre de telles valeurs: au départ, elle se situe aux alentours de 100 bits et pour calculer plus précisément la paresse. En cas d'incendie, il n'est pas toujours difficile d'élargir la plage d'intervalles.
Merci d'avoir lu cet endroit :)