
Nouveau langage en Data Science. Julia est une langue assez rare en Russie, bien qu'elle soit utilisée à l'étranger depuis 5 ans (ils m'ont aussi surpris). Il n'y a pas de sources en russe, j'ai donc décidé de citer l'exemple de Julia, tiré d'un merveilleux livre. La meilleure façon d'apprendre une langue est de commencer à y écrire quelque chose.
Et pour que cela attire également l'attention, utilisez l'apprentissage automatique.Bonjour habrozhitelam.
Il y a quelque temps, j'ai commencé à apprendre la nouvelle langue de Julia. Eh bien, comme neuf. C'est quelque chose entre Matlab et Python, la syntaxe est très similaire et le langage lui-même est écrit en C / C ++. En général, l'histoire de la création, quoi, pourquoi et pourquoi est sur Wikipédia et dans quelques articles sur Habré.
La première chose qui a commencé mon étude de la langue - à droite, le
cours en
ligne Google on Coursera google en anglais. Là, sur la syntaxe de base +, un mini-projet sur la prédiction des maladies en Afrique est écrit en parallèle. Bases et pratique immédiatement. Si vous avez besoin d'un certificat, achetez la version complète. Je suis allé gratuitement. La différence entre cette version est que personne ne vérifiera vos tests et DZ. Il était plus important pour moi de faire connaissance qu'un certificat. (Lire 50 dollars coincés)
Après cela, j'ai décidé de lire un livre sur Julia. Google a publié une liste de livres et a étudié les critiques et les critiques, en a choisi un et a commandé sur Amazon. Les versions de livres sont toujours plus agréables à lire et à dessiner au crayon.
Le livre s'appelle
Julia for Data Science par Zacharias Voulgaris, PhD. L'extrait que je veux présenter contient de nombreuses fautes de frappe dans le code que j'ai corrigé et présentera donc la version de travail + mes résultats.
kNN
Ceci est un exemple d'application de l'algorithme de classification pour la méthode des voisins les plus proches. Probablement l'un des plus anciens algorithmes d'apprentissage automatique. L'algorithme n'a pas de phase d'apprentissage et est assez rapide. Sa signification est assez simple: pour classer un nouvel objet, vous devez trouver des "voisins" similaires dans l'ensemble de données (base de données), puis déterminer la classe en votant.
Je réserverai tout de suite que Julia a des forfaits prêts à l'emploi, et il est préférable de les utiliser pour réduire le temps et les erreurs. Mais ce code est, en quelque sorte, indicatif de la syntaxe Julia. C’est plus pratique pour moi d’apprendre une nouvelle langue par des exemples que de lire des extraits secs de la forme générale d’une fonction.
Donc, ce que nous avons à l'entrée:
Données d' apprentissage
X (échantillon d'apprentissage),
étiquettes de données d'apprentissage x (étiquettes correspondantes),
données de test Y (sélection de test),
nombre de voisins k (nombre de voisins).
Vous aurez besoin de 3 fonctions: fonction de
calcul de distance, fonction de classification et
principale .
La ligne de fond est la suivante: prendre un élément du tableau de test, calculer la distance de celui-ci aux éléments du tableau d'apprentissage. Ensuite, nous sélectionnons les indices de ces
k éléments qui se sont avérés être aussi proches que possible. Nous attribuons l'élément testé à la classe la plus courante parmi les
k voisins les plus proches.
function CalculateDistance{T<:Number}(x::Array{T,1}, y::Array{T,1}) dist = 0 for i in 1:length(x) dist += (x[i] - y[i])^2 end dist = sqrt(dist) return dist end
La fonction principale de l'algorithme. La matrice des distances entre les objets des échantillons d'apprentissage et de test, les étiquettes de l'ensemble d'apprentissage et le nombre de "voisins" les plus proches vient à l'entrée. Le résultat est les étiquettes prévues pour les nouveaux objets et les probabilités de chaque étiquette.
function Classify{T<:Any}(distances::Array{Float64,1}, labels::Array{T,1}, k::Int) class = unique(labels) nc = length(class) #number of classes indexes = Array(Int,k) #initialize vector of indexes of the nearest neighbors M = typemax(typeof(distances[1])) #the largest possible number that this vector can have class_count = zeros(Int, nc) for i in 1:k indexes[i] = indmin(distances) #returns index of the minimum element in a collection distances[indexes[i]] = M #make sure this element is not selected again end klabels = labels[indexes] for i in 1:nc for j in 1:k if klabels[j] == class[i] class_count[i] +=1 end end end m, index = findmax(class_count) conf = m/k #confidence of prediction return class[index], conf end
Et bien sûr, toutes les fonctions.
Nous aurons un ensemble d'apprentissage
X à l'entrée, un ensemble d'apprentissage marque
x , un ensemble d'essai
Y et le nombre de «voisins»
k .
En sortie, nous recevrons les labels prédits et les probabilités correspondantes d'attribution de chaque classe.
function main{T1<:Number, T2<:Any}(X::Array{T1,2}, x::Array{T2,1}, Y::Array{T1,2}, k::Int) N = size(X,1) n = size(Y,1) D = Array(Float64,N) #initialize distance matrix z = Array(eltype(x),n) #initialize labels vector c = Array(Float64, n) #confidence of prediction for i in 1:n for j in 1:N D[j] = CalculateDistance(X[j,:], vec(Y[i,:])) end z[i], c[i] = Classify(D,x,k) end return z, c end
Test
Testons ce que nous avons. Pour plus de commodité, nous enregistrons l'algorithme dans le fichier kNN.jl.
La base est empruntée au cours
Open Machine Learning . L'ensemble de données s'appelle Samsung Human Activity Recognition. Les données proviennent des accéléromètres et des gyroscopes des téléphones mobiles Samsung Galaxy S3, et le type d'activité d'une personne avec un téléphone dans sa poche est également connu - qu'il marche, se tienne, s'allonge, s'assied ou monte / descend les escaliers. Nous allons résoudre le problème de la détermination précise du type d'activité physique en tant que problème de classification.
Les balises correspondront aux éléments suivants:
1 - marcher
2 - monter les escaliers
3 - en bas des escaliers
4 - siège
5 - une personne se tenait à ce moment
6 - la personne mentait
include("kNN.jl") training = readdlm("samsung_train.txt"); training_label = readdlm("samsung_train_labels.txt"); testing = readdlm("samsung_test.txt"); testing_label = readdlm("samsung_test_labels.txt"); training_label = map(Int, training_label) testing_label = map(Int, testing_label) z = main(training, vec(training_label), testing, 7) n = length(testing_label) println(sum(testing_label .== z[1]) / n)
Résultat: 0.9053274516457415La qualité est évaluée par le rapport des objets correctement prédits à l'échantillon de test entier. Cela ne semble pas si mal. Mais mon objectif est plutôt de montrer Julia, et qu'il a sa place dans la Data Science.
Visualisation
Ensuite, je voulais essayer de visualiser les résultats de la classification. Pour ce faire, vous devez créer une image en deux dimensions, comportant 561 signes et ne sachant pas lesquels sont les plus importants. Par conséquent, pour réduire la dimensionnalité et la conception de données subséquentes sur le sous-espace orthogonal d'entités, il a été décidé d'utiliser l'
analyse en composantes principales (ACP). En Julia, comme en Python, il y a des packages prêts à l'emploi, donc on simplifie un peu notre vie.
using MultivariateStats #for PCA A = testing[1:10,:] #PCA for A M_A = fit(PCA, A'; maxoutdim = 2) Jtr_A = transform(M_A, A'); #PCA for training M = fit(PCA, training'; maxoutdim = 2) Jtr = transform(M, training'); using Gadfly #shows training points and uncertain point pl1 = plot(training, layer(x = Jtr[1,:], y = Jtr[2,:],color = training_label, Geom.point), layer(x = Jtr_A[1,:], y = Jtr_A[2,:], Geom.point)) #predicted values for uncertain points from testing data z1 = main(training, vec(training_label), A, 7) pl2 = plot(training, layer(x = Jtr[1,:], y = Jtr[2,:],color = training_label, Geom.point), layer(x = Jtr_A[1,:], y = Jtr_A[2,:],color = z[1], Geom.point)) vstack(pl1, pl2)
Dans la première figure, l'ensemble d'apprentissage et plusieurs objets de l'ensemble de test sont marqués, qui devront être attribués à leur classe. En conséquence, la deuxième figure montre que ces objets ont été marqués.

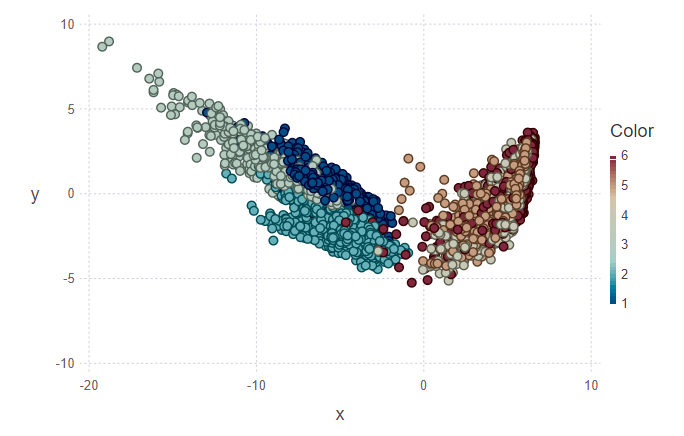
println(z[1][1:10], z[2][1:10]) > [5, 5, 5, 5, 5, 5, 5, 5, 5, 4][1.0, 0.888889, 0.888889, 0.888889, 1.0, 1.0, 1.0, 1.0, 0.777778, 0.555556]
En regardant les images, je veux poser la question «pourquoi ces grappes sont-elles laides?». Je vais vous expliquer. Les grappes individuelles ne sont pas très clairement délimitées en raison de la nature des données et de l'utilisation de l'ACP. Pour le PCA, marcher et monter des escaliers est comme une classe - la classe de mouvement. En conséquence, la deuxième classe est la classe de repos (assise, debout, couchée, qui ne se distingue pas beaucoup entre elles). Et donc, une séparation claire peut être tracée en deux classes au lieu de six.
Conclusion
Pour moi, ce n'est qu'une première immersion dans Julia et l'utilisation de ce langage dans le machine learning. Soit dit en passant, dans lequel je suis aussi plus probablement un amateur qu'un professionnel. Mais même si je suis intéressé, je continuerai d'étudier cette question plus en profondeur. De nombreuses sources étrangères parient sur Julia. Eh bien, attendez et voyez.
PS: Si c'est intéressant, je peux vous parler dans les articles suivants des fonctionnalités de la syntaxe, de l'IDE, avec l'installation duquel j'ai eu des problèmes.