Cet article explique l'utilisation de la bibliothèque géométrique des fonctions WebGeometry pour construire des modèles de polyèdres complexes. La bibliothèque est écrite en Javascript.
Un lien vers GitHub avec un exemple qui fournit un exemple simple d'utilisation de la bibliothèque. Les commentaires et critiques sont les bienvenus.
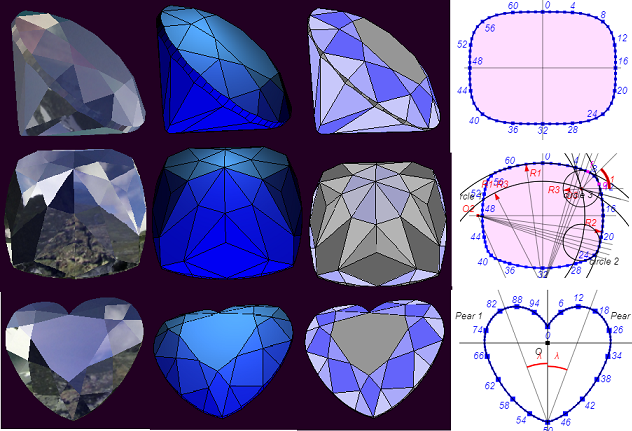
La bibliothèque ThreeJS est utilisée pour afficher les modèles précalculés à l'aide des fonctions de la bibliothèque WebGeometry. Le canevas HTML5 est utilisé pour afficher des éléments de modèle plat individuels et afficher les informations de prise en charge.
La technologie WebGL et les bibliothèques créées sur sa base, telles que ThreeJS et BadylonJS, sont utilisées sur Internet pour implémenter une variété d'objectifs liés aux graphiques 3D. Mais en gros, ils sont utilisés pour afficher des modèles tridimensionnels prêts à l'emploi dans un navigateur (précédemment créés, par exemple, dans les programmes
3ds Max ou
Blender ). Si nous sommes confrontés à la tâche de créer un modèle paramétrique, c'est-à-dire un modèle pour lequel, dans le processus d'affichage d'un objet fini dans le navigateur, nous pouvons changer ses éléments individuels en définissant les paramètres de modèle appropriés (par exemple, augmenter l'angle d'une certaine face), nous devons avoir un ensemble de fonctions géométriques qui vous permettront de créer un modèle afin qu'à l'avenir il y ait la possibilité de faire varier de manière interactive la forme des éléments individuels du modèle ou du modèle entier. Pour résoudre ce problème, nous avons besoin d'un ensemble de fonctions en langage Javascript qui implémenteront les méthodes utilisées en géométrie analytique. La bibliothèque doit avoir des fonctions pour créer des lignes, des plans et des cercles, trouver des points (ou des lignes) de leur intersection, créer des plans inclinés, et bien plus encore. Les bibliothèques ThreeJS et BadylonJS possèdent certaines de ces fonctionnalités, mais le nombre d'actions effectuées avec celles-ci ne vous permettra pas de terminer toutes les tâches qui surviennent lors de la construction d'un modèle paramétrique. Il existe plusieurs bibliothèques Javascript purement mathématiques. Parmi ceux-ci,
glMatrix et
Sylvester sont les plus largement utilisés. La bibliothèque
glMatrix est principalement destinée à travailler avec des vecteurs, des matrices et des quaternions, mais il n'y a pas de fonctions pour travailler avec des lignes et des plans. La bibliothèque
Sylvester a ces fonctions, mais elles sont présentes en quantité plutôt limitée. Cependant, il existe plusieurs livres qui décrivent la mise en œuvre de méthodes de géométrie analytique en C / C ++. Les programmes C / C ++ correspondants peuvent être utilisés comme prototypes pour créer une bibliothèque mathématique en Javascript. Par conséquent, lorsque j'ai décidé de créer des modèles paramétriques tridimensionnels de tailles de diamant pour les afficher dans un navigateur, la bibliothèque ThreeJS a été choisie par moi uniquement pour afficher les modèles déjà calculés - elle n'a pas été utilisée pour calculer la forme des modèles. Pour le calcul du formulaire lui-même, la bibliothèque WebGeometry a été créée. Cette bibliothèque était basée sur les fonctions géométriques précédemment utilisées en C / C ++, que j'ai traduites en langage Javascript. Considérons les étapes de construction d'un modèle pyramidal (taille de diamant de type Pyramide).
À la
première étape, nous devons dessiner la vue voulue du modèle, puis numéroter ses sommets. La figure ci-dessous montre la numérotation des sommets et les noms des éléments coupés inclus dans le modèle de coupe pyramidale.

Après cela, il est nécessaire de former des faces à partir des sommets numérotés. Par exemple, pour la face du site et les faces de la couronne, écrivez la séquence de sommets suivante (le premier sommet dupliqué de la face signale que la face est terminée):
0, 3, 2, 1, 0;
Les visages doivent être dans le sens antihoraire. Le fichier pyramid_index.js contient le code source pour parcourir toutes les faces de la pyramide et des commentaires détaillés. Le résultat de l'analyse est écrit dans le tableau index_cut.
Dans la
deuxième étape, nous pouvons colorer les faces du modèle. Cette étape est facultative si nous n'avons pas besoin de coloration. Supposons que nous voulons coloriser un modèle de pyramide comme suit:
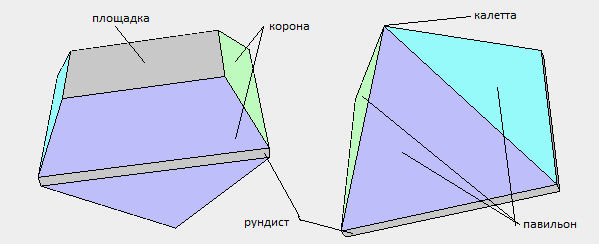
À cet effet, le fichier pyramid_colors.js est créé dans lequel se trouve la fonction facet_colors (), qui écrit les couleurs de toutes les faces dans le tableau de couleurs.
À la
troisième étape , une fois tous les sommets numérotés et les séquences de parcours de tous les sommets des faces enregistrées, il est nécessaire de définir les paramètres du modèle puis de calculer les coordonnées de tous ses sommets. Bien sûr, nous supposons que nous avons déjà décrit l'algorithme de construction pour nous-mêmes et compris comment toutes les faces du modèle seront situées dans l'espace. Pour la pyramide, nous choisirons les paramètres suivants, qui détermineront les tailles à la fois de ses parties individuelles et de l'ensemble du modèle dans son ensemble:
var DEGREE = 0.01745329251994;
Le choix des paramètres est déterminé par le développeur du modèle. Par exemple, au lieu de définir deux paramètres pour deux angles d'inclinaison de la couronne, vous pouvez spécifier un seul paramètre pour deux angles à la fois - alors ces angles seront toujours les mêmes. Vous pouvez entrer un paramètre qui détermine la taille du site. Dans ce cas, il faut soit ne pas régler la hauteur de la couronne, soit ne pas régler l'inclinaison de ses faces. Une autre option pour choisir les paramètres consiste à rendre certains paramètres calculables. Dans ce cas, lors de la modification de certains paramètres, d'autres peuvent changer leur valeur initiale. Par exemple, si nous supposons que pour la pyramide, nous avons défini un paramètre pour définir l'angle d'inclinaison des faces coronales, un autre paramètre pour la hauteur de la couronne et un autre paramètre qui définira la taille de la zone, puis lors du changement de l'angle des faces, nous serons obligés de modifier la taille de la zone ou hauteur de la couronne. D'un autre côté, si vous modifiez le paramètre qui définit la taille du pad, la valeur du paramètre qui définit la hauteur ou la pente des faces coronales changera automatiquement. L'option associée à l'application des paramètres calculés dans ce programme, ainsi que dans la construction des autres modèles de coupe présentés sur le site, n'est pas utilisée.
À la
quatrième étape , les coordonnées des sommets du modèle sont calculées. Les données initiales pour le calcul sont les valeurs des paramètres du modèle et comment nous imaginons son apparence. Le fichier pyramid_verts.js contient le texte source (avec des commentaires détaillés) de la fonction de calcul des sommets du modèle, appelée VerticesCalculation. C'est avec ce calcul que les fonctions de la bibliothèque WebGeometry sont utilisées dans cette fonction. Les résultats du calcul des coordonnées des sommets sont entrés dans le tableau des sommets. Notez que dans le programme de recherche des coordonnées des sommets, des séquences de nombres distinctes sont utilisées pour les sommets qui composent la couronne (quatre sommets), les sommets qui composent la ceinture (quatre sommets) et les sommets qui composent le pavillon (dans le modèle pyramidal, seul le sommet est inclus dans le pavillon). Ce choix de numérotation supplémentaire des sommets est utilisé pour faciliter l'orientation par le programmeur parmi les sommets coupés, car le nombre de sommets dépasse très souvent 100.
À la
cinquième étape, une fois le calcul des coordonnées des sommets terminé, il est nécessaire de construire par programmation le polyèdre (polyèdre) du modèle. Les données initiales pour sa construction sont des tableaux précédemment créés d'index_cut, de couleurs et de sommets. Un modèle de polyèdre peut être représenté simplement comme un ensemble de faces qui délimitent un polyèdre dans l'espace. La fonction CreatePolyhedron se trouve dans le fichier polyhedron.js. À la suite du travail de cette fonction, un tableau de polygones (polygones) est créé, dont le modèle tridimensionnel se compose. Chaque polygone est décrit par la fonction suivante (en fait, c'est une fonction constructeur appelée par le nouvel opérateur lors de la création d'un nouveau polygone):
function Polygon() { this.IndexFacet = [];
Étant donné que WebGL et la bibliothèque ThreeJS ont créé sur sa base un travail avec des primitives triangulaires, il est triangulé pour chaque face du modèle. On suppose que toutes les faces du modèle sont des polygones convexes. En fin de compte, la fonction CreatePolyhedron prend toutes les mesures nécessaires pour créer des structures de données qui décrivent pleinement toutes les faces du polyèdre de manière à ce qu'elles puissent être transmises aux fonctions de la bibliothèque ThreeJS pour afficher le modèle à l'écran.
À la
sixième étape , le modèle est affiché à l'écran à l'aide des fonctions ThreeJS. De manière standard, la scène, le rendu et la caméra sont créés. Afin d'examiner le modèle de coupe de tous les côtés, le programme Pyramid utilise l'élément orbitControls. Lors de la création d'autres modèles de coupe, afin d'inspecter les coupes de tous les côtés, je n'ai pas utilisé orbitControls, mais j'ai introduit la possibilité de faire pivoter le modèle lui-même. Ensuite, nous créons les mailles du modèle. Vous pouvez faire deux choses.
Dans la première méthode, nous considérons le modèle de coupe comme un ensemble de maillages de face séparés. Dans ce cas, chaque face est un objet 3D distinct. Avec cette représentation du modèle, le processus de sélection d'une face individuelle à l'aide de l'élément Three.JS, qui porte le nom de raycaster, est assez simple. De plus, cette méthode peut être complétée par la création de mailles de segments bordant chaque face.
Dans la deuxième manière, nous considérons le modèle coupé comme un objet unique, représenté par un seul maillage qui inclut immédiatement toutes les faces du modèle. Cette méthode est pratique à utiliser lors de l'affichage d'un modèle à l'aide de shaders. Cette méthode n'est pas utilisée dans le modèle de coupe Pyramid, mais elle est utilisée pour créer des modèles de coupe Octagon, Brilliant et autres qui peuvent être vus sur mon site Web.
À la
septième étape , les boutons et fonctions qui leur sont associés sont créés pour vous permettre de modifier la valeur des paramètres qui déterminent la forme et la taille du modèle. Lorsqu'une touche est enfoncée, une fonction est appelée qui augmente ou diminue la valeur du paramètre correspondant. Cela signifie qu'il est nécessaire de recalculer la valeur des coordonnées des sommets du modèle. Après le recomptage, l'exactitude du modèle nouvellement construit est vérifiée. Par exemple, il est déterminé si certaines valeurs sont hors tolérance. Dans le cas des modèles taillés au diamant, cela revient généralement à vérifier si la coupe convexe subsiste après sa reconstruction. La vérification du renflement est la suivante. À travers chaque face, un plan est dessiné dans lequel se trouve cette face, puis la position de chaque sommet du modèle par rapport à ce plan est déterminée. Tous les sommets doivent être situés du même côté de ce plan. Si le modèle est considéré comme incorrect, le paramètre retrouve sa valeur d'origine et le modèle est à nouveau reconstruit. Pour les modèles coupés ayant une ceinture non convexe (seul cet élément de certaines coupes, comme le cœur, peut être non convexe), la convexité est vérifiée séparément pour la couronne et séparément pour le pavillon. Le rundist, cependant, est exclu du chèque. Pour les modèles simples, vous pouvez vous limiter à une simple vérification des paramètres. Par exemple, si nous construisons un modèle de maison, le toit ne doit pas être supérieur à une certaine hauteur à l'avance. Par conséquent, en réglant simplement la restriction de ce paramètre en amplitude, nous obtenons le résultat souhaité. Une fois les boutons de paramètres ajoutés, il est très souhaitable d'afficher visuellement la valeur de chaque paramètre lorsqu'il change après avoir cliqué sur le bouton. Pour ce faire, un canevas bidimensionnel HTML5 est créé et à côté du bouton correspondant la valeur du paramètre s'affiche dessus.
Ainsi, nous avons examiné toutes les étapes de la construction d'un modèle en utilisant l'exemple Pyramid. Pour la pyramide (ainsi que pour tous les autres modèles du site), j'ai créé un autre programme Pyramid_text.html. L'exemple de ce programme montre comment afficher du texte en trois dimensions pour numéroter les sommets d'un modèle. Si quelqu'un veut savoir comment les modèles complexes sont construits, alors vous devriez envisager de construire des modèles
(voir GitHub) dans l'ordre suivant:
Octogone . Un modèle qui illustre la création d'avions de différentes manières et le travail avec ces avions. Lors de la construction d'un modèle, les méthodes utilisées lors de l'utilisation de vecteurs et de lignes dans l'espace sont également utilisées.
Brillant . Il s'agit de la taille de diamant classique et la plus courante. Certains éléments de la construction d'un modèle tridimensionnel de cette coupe seront utilisés à l'avenir lors de la création des facettes MoonMarquise, MoonPear et Heart. Le calcul de la ceinture de cette coupe, qui a la forme d'une superellipse, est indiqué séparément dans le programme BrilliantGirdlt.html. Dans ce programme, la ligne de ceinture est construite sur une toile bidimensionnelle (toile).
MoonMarquise . La taille marquise, comme Brilliant, est l'une des tailles de diamant classiques. Contrairement à une simple facette de ce type (Marquise), les soi-disant «facettes de la lune» sont ajoutées à la facette MoonMarquise du pavillon. Le cutter MoonMarquise est formé de deux arcs d'ellipses. Une construction détaillée de cette ceinture sur toile est présentée dans le programme MarquiseGirdle.html. Le texte de ce programme contient des commentaires détaillés sur la construction. Nous notons un point concernant le calcul de la ligne de ceinture - il utilise la propriété d'une tangente à une ellipse. Il est considéré, par exemple, dans le livre "Course of Analytical Geometry" (l'auteur de ce livre est N.I. Muskhelishvili).
MoonPear Le mérou coupé MoonPear est formé par les arcs de trois ellipses. Sa construction est basée sur la construction de la ceinture coupée Marquise, mais est plus complexe. Pour voir la ligne de ceinture Marquise et comment diviser le gundist en segments, exécutez le programme PearGirdle.html.
Coeur La coupe «cœur» est l'une des coupes classiques, mais elle a, contrairement à la plupart des types de coupes, une forme de ceinture non convexe. Le rudiste coupe cœur est composé de deux gaines coupées poire inclinées l'une par rapport à l'autre. Sur le canevas, vous pouvez voir la ligne de ceinture en exécutant le programme HeartGirdle.html. Construire une coupe de cœur est tout un défi.
Croix de Malte . Le cutter de la coupe «Croix de Malte» est réalisé sous la forme d'un «coussin» (coussin). Les boutures avec une telle ceinture se sont récemment généralisées. La ligne de cette ceinture est constituée de huit arcs conjugués de cercles - quatre arcs principaux bordant l'oreiller sur quatre côtés et quatre arcs de plus petite taille associant les arcs principaux de l'oreiller aux coins de la ceinture. En exécutant les programmes CushionGirdle_1.html et CushionGirdle_2.html, vous pouvez voir la forme de la ligne de la ceinture, le travail de tous les paramètres définissant sa forme et la division de la ceinture en segments.
Étoile pentagonale . Le coupe-étoile pentagonal est formé par une ligne portant le nom de l'épitrochoïde. L'épitrochoïde est une courbe liée à la cycloïde. Dans le programme Wavy_Pentagon_Girdle.html, en changeant les valeurs des paramètres, vous pouvez changer l '«ondulation» de la ceinture et même changer le pentagone en un polygone avec un nombre différent de protubérances («pétales»). Cependant, il faut se rappeler que le modèle de cette coupe lui-même est construit pour la valeur du paramètre «Nombre de pétales» égal à 5.
Comme mentionné précédemment, pour tous les modèles ci-dessus, des programmes sont créés affichant le nombre de sommets coupés. Dans ces programmes, un basculement est effectué entre l'affichage direct de tous les sommets du modèle et l'indication des nombres de sommets pour la couronne, la ceinture et le pavillon séparément. Supposons que dans le modèle de coupe maltais, vous souhaitez créer un plan passant par les sommets avec les numéros 84, 88 et 145. Au lieu d'utiliser ces numéros pour identifier les points par lesquels le plan passe lors de la création d'un plan à l'aide de la fonction CreatePlaneThreePoints, un enregistrement utilisant un autre numérotation des pics de la ceinture et du pavillon:
var plane = new Plane3D(); plane.CreatePlaneThreePoints(girdle[68], girdle[72], crown[1]);
Il convient de noter que les programmes affichant les nombres de sommets du modèle fonctionnent très lentement (au moins sur mon ordinateur). Cela peut prendre plusieurs secondes avant que la sortie des numéros de sommets du modèle soit terminée.
Pour résumer tout ce qui précède, à mon avis, le choix des polyèdres (modèles coupés) pour démontrer le fonctionnement des fonctions géométriques est l'une des meilleures options. Après avoir examiné le travail des exemples ci-dessus, nous pouvons procéder à la création d'objets géométriques liés à des domaines d'activité complètement différents de la modélisation de la taille du diamant.