Solution numérique de modèles mathématiques d'objets donnés par des systèmes d'équations différentielles

Présentation:

Dans la modélisation mathématique d'un certain nombre de dispositifs techniques, des systèmes d'équations non linéaires différentielles sont utilisés. De tels modèles sont utilisés non seulement en technologie, ils sont utilisés en économie, chimie, biologie, médecine et gestion.

L'étude du fonctionnement de tels appareils nécessite la solution de ces systèmes d'équations. Étant donné que la majeure partie de ces équations sont non linéaires et non stationnaires, il est souvent impossible d'obtenir leur solution analytique.

Il est nécessaire d'utiliser des méthodes numériques, dont la plus connue est la méthode Runge-Kutta [1]. Quant à Python, dans les publications sur les méthodes numériques, par exemple [2,3], il y a très peu de données sur l'utilisation de Runge - Kutta, et il n'y a pas de données sur sa modification à la méthode Runge - Kutta - Felberg.

Actuellement, grâce à son interface simple, la fonction odeint du module scipy.integrate a la plus grande distribution en Python. La deuxième ode de fonction de ce module implémente plusieurs méthodes, y compris la méthode Runge-Kutta-Felberg à cinq rangs mentionnée, mais, en raison de son universalité, ses performances sont limitées.

Le but de cette publication est une analyse comparative des moyens énumérés pour résoudre numériquement des systèmes d'équations différentielles avec un auteur modifié sous Python en utilisant la méthode Runge-Kutta-Felberg. La publication fournit également des solutions aux problèmes de valeurs limites pour les systèmes d'équations différentielles (SDE).

Brèves données théoriques et réelles sur les méthodes et les logiciels envisagés pour la solution numérique de CDS

Le problème de Cauchy

Pour une équation différentielle du nième ordre, le problème de Cauchy consiste à trouver une fonction satisfaisant l'égalité:



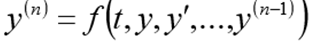
et conditions initiales



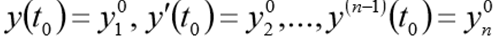
Avant de résoudre ce problème doit être réécrit sous la forme du CDS suivant

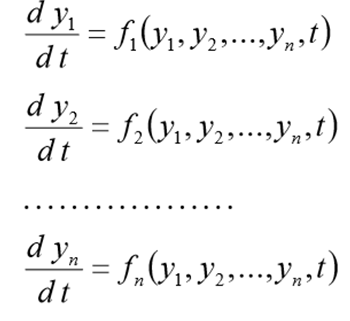
(1)

avec conditions initiales



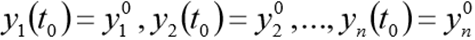Module Scipy.integrate

Le module a deux fonctions ode () et odeint (), conçues pour résoudre des systèmes d'équations différentielles ordinaires (ODE) du premier ordre avec des conditions initiales en un point (problème de Cauchy). La fonction ode () est plus universelle et la fonction odeint () (intégrateur ODE) a une interface plus simple et résout bien la plupart des problèmes.

Fonction Odeint ()

La fonction odeint () a trois arguments requis et de nombreuses options. Il a le format suivant odeint (func, y0, t [, args = (), ...]) L'argument func est le nom Python de la fonction de deux variables, dont la première est la liste y = [y1, y2, ..., yn ], et le second est le nom de la variable indépendante.

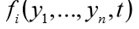
La fonction func doit renvoyer une liste de n valeurs de fonction pour une valeur donnée de l'argument indépendant t. En fait, la fonction func (y, t) implémente le calcul des côtés droits du système (1).

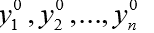
Le deuxième argument y0 de odeint () est un tableau (ou une liste) de valeurs initiales à t = t0.

Le troisième argument est un tableau de points de temps auquel vous souhaitez obtenir une solution au problème. Dans ce cas, le premier élément de ce tableau est considéré comme t0.

La fonction odeint () renvoie un tableau de taille len (t) x len (y0). La fonction odeint () possède de nombreuses options qui contrôlent son fonctionnement. Les options rtol (erreur relative) et atol (erreur absolue) déterminent l'erreur de calcul ei pour chaque valeur de yi selon la formule



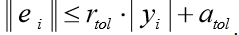
Ils peuvent être des vecteurs ou des scalaires. Par défaut



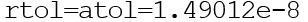Fonction Ode ()

La deuxième fonction du module scipy.integrate, qui est conçue pour résoudre des équations et des systèmes différentiels, est appelée ode (). Il crée un objet ODE (type scipy.integrate._ode.ode). Ayant un lien vers un tel objet, il faut utiliser ses méthodes pour résoudre des équations différentielles. De même que la fonction odeint (), la fonction ode (func) consiste à réduire le problème à un système d'équations différentielles de la forme (1) et à utiliser sa fonction des côtés droit.

La seule différence est que la fonction du côté droit func (t, y) accepte une variable indépendante comme premier argument, et la liste des valeurs des fonctions désirées comme deuxième. Par exemple, la séquence d'instructions suivante crée un ODE qui représente une tâche Cauchy.

Runge - Méthode Kutta

Lors de la construction d'algorithmes numériques, nous supposons qu'une solution à ce problème différentiel existe, elle est unique et possède les propriétés de lissage nécessaires.

Dans la solution numérique du problème de Cauchy

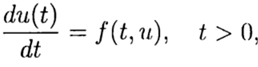
(2)

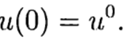
(3)

selon la solution connue au point t = 0, il faut trouver une solution de l'équation (3) pour les autres t. Dans la solution numérique du problème (2), (3), nous utiliserons une grille uniforme, pour simplifier, dans la variable t avec un pas t> 0.

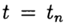
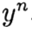
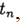
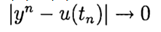
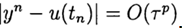
Une solution approximative au problème (2), (3) au point dénoter . La méthode converge en un point si à . La méthode a un pième ordre de précision si , p> 0 pour . Le schéma de différence le plus simple pour une solution approximative au problème (2), (3) est

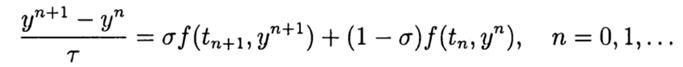
(4)

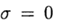
À nous avons une méthode explicite et dans ce cas, le schéma de différence se rapproche de l'équation (2) avec le premier ordre. Conception symétrique en (4) a un second ordre d'approximation. Ce schéma appartient à la classe des implicites - pour déterminer la solution approximative sur une nouvelle couche, il est nécessaire de résoudre le problème non linéaire.

Il est pratique de construire des schémas d'approximation explicites de second ordre et d'ordre supérieur basés sur la méthode prédicteur-correcteur. Au stade du prédicteur (prédiction), un schéma explicite est utilisé.

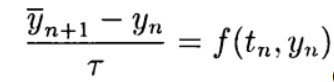
(5)

et au stade du correcteur (raffinement), un diagramme



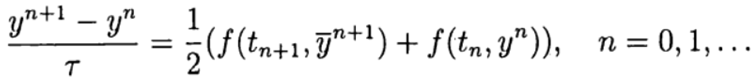
Dans les méthodes Runge - Kutta en une étape, les idées du correcteur-prédicteur sont pleinement réalisées. Cette méthode est écrite sous forme générale:

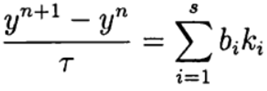
(6)

où



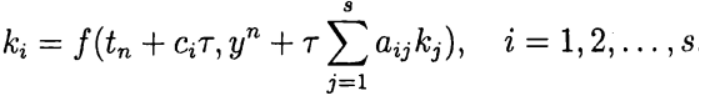
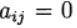
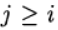
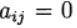
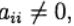
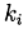
La formule (6) est basée sur s calculs de la fonction f et est appelée étape s. Si à nous avons la méthode explicite Runge - Kutta. Si pour j> 1 et alors déterminé implicitement à partir de l'équation:

(7)

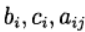
Cette méthode Runge-Kutta est considérée comme implicitement diagonale. Paramètres déterminer une variante de la méthode Runge - Kutta. La représentation suivante de la méthode est utilisée (table de boucher)



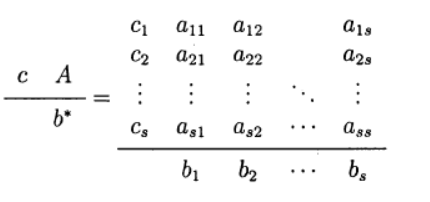
L'une des plus courantes est la méthode Runge - Kutta explicite du quatrième ordre.

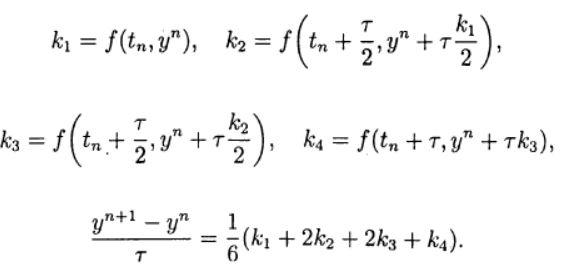
(8)

Runge - Kutta - Méthode Felberg

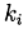
Je donne la valeur des coefficients calculés méthode

(9)

Au vu de (9), la solution générale a la forme:

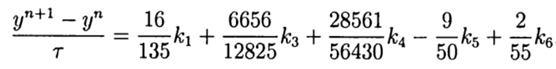
(10)

Cette solution offre le cinquième ordre de précision, il reste à l'adapter à Python.

Expérience de calcul pour déterminer l'erreur absolue de la solution numérique d'une équation différentielle non linéaire 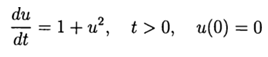utilisant les deux fonctions def odein (), def oden () du module scipy.integrate et les méthodes Runge - Kutta et Runge - Kutta - Felberg adaptées à Python

Nous obtenons:









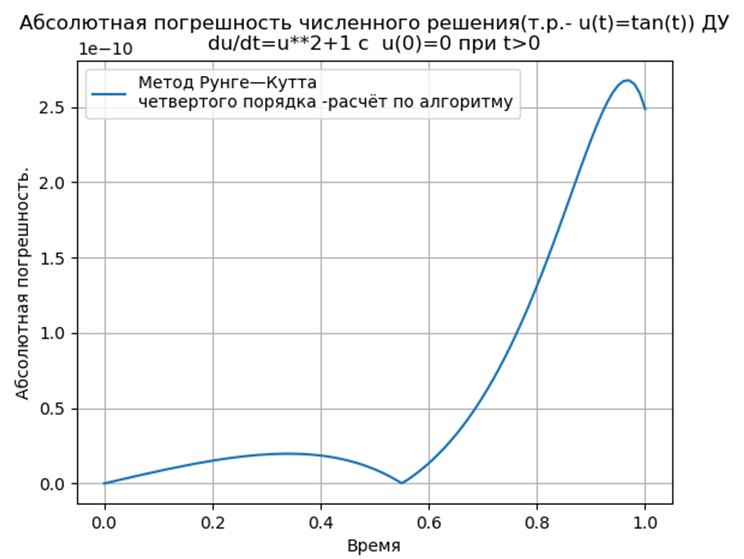
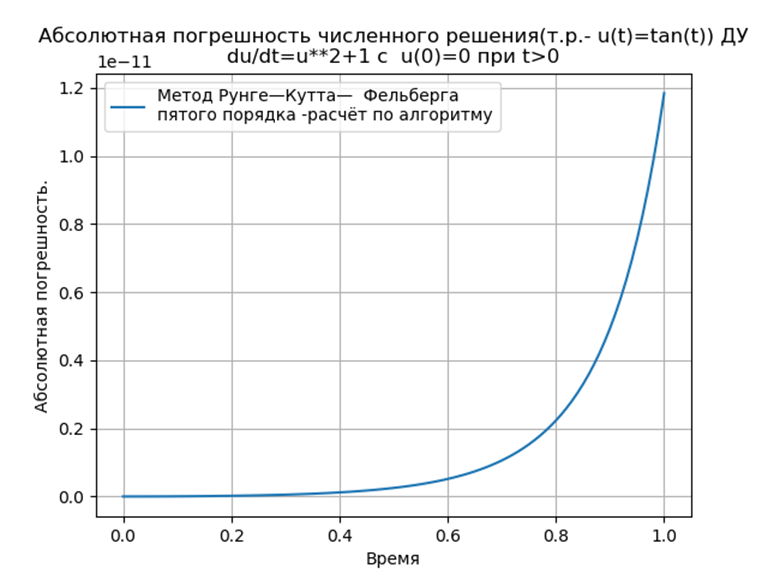
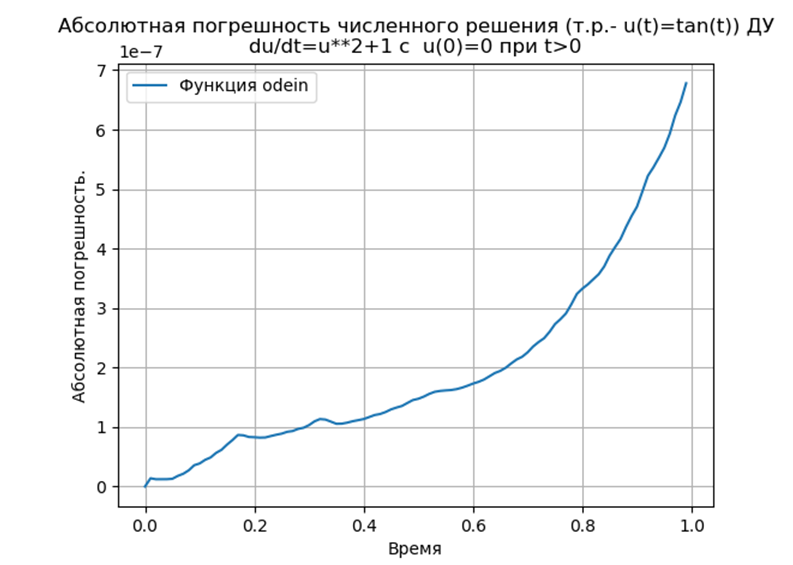
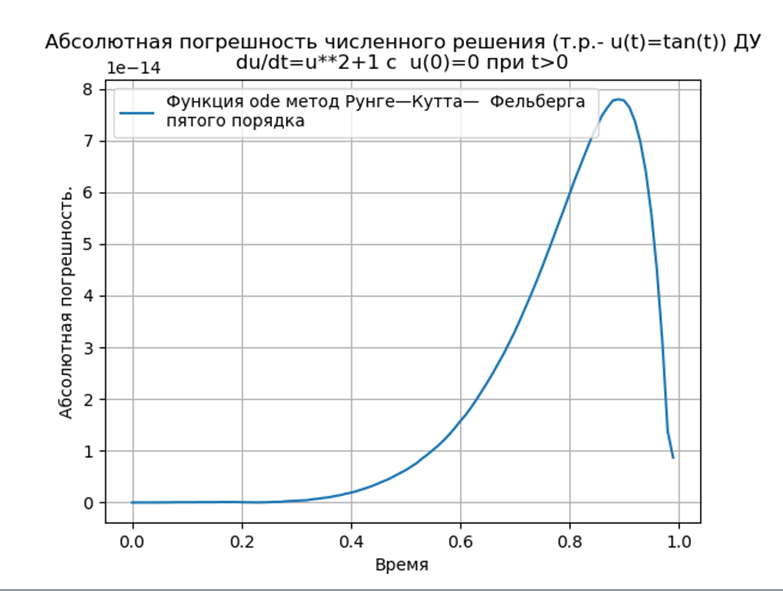Conclusion:

Les méthodes Runge - Kutta et Runge - Kutta - Felberg adaptées à Python ont un absolu inférieur à une solution utilisant la fonction odeint, mais plus qu'une solution utilisant la fonction edu. Il est nécessaire de mener une étude de performance.

Une expérience numérique comparant la vitesse de la solution numérique du SDE lors de l'utilisation de la fonction ode avec l'attribut dopri5 (méthode Runge - Kutta du 5ème ordre) et en utilisant la méthode Runge - Kutta - Felberg adaptée à Python

Une analyse comparative est réalisée en utilisant le problème du modèle donné dans [2] comme exemple. Afin de ne pas répéter la source, je présenterai la formulation et la solution du problème du modèle à partir de [2].

Résolvons le problème de Cauchy, qui décrit le mouvement d'un corps projeté avec une vitesse initiale v0 à un angle α par rapport à l'horizon en supposant que la résistance de l'air est proportionnelle au carré de la vitesse. Sous forme vectorielle, l'équation du mouvement a la forme



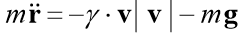
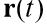
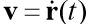
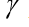
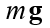
où Est le rayon du vecteur du corps en mouvement, Est le vecteur vitesse du corps, - coefficient de traînée, vecteur forces du poids corporel de la masse m, g - accélération de la gravité.



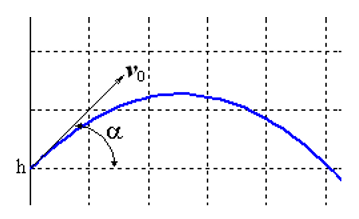
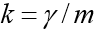
La particularité de cette tâche est que le mouvement se termine à un moment inconnu dans le temps lorsque le corps tombe au sol. Si désigné , puis sous forme de coordonnées, nous avons un système d'équations:



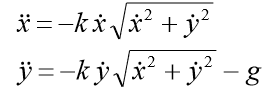
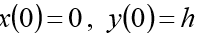
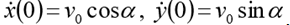
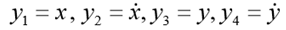
Les conditions initiales doivent être ajoutées au système: (h hauteur initiale) . Mettez . Ensuite, le système ODE de premier ordre correspondant prend la forme:



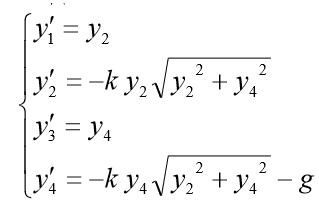
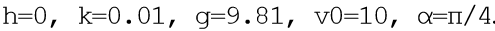
Pour le problème du modèle, nous mettons . En omettant une description assez détaillée du programme, je ne donnerai qu'une liste des commentaires auxquels, je pense, le principe de son fonctionnement sera clair. Le programme a ajouté un compte à rebours pour l'analyse comparative.



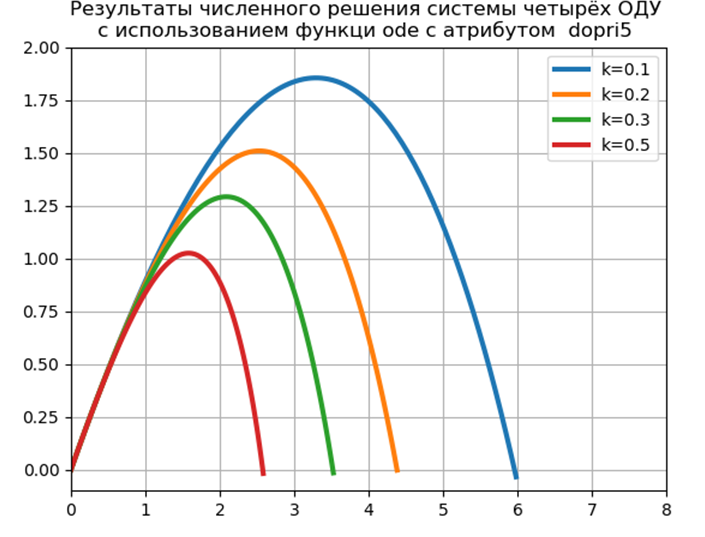
Nous obtenons:

Temps de vol = 1,2316 Distance = 5,9829 Hauteur = 1,8542
Temps de vol = 1,1016 Distance = 4,3830 Hauteur = 1,5088
Temps de vol = 1,0197 Distance = 3,5265 Hauteur = 1,2912
Temps de vol = 0,9068 Distance = 2,5842 Hauteur = 1,0240
Temps pour le problème du modèle: 0.454787



Pour implémenter une solution numérique du CDS en utilisant des outils Python sans utiliser de modules spéciaux, j'ai proposé et étudié la fonction suivante:

def increment(f, t, y, tau
k1=tau*f(t,y)
k2=tau*f(t+(1/4)*tau,y+(1/4)*k1)
k3 =tau *f(t+(3/8)*tau,y+(3/32)*k1+(9/32)*k2)
k4=tau*f(t+(12/13)*tau,y+(1932/2197)*k1-(7200/2197)*k2+(7296/2197)*k3)
k5=tau*f(t+tau,y+(439/216)*k1-8*k2+(3680/513)*k3 -(845/4104)*k4)
k6=tau*f(t+(1/2)*tau,y-(8/27)*k1+2*k2-(3544/2565)*k3 +(1859/4104)*k4-(11/40)*k5)
return (16/135)*k1+(6656/12825)*k3+(28561/56430)*k4-(9/50)*k5+(2/55)*k6

La fonction d'incrémentation (f, t, y, tau) fournit le cinquième ordre de la méthode de résolution numérique. D'autres fonctionnalités du programme peuvent être trouvées dans la liste suivante:


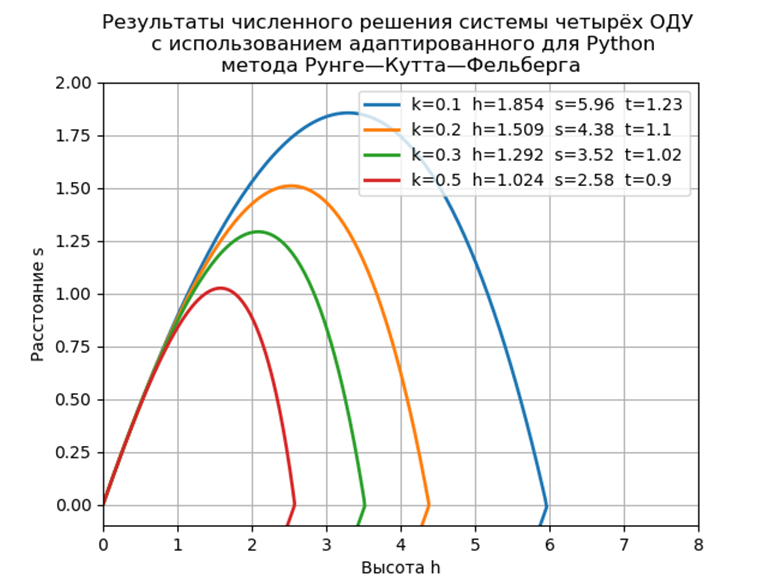
Nous obtenons:

Temps pour le problème du modèle: 0,259927



Conclusion

L'implémentation logicielle proposée du problème de modèle sans l'utilisation de modules spéciaux a des performances presque deux fois plus rapides qu'avec la fonction ode, mais il ne faut pas oublier que l'ode a une plus grande précision de la solution numérique et la possibilité de choisir une méthode de solution.

Résolution d'un problème de valeur limite avec des conditions aux limites séparées par les threads

Nous donnons un exemple d'un problème de valeur limite spécifique avec des conditions aux limites séparées par des threads:

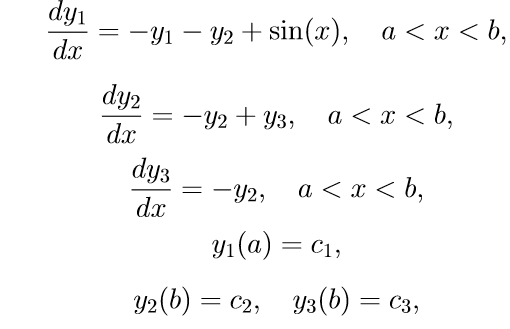
(11)

Pour résoudre le problème (11), nous utilisons l'algorithme suivant:

1. Nous résolvons les trois premières équations inhomogènes du système (11) avec les conditions initiales

Nous introduisons la notation pour résoudre le problème de Cauchy:


2. Nous résolvons les trois premières équations homogènes du système (11) avec les conditions initiales

Nous introduisons la notation pour résoudre le problème de Cauchy:


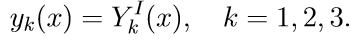
3. Nous résolvons les trois premières équations homogènes du système (11) avec les conditions initiales



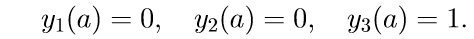
Nous introduisons la notation pour résoudre le problème de Cauchy:



4. La solution générale du problème aux valeurs limites (11) en utilisant les solutions des problèmes de Cauchy s'écrit comme une combinaison linéaire de solutions:

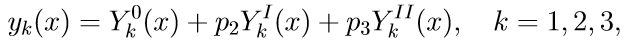
où p2, p3 sont des paramètres inconnus.

5. Pour déterminer les paramètres p2, p3, nous utilisons les conditions aux limites des deux dernières équations (11), c'est-à-dire les conditions pour x = b. En substituant, nous obtenons un système d'équations linéaires par rapport aux p2, p3 inconnus:
(12)
En résolvant (12), on obtient les relations pour p2, p3.

En utilisant l'algorithme ci-dessus en utilisant la méthode Runge - Kutta - Felberg, nous obtenons le programme suivant:


Nous obtenons:

y0 [0] = 0,0
y1 [0] = 1,0
y2 [0] = 0,7156448588231397
y3 [0] = 1,324566562303714
y0 [N-1] = 0,9900000000000007
y1 [N-1] = 0,1747719838716767
y2 [N-1] = 0,8
y3 [N-1] = 0,5000000000000001
Temps pour le problème du modèle: 0,070878

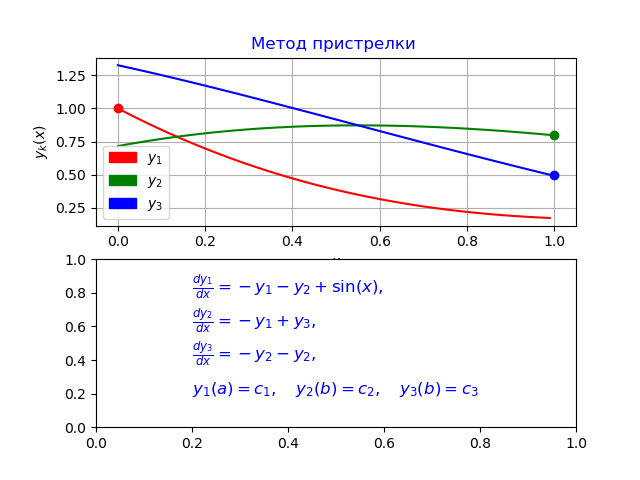
Conclusion

Le programme que j'ai développé diffère de l'erreur donnée dans [3], qui confirme l'analyse comparative de la fonction odeint donnée au début de l'article avec la méthode Runge - Kutta - Felberg implémentée en Python.

Références:

1. Solution numérique de modèles mathématiques d'objets définis par des systèmes composites d'équations différentielles.

2. Introduction au Python scientifique.

3. N.M. Polyakova, E.V. Shiryaeva Python 3. Création d'une interface utilisateur graphique (en utilisant l'exemple de résolution du problème des valeurs limites pour les équations différentielles ordinaires linéaires par la méthode de prise de vue). Rostov-sur-le-Don 2017.