Bonjour, Habr! Dans cet article, je parlerai de la création d'un modèle mathématique d'un long pipeline pour le programme CAE SimulationX dans Modelica. Il s'agira de calculer les processus ondulatoires (pulsations de pression, coup de bélier, etc.) dans une conduite hydraulique en utilisant la méthode des caractéristiques. Malgré le fait que cette méthode soit assez ancienne, RuNet ne contient pas suffisamment d'informations sur son application pour résoudre les problèmes appliqués.

Sous la coupe, j'essaierai d'expliquer pourquoi il est nécessaire de prendre en compte les processus de vagues dans les pipelines, de mettre en évidence les problèmes que j'ai rencontrés lors de la programmation et à la fin je donnerai une comparaison du processus de pulsations de pression pendant le fonctionnement d'une pompe à eau haute pression à trois plongeurs sur une simple longue canalisation dans le modèle et sur le stand URACA dans Allemagne.

Présentation

Dans la pratique de l'ingénierie, en règle générale, peu d'attention est accordée aux processus de vagues dans les pipelines. L'exemple le plus célèbre, lorsque les processus ondulatoires gâchent la vie d'un ingénieur, est un coup de bélier:



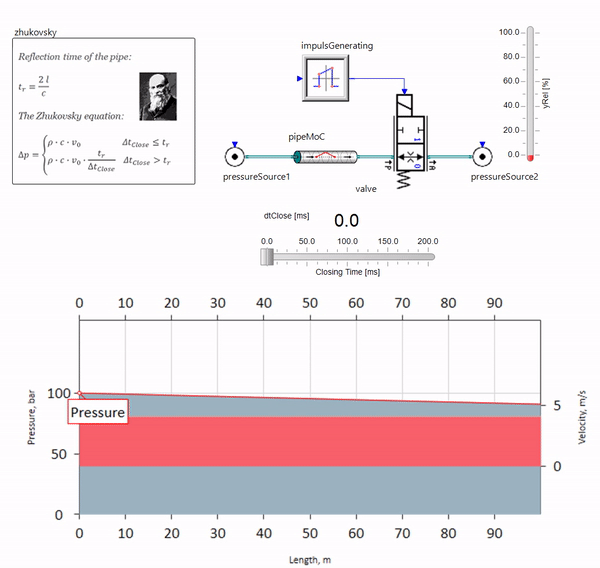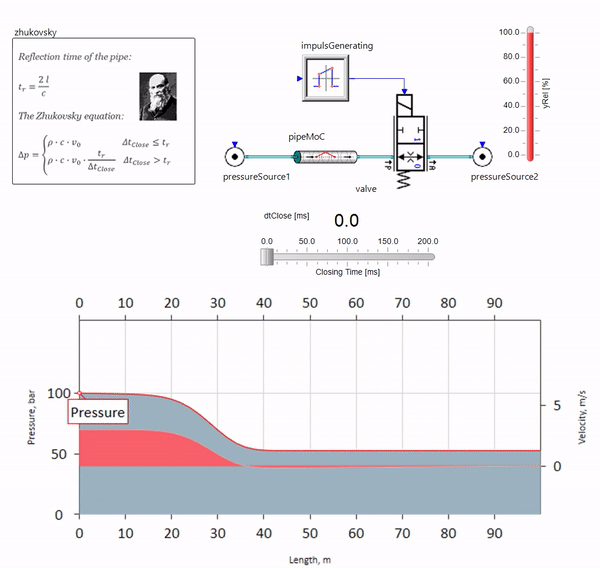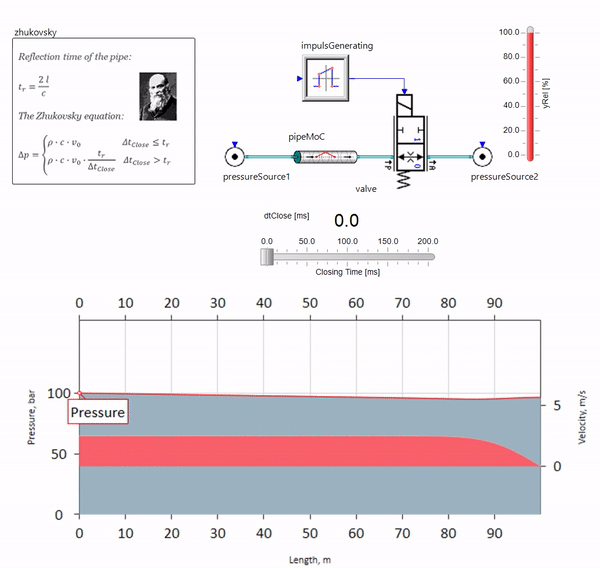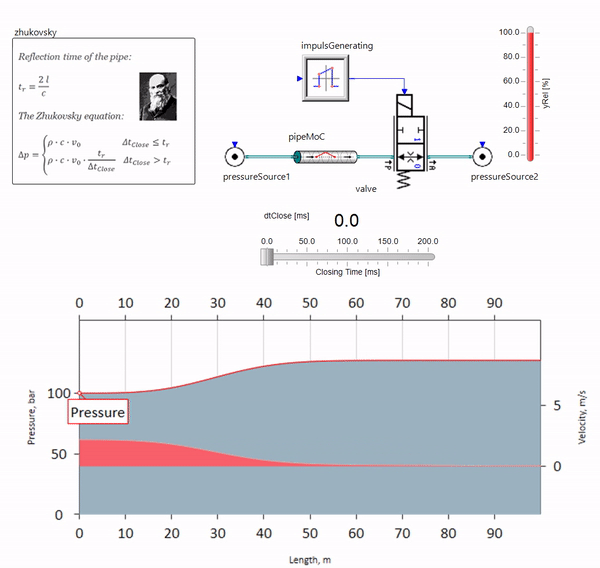
Lorsque la vanne se ferme rapidement à la fin de la canalisation, en aval, une onde de pression se produit qui se déplace en amont à la vitesse locale du son (pour l'eau, environ 1500 m / s), se réfléchit à partir d'une source de pression constante, retourne à la vanne et se reflète à partir de cette fois avec un signe négatif. Ce processus est répété jusqu'à ce que toute l'énergie soit dépensée pour le frottement, et jusque-là, la soupape et l'ensemble du pipeline sont soumis à des charges de choc, dont l'amplitude et la fréquence dépendent de la longueur du pipeline et de la vitesse initiale de l'écoulement du fluide.

L'hydroblow avec la précision nécessaire pour résoudre des problèmes pratiques a été décrit à la fin du 19ème siècle par Nikolai Zhukovsky, résolvant ainsi le problème des accidents à l'approvisionnement en eau de Moscou. Depuis lors, la formule pour calculer le saut de pression lorsque la vanne est fermée rapidement est appelée formule Zhukovsky partout dans le monde:

$$

$$\ Delta p = \ rho \ cdot c \ cdot \ Delta v$$

Le coup de bélier dans la pratique se manifeste, en règle générale, avec des longueurs de pipeline de cent mètres. Aux longueurs ci-dessous, il est déjà difficile de trouver des équipements hydrauliques qui pourraient se fermer plus rapidement que l'onde de pression transmise par la vanne et en arrière (la condition pour l'apparition de coups de bélier). Néanmoins, même des pipelines relativement courts peuvent encore ruiner la vie des ingénieurs si le système a une source de pulsations de débit (par exemple, une pompe volumétrique avec un nombre fini de plongeurs).



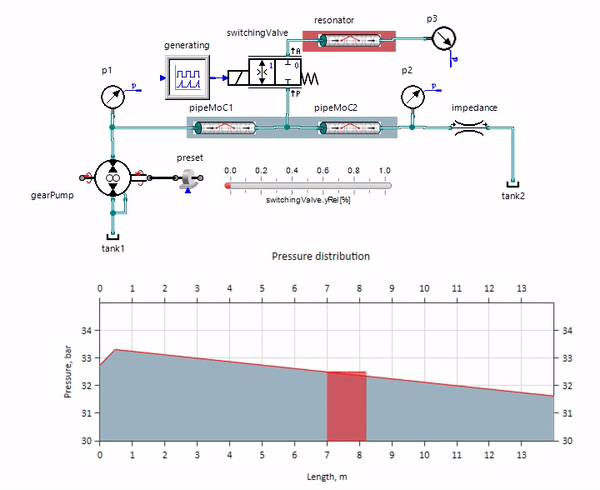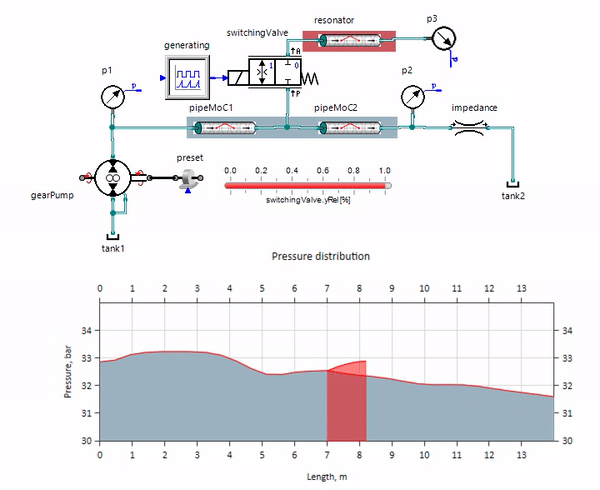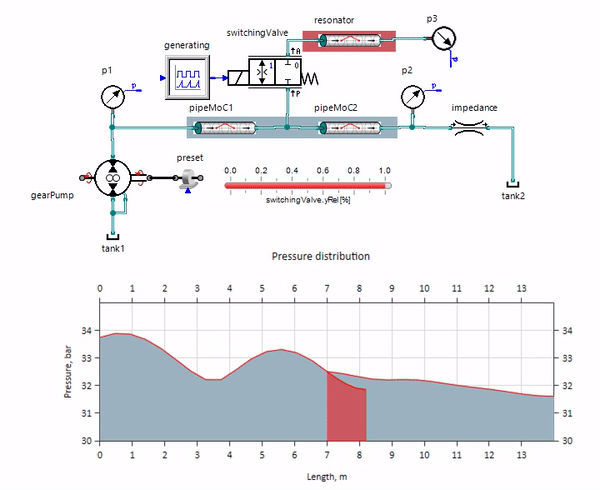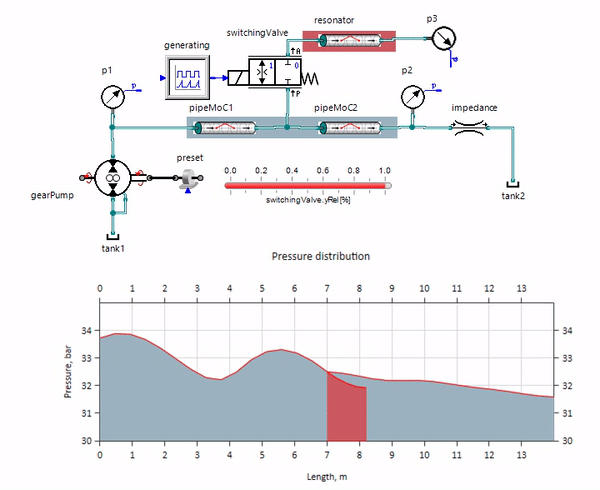
Le gif montre l'effet bénéfique d'un morceau de pipeline d'un peu plus d'un mètre de long. Sa longueur est égale à un quart de la longueur d'onde de pression, donc lorsque vous le connectez au pipeline principal, le soi-disant onde stationnaire, qui en antiphase frappe la source des pulsations et les supprime de cette façon (c'est ce qu'on appelle l'amortisseur de pulsations quart d'onde). Il est clair qu'avec une combinaison malheureuse de circonstances, l'effet peut être le contraire.

Dans ma pratique, j'ai essayé pendant longtemps d'écarter les processus ondulatoires, car leur calcul a nécessité une compréhension plus approfondie des méthodes matanes et numériques, que j'ai traitées avec négligence tout au long de mes études. Mais quand un jour j'ai vu de mes propres yeux qu'un conseil standard (mettre partout un HPP, un accumulateur hydraulique, organiser une sauvegarde à l'entrée de la pompe) n'aide pas non plus à se débarrasser des pulsations sur le banc, ni d'ailleurs à les rapprocher de la compréhension des processus, j'ai dû aller plus loin dans le tapis . Surtout à ma honte, mon directeur de recherche a déjà commencé à écrire un modèle de pipeline en C ++ pour moi.

1. Modèle unidimensionnel d'une ligne hydraulique en paramètres distribués

Le principal problème qui fait que les modèles unidimensionnels traditionnels décrits par des équations différentielles ordinaires dépassent la zone de confort est que le pipeline le plus simple, même avec les hypothèses les plus atroces (est complètement rempli de liquide, a une longueur de section constante, la vitesse du fluide est moyennée sur la section, les processus de transfert de chaleur ne sont pas considéré) est décrit par des équations différentielles dans des paramètres distribués (équations d'Euler, ne prenant en compte que la force de masse et le frottement sur le côté droit de la seconde avneniya):

$$

$$\ frac {\ partial \ rho} {\ partial t} + \ frac {\ partial (\ rho v)} {\ partial x} = 0,$$

$$

$$\ frac {\ partial (\ rho v)} {\ partial t} + \ frac {\ partial (\ rho v ^ 2 + p)} {\ partial x} = \ rho \ cdot (G + F),$$

où $$$\ rho$- densité $$$v$- vitesse $$$p$- pression $$$F$- pertes par frottement, $$$G$- chute de pression provoquée par la force gravitationnelle.

C'est-à-dire intégrez maintenant vous avez besoin non seulement de temps $$$t$mais aussi en coordonnées spatiales $$$x$.
Dans le cas des liquides, vous pouvez simplifier un peu plus votre vie en réécrivant les équations des variables conservatrices aux variables primitives (vitesse et pression):

$$

$$\ frac {\ partial p} {\ partial t} + v \ frac {\ displaystyle \ partial p} {\ displaystyle \ partial x} + \ rho \; c ^ 2 \ frac {\ partial v} {\ partial x } = 0$$

$$

$$\ frac {\ partial v} {\ partial t} + \ frac1 \ rho \ frac {\ displaystyle \ partial p} {\ displaystyle \ partial x} + v \ frac {\ displaystyle \ partial v} {\ displaystyle \ partial x} = F + G$$

où $$$c$- vitesse du son.

Maintenant, si nous acceptons que la vitesse du son est nettement supérieure à la vitesse du mouvement fluide $$$v \ ll c$(ce qui est vrai en l'absence de cavitation), les équations deviendront encore un peu plus simples:

$$

$$\ frac {\ partial p} {\ partial t} + \ rho \; c ^ 2 \ frac {\ partial v} {\ partial x} = 0$$

$$

$$\ frac {\ partial v} {\ partial t} + \ frac1 \ rho \ frac {\ displaystyle \ partial p} {\ displaystyle \ partial x} = F + G$$

Pour résoudre ces équations, d'une manière ou d'une autre, débarrassez-vous de la différenciation des coordonnées spatiales $$$x$. Cela peut être fait de front si vous remplacez le différentiel spatial par un schéma de différence finie, et dans le cas du temps, passez simplement au différentiel complet, en disant que dans la même cellule, les paramètres d'état ne dépendent pas de la coordonnée:

$$

$$\ frac {dp} {dt} = - \ rho \; c ^ 2 \ frac {\ triangle v} {\ triangle x}$$

$$

$$\ frac {dv} {dt} = F + G- \ frac1 \ rho \ frac {\ displaystyle \ triangle p} {\ displaystyle \ triangle x}$$

Maintenant, ces équations peuvent être résolues comme des équations différentielles ordinaires, divisant la longueur du tuyau en plusieurs volumes finis. Donc, cela se fait , par exemple, dans le package Simscape, dans MATLAB Simulink, et donc le problème a été résolu jusqu'à récemment dans SimulationX .
Bien sûr, quelque chose de cette façon peut être calculé, mais les fluctuations numériques qui surviennent dans ce cas sont considérablement entravées:

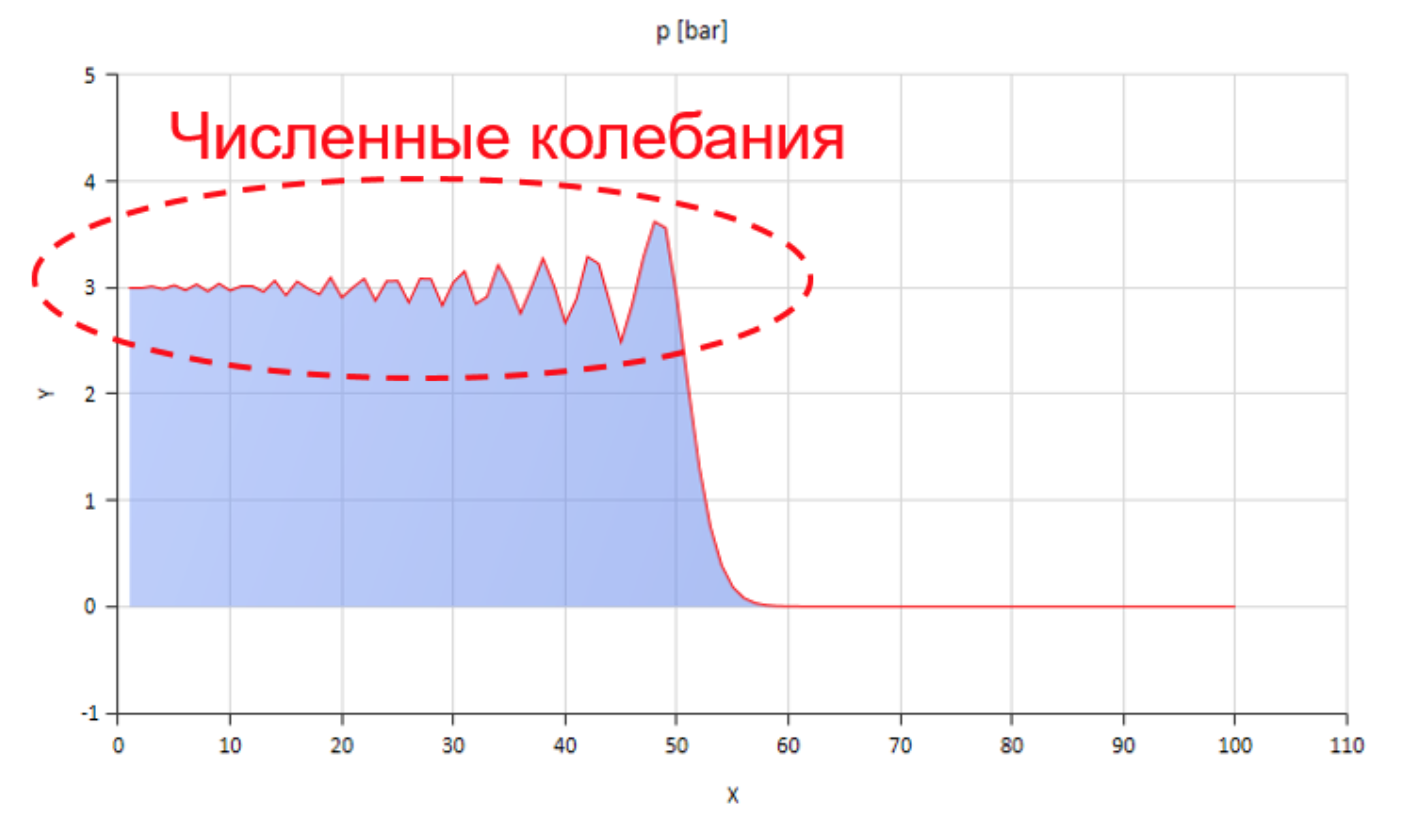La figure montre l'avant de l'onde de pression se déplaçant de gauche à droite.

Vous pouvez gérer ces oscillations, par exemple en introduisant une diffusion numérique, mais la vitesse de propagation des ondes est alors considérablement déformée. Vous pouvez augmenter le frottement (en aidant notamment à augmenter sa composante non stationnaire), mais le modèle cesse alors de refléter l'essence physique.

Il est préférable d'utiliser une méthode différente de transformation des équations des paramètres distribués en équations différentielles ordinaires, par exemple, la méthode des caractéristiques.

2. Méthode de caractérisation

Wikipedia recommande la «méthode des caractéristiques» recommande:

... pour trouver des caractéristiques le long desquelles l'équation différentielle partielle se transforme en une équation différentielle ordinaire. Dès que des équations différentielles ordinaires sont trouvées, elles peuvent être résolues le long des caractéristiques et la solution trouvée peut être transformée en une solution de l'équation différentielle partielle d'origine.

C’est comme une pierre philosophale, mais au lieu de transformer les métaux en or, nous transformons les équations différentielles partielles en équations ordinaires, et vice versa. La question se pose: «comment appliquer cela dans la pratique?», Et de préférence plus efficacement que les alchimistes médiévaux ...

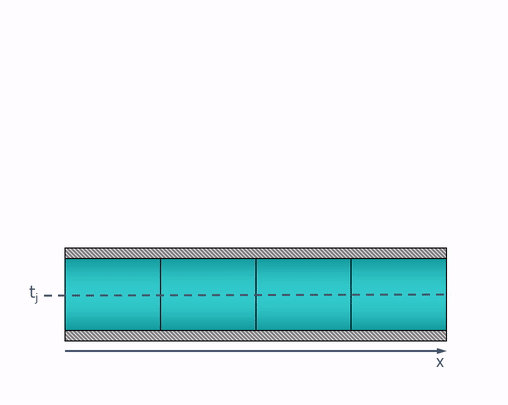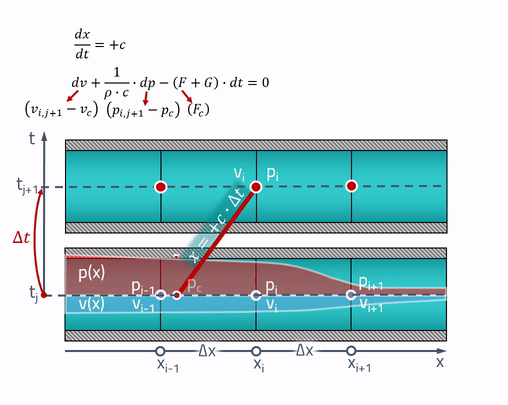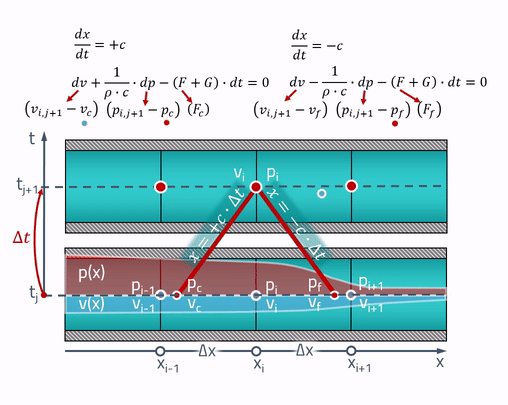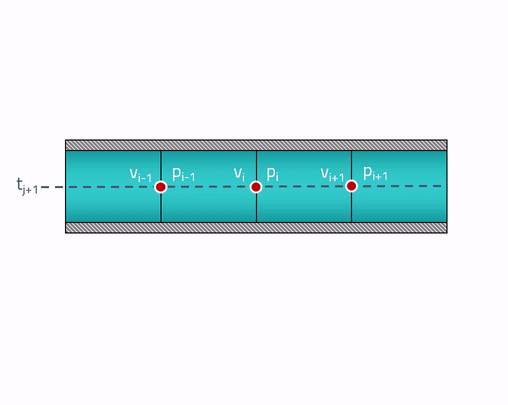
Pour commencer, nous comprendrons l'énoncé du problème. À notre moment initial, nous avons une sorte de distribution des pressions et des vitesses le long de la longueur du tuyau. Tout d'abord, nous divisons le tuyau en un nombre fini d'éléments et attribuons une valeur de pression à chaque face $$$p_i$et la vitesse $$$v_i$.


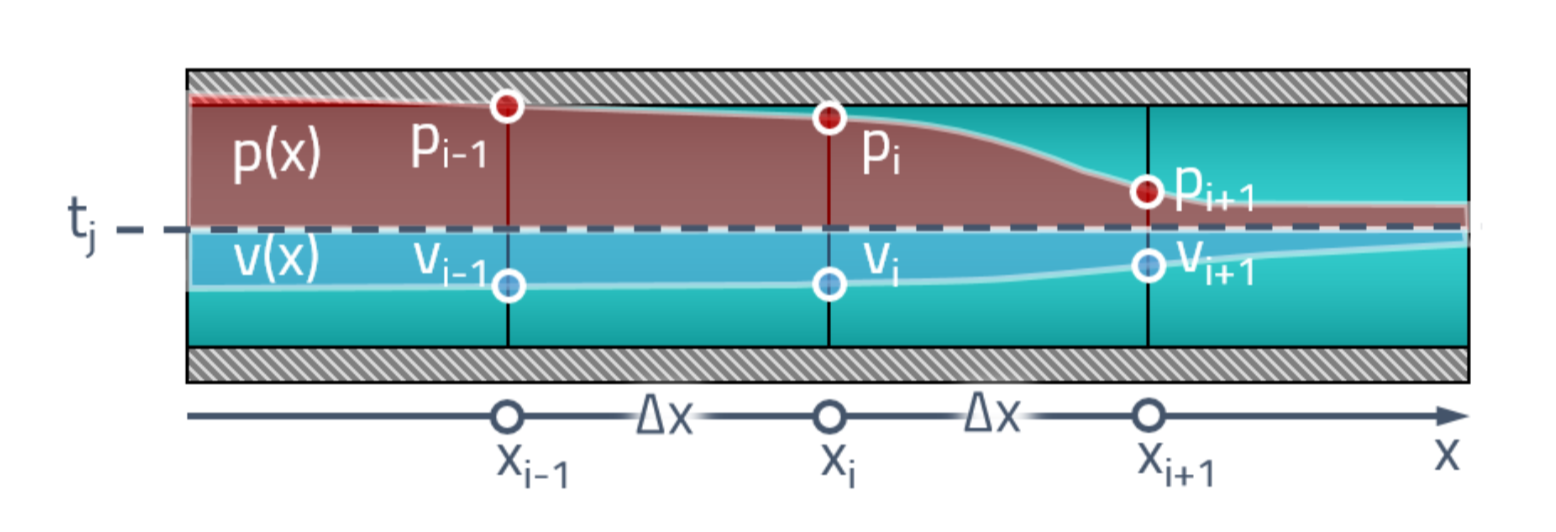
Nous voulons savoir comment les valeurs à ces points changent au fil du temps $$$\ triangle t$. Avancez rapidement dans l'espace-temps et placez l'état du tuyau dans le futur au-dessus de l'état initial:



C'est là que les caractéristiques «magiques» sont utiles! L'explication du paysan qui travaille est que tous les changements dans le tuyau se produisent à la vitesse du son. Pression et vitesse au moment actuel $$$i$dépendent de la pression et de la vitesse aux points du tuyau où l'onde sonore était (serait) $$$\ triangle t$il y a quelques secondes. Ceci est illustré comme suit:



Deux lignes symétriques sont tracées à partir de n'importe quel point, dont la pente est déterminée par la vitesse du son. Telles sont les caractéristiques mêmes le long desquelles les équations différentielles partielles se transforment en équations différentielles ordinaires. Si nous nommons les points où les caractéristiques se croisent avec l'état du tuyau dans le passé comme $$$c$et $$$f$, les équations s'écrivent comme suit:

$$

$$dv + \ frac1 {\ rho c} dp- (F + G) dt = 0 \; for \; \ frac {dx} {dt} = + c$$

$$

$$dv- \ frac1 {\ rho c} dp- (F + G) dt = 0 \; for \; \ frac {dx} {dt} = - c$$

Les valeurs des pressions et vitesses en ces points peuvent être obtenues par interpolation linéaire entre les valeurs des paramètres d'état sur la grille:


Il est important de considérer que ces points doivent toujours se trouver dans les cellules voisines! Pour cela, le pas de temps doit satisfaire au critère Courant - Friedrichs - Levy (CFL):

$$

$$\ triangle t <\ frac {\ triangle x} c$$

Maintenant, au moins le schéma de différence le plus simple peut être appliqué à ces équations:

$$

$$(v_ {i, \; j + 1} -v_c) + \ frac1 {\ rho c} (p_ {i, \; j + 1} -p_c) - (F + G) \ triangle t = 0$$

$$

$$(v_ {i, \; j + 1} -v_f) - \ frac1 {\ rho c} (p_ {i, \; j + 1} -p_f) - (F + G) \ triangle t = 0$$

Dans le système résultant de deux équations, deux inconnues: la pression $$$p_ {i, \; j + 1}$et la vitesse $$$v_ {i, \; j + 1}$. Vous pouvez le résoudre numériquement, mais il n'y a pas de problème particulier pour obtenir une solution analytique. Ensuite, si nous acceptons la constance de la vitesse du son, nous obtenons un schéma de différence complètement explicite.

Pour consolider, je donnerai une animation de la méthode des caractéristiques:

3. Expérience

J'ai eu l'occasion de me souvenir enfin du modèle lorsque j'ai commencé à travailler chez ESI ITI GmbH à Dresde. Une fois, j'ai reçu un ticket au Helpdesk, où les ingénieurs de l' URACA se sont plaints de ne pas pouvoir atteindre la convergence avec l'expérience avec notre «vieille» pipe.
Ils fabriquent des pompes à piston à eau à haute pression, un énorme «Karcher», et aimeraient être en mesure de prédire les effets de résonance possibles en raison de l'inclusion processus de vagues dans le pipeline. Le problème est que de telles pompes, en règle générale, ont très peu de pistons et fonctionnent à basse vitesse (250-500 tr / min):



De ce fait, et également en raison de l'influence de la compressibilité du liquide, le débit est très inégal:



Les lacunes et les non-linéarités rendent difficile la linéarisation et l'analyse du modèle dans le domaine fréquentiel, et les calculs CFD pour une telle tâche tirent à partir d'un canon sur des moineaux. De plus, ils avaient déjà des modèles dans SimulationX, où ils prenaient en compte la dynamique de la partie mécanique de la pompe, l'élasticité du châssis et les caractéristiques du moteur électrique, il serait donc intéressant de voir comment le pipeline affecte cela.

La disposition du banc de test est assez simple:



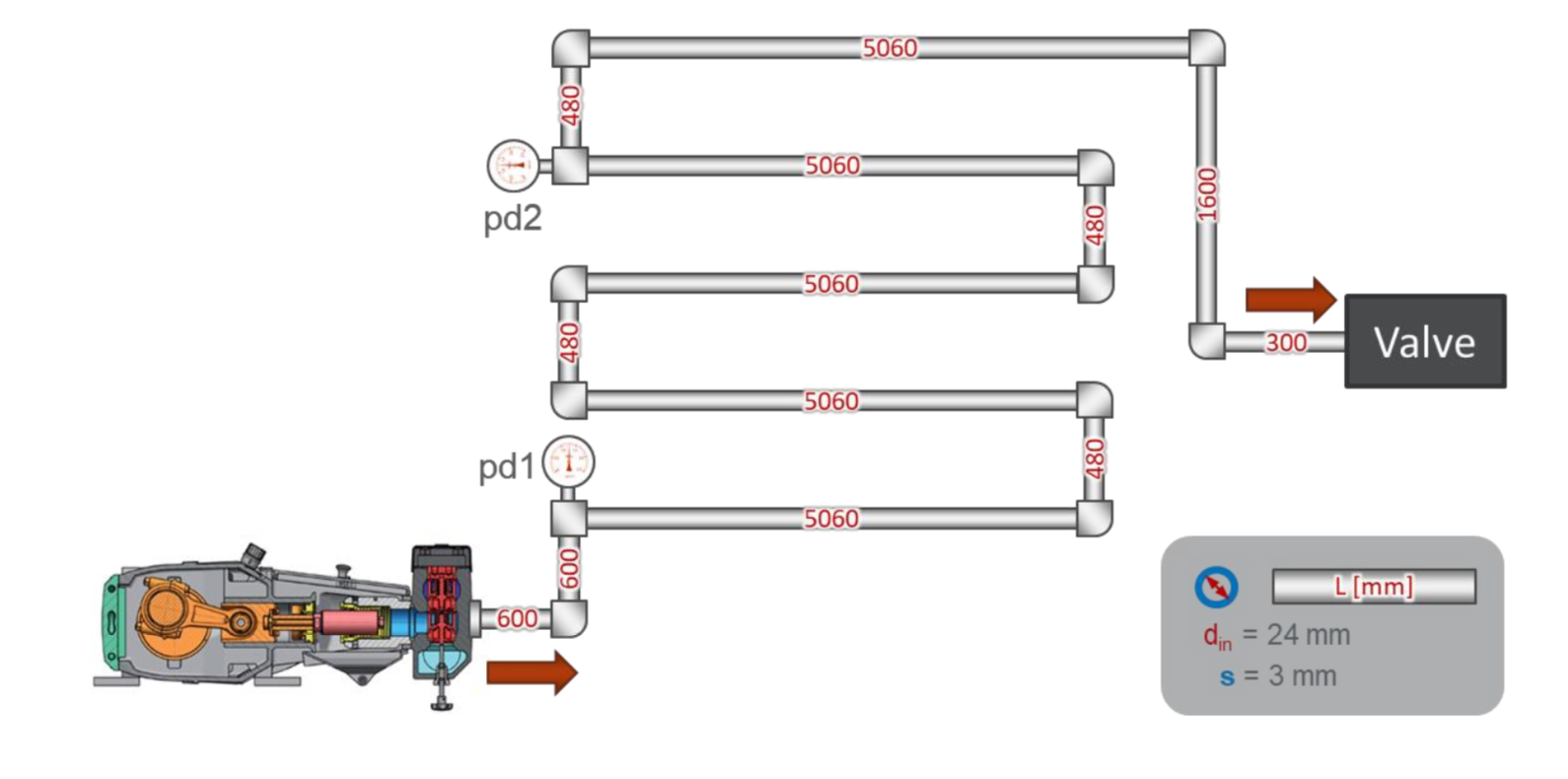
Il existe un simple pipeline d'une longueur totale d'environ 30 mètres. Au début de la canalisation, un capteur de pression pd1 est installé, à une distance de 22 mètres de celui-ci - un capteur de pression pd2. À la fin du pipeline se trouve une vanne qui ajuste la pression dans le système.

J'ai suggéré de tester la version bêta de mon modèle, car un tel modèle a été construit dans SimulationX:



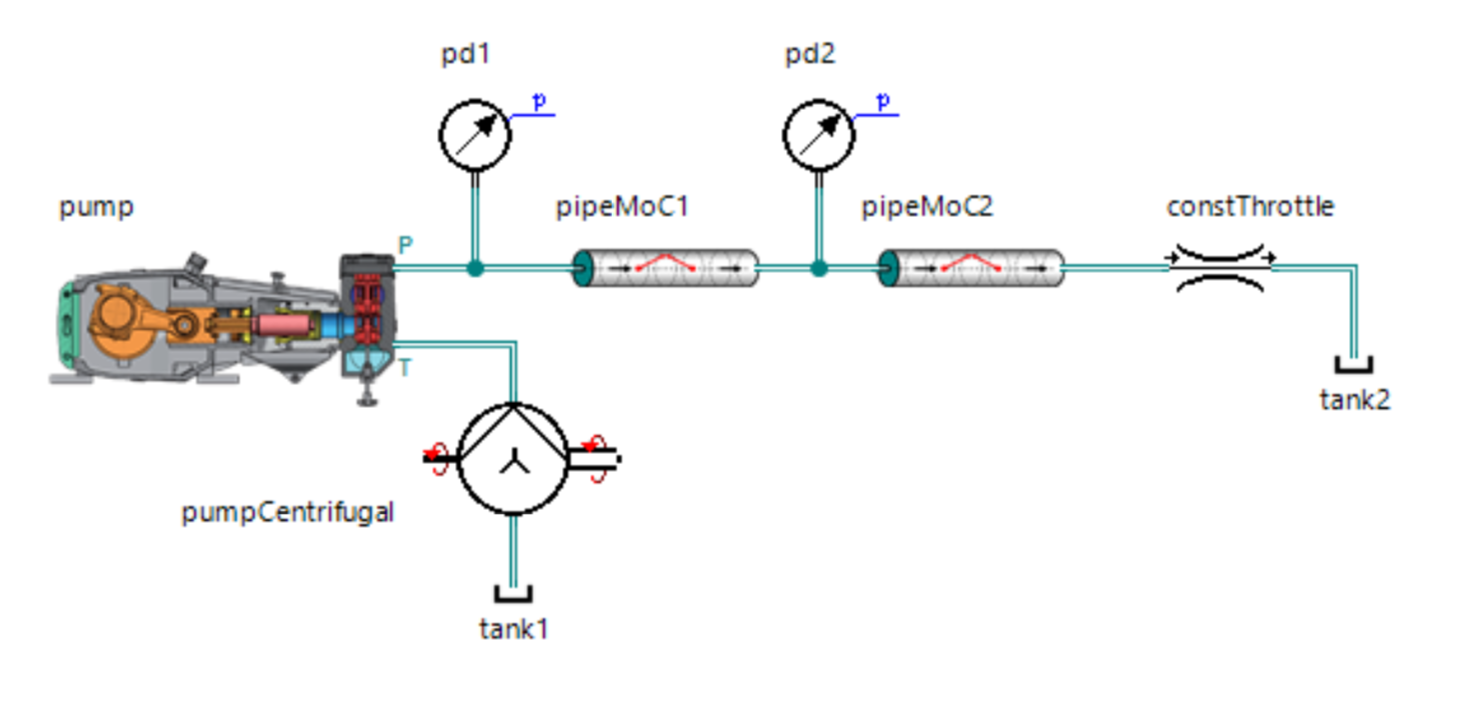
Les résultats m'ont même agréablement surpris:




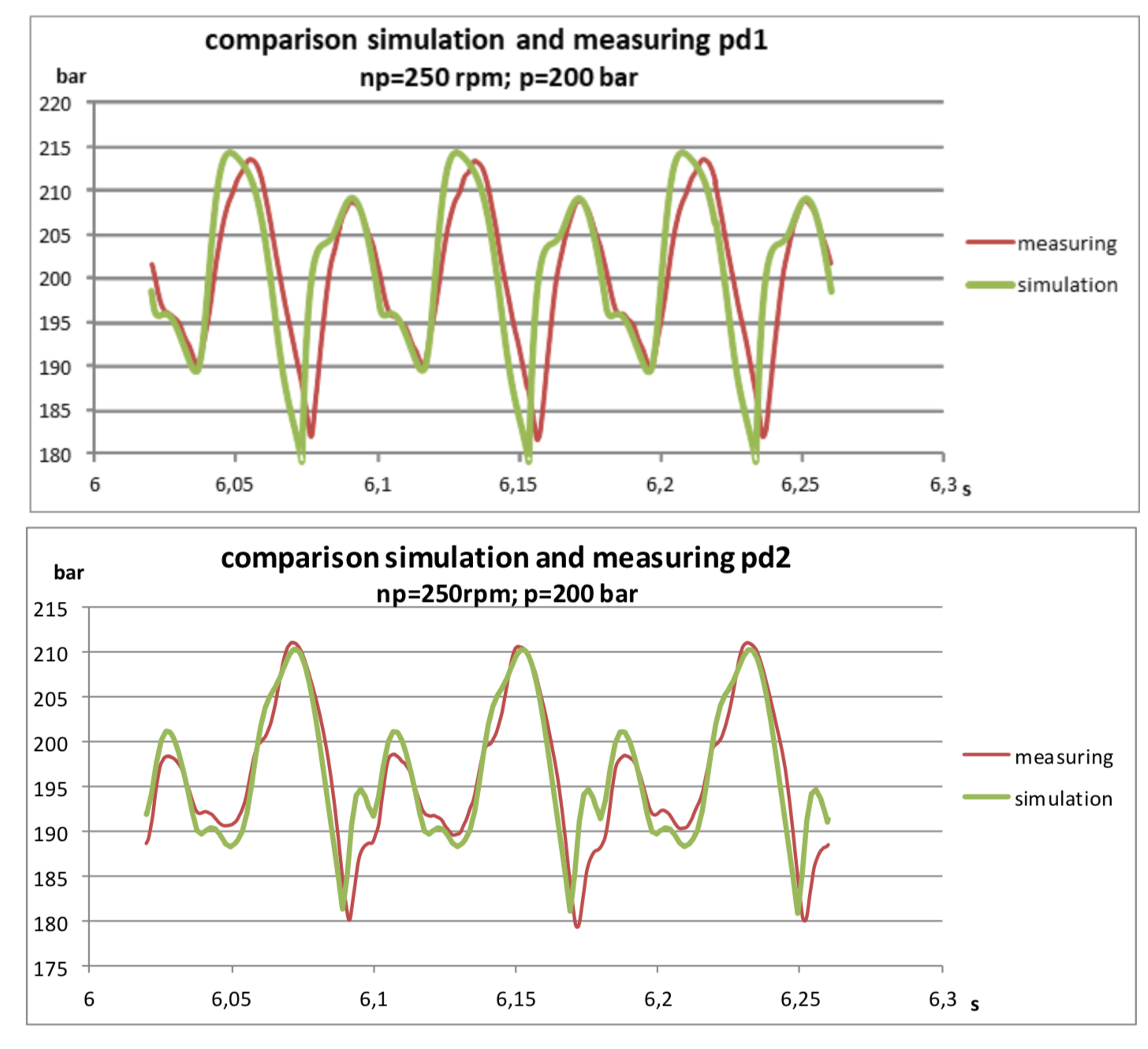
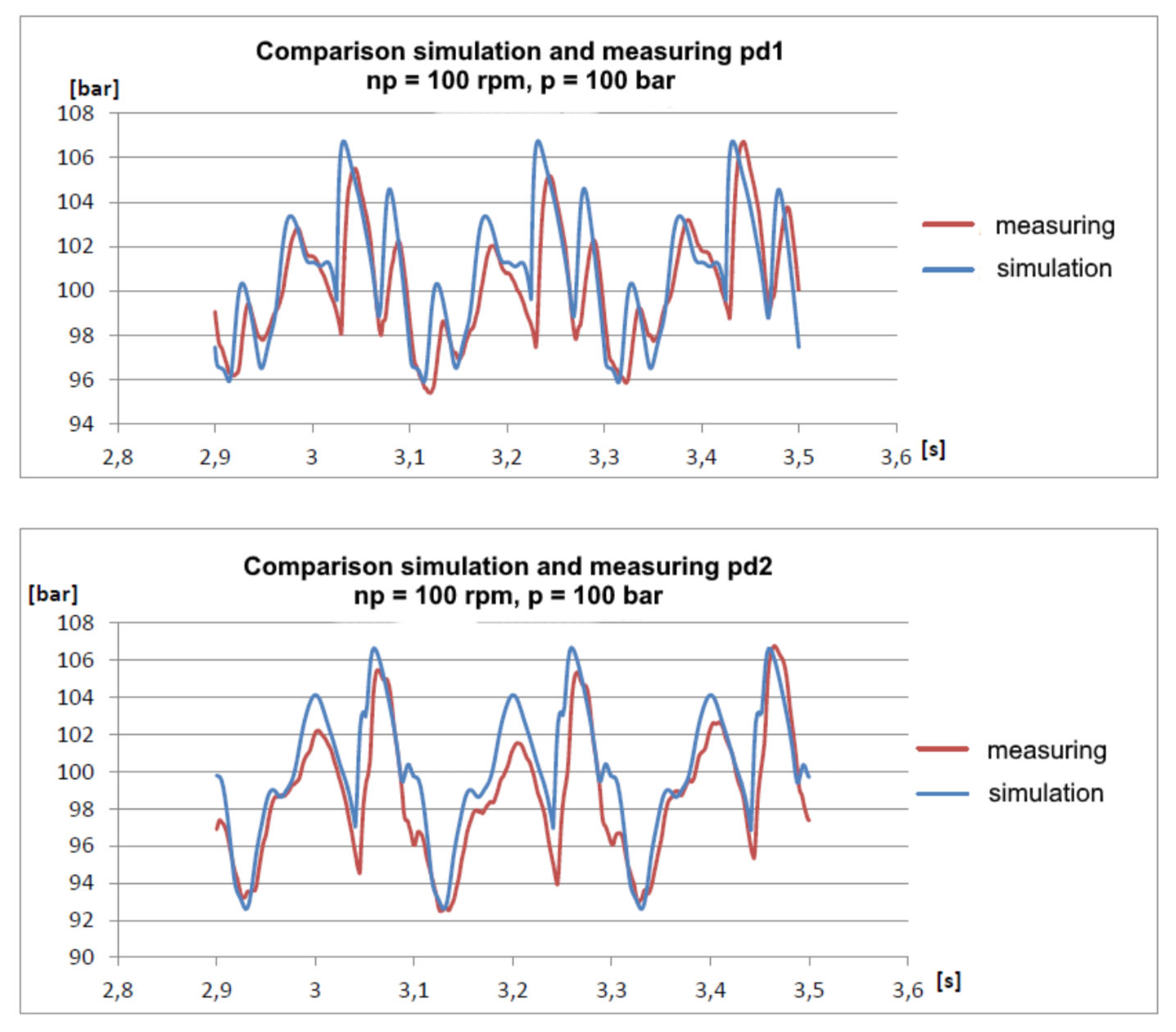
On voit que le modèle est légèrement amorti, ce qui est compréhensible à condition de ne pas tenir compte de la résistance hydraulique. Néanmoins, les harmoniques fondamentales sont assez bonnes en coïncidence et permettent de prédire les amplitudes de pression avec une assez bonne précision.

Cette expérience m'a permis de lancer rapidement un nouveau modèle de ligne hydraulique dans la version SimulationX, et j'ai plongé dans ce sujet et je n'ai pas remarqué comment, avec l'étudiant stagiaire, j'ai également scié le modèle de ligne pneumatique, où tout était beaucoup plus intéressant. Là, j'ai dû utiliser une méthode basée sur la méthode Godunov, qui à son tour est basée sur la solution du problème de Riemann de désintégration d'une discontinuité arbitraire, mais qu'en est-il une autre fois ...

Littérature

1. Dans la littérature nationale, la méthode des caractéristiques pour les applications d'ingénierie est mieux décrite dans le livre "Hydromechanics", D. N. Popov, S. S. Panaiotti, M. V. Ryabinin.
2. Dans sa publication
   Simulation de pipeline par la méthode des caractéristiques pour calculer la pulsation de pression d'une pompe à piston à eau haute pression

   «Dr.-Ing. (Rus) Maxim Andreev, Dipl.-Ing. Uwe Grätz et Dipl.-Ing. (FH) Achim Lamparter ”, The 11th International Fluid Power Conference, 11. IFK, 19-21 mars 2018, Aix-la-Chapelle, Allemagne, voir le texte en PM
   J'ai examiné plus en détail les problèmes de couplage de la méthode des caractéristiques et du solveur de l'ODE.
3. Qui a accès aux bibliothèques allemandes, le meilleur aperçu des méthodes de résolution des équations hyperboliques appliquées aux lignes hydrauliques que j'ai rencontrées est contenu dans la dissertation suivante: Beck, M., Modellierung und Simulation der Wellenbewegung in kavitierenden Hydraulikleitungen, Univ. Stuttgart, Allemagne, 2003.
4. Classics of the genre of hyperbolic equations in general: Randall J. Leveque, Finite Volume Methods for Hyperbolic Problems, Cambridge University Press, Cambridge, Royaume-Uni, 2002.