Bonjour, Habr!

Il y a trois ans, sur le site de Leonid Zhukov, j'ai piqué un lien vers le cours de Yure Leskovek cs224w Analysis of Networks et maintenant nous allons le prendre avec tout le monde dans notre conversation confortable sur le canal # class_cs224w. Immédiatement après un échauffement avec un cours d'apprentissage automatique ouvert qui commence dans quelques jours.

Question: Que lisent-ils là-bas?
Réponse: mathématiques modernes. Nous montrons un exemple d'amélioration du processus de recrutement informatique.

Sous le chat du lecteur, il y a une histoire sur la façon dont les mathématiques discrètes ont conduit un chef de projet vers des réseaux de neurones, pourquoi l'ERP et les chefs de produit devraient lire le magazine Bioinformatics, comment la tâche de recommander des connexions est apparue et est résolue, qui a besoin de représentations graphiques et d'où elles viennent, ainsi que l'opinion selon laquelle comment arrêter d'avoir peur des questions sur les arbres lors des entretiens, et ce que tout cela peut coûter. C'est parti!

Notre plan est le suivant:

1) Qu'est-ce que cs224w
2) Checkered ou ride
3) Comment ai-je pu accéder à tout cela?
4) Pourquoi lire le magazine bioinformatique
5) Qu'est-ce que l'intégration des graphiques et d'où vient-elle
6) Poussette aléatoire sous forme de matrice
7) Le retour d'une poussette aléatoire et la force des liens
8) Le chemin d'un clochard aléatoire et le sommet du vecteur
9) Nos journées sont un clochard aléatoire pour tout le monde et tout le monde
10) Comment et où stocker ces données et où les obtenir
11) De quoi avoir peur
12) Mémo au joueur

Qu'est-ce que CS224W

Le cours de Yure Leskovek Analysis of Networks se démarque dans la galaxie de produits éducatifs de la Faculté des sciences informatiques de l'Université de Stanford. La différence par rapport aux autres est que le programme couvre un très large éventail de questions. C'est la nature interdisciplinaire qui fait de l'aventure un défi. Le prix est le langage universel pour la description des systèmes complexes - la théorie des graphes, qui peut être traité en dix semaines.

Le cours ne coûte pas trop cher, mais ouvre le programme de certificat d'études supérieures en ensembles de données massives sur l' exploitation minière , qui a encore beaucoup de goodies.

Le deuxième dans l'aventure est le Machine Learning CS229 d'Andrew Eun, qui est annoncé inutilement.

Viennent ensuite les ensembles de données massives minières CS246 Jure Leskoveka, dans lesquels ceux qui le souhaitent sont invités à se reposer sur MapReduce et Spark.

Chris Manning termine le banquet CS276 Récupération d'informations et recherche sur le Web.

En prime, le CS246H Mining Massive Data Sets: Hadoop Labs est spécialement conçu pour ceux qui étaient peu nombreux. Visiter à nouveau Yure.

En général, ils promettent que ceux qui ont réussi le programme acquerront des compétences et des connaissances suffisantes pour rechercher des informations sur Internet (sans Google et d'autres comme eux).

Balade ou dames

Il était une fois, mon leader et mentor, à l'époque - STO en Nestlé ukrainien, m'expliquait, jeune et ambitieux, en essayant d'obtenir un MBA pour devenir même une star, la vérité que l'expérience et la connaissance achètent et se vendent sur le marché du travail, et non diplômes et résultats des tests.

La spécialisation décrite ci-dessus peut être complétée en ligne pour un montant symbolique de 18 900 $.

En moyenne, une aventure prend 1-2 ans, mais pas plus de 3. Pour obtenir un certificat, vous devez suivre tous les cours avec une note d'au moins B (3,0).

Il y a une autre manière.

Tout le matériel des cours de Jure Leskovek est publié ouvertement et très rapidement. Par conséquent, ceux qui le souhaitent peuvent souffrir à tout moment opportun, en coordonnant la charge avec les capacités. Particulièrement doué, je recommande d'essayer le mode aventure "C'est Stanford, chéri!" - passant parallèlement au cours - des vidéos de conférences sont publiées en quelques jours, de la documentation supplémentaire est disponible immédiatement, des devoirs et des solutions s'ouvrent progressivement.

Cette saison, après la fin du cours Open Machine Learning sur Habré , qui est utile à prendre comme échauffement, nous organiserons une course dans la classe de canal dédiée # cs_cs224w ods.ai.

Il est recommandé d'avoir les compétences suivantes:

• Fondements des sciences informatiques à un niveau suffisant pour écrire des programmes non triviaux.
• Fondements de la théorie des probabilités.
• Fondements de l'algèbre linéaire.

Comment suis-je arrivé à tout cela?

Il a vécu pour lui-même, n'a pas pris la peine. Gestion de projets d'implémentation SAP . Parfois - il a agi en tant qu'entraîneur de jeu dans sa spécialisation principale - et CRM a tordu les noix. On peut dire que presque personne n'a touché. J'étais engagé dans l'auto-éducation. À un moment donné, j'ai décidé de me spécialiser dans le domaine de la transformation des affaires (ou de la conduite de changements organisationnels). La tâche d'analyser les organisations avant et après le changement est une partie importante de ce travail. Savoir où et où changer aide beaucoup. Comprendre les relations entre les personnes est un facteur de réussite important. Il a passé plusieurs années à étudier les méthodologies "douces" pour la recherche des organisations, mais il ne pouvait toujours pas être satisfait de la question: "Qui va ramasser qui: le commandant en chef du chef comptable, ou est-il plus fort que le reste de l'entrepôt?" Je me demande depuis plusieurs années de suite. Je cherche un moyen de mesurer avec certitude.

2014 a été un tournant, lorsque j'ai abandonné mes rêves de MBA et choisi la statistique et la gestion de l'information à la nouvelle université de Lisbonne (le premier département de télécommunications vivant de la faculté d'aviation et des systèmes spatiaux de l'Université polytechnique de Kiev) comme deuxième plus élevé (j'entends le roulement du tambour) + Département des communications de l'armée).

Au premier semestre de la deuxième magistrature, il a tenté l'analyse des réseaux sociaux - l'une des applications de la théorie des graphes. C'est alors que j'ai appris que c'était quelque chose qui, il s'avère, il existe des algorithmes qui résolvent des problèmes comme qui sera ami avec quelqu'un contre la mise en œuvre de nouvelles technologies, mais je ne le savais pas avant et je me suis essuyé la tête, en analysant les connexions des gens dans mon esprit - ça gonfle vraiment. Il s'est avéré par hasard que l'analyse des réseaux, après les premières étapes, est un creusage continu de données et d'apprentissage automatique, avec ou sans professeur.

Au début, il y avait assez de classiques.

J'en voulais plus. Afin de faire face aux plongements (et de couper le travail de Marinka Zhitnik à leurs tâches), j'ai dû me plonger dans le deep learning, qui a été grandement aidé par le cours de Deep Learning sur les doigts . Compte tenu de la rapidité avec laquelle le groupe Leskovek crée de nouvelles connaissances, pour résoudre automatiquement les tâches managériales, il suffit de suivre simplement leur travail.

Pourquoi lire le magazine bioinformatique

La consolidation d'équipe n'est pas une tâche facile. Qui ne devrait pas être mis dans le même bateau avec un est l'un des problèmes urgents. Surtout quand les visages sont nouveaux. Et la région n'est pas familière. Et pour mener à des rivages lointains, vous n'avez pas besoin d'un bateau, mais d'une flottille entière. Et sur le chemin, une interaction étroite est nécessaire à la fois dans les bateaux et entre eux. Jours ouvrables habituels de mise en œuvre de SAP , lorsque le client doit fournir un système configuré pour ses spécificités à partir d'un tas de modules et que le plan de projet comprend des milliers de lignes. Pour tout son travail, il n'a jamais embauché personne - ils ont toujours formé une équipe. Vous êtes chef de projet, vous avez des pouvoirs et vous vous retournez. Quelque chose comme ça. Tordu.

Exemple de vie:

Je n’ai pas moi-même interviewé, mais j’ai attribué des Timlids pour cela. Et pour les ressources - demande de moi. Et l'intégration des nouveaux membres de l'équipe est également de la responsabilité du chef de projet. Je pense que beaucoup conviendront que plus la liste des candidats est bien préparée, plus le processus sera agréable pour tous les participants. Nous examinerons cette tâche en détail.

Paresse naturelle requise - trouvez un moyen d'automatiser. Je l'ai trouvé. Je partage.

Un peu de théorie de la gestion. La méthodologie Adizes est basée sur un principe de base: les organisations, comme les organismes vivants, ont leur propre cycle de vie et présentent des manifestations comportementales prévisibles et répétitives pendant la croissance et le vieillissement. À chaque étape du développement organisationnel, l'entreprise s'attend à un ensemble spécifique de problèmes. Dans quelle mesure la direction de l'entreprise les gère, avec quel succès elle apporte les changements nécessaires à une transition saine d'étape en étape et détermine le succès ou l'échec ultime de cette organisation.

Je connais les idées de Yitzhak Adizes depuis une dizaine d'années et, à bien des égards, je suis d'accord.

Les personnalités des employés - comme les vitamines - influencent le succès dans certaines conditions. Il existe des exemples connus de la façon dont les dirigeants qui réussissent, passant d'une industrie à une autre, ont échoué. Ça arrive pire. Par exemple, Marissa Mayer, qui a lancé une recherche Google, a abandonné Yahoo. Warren Buffett dit qu'il n'aurait guère réussi à naître au Bangladesh. L'environnement et les moyens d'interagir sont un facteur important.

Ce serait bien de prédire les complications avant d'expérimenter sur un vivant, non?

Dans ce cadre se trouve la prochaine étude de Marinka itnik publiée dans la revue Bioinformatics. La tâche de prédire les effets secondaires avec l'utilisation combinée de médicaments est mathématiquement proche de la gestion. Tout cela grâce à la polyvalence du langage graphique. Examinons-le plus en détail.

Réseau convolutionnel à graphe Decagon - un outil pour prédire les connexions dans les réseaux multimodaux.

La méthode consiste à construire un graphique multimodal des interactions protéine-protéine, médicament-protéine et effets secondaires d'une combinaison de médicaments, qui sont des relations médicament-médicament, où chacun des effets secondaires est un bord d'un certain type. Decagon prédit un type spécifique d'effet secondaire, le cas échéant, qui apparaît dans le tableau clinique.

La figure montre un exemple de graphique des effets secondaires obtenus à partir des données du génome et de la population. Au total - 964 différents types d'effets secondaires (indiqués par des côtes de type ri, i = 1, ..., 964). Des informations supplémentaires dans le modèle sont présentées sous forme de vecteurs des propriétés des protéines et des médicaments.

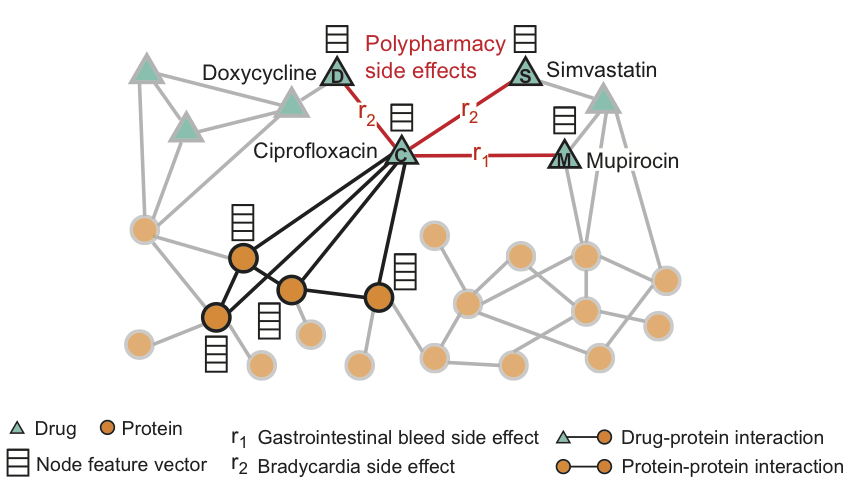
Pour le médicament Ciprofloxacine (nœud C), les voisins mis en évidence dans le graphique reflètent les effets sur quatre protéines et trois autres médicaments. Nous voyons que la ciprofloxacine (nœud C), prise simultanément avec la doxycycline (nœud D) ou la simvastatine (nœud S), augmente le risque d'un effet secondaire de ralentir la fréquence cardiaque (un effet secondaire comme r2), et une combinaison avec la mupirocine (M) - augmente le risque de saignement du tractus gastro-intestinal (effet secondaire type r1).

Decagon prédit les associations entre les paires de médicaments et les effets secondaires (indiqués en rouge) pour identifier les effets secondaires d'une utilisation simultanée, c'est-à-dire les effets secondaires qui ne peuvent être associés à aucun des médicaments de la paire séparément.

Architecture du graphe de réseaux de neurones convolutifs Decagon:

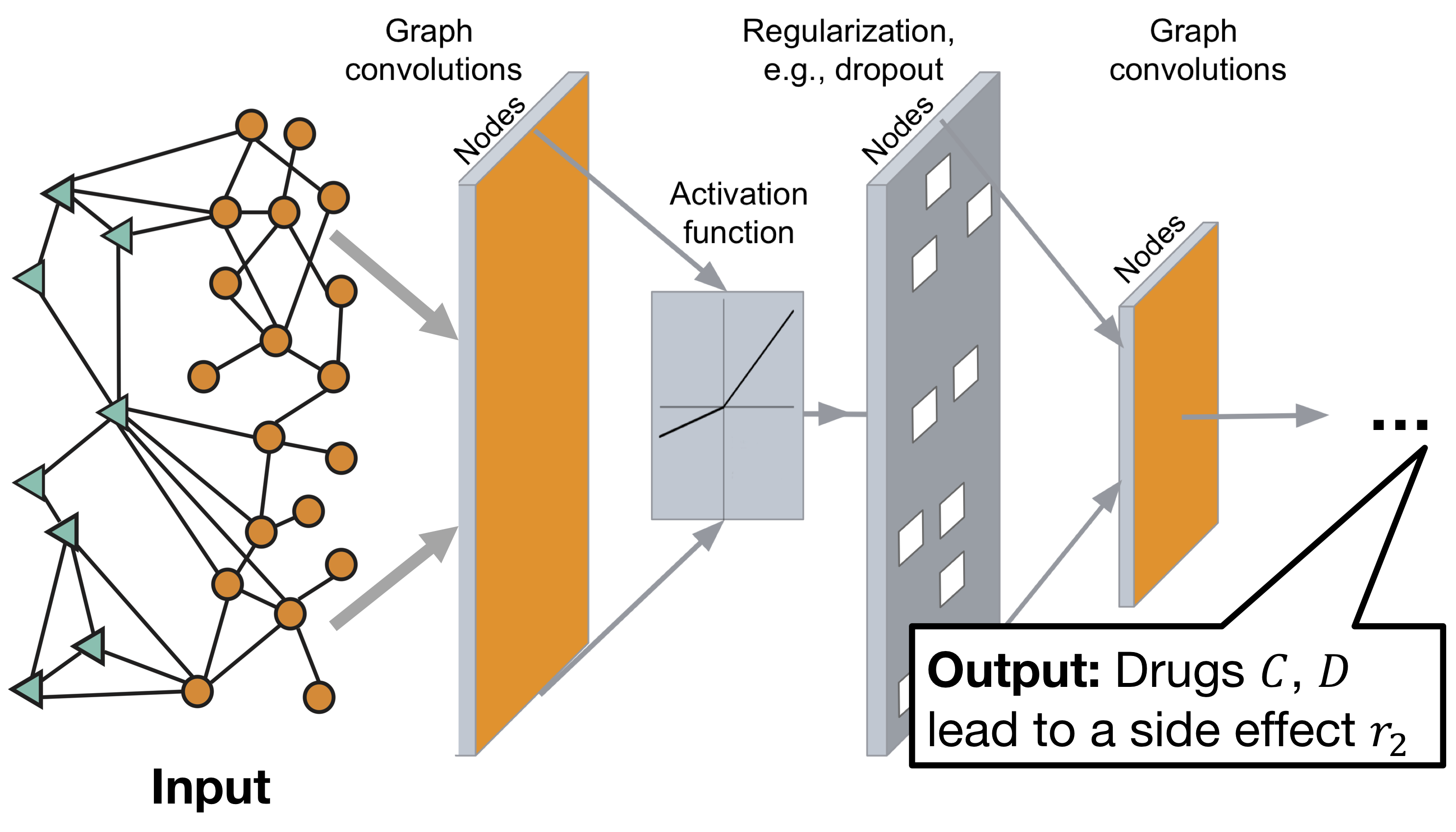
Le modèle se compose de deux parties:

Encodeur: réseau convolutionnel de graphes (GCN) recevant un graphe et embarqué pour les nœuds,
Décodeur: un modèle de factorisation tensorielle qui utilise ces plongements pour détecter les effets secondaires.

Plus d'informations peuvent être trouvées sur le site Web du projet ou ci-dessous.

Génial, mais comment lier cela à l'esprit d'équipe?

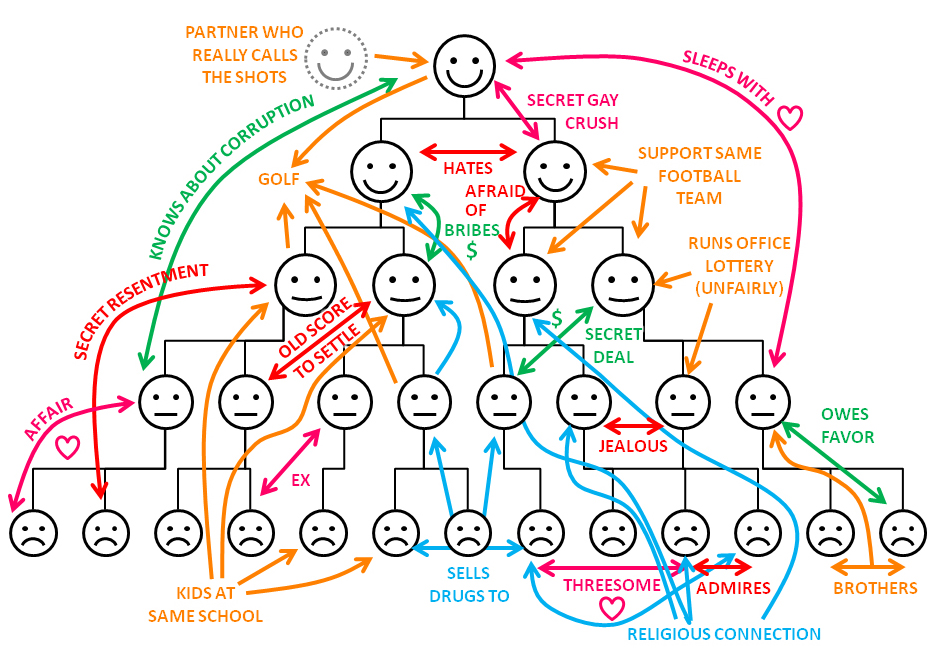
Quelque chose comme ça .

Ici, afin de se sentir à l'aise dans un domaine de recherche similaire à celui décrit, il vaut la peine de déterrer le granit de la science. Certes, creuser se fera de manière intensive - la théorie des graphes se développe activement. C'est pourquoi c'est le fer de lance du progrès - peu de gens y sont à l'aise.

Pour comprendre les détails du fonctionnement de Decagon, nous allons faire une excursion dans l'histoire.

Qu'est-ce que l'intégration de graphiques et d'où vient-elle?

Il m'est arrivé d'observer un changement dans l'ensemble des méthodes avancées pour résoudre les problèmes de prédiction des connexions sur les graphiques au cours des quatre dernières années. C'était amusant. Presque comme dans un conte de fées - le plus loin, le pire. L'évolution a suivi le chemin de l'heuristique qui a déterminé l'environnement pour le haut du graphique aux poussettes aléatoires, puis des méthodes spectrales (analyse matricielle) sont apparues, et maintenant des réseaux de neurones.

Nous formulons le problème de la prédiction des relations:

Considérons un graphique non orienté$$ $ inline $ \ begin {align *} G (V, E) \ end {align *} $ inline $ où
$$$ inline $ \ begin {align *} V \ end {align *} $ inline $ - de nombreux sommets$$ $ inline $ \ begin {align *} v \ end {align *} $ inline $ ,
$$$ inline $ \ begin {align *} E \ end {align *} $ inline $ - de nombreuses côtes$$ $ inline $ \ begin {align *} e (u, v) \ end {align *} $ inline $ reliant les pics$$ $ inline $ \ begin {align *} u \ end {align *} $ inline $ et$$ $ inline $ \ begin {align *} v \ end {align *} $ inline $ .

Nous définissons l'ensemble de toutes les arêtes possibles$$ $ inline $ E ^ {\ diamond} $ inline $ sa puissance
$$$ inline $ \ begin {align *} | E ^ {\ diamond} | & = \ frac {| V | * (| V | - 1)} {2} \\ \ end {align *} $ inline $ où
$$$ inline $ \ begin {align *} | V | = n \ end {align *} $ inline $ , Est le nombre de sommets.

De toute évidence, de nombreux bords inexistants peuvent être exprimés comme$$ $ inline $ \ begin {align *} \ overline {E} = E ^ {\ diamond} - E \ end {align *} $ inline $ .

Nous supposons que dans l'ensemble$$ $ inline $ \ begin {align *} \ overline {E} \ end {align *} $ inline $ il y a des liens manqués, ou des liens qui apparaîtront à l'avenir, et nous voulons les trouver.

La solution se résume à définir une fonction$$ $ inline $ \ begin {align *} D (u, v) \ end {align *} $ inline $ la distance entre les sommets du graphique, permettant la structure du graphique$$ $ inline $ \ begin {align *} G (t_0, t_0 ^ \ star) \ end {align *} $ inline $ fixé sur une période de temps$$ $ inline $ \ begin {align *} (t_0, t_0 ^ \ star) \ end {align *} $ inline $ prédire l'apparence des bords$$ $ inline $ \ begin {align *} G (t_1, t_1 ^ \ star) \ end {align *} $ inline $ dans la gamme$$ $ inline $ \ begin {align *} (t_1, t_1 ^ \ star) \ end {align *} $ inline $ .

L'une des premières publications qui proposait de passer du clustering à la tâche de prédire les relations dans le contexte de l'étude de l'expression des gènes communs est parue dans la revue (comme vous pouvez le deviner) Bioinformatics en 2000. Déjà en 2003, un article de John Kleinberg a été publié avec un aperçu des méthodes pertinentes pour résoudre le problème de la prévision des connexions dans un réseau social. Son livre " Networks, Crowds, and Markets: Reasoning About a Highly Connected World " est un manuel qu'il est recommandé de lire pendant le cours cs224w, la plupart des chapitres sont répertoriés dans la section de lecture requise.

Un article peut être considéré comme une tranche de connaissances dans un domaine étroit, comme nous le voyons, au début, l'assortiment de méthodes était petit et comprenait:

• Méthodes basées sur les voisins de graphe - et la plus évidente d'entre elles est le nombre de voisins communs.

Nous donnons la définition:

Haut$$ $ en ligne $ u $ en ligne $ est un voisin graphique pour le haut$$ $ inline $ v $ inline $ si côte$$ $ inline $ e (u, v) \ in E $ inline $ .

Nous dénotons$$ $ inline $ \ Gamma (u) $ inline $ de nombreux sommets voisins$$ $ en ligne $ u $ en ligne $ ,

puis la distance entre les pics$$ $ en ligne $ u $ en ligne $ et$$ $ inline $ v $ inline $ peut s'écrire

$$$ inline $ D_ {CN} (u, v) = \ Gamma (u) \ cap \ Gamma (v) $ inline $ .

Intuitivement, plus l'intersection des ensembles de voisins de deux sommets est grande, plus la connexion entre eux est probable, par exemple, la plupart des nouvelles connaissances se produisent avec des amis d'amis.

Heuristique plus avancée - coefficient Jacquard$$ $ inline $ D_J (u, v) = \ frac {\ Gamma (u) \ cap \ Gamma (v)} {\ Gamma (u) \ cup \ Gamma (v)} $ inline $ (qui avait déjà cent ans) et récemment (à cette époque) la distance proposée Adamik / Adar$$ $ inline $ D_ {AA} (u, v) = \ sum_ {x \ in \ Gamma (u) \ cap \ Gamma (v)} \ frac {1} {\ log | \ Gamma (x) |} $ inline $ développer l'idée par des transformations simples.

• Méthodes basées sur des chemins le long d'un graphique - l'idée est que le chemin le plus court entre deux sommets sur un graphique correspond à la chance d'une connexion entre eux - plus le chemin est court, plus la chance est élevée. Vous pouvez aller plus loin et prendre en compte non seulement le chemin le plus court, mais aussi tous les autres chemins possibles entre des paires de pics, par exemple, peser les chemins, comme le fait la distance de Katz . Déjà alors, la longueur de chemin attendue d'un clochard aléatoire est mentionnée - le précurseur de la méthode de recommandation d'amis Facebook.

Estimez la qualité des prévisions:

• Pour chaque paire de sommets$$ $ inline $ (u, v) $ inline $ chaque côte inexistante$$ $ inline $ e (u, v) \ in \ overline {E} $ inline $ calculer la distance$$ $ en ligne $ D (u, v) $ en ligne $ sur le graphique$$ $ inline $ G (t_0, t_0 ^ \ star) $ inline $ .
• Trier les paires$$ $ inline $ (u, v) $ inline $ distance décroissante$$ $ en ligne $ D (u, v) $ en ligne $ .
• À emporter$$ $ en ligne $ m $ en ligne $ paires avec les valeurs les plus élevées est notre prévision.
• Voyons combien de bords prédits sont apparus dans$$ $ inline $ G (t_1, t_1 ^ \ star) $ inline $ .

Il est important de se rappeler que le nombre de voisins communs et la distance Adamik / Adar sont des méthodes puissantes qui spécifient le niveau de base de la qualité des prévisions uniquement pour la structure du lien, et si votre système de recommandation affiche un résultat plus faible, alors quelque chose ne va pas.

En règle générale, les incorporations de graphiques sont un moyen de représenter les graphiques de manière compacte pour les tâches d'apprentissage automatique à l'aide de la fonction de transformation$$ $ inline $ \ begin {align *} \ phi: G (V, E) \ longmapsto \ mathbb {R} ^ d \ end {align *} $ inline $ .

Nous avons examiné plusieurs de ces fonctions, la plus efficace de la première. Une liste plus large est décrite dans un article de Kleinberg. Comme nous pouvons le voir dans la revue, même alors, ils ont commencé à appliquer des méthodes de haut niveau, telles que la décomposition matricielle, le regroupement préliminaire et les outils de l'arsenal de la linguistique computationnelle. Il y a quinze ans, tout ne faisait que commencer. Les plongements étaient unidimensionnels.

Poussette aléatoire en forme de matrice

L'étape suivante sur le chemin vers les mêmes plongements graphiques a été le développement de méthodes de marche aléatoire. Inventer et justifier de nouvelles formules pour calculer la distance est apparemment devenu une rupture. Dans certaines applications, il semble que vous deviez simplement compter sur le hasard et faire confiance aux vagabonds.

Nous donnons la définition:

Matrice d'adjacence graphique$$ $ en ligne $ g $ en ligne $ avec un nombre fini de sommets$$ $ en ligne $ n $ en ligne $ (numéroté de 1 à$$ $ en ligne $ n $ en ligne $ ) Est une matrice carrée$$ $ inline $ a $ inline $ la taille$$ $ en ligne $ n \ fois n $ en ligne $ dans lequel la valeur de l'élément$$ $ inline $ a_ {ij} $ inline $ égal au poids$$ $ inline $ w_ {ij} $ inline $ côtes$$ $ en ligne $ e (i, j) $ en ligne $ .

Remarque: ici, nous nous éloignons intentionnellement des indicateurs de sommet utilisés précédemment$$ $ inline $ u, v $ inline $ et nous utiliserons la notation familière à l'algèbre linéaire et, en général, pour travailler avec des matrices$$ $ en ligne $ i, j $ en ligne $ .

Nous illustrons les concepts considérés:

Soit$$ $ en ligne $ g $ en ligne $ - graphique de quatre sommets$$ $ inline $ \ {A, B, C, D \} $ inline $ reliés par des nervures.

Afin de simplifier les constructions, nous supposons que les bords de notre graphe sont bidirectionnels, c'est-à-dire$$ $ inline $ \ forall e (i, j) \ in E, \ exist e (j, i) \ in E \ land w_ {ij} = w_ {ji} $ inline $ .

$$$ en ligne $ e (A, B), w_ {AB} = 1; \\ e (B, C), w_ {BC} = 2; \\ e (A, C), w_ {AC} = 3; \ \ e (B, C), w_ {BC} = 1. $ en ligne $

Nous représentons les ensembles d'arêtes:$$ $ en ligne $ E $ en ligne $ - en bleu, et$$ $ inline $ \ overline {E} $ inline $ - en vert.



$$$ inline $ \ begin {align *} A = \ left [\ begin {matrix} 0 & 1 & 3 & 0 \\ 1 & 0 & 2 & 1 \\ 3 & 2 & 0 & 0 \\ 0 & 1 & 0 & 0 \ end {matrice} \ droite] \ end {align *} $ inline $

L'écriture d'un graphique sous forme matricielle ouvre des possibilités intéressantes. Pour les démontrer, jetez un œil au travail de Sergey Brin et Larry Page, et voyez comment PageRank, un algorithme pour classer les sommets des graphes, est toujours un élément important de la recherche Google.

PageRank - inventé pour rechercher les meilleures pages sur Internet. Une page est considérée comme bonne si elle est appréciée (liée à) par d'autres bonnes pages. Plus il y a de pages contenant des liens vers celle-ci, et plus leur note est élevée, plus le PageRank est élevé pour une page donnée.

Considérez l'interprétation de la méthode à l'aide de chaînes de Markov .

Nous donnons une définition: Le

degré d'un sommet (degré) est la puissance de nombreux voisins:
$$$d_i = |\Gamma(i)|$,

Distinguer entre degré et hors degré. Pour notre exemple, ils sont équivalents.

Nous construisons une matrice d'adjacence pondérée, guidée par la règle:
$$$\begin{align*}M_{ij} = \left\{ \begin{matrix} \frac{1}{d_j} & \forall i,j \iff i \in \Gamma(j), \\ 0 & \forall i,j \iff i \notin \Gamma(j). \end{matrix} \right.\end{align*}$

$$$\begin{align*}M = \left[ \begin{matrix} 0 & \frac{1}{3} & \frac{1}{2} & 0 \\ \frac{1}{2} &0 & \frac{1}{2} & 1 \\ \frac{1}{2} & \frac{1}{3} & 0 & 0\\ 0 & \frac{1}{3} & 0& 0 \end{matrix} \right]\end{align*}$

, $$$M$1 (.. $$$M$— " "). $$$j$$$$i \in \Gamma(j)$.

$$$r_i$PageRank $$$i$, $$$d_i$. PageRank $$$j$comment

$$

$$r_j = \sum_{i \to j}\frac{r_i}{d_i}$$

, $$$i$$$$j$PageRank, (.. PageRank), .

PageRank $$$\begin{align*}r = [r_1, r_2, ..., r_n]^T \end{align*}$— :

$$

$$r = Mr$$

-, ( ). $$$t$$$$i$$$$t+1$$$$j \in \Gamma(i)$, , — .

Nous dénotons $$$p(t)$, $$$i$$$$t$. $$$p(t)$— , 1.

, $$$M_{ij}$— $$$j$$$$i$, $$$j$$$$p_j(t)$— , $$$j$$$$t$. , $$$i$

$\$\$display\$\$p\_i(t+1)\; =\; M\_\{i1\}p\_1(t)\; +\; M\_\{i2\}p\_2\; +\; .$. . + M_{in}p_n(t)$$display$$

,

$$

$$p(t + 1) = Mp(t)$$

- , $$$p(t + 1) = p(t)$, $$$p(t)$— . , PageRank $$$r = Mr$. — $$$r$PageRank — !

$$$r$PageRank . , $$$r^{(t0)} = [1/n, 1/n, ..., 1/n]^T$$$$r^{(t+1)} = Mr^{(t)}$$$$t$, , .. $$$||r^{(t+1)} - r^{(t)}||_1 < \epsilon$où $$$\epsilon$— . ( , $$$||x||_1 = \sum_{k} |x_k|$— $$$L_1$, ). $$$r^{(t+1)}$Page Rank . , 20-30 .

.

"" :

• .. " " — , — , PageRank . . .
• — — PageRank . - . $$$r$.

20 , !

- $$$\beta$, $$$1 - \beta$— . $$$1 - \beta \approx 0.15$, .. - 5-7 . — . PageRank :

$$

$$r_j = \sum_{i \to j}\beta\frac{r_i}{d_i} + (1-\beta)\frac{1}{n}$$

( , )

$$$M$,

$$

$$M^{\star} = \beta M + (1-\beta) [1/n]_{n×n}$$

. $$$r = M^{\star}r$. , , 37-38 14- cs224w 2017 , , Pinterest ( ).

. ?

:

• ;
• ;
• , .

PageRank. , , - , - .

— .

.

, . - ? 2006 .

:

, - $$$G$, - .

$$$i$$$$k$$$$f^{(i)} = [f_1, f_2, ..., f_k]^T$.



, $$$f_1$, , .

, , . - . , — (, ). , IT- , ( ) — .

, , — , , $$$A$$$$C$— .

, — .

- , Kaggle Hackerrank, , , (, ).

:

$$$S_k(x)$$$$x$$$$k$, $$$G$:

$$$\forall i \in V, i \in S_k(x) \iff f^{(i)}_{k} = x$

:

$$$\begin{align*}M^{p}_{ij} = \left\{ \begin{matrix} \beta M_{ij} + \frac{1-\beta}{|S_k(x)|} & \forall i,j \iff i \in S_k(x), \\ \beta M_{ij} & \forall i,j \iff i \notin S_k(x). \end{matrix} \right.\end{align*}$

$$$\begin{align*} r = M^{p} r \end{align*}$$$$\begin{align*} r \end{align*}$, . $$$\begin{align*} r \end{align*}$PageRank — . , $$$\begin{align*} r \end{align*}$— .

80% Pinterest.

, $$$\begin{align*}|S_k(x)| = 1\end{align*}$, appelé Random Walks with Restarts - les poussettes reviennent et reviennent à un pic qui nous intéresse. En conséquence, nous obtenons une mesure de proximité pour chaque sommet du graphique par rapport à celui-là seulement. Et cela résout le problème de prédire les connexions mieux que la distance Adamik / Adar ne le permet.

Ajoutez d'autres améliorations:

Rappelons que les côtes$$ $ inline $ \ begin {align *} e (i, j) \ in E \ in G \ end {align *} $ inline $ notre graphique a des poids$$ $ inline $ \ begin {align *} w_ {ji} \ end {align *} $ inline $ .

Cela vous permettra de spécifier une matrice pondérée$$ $ inline $ \ begin {align *} M ^ w \ end {align *} $ inline $ probabilités de transition:

$$$ inline $ \ begin {align *} M ^ {w} _ {ij} = \ left \ {\ begin {matrix} \ frac {w_ {ij}} {\ sum_ {j} w_ {ij}} & \ forall i, j \ iff e (i, j) \ in E, \\ 0 & \ forall i, j \ iff e (i, j) \ notin E. \ end {matrix} \ right. \ end {align *} $ inline $

Le clochard fera des transitions, comme auparavant, par accident, mais ce n'est plus tout aussi probable!

Un lecteur attentif s'est déjà demandé comment mesurer ces poids.

Facebook a été intrigué par la même chose en 2011. Il était nécessaire de construire un système de recommandation pour les amis d'amis d'amis, au point de maximiser la création de nouvelles connexions. Et la première étape a été de créer un graphique pondéré des connexions entre les utilisateurs à partir des informations de leurs profils et de l'historique des interactions (likes, messages, photos conjointes, etc.). Mesurer en quelque sorte le pouvoir de l'amitié sur Internet.

$$$$ afficher $$ w_ {ij} = f ^ w (i, j) = e ^ {- \ sum_ {z} {\ xi_z x_ {ij} [z]}}, $$ afficher $$

où$$ $ inline $ \ begin {align *} x_ {ij} \ end {align *} $ inline $ Est le vecteur des propriétés des sommets et des arêtes qui les relient, c'est-à-dire$$ $ inline $ \ begin {align *} x_ {ij} = f ^ {(i)} \ cup f ^ {(j)} \ cup f ^ {e (ij)} \ end {align *} $ inline $ et$$ $ inline $ \ begin {align *} \ xi \ end {align *} $ inline $ Est le vecteur de poids à apprendre des données.

Ici, un lecteur formé reconnaîtra un modèle linéaire et un lecteur non préparé pensera au fait qu'il vaut la peine de suivre un cours d'apprentissage automatique pour traiter la descente de gradient, avec lequel nous apprendrons les valeurs des poids dans un vecteur$$ $ inline $ x_ {ij} $ inline $ - ils montreront comment les goûts et les messages affectent les amitiés sur Internet.

Pourquoi avons-nous besoin de tout cela?

En plus du fait que l'approche envisagée nous permet de prédire encore mieux les connexions, nous pouvons apprendre les règles d'un team building réussi. Et découvrez ce qu'il faut rechercher à l'avenir.

Rappelez-vous les conditions de notre exercice. Nous observons le développement de la coopération (participation conjointe à des compétitions) dans un groupe de données conditionnelles dans l'intervalle$$ $ inline $ \ begin {align *} (t_0, t_0 ^ \ star) \ end {align *} $ inline $ (par exemple, un mois civil) et nous voulons prédire la constitution d'une équipe dans l'intervalle$$ $ inline $ \ begin {align *} (t_1, t_1 ^ \ star) \ end {align *} $ inline $ (encore un mois). En plus de participer à des concours, nous suivons la communication sur les forums, les goûts de noyaux et ce que vous aimez d'autre. Toutes les informations collectées sont stockées dans une matrice$$ $ inline $ X ^ {\ star} \ in \ mathbb {R} ^ {(2k + l) \ times | E |} $ inline $ (ses colonnes sont des vecteurs$$ $ inline $ x_ {ij} $ inline $ ,$$ $ inline $ k, l $ inline $ - dimensions des vecteurs de propriétés des sommets et arêtes$$ $ inline $ f ^ {(i)}, f ^ {e (ij)} $ inline $ , respectivement) et le graphique$$ $ inline $ \ begin {align *} G \ end {align *} $ inline $ pendant deux intervalles de temps.

Préparons les données pour l'apprentissage automatique.

Pour chaque sommet$$ $ inline $ \ begin {align *} i \ end {align *} $ inline $ :

1) définir de nombreux amis d'amis:

$$$$ afficher $$ \ Gamma ^ {fof} (i) = \ bigcup_ {j \ in \ Gamma (i)} \ Gamma (j) - \ Gamma (i) $$ afficher $$

2) et construire des sous-graphiques$$ $ inline $ \ begin {align *} G ^ {fof} (i) \ end {align *} $ inline $ des relations avec des amis et des amis d'amis,$$ $ inline $ \ begin {align *} \ forall e (x, y) \ in E, e (x, y) \ in G ^ {fof} (i) \ iff x, y \ in \ Gamma ^ {fof} (i) \ cup \ Gamma (i) \ end {align *} $ inline $

3) sélectionnez l'ensemble des sommets,$$ $ inline $ \ begin {align *} D_i: \ {d_1, ..., d_k \} \ end {align *} $ inline $ avec qui nous avons noué des liens sont nos exemples positifs d'apprentissage,

4) toutes les connexions non aléatoires de l'ensemble$$ $ inline $ \ begin {align *} \ overline {D_i} = \ Gamma ^ {fof} (i) - D_i \ end {align *} $ inline $ - Ce sont nos exemples négatifs de formation.

Notre tâche consiste à sélectionner un tel vecteur de poids$$ $ inline $ \ begin {align *} \ xi \ end {align *} $ inline $ dans lequel des exemples positifs de l'ensemble$$ $ inline $ \ begin {align *} D_i \ end {align *} $ inline $ obtiendra une valeur de PageRank personnalisé plus élevée par rapport à$$ $ inline $ \ begin {align *} i \ end {align *} $ inline $ que des exemples négatifs.

Pour ce faire, nous définissons la fonction de perte, que nous minimiserons:

$$$$ afficher $$ L = \ sum_ {i} \ sum_ {d \ in D_i, \ overline {d} \ in \ overline {D_i}} h (r _ {\ overline {d}} - r_ {d}) + \ lambda || \ xi || ^ 2, $$ afficher $$

où$$ $ inline $ h (x) = 0 \ ssi x <0; h (x) = x ^ 2 \ ssi x \ geqslant 0; $ en ligne $ - pénalité pour violation des conditions,$$ $ inline $ \ lambda $ inline $ - puissance$$ $ en ligne $ L_2 $ en ligne $ régularisation des poids$$ $ inline $ \ xi $ inline $ ,$$ $ en ligne $ r $ en ligne $ Est un vecteur avec des solutions de l'équation$$ $ inline $ r = M ^ wr $ inline $ concernant$$ $ en ligne $ r $ en ligne $ pour un sous-graphe d'amis d'amis d'un seul sommet$$ $ en ligne $ i $ en ligne $ .

Un détail amusant - le gradient de cette fonction est calculé de la même manière que PageRank, par la méthode d'alimentation. Les détails se trouvent dans la 17e conférence de l'édition 2014, diapositives 9-27.

Voici à quoi ressemblait le fer de lance du progrès lors de ma première connaissance du cours cs224w.

Chemin de poussette aléatoire et haut en vecteur

Et puis vint le triomphe de la paresse!

On sait que la théorie des graphiques a été inventée par Leonard Euler quand il s'ennuyait à résoudre le problème insoluble des ponts qui se trouvent actuellement à Kaliningrad. Au lieu de se sécher la tête pour rien, il a inventé un appareil mathématique qui lui permet de prouver l'impossibilité fondamentale de résoudre le puzzle.

Dans les meilleures traditions des sciences computationnelles, nous serons également paresseux et nous nous demanderons de trouver une fonction qui nous permettrait de nous éloigner des représentations unidimensionnelles des nœuds et d'aller vers des vecteurs de propriété multidimensionnels.

Ici, nous nous familiarisons avec les intégrations de graphiques au sens moderne du terme.

Formellement, nous voulons:

1) Définir un codeur (une fonction de conformité ENC qui définit une transformation de nœud$$ $ en ligne $ u $ en ligne $ en vecteur$$ $ inline $ z_u $ inline $ );
2) Déterminer la fonction de similitude des nœuds (une mesure de proximité dans le graphe, que nous appliquerons à l'entrée de l'encodeur);
3) Optimiser les paramètres de l'encodeur pour que:

$$$$ affichage $$ similitude (u, v) \ environ z_ {v} ^ {T} z_v $$ affichage $$

Nous nous efforçons de veiller à ce que les sommets étroitement espacés dans le graphique reçoivent une représentation proche dans la cartographie vectorielle. Autrement dit, de sorte que l'angle entre les deux vecteurs obtenus soit minimal.

Génial, mais comment la déterminer, cette proximité dans le graphique?

Par exemple, nous supposons que le poids de la nervure est une bonne mesure de proximité et peut être approximativement considéré comme égal au produit scalaire pour les plongements de deux nœuds. La fonction de perte pour ce cas prendra la forme:

$$$$ afficher $$ L = \ sum _ {(u, v) \ en V \ fois V} || z_ {u} ^ {T} z_v - A_ {u, v} || ^ 2, $$ afficher $$

il reste à trouver (par exemple, descente de gradient) la matrice$$ $ inline $ Z \ in \ mathbb {R} ^ {d \ times | V |} $ inline $ ce qui minimise$$ $ en ligne $ L $ en ligne $ .

Une autre approche consiste à déterminer l'environnement.$$ $ en ligne $ N (v) $ en ligne $ car le sommet est plus large que de nombreux voisins.

Cela nous aidera à parcourir le graphique. DeepWalk est le premier projet à utiliser cette approche. L'essence de la méthode est que nous allons démarrer un clochard pour parcourir le graphique au hasard à partir de chaque sommet$$ $ inline $ v $ inline $ , et nourrir de courtes séquences de pics de longueur fixe visités lors de sa promenade dans word2vec.

L'intuition ici est que la distribution de probabilité de visiter les sommets du graphique - une loi de puissance - est très similaire à la distribution de probabilité de l'apparition des mots dans les langues humaines. Et puisque word2vec fonctionne pour les mots, il peut le faire pour les graphiques. Nous l'avons essayé - cela a fonctionné!

Dans DeepWalk, un clochard implémente un processus de Markov de premier ordre - de chaque sommet, nous allons au voisin, selon les probabilités d'une matrice d'adjacence pondérée$$ $ en ligne $ M $ en ligne $ (ou ses dérivés, comme$$ $ en ligne $ M ^ w $ en ligne $ ) Où nous sommes arrivés au sommet n'affecte pas le choix de la prochaine étape.

Pour mettre en œuvre la marche, vous aurez besoin d' un générateur de nombres pseudo-aléatoires et d'un peu d'algèbre . Il est temps d'utiliser le bloc de devis pour sa destination.

«Quiconque est d'accord avec les méthodes arithmétiques de génération, bien sûr, est coupable. Comme cela a été montré à plusieurs reprises, il n’existe pas de nombre aléatoire - il n’existe que des méthodes pour créer de tels nombres, et une procédure arithmétique stricte, bien sûr, n’est pas une telle méthode ... Nous ne traitons que des recettes pour créer des nombres ... "

- John von Neumann

Il reste à conseiller à ceux qui aspirent à une vie juste de trouver l'album "Black and White Noise" à vendre - en 1995, George Marsaglia a écrit sur le CD un tableau d'octets reçus en numérisant le bruit de l'amplificateur pendant la lecture de l'artiste rap et l'a nommé en conséquence.

Le développement de la méthode est node2vec , dans lequel le processus de Markov de second ordre est implémenté - nous regardons d'où il vient, et cela affecte la probabilité de choisir la direction de l'étape suivante. Voyons comment cela fonctionne.

Disons que nous commençons un clochard en marchant autour du graphique à partir du haut$$ $ en ligne $ u $ en ligne $ adjacent au sommet$$ $ inline $ s_1 $ inline $ hauts$$ $ inline $ s_2 $ inline $ et$$ $ en ligne $ w $ en ligne $ - en deux étapes, et$$ $ inline $ s_3 $ inline $ - sur trois. Après chaque étape, nous pouvons effectuer l'une des trois actions possibles: 1) revenir plus près de$$ $ en ligne $ u $ en ligne $ ; 2) explorez les sommets à la même distance de$$ $ en ligne $ u $ en ligne $ , comme celui dans lequel nous sommes maintenant; 3) s'éloigner de$$ $ en ligne $ u $ en ligne $ .

Cette stratégie est mise en œuvre à l'aide de deux paramètres:
$$$ inline $ p $ inline $ - définit la probabilité de revenir au sommet précédent;
$$$ en ligne $ q $ en ligne $ - établit l'équilibre entre la recherche approfondie et la recherche approfondie.

Ces paramètres déterminent les probabilités de transition non normalisées comme suit:

Disons que nous sommes au sommet$$ $ en ligne $ w $ en ligne $ et y est entré par le haut$$ $ inline $ s_1 $ inline $ . Pour les côtes$$ $ inline $ e (w, s_1) $ inline $ nous allons attribuer un poids (probabilité non normalisée)$$ $ en ligne $ 1 / p $ en ligne $ . Pour les côtes$$ $ inline $ e (w, s_2) $ inline $ -$$ $ en ligne $ 1 $ en ligne $ (comme pour toutes les autres arêtes menant à des sommets équidistants de$$ $ en ligne $ u $ en ligne $ ) Pour s'éloigner de$$ $ en ligne $ u $ en ligne $ côtes$$ $ inline $ e (w, s_3) $ inline $ -$$ $ en ligne $ 1 / q $ en ligne $ .

Ensuite, nous normalisons les probabilités (de sorte que la somme soit égale à 1) et passons à l'étape suivante.

Nous sommes intéressés par la séquence des pics visités - nous l'enverrons à word2vec ( cet article vous aidera à y faire face, ou à faire la leçon 8 du cours Deep Learning sur les doigts ). La sélection de stratégies pour le clochard, optimales pour résoudre des problèmes spécifiques est un domaine de recherche active. Par exemple, node2vec, que nous avons examiné, est un champion de la classification des pics (par exemple, la détermination de la toxicité des drogues ou le sexe / âge / race d'un membre d'un réseau social).

Nous allons optimiser la probabilité d'apparition de pics sur le trajet du clochard, la fonction de perte:

$$$$ afficher $$ L = \ sum_ {u \ dans V} \ sum_ {v \ dans N_ {R} (u)} -log (P (v | z_u)) $$ afficher $$

sous sa forme explicite, une charge de calcul assez coûteuse

$$$$ affiche $$ L = \ sum_ {u \ in V} \ sum_ {v \ in N_ {R} (u)} -log (\ frac {e ^ {z_ {u} ^ {T} z_v}} { \ sum_ {n \ in V} e ^ {z_ {u} ^ {T} z_n}}), $$ afficher $$

qui, par un coup de chance, est résolu par un échantillonnage négatif , car

$$$$ affiche le journal $$ (\ frac {e ^ {z_ {u} ^ {T} z_v}} {\ sum_ {n \ in V} e ^ {z_ {u} ^ {T} z_n}}) \ approx log (\ sigma (z_ {u} ^ {T} z_v)) - \ sum_ {i = 1} ^ {k} log (\ sigma (z_ {u} ^ {T} z_ {n_i}))), \\ où \, \, \, n_i \ sim P_V, \ sigma (x) = \ frac {1} {1 + e ^ {- x}}. $$ display $$

Nous avons donc trouvé comment obtenir une représentation vectorielle des sommets. Le truc, c'est le chapeau!

Comment préparer des plongements pour les côtes:

Nous devons définir un opérateur qui permet toute paire de sommets$$ $ en ligne $ u $ en ligne $ et$$ $ inline $ v $ inline $ construire une représentation vectorielle$$ $ en ligne $ z _ {(u, v)} = g (z_u, z_v) $ en ligne $ , qu'ils soient connectés ou non sur le graphique. Un tel opérateur peut être:

a) moyenne arithmétique:$$ $ inline $ [z_u \ oplus z_v] _i = \ frac {z_u (i) + z_v (i)} {2} $ inline $ ;
b) l'œuvre de Hadamard:$$ $ inline $ [z_u \ odot z_v] _i = z_u (i) * z_v (i) $ inline $ ;
c) norme L1 pondérée:$$ $ inline $ || z_u - z_v || _ {\ overline {1} i} = | z_u (i) - z_v (i) | $ inline $ ;
d) taux L2 pondéré:$$ $ inline $ || z_u - z_v || _ {\ overline {2} i} = | z_u (i) - z_v (i) | ^ 2 $ inline $ .

Dans les expériences, le travail de Hadamard se comporte le plus régulièrement.

Juste au cas où, souvenez-vous du théorème du déjeuner gratuit:

Aucun algorithme n'est universel - cela vaut la peine de vérifier plusieurs méthodes.

Le développement de node2vec est le projet OhmNet , qui vous permet de combiner plusieurs graphiques dans une hiérarchie et de construire des incorporations de sommets pour différents niveaux de la hiérarchie. Il a été initialement développé pour modéliser les liaisons entre les protéines dans différents organes (et elles se comportent différemment selon l'emplacement).

Un lecteur avisé verra des similitudes avec la structure organisationnelle et les processus opérationnels.

Et nous - nous reviendrons sur un exemple du domaine du recrutement informatique - la sélection des personnes les plus adaptées à l'équipe déjà existante. Plus tôt, nous avons considéré les graphiques unimodaux des relations des données conditionnelles obtenues à partir de l'histoire de l'interaction (dans le graphique unimodal du sommet et de la connexion - du même type). En réalité, le nombre de cercles sociaux dans lesquels un individu peut être inclus est supérieur à un.

Supposons que, en plus de l'historique de la participation conjointe à des compétitions, nous avons également collecté des informations sur la façon dont les datacenters communiquaient dans notre chat confortable . Maintenant, nous avons déjà deux graphiques de connexions, et OhmNet est parfait pour résoudre le problème de la création de plongements à partir de plusieurs structures.

Maintenant - concernant les lacunes des méthodes basées sur des encodeurs peu profonds - à l'intérieur de word2vec, il n'y a qu'une seule couche cachée, dont les poids codent l'encodage. En sortie, nous obtenons une table de correspondance sommet-vecteur. Toutes ces approches ont les limitations suivantes:

• Chaque sommet est codé par un vecteur unique et le modèle n'implique pas de partage de paramètres;
• Nous ne pouvons encoder que les sommets que le modèle a vu pendant l'entraînement - nous ne pouvons rien faire pour les nouveaux sommets (sauf comment recycler à nouveau l'encodeur);
• Les vecteurs de propriétés de sommet ne sont en aucun cas pris en compte.

Les réseaux convolutionnels graphiques sont exempts des lacunes indiquées. Nous sommes arrivés au Decagon!

Nos journées sont un clochard aléatoire pour tout le monde et tout le monde

À propos des clochards, j'ai eu la chance d'écrire mon premier master et de le défendre en 2003, mais avec une formation approfondie, j'ai dû suivre la voie classique pour comprendre ce qui était sous le capot. Et c'est drôle là-bas.

Voyons d'abord pourquoi les méthodes standard d'apprentissage en profondeur - ne correspondent pas aux graphiques.

Les comptes ne sont pas des chats pour vous!

L'ensemble moderne d'outils d'apprentissage en profondeur (réseaux multicouches, convolutionnels et récurrents) est optimisé pour résoudre des problèmes sur des données assez simples - séquences et réseaux. Un graphique est une structure plus compliquée. L'un des problèmes qui nous empêchera de prendre la matrice d'adjacence et de l'envoyer au réseau neuronal est l' isomorphisme .

Dans notre rubrique jouets$$ $ en ligne $ g $ en ligne $ composé de sommets$$ $ inline $ \ {A, B, C, D \} $ inline $ , pour construire une matrice d'adjacence$$ $ inline $ a $ inline $ , nous avons suggéré une numérotation de bout en bout$$ $ en ligne $ \ {1,2,3,4 \} $ en ligne $ . Il est facile de voir que nous pouvons numéroter les sommets différemment, par exemple$$ $ en ligne $ \ {1,3,2,4 \} $ en ligne $ , ou$$ $ en ligne $ \ {4,1,3,2 \} $ en ligne $ - recevoir à chaque fois une nouvelle matrice d'adjacence du même graphe.

$$$ inline $ \ begin {align *} A = \ left [\ begin {matrix} 0 & 1 & 3 & 0 \\ 1 & 0 & 2 & 1 \\ 3 & 2 & 0 & 0 \\ 0 & 1 & 0 & 0 \ end {matrix} \ right], \, A ^ {\ {1,3,2,4 \}} = \ left [\ begin {matrix} 0 & 3 & 1 & 0 \\ 3 & 0 & 2 & 0 \\ 1 & 2 & 0 & 1 \\ 0 & 0 & 1 & 0 \ end {matrix} \ right], \, A ^ {\ {4,1,3,2 \}} = \ left [\ begin {matrix} 0 & 1 & 2 & 1 \\ 1 & 0 & 0 & 0 \\ 2 & 0 & 0 & 3 \\ 1 & 0 & 3 & 0 \ end {matrix} \ right]. \ end {align *} $ inline $

Dans le cas des scellés, notre réseau devrait apprendre à les reconnaître pour toutes les permutations possibles de lignes et de colonnes - c'est un autre problème. Comme exercice, essayez de changer la numérotation des points dans l'image ci-dessous afin que lorsque vous les connectez en série, vous obtenez un chat.

Le problème suivant pour les graphiques avec des réseaux de neurones ordinaires est la dimension d'entrée standard. Lorsque nous travaillons avec des images, nous normalisons toujours la taille de l'image afin de l'envoyer à l'entrée réseau - c'est une taille fixe. Ces graphiques ne fonctionneront pas avec les graphiques - le nombre de sommets peut être arbitraire - presser la matrice de connectivité à une dimension donnée sans perdre d'informations est un autre défi.

Solution - nous allons construire de nouvelles architectures, inspirées de la structure des graphes.

Pour ce faire, nous utilisons une stratégie simple en deux étapes:

1. Pour chaque sommet, nous construisons un graphe de calcul en utilisant un clochard;
2. Nous collectons et transformons des informations sur les voisins.

Rappelons que nous stockons les propriétés des sommets dans des vecteurs$$ $ inline $ f ^ {(u)} $ inline $ - colonnes matricielles$$ $ inline $ X \ in \ mathbb {R} ^ {k \ times | V |} $ inline $ et notre tâche est pour chaque sommet$$ $ en ligne $ u $ en ligne $ collecter les propriétés des sommets voisins$$ $ inline $ f ^ {(v \ in N (u))} $ inline $ pour obtenir des vecteurs d'intégration$$ $ inline $ z_ {u} $ inline $ . Un graphe de calcul peut avoir une profondeur arbitraire. Considérez une option à deux couches.

La couche zéro correspond aux propriétés des sommets, la première est une agrégation intermédiaire utilisant une fonction (indiquée par un point d'interrogation), la seconde est l'agrégation finale, qui produit les vecteurs d'intégration qui nous intéressent.

Et qu'y a-t-il dans les boîtes?

Dans le cas simple , une couche de neurones et de non-linéarité:

$$$$ afficher $$ h ^ 0_v = x_v (= f ^ {(v)}); \\ h ^ k_v = \ sigma (W_k \ sum_ {u \ in N (v)} \ frac {h ^ {k-1} _v} {| N (v) |} + B_k h ^ {k-1} _v), \ forall k \ in \ {1, ..., K \}; \\ z_v = h ^ K_v, $$ display $$

où$$ $ inline $ W_k $ inline $ et$$ $ inline $ B_k $ inline $ - les poids du modèle que nous apprendrons par descente de gradient, en appliquant l'une des fonctions de perte considérées, et$$ $ inline $ \ sigma $ inline $ - non linéarité, par exemple RELU:$$ $ inline $ \ sigma (x) = max (0, x) $ inline $ .

Et ici, nous nous trouvons à la croisée des chemins - selon la tâche à accomplir, nous pouvons:

• d'étudier sans professeur et de profiter de l'une des fonctions de perte considérées précédemment - les clochards ou le poids des bords. Les poids résultants seront optimisés de sorte que les vecteurs de sommets similaires soient placés de manière compacte;
• commencer une formation avec un enseignant, par exemple, pour résoudre le problème de classification, en se demandant si le médicament sera toxique.

Pour le problème de classification binaire, la fonction de perte prend la forme:

$$$$ afficher $$ L = \ sum_ {v \ in V} log y_v (\ sigma (z_v ^ T \ theta)) + (1-y_v) log (1- \ sigma (z_v ^ T \ theta)), $ $ afficher $$

où$$ $ inline $ y_v $ inline $ - classe vertex$$ $ inline $ v $ inline $ ,$$ $ inline $ \ theta $ inline $ Est le vecteur des poids, et$$ $ inline $ \ sigma $ inline $ - non linéarité, par exemple un sigmoïde:$$ $ inline $ \ sigma (x) = \ frac {1} {1 + e ^ {- x}} $ inline $ .

Ici, un lecteur formé reconnaîtra l'entropie croisée et la régression logistique, tandis qu'un lecteur non préparé envisagera de suivre un cours d'apprentissage automatique pour se sentir à l'aise avec la tâche de classification , des algorithmes simples et plus avancés pour la résoudre (y compris le renforcement du gradient ).

Et nous allons continuer et examiner comment GraphSAGE , le signe avant-coureur de Decagon, fonctionne.

Pour chaque sommet$$ $ inline $ v $ inline $ nous regrouperons les informations des voisins$$ $ inline $ u \ in N (v) $ inline $ et elle-même.

$$$$ afficher $$ h ^ k_v = \ sigma ([W_k \ cdot AGG (\ {h ^ {k-1} _u, \ forall u \ in N (v) \}), B_k h ^ {k-1} _v]), $$ afficher $$

où$$ $ inline $ AGG $ inline $ - une désignation généralisée de la fonction d'agrégation - le plus important - différenciable.

Moyennage: prendre une moyenne pondérée des voisins

$$$$ afficher $$ AGG = \ sum_ {u \ dans N (v)} \ frac {h ^ {k-1} _u} {| N (v) |}. $$ afficher $$

Mise en commun: valeur moyenne / maximale par élément

$$$$ afficher $$ AGG = \ gamma (\ {Qh ^ {k-1} _u, \ forall u \ in N (v) \}). $$ afficher $$

LSTM: Secouez l'environnement (ne mélangez pas!) Et exécutez en LSTM

$$$$ afficher $$ AGG = LSTM ([h ^ {k-1} _u, \ forall u \ in \ pi (N (v))]). $$ afficher $$

Pinterest, , PinSAGE .

LSTM ( ). IT-.

:

• : , — , .
• , : / , — .

, — . , . , , , . (/) , , , — — , 30 .

.

— (multi-label node
classification task) — . — . () ( — — 42% ). GraphSAGE, , — .

!

, — , , . , .

- , Decagon. , -, -, , -, — ri . . - 964 ( ) .

— , -, -.

,

$$

$$h^k_v = \sigma(\sum_rW^{k-1}_r(\sum_{u \in N_r(v)} \frac{h^{k-1}_u}{\sqrt{|N_r(v)||N_r(u)|}}+\frac{h^{k-1}_v}{|N_r(v)|})),$$

$$$\sigma$— , RELU. , Decagon — . , , GraphSAGE. , .

, .

— , . -. $$$(u,r,v)$, :

$$$\begin{align*}g(u,r,v) = \left\{ \begin{matrix} z^T_uD_{r_i}RD_{r_i}z_j & u,v - ; \\ z^T_uM_rz_v & u,v - \, \, , \,\, \, . \end{matrix} \right.\end{align*}$

, :

$$

$$p^{uv}_{r} = p((u,r,v) \in E) = \sigma (g(u, r, v)), \sigma(x) = \frac{1}{1 + e^{-x}}.$$

, (end-to-end) -, : (i) $$$W_r$— , (ii) $$$M_r$— - -, (iii) $$$R$— , (iv) $$$D_{r_i}$— .

— - .

— .

— , , : 1) — — ; 2) " , , , " — - . , , , .

— — .

, ( ) , . , , GenBank 1 , , - — , . — , - ( ) , SNAP .

.

Neo4j , (property graph).

, . , , — (i) -, (ii) , (iii) , — — . .

— :

De plus, la contribution de Neo4j à l'industrie est de créer le langage Cypher déclaratif , qui implémente un modèle de graphique avec des propriétés et fonctionne sous la forme similaire à SQL avec les types de données suivants: sommets, relations, dictionnaires, listes, entiers, virgule flottante et nombres binaires, et cordes. Un exemple de requête qui renvoie une liste de films mettant en vedette Nicole Kidman:

MATCH (nicole:Actor {name: 'Nicole Kidman'})-[:ACTED_IN]->(movie:Movie) WHERE movie.year < $yearParameter RETURN movie 

À l'aide de béquilles, Neo4j peut fonctionner en mémoire.

Il convient également de mentionner Gephi - un outil pratique pour visualiser et disposer des graphiques sur un plan - le premier outil d'analyse de réseau testé personnellement. Avec un étirement, nous pouvons supposer que dans Gephi, il est possible d'implémenter un graphique avec les propriétés des sommets et des bords, bien que travailler avec lui ne soit pas très pratique, et l'ensemble des algorithmes d'analyse est limité. Cela ne porte pas atteinte aux mérites du package - pour moi, il est en première place parmi les outils de visualisation. En maîtrisant le format de stockage interne GEXF , vous pouvez créer des images impressionnantes. Il attire la possibilité d'exporter facilement sur le Web, ainsi que la possibilité de définir les propriétés des sommets et des bords dans le temps et d'obtenir des animations complexes en conséquence - il a construit les itinéraires pour les vendeurs à partir des données de vente. Tout cela grâce à la disposition des graphiques sur la carte par les coordonnées des sommets - la partie standard du package.

Maintenant, je mène la plupart des recherches analytiquement, je dessine des images à la fin.

Ma recherche d'outils et de méthodes de traitement des données dans des systèmes complexes connectés se poursuit. Il y a trois ans, j'ai trouvé une solution pour travailler avec des graphes multimodaux. La bibliothèque SNAP de Jure Leskovek est un outil qu'il a développé pour lui-même et qui a déjà mesuré beaucoup de choses. J'utilise Snap.py - la version pour Python (fonctions proxy vers SNAP implémentées en C ++) et un ensemble d'environ trois cents opérations disponibles me suffit dans la plupart des cas.

Récemment, Marinka Zhitnik a publié MAMBO - un ensemble d'outils (à l'intérieur - SNAP) pour travailler avec des réseaux multimodaux et un tutoriel sous la forme d'une série de cahiers Jupyter avec une analyse exemplaire des mutations génétiques.

Enfin, il y a le graphique SAP HANA - à l'intérieur de ML, SQL, OpenCypher - tout ce que votre cœur désire.

En faveur de SAP HANA, le fait que creuser soit susceptible d'entraîner des données de transaction bien structurées de l'ERP, alors que les données pures valent beaucoup. Un autre avantage - des outils puissants pour trouver des sous-graphiques par des modèles donnés - une tâche utile et difficile, dont la mise en œuvre dans d'autres packages ne s'est pas rencontrée et n'a pas utilisé de programmes spécialisés . Une licence gratuite pour le développeur fournit une base de données de 1 Go - juste assez pour jouer avec des réseaux assez grands. Un appel drôle - un ensemble d'algorithmes analytiques prêts à l'emploi - est petit, le PageRank devra être implémenté de manière indépendante. Pour ce faire, vous devez maîtriser GraphScript , un nouveau langage de programmation, mais ce sont des choses triviales . Comme l'a dit mon entraîneur de slalom d'aviron, pour le maître - c'est de la poussière!

Maintenant, où trouver les données pour en construire des graphiques. Quelques idées:

• Dépôts publics universitaires: Stanford - General and Biomedical , Colorado ;
• Combiner le plan de projet avec la structure organisationnelle et le registre des risques;
• Identifier la relation entre la structure du produit, la technologie et les souhaits des utilisateurs;
• Mener une étude sociographique en équipe;
• Trouvez quelque chose de vous-même, inspiré par les projets de cours cs224w de l'année dernière .

De quoi avoir peur

On peut dire que ce sera le dernier avertissement sur les risques associés à ce parti.

Comme vous le savez, mesdames et messieurs, l'objectif du programme est de refléter la situation à l'avant-garde d'un groupe de recherche très productif et généreusement financé. C'est comme Leningrad , seulement sur les mathématiques modernes. Effets secondaires possibles:

1. Dunning-Krueger , modifié, sans l'euphorie d'un novice et plateau d'excellence. Leskovek essaie de rattraper son retard.
2. Ennui dans une province au bord de la mer. Sur les 400 personnes du cours qui ont reçu l'appareil, elles m'ont fait écrire un projet et réussir l'examen de la première session de mon deuxième master, les décomptes sont allés un an et demi. Les enseignants dans leurs activités de recherche sont restés au niveau des mesures de modularité et de centralité. Sur mitaps sur python et les données est également triste. En général, si vous ne savez pas vous divertir, je vous ai prévenu.
3. Fierté d'un accent slave dans la langue anglaise.

Mémo de lecture

Salut, reproducteur!

Dans l'aventure que Jura Leskovek nous a donnée, vous avez besoin de temps libre. Le cours se compose de 20 conférences, quatre devoirs, dont chacun est recommandé d'allouer environ 20 heures, de la littérature recommandée, ainsi qu'une longue liste de documents supplémentaires qui permettront de faire une première impression de la situation à la pointe des progrès dans l'un des sujets abordés.

Pour effectuer les tâches, il est fortement recommandé d'utiliser la bibliothèque SNAP (dans un sens, l'ensemble du cours peut être considéré comme un aperçu de ses capacités).

De plus, vous pouvez essayer de mettre en œuvre votre propre projet ou écrire un tutoriel sur un sujet que vous aimez.

Je pense qu'après une immersion dans la théorie des graphes, les questions sur les arbres ne seront plus effrayantes. Cependant, ce n'est que l'avis d'un amateur qui n'a jamais de sa vie pris la position d'un développeur qui n'a pas été interviewé.