🤱🏻 🔳 👩‍🚒 Programmation dynamique dans les problèmes d'olympiades 🙎🏿 👨🏼‍⚕️ 🥩

Salut

Récemment, j'ai résolu des problèmes dans les archives de Timus Online Judge et suis tombé sur une section appelée tâches de programmation dynamique . Ce type de tâche m'intéresse particulièrement, car souvent cette approche assure la rapidité et l'élégance de la solution. Qu'est-ce que la programmation dynamique?

La programmation dynamique est une approche de résolution de problèmes dans laquelle il existe une division en sous-tâches plus «simples» par rapport à l'original. Le mot "dynamique" a un sens proche de "inductif": on suppose que la réponse est connue pour un certain sens

k

$k$ , et je veux trouver la réponse pour

k + 1

$k + 1$ . En mathématiques, cela s'appelle une transition inductive, et c'est l'idée principale de la programmation dynamique.

Exemples simples

La tâche la plus frappante et la plus indicative est la tâche de calculer

n

$n$ numéro de la séquence de Fibonacci. Il est connu que la séquence a les propriétés suivantes:

F_{0} = F_{1} = 1, F_{n} = F_{n - 1} + F_{n - 2} .

$F_0 = F_1 = 1, \ F_n = F_ {n-1} + F_ {n-2}.$

Cela implique immédiatement la formule de récurrence:

int Fibonacci(int n) { if(n == 1 || n == 2) return 1; return Fibonacci(n-1) + Fibonacci(n-2); }

Si la récursivité recherche un nombre "à partir de la fin", la méthode suivante calcule séquentiellement tous les nombres situés entre

0

$0$ et

n

$n$ :

 int dpFibonacci(int n) { int prev1 = 1; int prev2 = 1; int curr = 0; for(int j = 2; j < n; j++) { curr = prev1 + prev2; prev1 = prev2; prev2 = curr; } return curr; }

Il est clair que pour des

n

$n$ cet algorithme fonctionne beaucoup plus rapidement: il ne calcule pas plusieurs fois les valeurs intermédiaires. Prenons un exemple un peu plus complexe.

Exemple 1. Vous marchez sur un escalier à péage. Pour marcher

i

$i$ étape que vous devez payer

a_{i}

$a_i$ pièces de monnaie. Vous pouvez passer à l'étape suivante ou en sauter une. Tâche: passer

n

$n$ étapes et dépenser le moins de pièces possible.

Il est clair qu'en franchissant chaque étape, nous minimisons le nombre de «paiements», mais nous pouvons entrer dans une étape très coûteuse, que nous voudrions éviter. Créer un tableau de valeurs

d

$d$ dans lequel

j

$j$ -le lieu sera le nombre (minimum) de pièces qui doivent être dépensées pour

j

$j$ e étape. Il est immédiatement clair que

d_{1} = a_{1}, d_{2} = a_{2}

$d_1 = a_1, \ d_2 = a_2$ . Et puis nous prendrons un minimum des deux étapes précédentes et ajouterons le coût de l'étape elle-même:

d_{i} = m i n g a u c h e (d_{i - 1}, d_{i - 2} d r o i t e) + a_{i} .

$d_i = \ min \ gauche (d_ {i-1}, d_ {i-2} \ droite) + a_ {i}.$

Nous modifions un peu les conditions du problème: supposons qu'à certaines étapes vous pouvez obtenir des pièces (cela signifie que

a_{k} < 0

$a_k <0$ ) Que faut-il changer dans l'algorithme pour qu'il donne le bon résultat?

Solution

Il suffit de changer le «début» de notre dynamique. Si le premier escalier ne nous apporte pas de pièces, il est conseillé de sauter par-dessus, cependant, si

a_{1} < 0

$a_1 <0$ , il vaut mieux marcher et récupérer vos pièces. Alors

d_{2} = m i n g a u c h e (0, d_{1} d r o i t e) + a_{2}

$d_2 = \ min \ gauche (0, d_1 \ droite) + a_2$ .

Prenons un autre exemple qui utilise une dynamique «bidimensionnelle».

Exemple 2. Dans le labyrinthe, il y a

n f o i s m

$n \ fois m$ chambres, dont chacune contient de l'or (dans une cage

(i, j)

$(i, j)$ mensonges

a_{i j}

$a_ {ij}$ or). La tâche consiste à déterminer quelle quantité maximale d'or peut être collectée avec un itinéraire optimal à partir d'un point

(0, 0)

$(0,0)$ au point

(n, m)

$(n, m)$ si vous pouvez descendre ou à droite.

Donc, nous voulons connaître le meilleur itinéraire vers la cellule

(i, j)

$(i, j)$ . Nous pouvons arriver ici à partir de deux cellules -

(i - 1, j)

$(i-1, j)$ et

(i, j - 1)

$(i, j-1)$ . Étant donné que les routes optimales pour ces deux cellules sont connues (elles sont stockées dans un tableau

d

$d$ ), puis la réponse pour la cellule

(i, j)

$(i, j)$ obtenu comme suit:

d_{i j} = m a x l e f t (d_{i - 1 j}, d_{i j - 1} r i g h t) + a_{i j} .

$d_ {ij} = \ max \ left (d_ {i-1j}, d_ {ij-1} \ right) + a_ {ij}.$

Il s'agit d'une autre tâche de programmation dynamique classique, dont les modifications sont assez courantes dans les tâches de programmation sportive. Une tâche similaire est expliquée plus en détail ici .

Tâches plus difficiles

Si vous le souhaitez, une approche dynamique peut être vissée où vous le souhaitez. Considérez une tâche des archives du juge en ligne Timus.

La formulation mathématique du problème est la suivante: il faut trouver le nombre minimum de termes nécessaires pour décomposer un nombre donné en carrés entiers.

Comme précédemment, supposons que nous connaissions les réponses pour tous les nombres

k - 1

$k-1$ qui sont stockés dans un tableau

d

$d$ et nous aimerions trouver

d_{k}

$d_ {k}$ .

Prenez ce numéro

k

$k$ et analyser quelles situations peuvent être:

$k$ est un carré plein. Dans ce cas $d_ {k} = 1$ .
Peut-être le numéro précédent $k-1$ était un carré complet. Alors $d_ {k} = d_ {k-1} + 1$ .

En général, l'option d'ajouter une unité à la précédente ne semble pas si mauvaise.

On procède comme suit: on cherche une décomposition

k = q^{2} + s

$k = q ^ 2 + s$ tel que

d_{q^{2}} + d_{s} < d_{k - 1} + 1.

$d_ {q ^ 2} + d_s <d_ {k-1} + 1.$

Depuis

q^{2}

$q ^ 2$ - plein carré alors

d_{q^{2}} = 1

$d_ {q ^ 2} = 1$ et

d_{s} < d_{k - 1},

$d_s <d_ {k-1},$

c'est-à-dire que nous avons trouvé une partition qui est simplement meilleure que

d_{k - 1} + 1

$d_ {k-1} + 1$ , et la réponse dans ce cas sera

d_{k} = d_{s} + d_{q^{2}} = d_{s} + 1.

$d_k = d_ {s} + d_ {q ^ 2} = d_s + 1.$

Exemple de code Java qui implémente cet algorithme:

 for(int k = 1; k <= n; k++) { int best = d[k - 1] + 1; //      int q = 1; while(k - q*q >= 0) { // k = q*q + s if(k - q*q == 0) { // k -   best = 1; break; } else if(d[k - q*q] < best) best = d[k - q*q] + 1; q++; } d[k] = best; }

Considérez le problème suivant. L'objectif est de construire un escalier à partir de

N

$N$ cubes selon les règles:

l'escalier a au moins deux marches;
un escalier ne peut pas avoir deux marches identiques;
les marches de l'escalier vont dans l'ordre croissant (c'est-à-dire que le suivant est plus grand que le précédent).

Cette fois, nous allons construire une dynamique bidimensionnelle. Créer une table

d

$d$ dans lequel la position

(i, j)

$(i, j)$ le nombre d'escaliers composé de

i

$i$ cubes dont la hauteur ne dépasse pas

j

$j$ . Si cela fonctionne, alors la réponse à notre problème sera la somme

s u m l i m i t s_{j = 1}^{n} d_{n j} .

$\ sum \ limits_ {j = 1} ^ n d_ {nj}.$

Donc, nous allons résoudre le problème de trouver le nombre d'escaliers composé de

i

$i$ cubes qui sont grands

j

$j$ . La photo montre les escaliers qui tombent dans

d_{74}

$d_ {74}$ :

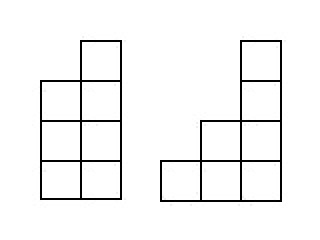
Puisque nous connaissons tous les escaliers, qui se composent de moins de cubes, nous allons «diviser» les escaliers

(i, j)

$(i, j)$ colonne de droite. Le résultat est un escalier c

i - j

$i-j$ cubes. Exemple pour

i = 9, j = 4

$i = 9, \ j = 4$ :

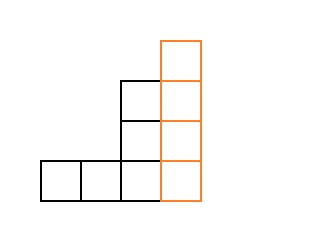
Mais pour de tels escaliers, le résultat est déjà connu, nous allons donc trier tous ces escaliers avec un cycle

k

$k$ et additionnez tous les résultats. De cette façon

d_{i j} = s u m l i m i t s_{k = 1}^{j - 1} d_{i - j k} .

$d_ {ij} = \ sum \ limits_ {k = 1} ^ {j-1} d_ {i-jk}.$

Maintenant, nous allons trier les hauteurs des escaliers:

d_{i j} = s u m l i m i t s_{k = 1}^{j - 1} d_{i - j k}, j = o v e r l i n e 1, i .

$d_ {ij} = \ sum \ limits_ {k = 1} ^ {j-1} d_ {i-jk}, \ j = \ overline {1, i}.$

Enfin, changer

i

$i$ de

1

$1$ avant

n

$n$ nous obtenons la réponse.

Important : dans le processus de construction de notre matrice, il est nécessaire de prendre en compte

d_{i i} = 1

$d_ {ii} = 1$ , car sinon, certains types d'escaliers seront "perdus" (lorsqu'ils seront "séparés"), mais il va sans dire qu'un tel escalier ne satisfait pas aux conditions du problème, la réponse sera donc le nombre

d_{n n} - 1

$d_ {nn} - 1$ .

Exemple de code Java qui implémente cet algorithme:

 dp = new long[n + 1][n+1]; d[1][1] = 1; d[2][1] = 0; d[2][2] = 1; for(int i = 3; i < n + 1; i++) { for(int j = 2; j <i; j++) { long cnt = 0; for(int k = 1; k < j; k++) { cnt += d[i - j][k]; } d[i][j] = cnt; } d[i][i] = 1; //    } long answer = 0L; for(int i = 0; i <= n; i++) { answer += d[n][i]; } answer--; //

La tâche suivante est résolue à l'aide d'un tableau unidimensionnel.

Alors ce que nous avons. Le premier ent connaît 2 mots. Chaque ent enseigne tous les mots qu'il connaît lui-même deux ents: jeunes et vieux. À leur tour, les jeunes ont appris autant de mots qu'il le sait déjà, et les vieux n'ont appris qu'un seul mot. Vous devez savoir combien d'Ents savent exactement

K

$K$ mots (il faut déduire le nombre de ces ents modulo

P

$P$ )

La solution est assez simple. Créer un tableau

d

$d$ dans lequel

i

$i$ -th place, nous allons stocker le nombre d'ents (modulo

P

$P$ ) qui sait

i

$i$ des mots. Tout commence par le premier ent, qui connaît deux mots, donc

d_{2} = 1

$d_2 = 1$ . Et puis tout est simple:

Tous les élèves qui connaissent un nombre impair de mots sont anciens et ne peuvent apprendre que des précédents. Par conséquent, pour impair $i: \ d_i = d_ {i-1};$
Quant aux ents qui connaissent un nombre pair de mots, ce sont tous ceux qui ont reçu le même nombre de mots des elfes (jeunes) $+$ ceux qui ont appris de la précédente (ancienne); c'est-à-dire, même $i$ nous avons $d_i = d _ {{i \ backslash 2}} + d_ {i-1}$ .

Reste à traiter du calcul modulo. Afin de ne pas stocker de nombres énormes, nous retiendrons immédiatement toutes les valeurs modulo.

Exemple de code Java qui implémente cet algorithme:

 int[] d = new int[K + 1]; if(K >= 2) d[2] = 1; if(P != 1) { for(int i = 3; i <= K; i++) { if(i % 2 != 0) { d[i] = d[i - 1]; } else { d[i] = ((d[i/2] % P) + d[i - 1] % P) % P; } } } else d[K] = 0;

Ressources utilisées:

Juge en ligne Timus;
Un peu sur la programmation dynamique;
Propriétés de comparaison modulo.

Programmation dynamique dans les problèmes d'olympiades

Exemples simples

Tâches plus difficiles

More articles: