Présentation
L'équation de type elliptique la plus courante est l'équation de Poisson.
De nombreux problèmes de physique mathématique se réduisent à la solution de cette équation, par exemple les problèmes de distribution stationnaire de la température dans un solide, les problèmes de diffusion, les problèmes de distribution du champ électrostatique dans un milieu non conducteur en présence de charges électriques, et bien d'autres.
Pour résoudre des équations elliptiques dans le cas de plusieurs mesures, des méthodes numériques sont utilisées pour convertir des équations différentielles ou leurs systèmes en systèmes d'équations algébriques. La précision de la solution est déterminée par le pas de la grille de coordonnées, le nombre d'itérations et la grille de bits de l'ordinateur [1]
Le but de la publication est d'obtenir une solution à l'équation de Poisson pour les conditions aux limites de Dirichlet et Neumann, d'étudier la convergence de la méthode de relaxation de la solution à l'aide d'exemples.
L'équation de Poisson fait référence à des équations de type elliptique et dans le cas unidimensionnel a la forme [1]:
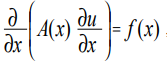
(1)
où x est la coordonnée; u (x) est la fonction souhaitée; A (x), f (x) sont des fonctions de coordonnées continues.
Nous résolvons l'équation de Poisson unidimensionnelle pour le cas A = 1, qui dans ce cas prend la forme:
(2)
Sur l'intervalle [xmin, xmax] on définit une grille de coordonnées uniforme avec un pas Δ:
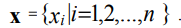
(3)
Les conditions aux limites du premier type (conditions de Dirichlet) pour le problème considéré peuvent être représentées comme:
(4)
où x1, xn sont les coordonnées des points limites de la région [xmin, xmax]; g1, g2 - certains
constantes.
Les conditions aux limites du second type (conditions de Neumann) pour le problème considéré peuvent être représentées comme:
(5)
En discrétisant les conditions aux limites de Dirichlet sur une grille de coordonnées uniformes (3) en utilisant la méthode des différences finies, on obtient:
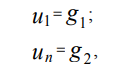
(6)
où u1, un sont les valeurs de la fonction u (x) aux points x1, xn, respectivement.
En discrétisant les conditions aux limites de Neumann sur la grille (3), on obtient:
(7)
Équation discrétisante (2) pour les points de grille internes, on obtient:
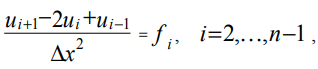
(8)
où ui, fi sont les valeurs des fonctions u (x), f (x) au point de grille avec la coordonnée xi.
Ainsi, à la suite de la discrétisation, nous obtenons un système d'équations algébriques linéaires de dimension n contenant n - 2 équations de la forme (8) pour les points internes de la région et les équations (6) et (7) pour deux points limites [1].
Ce qui suit est une liste Python d'une solution numérique à l'équation (2) avec les conditions aux limites (4) - (5) sur la grille (3).
Solution de référencementfrom numpy import* from numpy.linalg import solve import matplotlib.pyplot as plt x0=0
Nous obtenons:
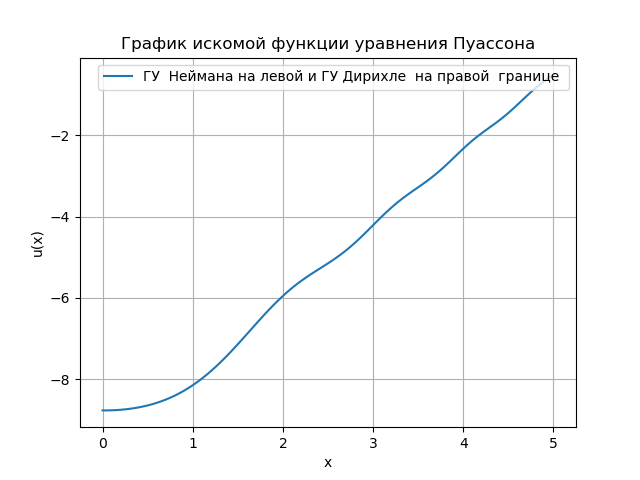
Le programme que j'ai développé en Python est pratique pour analyser les conditions aux limites. L'algorithme de solution ci-dessus en Python utilise la fonction Numpy - u = linalg.solve (a, bT) .T pour résoudre le système d'équations algébriques, ce qui augmente la vitesse avec la matrice carrée {a}. Cependant, avec une augmentation du nombre de mesures, il est nécessaire de passer à l'utilisation de trois matrices diagonales, dont la solution est compliquée même pour une tâche très simple, j'ai trouvé un exemple sur le forum:
Exemple de solution à trois matrices diagonales from __future__ import print_function from __future__ import division import numpy as np import time ti = time.clock() m = 1000 A = np.zeros((m, m)) B = np.zeros((m, 1)) A[0, 0] = 1 A[0, 1] = 2 B[0, 0] = 1 for i in range(1, m-1): A[i, i-1] = 7 A[i, i] = 8 A[i, i+1] = 9 B[i, 0] = 2 A[m-1, m-2] = 3 A[m-1, m-1] = 4 B[m-1, 0] = 3 print('A \n', A) print('B \n', B) x = np.linalg.solve(A, B)
Le programme de solution numérique sur l'uniforme dans chaque direction du problème de Dirichlet de la grille pour l'équation convection-diffusion
[2]
(9)
Nous utilisons des approximations par différences centrales pour le terme convectif et une méthode de relaxation itérative. Pour la dépendance du taux de convergence sur le paramètre de relaxation pour la solution numérique du problème avec f (x) = 1 et 6 (x) = 0.10. Dans la tâche de grille:
(10)
Nous représentons la matrice A comme la somme des matrices diagonales, triangulaires inférieures et triangulaires supérieures:
(10)
La méthode de relaxation correspond à l'utilisation de la méthode itérative :
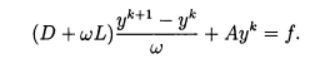
(11)
À
\ parler de relaxation supérieure, quand
- sur la relaxation inférieure.
Liste des programmes from numpy import * """ - . .""" def relaxation(b, f, I1, I2, n1, n2, omega, tol = 1.e-8): h1 = I1 / n1 h2 = I2 / n2 d = 2. / h1**2 + 2. / h2**2 y = zeros([n1+1, n2+1]) ff = zeros([n1+1, n2+1]) bb = zeros([n1+1, n2+1]) for j in arange(1,n2,1): for i in arange(1,n1,1): ff [i,j] = f(i*h1, j*h2) bb[i,j] = b(i*h1, j*h2)
)
Nous obtenons:
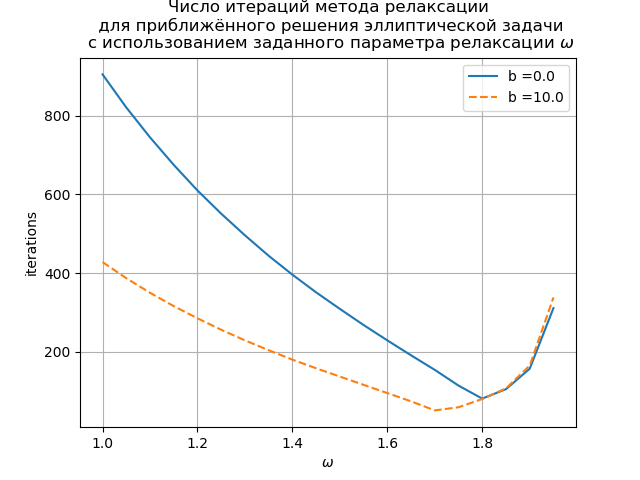
Le graphique montre la dépendance du nombre d'itérations sur le paramètre de relaxation pour l'équation de Poisson (b (x) = 0) et l'équation de convection-diffusion (b (x) = 10). Pour l'équation de la grille de Poisson, la valeur optimale du paramètre de relaxation est trouvée analytiquement et la méthode itérative converge à
.
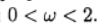
Conclusions:
- La solution du problème elliptique en Python avec un système flexible pour définir les conditions aux limites
- Il est démontré que la méthode de relaxation a une plage optimale ( 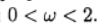) paramètre de relaxation.
Références:
- Ryndin E.A. Méthodes pour résoudre des problèmes de physique mathématique. - Taganrog:
Maison d'édition de TRTU, 2003 .-- 120 p. - Vabishchevich P.N.Méthodes numériques: atelier de calcul. - M .: Maison du livre
Librocom, 2010. - 320 p.