Modélisation de la surface de l'eau à l'aide de FFT et du processeur NeuroMatrix DSP

La transformée de Fourier rapide bien connue a longtemps été utilisée non seulement pour résoudre des problèmes de traitement numérique du signal, de reconnaissance d'objets dans l'image, mais aussi en infographie. Jerry Tessendorf a décrit un modèle mathématique qui vous permet de synthétiser les vagues océaniques et de les animer en temps réel. Ce modèle est basé sur une FFT bidimensionnelle.

Lorsque j'ai été chargé de développer une application pour un processeur DSP qui visualise le fonctionnement d'une FFT, j'ai réalisé que la modélisation des vagues est parfaite à cet effet.

Modèle mathématique de la vague

L'idée de base d'un modèle mathématique d'une onde peut être décrite par l'expression:
$$$\ mathbf H$ = FFT2D ( $$$\ mathbf {\ widetilde H}$ ), FFT2D est désigné comme l'opérateur d'une FFT bidimensionnelle.

$$$\ mathbf H$ Est le champ des hauteurs de la surface de l'eau (taille de la matrice $$$n_1 x n_2$ où $$$n_1$ et $$$n_2$ peut prendre des valeurs de pouvoirs de deux). Les éléments de cette matrice sont les hauteurs des vagues.

$$$\ mathbf {\ widetilde H}$ - signal (taille de la matrice $$$n_1 x n_2$ ), généré selon une certaine loi et en fonction du temps.

$$$\ mathbf {\ widetilde H} = \ mathbf {\ widetilde H_0}. * \ mathbf A + \ overline {\ mathbf {\ widetilde H_0}}. * \ overline {\ mathbf A}$ où les éléments de la matrice $$$\ mathbf A$ c'est$$ $ inline $ e ^ {iω_ {ij} t} = cos⁡ (ω_ {ij} t) + isin (ω_ {ij} t) $ inline $ et la matrice $$$\ overline {\ mathbf A}$ - conjugué complexe à $$$\ mathbf A$ matrice $$$i = 0,1, ... n_1, j = 0,1, ... n_2$

$$$ω_ {ij}$ Sont des éléments matriciels $$$\ Large {\ mathbf ω}$ .

$$$. *$ - multiplication matricielle élément par élément.

$$$\ mathbf {\ widetilde H_0}$ - champ de hauteurs au moment initial t = 0.

$$$\ overline {\ mathbf {\ widetilde H_0}}$ - conjugué complexe à $$$\ mathbf {\ widetilde H_0}$ matrice (taille $$$n_1 x n_2$ )

Pour créer une animation du mouvement des vagues en temps réel, il faut recalculer la matrice $$$\ mathbf {\ widetilde H}$ et $$$\ mathbf H$ changer t . Matrices $$$\ mathbf {\ widetilde H_0}$ , $$$\ overline {\ mathbf {\ widetilde H_0}}$ et $$$\ Large {\ mathbf ω}$ sont calculés une fois et réutilisés.

Passons maintenant à la description du processeur DSP qui, sur la base des formules ci-dessus, doit pouvoir:

1. Calculez FFT.
2. Multipliez les matrices élément par élément.
3. Ajoutez des matrices.
4. Calculez le vecteur des sinus et des cosinus.

En tant que processeur DSP, 1879VM6Ya a été utilisé sur la base de l'architecture NeuroMatrix, développée par le Centre Scientifique et Technique "Module" CJSC. Le circuit de la figure 1.

Le processeur contient 2 cœurs de fonctionnement parallèles NMPU0 et NMPU1 (fonctionnant à une fréquence de 500 MHz), chacun ayant un processeur RISC et un coprocesseur vectoriel (NMCore FPU pour virgule flottante et NMCore INT pour arithmétique entière). Le cœur NMPU0 est destiné au traitement des données à virgule flottante, et NMPU1 est destiné aux données entières. NMPU0 possède 8 banques de mémoire SRAM interne (128 Ko chacune) et NMPU1 possède 4 banques (128 Ko) de la même mémoire. Sur 1879VM6Ya, un contrôleur DMA et une interface DDR2 sont installés.



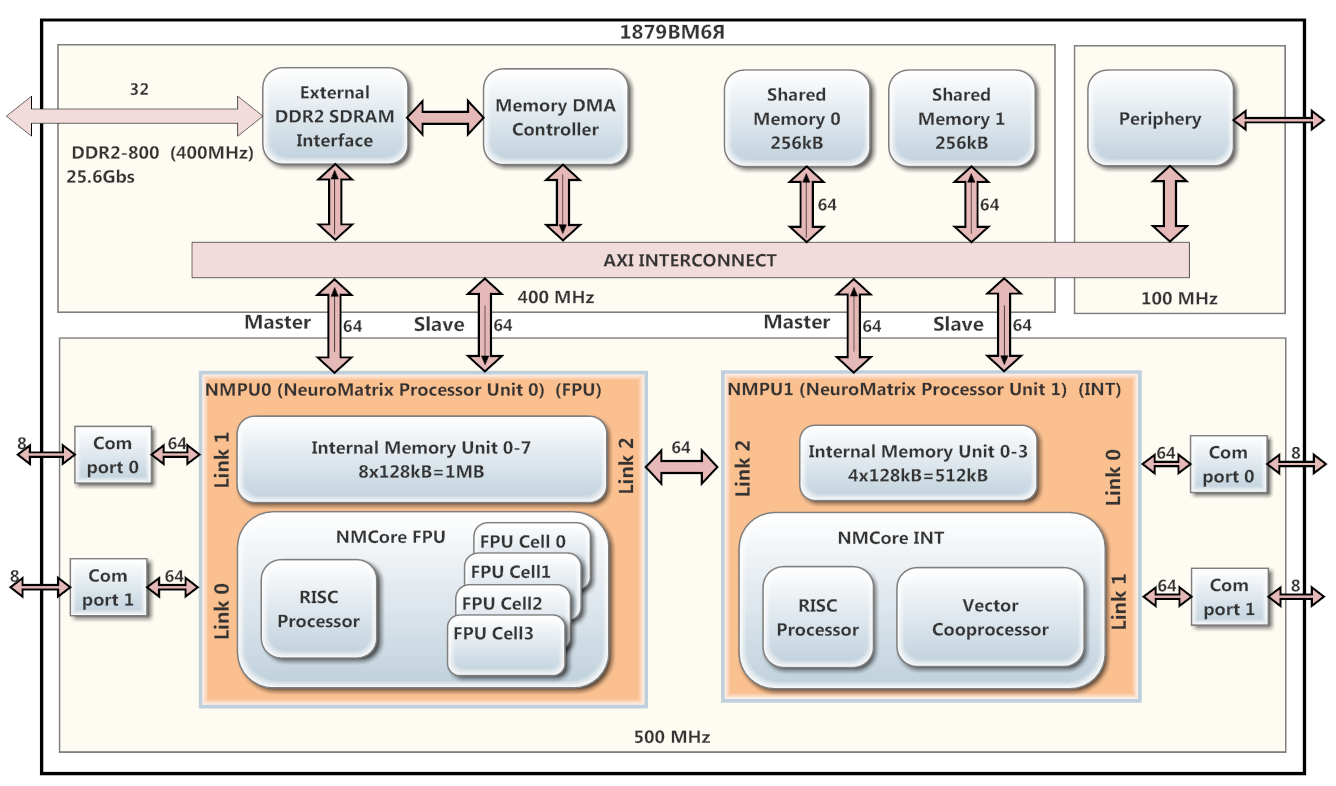Fig. 1. Schéma du processeur 1879VM6YA

Le processeur est situé sur le module instrument MC121.01 (voir. Fig. 2). Ce module dispose également de 512 Mo de mémoire DDR2.


Fig.2. MS121.01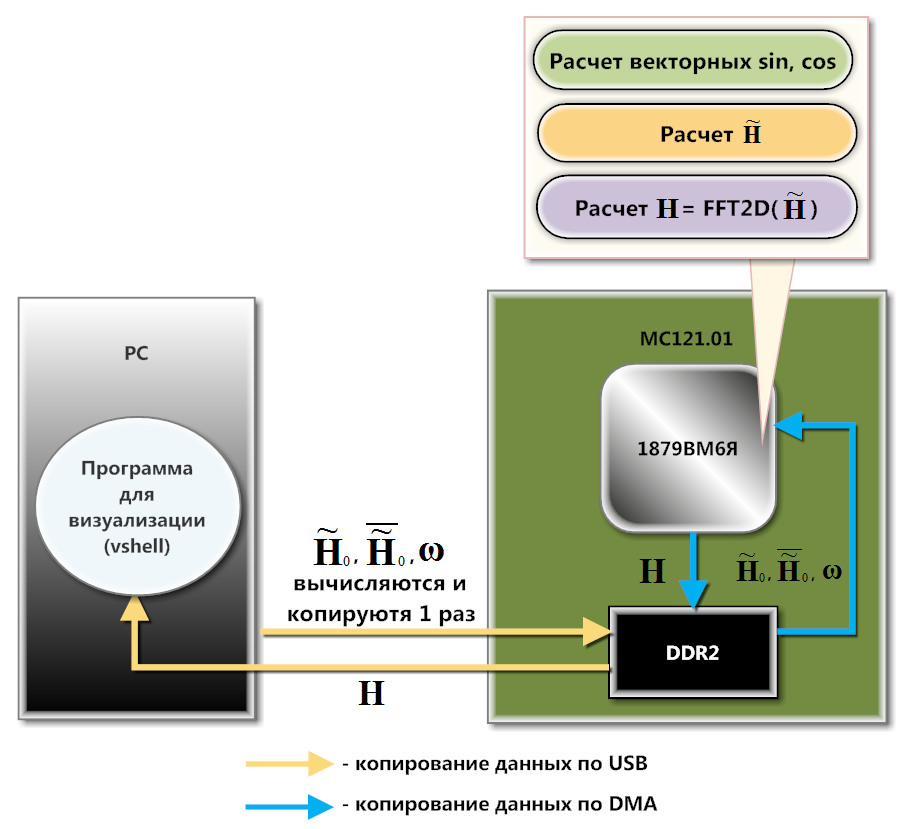



Fig. 3. Schéma d'interaction de MC121.01 et PC

Le MC121.01 interagit avec le PC via USB (schéma de la figure 3). Au niveau logiciel, cette interaction est organisée à l'aide de la bibliothèque de téléchargement et d'échange de données, qui fait partie du SDK de cette carte. Matrices précalculées $$$\ mathbf {\ widetilde H_0}$ , $$$\ overline {\ mathbf {\ widetilde H_0}}$ et $$$\ Large {\ mathbf ω}$ sont chargés dans la mémoire DDR2 via les fonctions de la bibliothèque de téléchargement et d'échange. Copies du contrôleur DMA $$$\ mathbf {\ widetilde H_0}$ , $$$\ overline {\ mathbf {\ widetilde H_0}}$ et $$$\ Large {\ mathbf ω}$ ligne par ligne dans la mémoire interne (SRAM) du processeur. Le téléchargement vers DDR2 est dû au fait qu'aucune de ces matrices ne s'intègre complètement dans SRAM. La copie ligne par ligne a lieu ici, car 1879BM6Ya calcule à partir de SRAM plus rapidement qu'à partir de DDR2. De plus, une partie importante des calculs peut être effectuée dans le contexte du DMA.

En utilisant les fonctions vectorielles de la bibliothèque NMPP pour calculer les sinus, les cosinus, la multiplication et l'ajout de vecteurs, le processeur calcule les lignes de la matrice $$$\ mathbf {\ widetilde H}$ et leur prend la FFT unidimensionnelle. Le résultat est renvoyé par DMA vers DDR2. Ainsi, en DDR2, une matrice intermédiaire est formée, à partir des colonnes dont le processeur calcule la FFT unidimensionnelle (après chargement des colonnes de la matrice intermédiaire par DMA dans SRAM). Ainsi, une matrice est formée en DDR2 $$$\ mathbf H$ . Cette matrice est téléchargée sur le PC pour dessiner une seule image avec l'image de la surface d'onde. Pour animer l'image en temps réel, vous devez calculer la matrice selon l'algorithme décrit ci-dessus $$$\ mathbf H$ en augmentant le paramètre t .

En pratique, il s'avère que 18796 calcule la matrice $$$\ mathbf H$ plus rapide que le PC ne le dégonfle. Pour cette raison, le processeur peut être inactif, attendant que le PC récupère le prochain lot de données. Il a été possible de résoudre ce problème en utilisant un tampon en anneau (contenant plusieurs matrices $$$\ mathbf H$ ) organisé en carte mémoire DDR2.

Au niveau logiciel, le travail avec le contrôleur DMA et le tampon en anneau est effectué à l'aide des fonctions de bibliothèque HAL (Hardware abstraction Level) pour les processeurs NeuroMatrix.

Visualisation de la surface des vagues

Quand le DEM $$$\ mathbf H$ chargé dans la mémoire du PC, vous pouvez visualiser la surface. Pour l'afficher plus clairement, vous devez coordonner x, y, z, décrivant les points sur la surface, multipliés par la matrice de rotation . Nous obtenons donc les nouvelles coordonnées de la surface x ', y', z ', en la tournant sous un certain angle.

En redimensionnant les nouvelles coordonnées et en reliant les points le long de celles-ci avec des lignes droites, vous pouvez voir l'animation des vagues de l'océan (voir la vidéo ci-dessous). Pour la visualisation de la surface, la bibliothèque permet d'afficher l'image sur l'écran vshell.

Conclusion

En conclusion, je veux dire que le calcul et la transmission via USB d'une matrice $$$\ mathbf H$ avec une taille de 256x256 nombres flottants, ~ 4,7 millions de cycles d'horloge sont dépensés (72 cycles d'horloge par flotteur). La fréquence d'images est ~ 107. Si vous ne tenez pas compte du temps nécessaire pour transférer les données via USB, les calculs coûteront environ 2,5 millions de cycles (38 cycles par flotteur). Il s'agit du temps total consacré par le processeur 18796 à la multiplication par élément et à l'ajout de matrices, au calcul de la FFT, aux sinus, aux cosinus et à la copie à l'aide de DMA. Ces calculs sont effectués dans le contexte du transfert de données USB.

La différence de 2,2 millions de cycles d'horloge (4,7 millions - 2,5 millions = 2,2 millions) indique que dans le système PC-MC121.01, l'USB est un «goulot d'étranglement», et 1879VM6YA peut être chargé de calculs de 46% de plus sans recevoir tirage FPS.

Je voudrais également noter que dans le contexte du transfert de données USB et des calculs sur un coprocesseur pour une virgule flottante, un coprocesseur pour l'arithmétique entière, qui n'a pas été utilisé dans cette tâche, peut être utilisé.

Le tableau montre les performances de certaines fonctions vectorielles de la bibliothèque nmpp.

Fonction	Bars
FFT unidimensionnelle, 256 points	1770
Sinus, 256 points	1400
Cosinus, 256 points	1400

Références:

NMPP - une bibliothèque de primitives pour l'architecture NeuroMatrix
HAL - Bibliothèque d'abstraction dépendante du matériel NeuroMatrix
VSHELL - bibliothèque d'images de traitement et d'affichage