Tâches du manuel scolaire I

Partie I
Partie II
Partie III

Considérons la solution algorithmique au problème numéro 38 du livre "Tâches pour les enfants de 5 à 15 ans"

Calculez le montant:

$$

$$\ frac {1} {1 \ cdot2} + \ frac {1} {2 \ cdot3} + \ frac {1} {3 \ cdot4} + ... + \ frac {1} {99 \ cdot100}$$

(avec une erreur ne dépassant pas 1% de la réponse)

Voici un algorithme pour calculer les sommes partielles de cette série dans Scheme (Lisp) dans drRacket (drRacket vous permet d'effectuer des calculs en fractions ordinaires):

#lang racket (define series_sum ( lambda (n) (if (= n 0) 0 (+ (/ 1 (* n (+ n 1))) (series_sum(- n 1))) ) ) ) (series_sum 10) (series_sum 100) (series_sum 1000) (series_sum 10000) (series_sum 100000) (series_sum 1000000) (define series_sum_1 ( lambda (n) (if (= n 0) 0 (+ (/ 1.0 (* n (+ n 1.0))) (series_sum_1(- n 1.0))) ) ) ) (series_sum_1 10) (series_sum_1 100) (series_sum_1 1000) (series_sum_1 10000) (series_sum_1 100000) (series_sum_1 1000000) 

Les deux derniers exemples drRacket calculés avec une erreur



Ce programme peut être exécuté sur ide ideone.com et codepad.org en ligne .



Si nous considérons des sommes partielles dans des fractions ordinaires, nous pouvons voir que la somme de la série est

$$

$$\ frac {n} {n + 1}$$

Permettez-moi de vous rappeler que $$$\ lim \ frac {n} {n + 1} = \ frac {1} {1+ \ frac {1} {n}} = \ frac {1} {1} = 1$ à $$$n \ to \ infty$

Le deuxième volume du cours de calcul différentiel et intégral 363 (4) examine le cas général

$$

$$\ sum \ frac {1} {(\ alpha + n) (\ alpha + n +1)} = \ frac {1} {\ alpha + 1}$$

La tâche du cours "Mathématiques pour les développeurs":
Trouver le nombre de membres dans une séquence $$$\ frac {2n-1} {4n + 5}$ allongé en dehors de l'intervalle $$$(1- \ frac {1} {1000}; 1+ \ frac {1} {1000})$

Passons au sujet principal de l'article.

Prenons un exemple de plus d'un livre de problèmes.
43 . Nombre de lapins (Fibonacci), forment une séquence $$$(a_ {1} = 1), 1, 3, 5, 8, 13, 21, 34, ...,$ dans lequel $$$a_ {n + 2} = a_ {n + 1} + a_ {n}$ pour tout le monde $$$n = 1, 2, ...$ . Trouvez le plus grand diviseur commun des nombres $$$a_ {100}$ et $$$a_ {99}$ .

Réponse: Deux nombres de Fibonacci adjacents sont des nombres premiers, c'est-à-dire $$$\ gcd (u_ {n + 1}, u_ {n}) = 1$
(Le pgcd est le plus grand commun diviseur, c'est-à-dire GCD).

«Preuve du livre« Au-delà des pages d'un manuel de mathématiques »[10-11]


Dans la tâche suivante, vous devez calculer le nombre d' or , $$$\ frac {\ sqrt {5} + 1} {2} \ environ 1 618$ . [Il s'agit du rapport d'aspect d'une carte postale qui reste similaire lors de la découpe d'un carré dont le côté est le plus petit côté de la carte postale.]

53 . Pour une séquence de nombres de Fibonacci $$$a_ {n}$ tâches 43 trouver la limite de la relation $$$\ frac {a_ {n + 1}} {a_ {n}}$ tout en s'efforçant $$$n$ à l'infini:

$$

$$\ frac {a_ {n + 1}} {a_ {n}} = 2, \ frac {3} {2}, \ frac {5} {3}, \ frac {8} {5}, \ frac { 13} {8}, \ frac {21} {13}, \ frac {34} {21}.$$

Considérons les segments représentant les différences de deux membres adjacents de la série $$$\ frac {a_ {n + 1}} {a_ {n}}$ .

Même les membres de la série $$$\ frac {a_ {n + 1}} {a_ {n}}$ représentent une séquence croissante $$$x_ {n}$

$$

$$\ frac {3} {2}, \ frac {8} {5}, \ frac {21} {13}, ...,$$

Membres de rang impair $$$\ frac {a_ {n + 1}} {a_ {n}}$ représentent une séquence décroissante $$$y_ {n}$

$$

$$2, \ frac {5} {3}, \ frac {13} {8}, ...,$$

Par le lemme d'intervalle intégré (Cours de calcul différentiel et intégral, 38)

$$

$$c = \ lim x_ {n} = \ lim y_ {n}$$

Pour notre ligne à un moment donné $$$c$ égalité équitable $$$\ frac {a_ {n + 2}} {a_ {n + 1}} = \ frac {a_ {n + 1}} {a_ {n}}$

Diviser $$$a_ {n + 2} = a_ {n + 1} + a_ {n}$ sur $$$a_ {n + 1}$ nous obtenons l'équation $$$\ frac {a_ {n + 2}} {a_ {n + 1}} = 1 + \ frac {a_ {n}} {a_ {n + 1}}$ .
En remplaçant $$$\ frac {a_ {n + 2}} {a_ {n + 1}} = x, \ frac {a_ {n}} {a_ {n + 1}} = \ frac {1} {x}$ nous obtenons l' équation quadratique $$$x = 1 + \ frac {1} {x}$ .

Si dans le programme geogebra nous connectons les points 2 et $$$\ frac {3} {2}$ , $$$\ frac {3} {2}$ et $$$\ frac {5} {3}$ , $$$\ frac {5} {3}$ et $$$\ frac {8} {5}$ etc. - obtenir un chiffre auto-similaire




En général, il existe un algorithme standard pour calculer les nombres de Fibonacci en Python.
Cet algorithme est disponible sur Python.org

 def fib(n): a, b = 0, 1 while a < n: print(a) a, b = b, a+b fib(100) 

Vous pouvez vérifier le lien
Modifiez cet algorithme pour qu'il imprime une approximation du nombre d'or. Pour deux nombres adjacents a et b, nous diviserons la somme a + b par b

 def fib(n): a, b = 0.0 , 1.0 while a < n: print((a+b)/b) a, b = b, a+b fib(100) 

Vous pouvez vérifier le lien

Voici quelques tâches du tutoriel SICP concernant le nombre d'or.


L'exemple suivant du livre de tâches "Tâches pour les enfants de 5 à 15 ans"
54 . Calculer la fraction continue infinie

$$

$$1 + \ frac {1} {2 + \ frac {1} {1+ \ frac {1} {2+ \ frac {1} {1+ \ frac {1} {2 + ...}}}}}$$

UPD Considérez l'équation

$$

$$\ alpha = 1+ \ frac {1} {2 + \ frac {1} {\ alpha}}$$

Selon les théorèmes 236 et 235 du livre «Number Theory»:

$$

$$\ alpha = \ frac {P_ {1} \ alpha + P_ {0}} {Q_ {1} \ alpha + Q_ {0}}$$

Nous composons un tableau de valeurs $$$P_ {n}$ et $$$Q_ {n}$ à $$$n = 0,1:$



pour que $$$\ alpha = \ frac {3 \ alpha + 1} {2 \ alpha + 1}, 2 \ alpha ^ {2} - 2 \ alpha -1 = 0$

et depuis $$$\ alpha> 0,$ alors

$$

$$\ alpha = \ frac {1 + \ sqrt {3}} {2}$$

Considérez le problème du livre «Derrière les pages d'un manuel de mathématiques» [10-11]
4 . Afficher ce numéro $$$\ sqrt {1+ \ sqrt {1 + \ sqrt {1 + ...}}}$ égal au nombre $$$\ varphi$ définir le nombre d'or.

Considérez l' option $$$x_ {n} = \ sqrt {c + \ sqrt {c + ... + \ sqrt {c}}}$
Cours de calcul différentiel et intégral, 35 (2)

De cette façon $$$x_ {n + 1}$ obtenu de $$$x_ {n}$ selon la formule

$$

$$x_ {n + 1} = \ sqrt {c + x_ {n}}$$

... Par le théorème principal, les options $$$x_ {n}$ a une limite finie $$$a$ . Pour le déterminer, on passe à la limite de l'égalité

$$

$$x_ {n + 1} ^ {2} = c + x_ {n};$$

Nous obtenons de telle manière que $$$a$ satisfait l'équation quadratique

$$

$$a ^ {2} = c + a$$

Cette équation a les racines de différents signes; mais la limite qui nous intéresse $$$a$ ne peut pas être négatif, par conséquent, il est exactement égal à la racine positive:

$$

$$a = \ frac {\ sqrt {4c + 1} + 1} {2}$$

D'où nous pouvons conclure que le "nombre d'or" est une solution à l'équation $$$a ^ {2} = c + a$
à $$$c = 1$ .


De plus, dans le cours du calcul différentiel et intégral, 35 (3), un algorithme pour calculer le nombre inverse est considéré

Soit $$$c$ Est un nombre positif et mettez $$$x_ {n} = cy_ {n}$ . La relation de récursivité écrite ci-dessus sera remplacée par:

$$

$$y_ {n + 1} = y_ {n} (2 - cy_ {n})$$

Prendre la valeur initiale $$$y_ {0}$ sous la condition: $$$0 <y_ {0} <\ frac {1} {c}$ nous obtenons cela $$$y_ {n}$ augmente de façon monotone, aura tendance à $$$\ frac {1} {c}$ . Selon ce schéma, sur les machines à compter, le nombre inverse est calculé $$$c$ .

Algorithme de calcul des nombres inverses $$$c$ en Python:
( Ideone.com et codepad.org )

 def reciprocal(c,y0,n): arr=[] for i in range(n): arr.append(y0) y0=y0*(2-c*y0) return arr 

La fonction réciproque prend un nombre en entrée $$$c$ valeur initiale $$$y_ {0}$ , nombre d'itérations $$$n$ et renvoie un tableau "d'approximations" au nombre $$$\ frac {1} {c}$ .
$$$y_ {0} = 0,1$ à $$$c <10$
$$$y_ {0} = 0,01$ à $$
$$$y_ {0} = 0,001$ à $$
etc.
Exemples de fonctionnement de la fonction réciproque avec divers $$$c$

 >>> reciprocal(3,0.1,10) 

[0,1, 0,17, 0,2533, 0,31411733000000003, 0,3322255689810133, 0,3333296519077525,
0.3333333332926746, 0.3333333333333333337, 0.3333333333333333337, 0.3333333333333333337]

 >>> reciprocal(8,0.1,10) 

[0,1, 0,12, 0,1248, 0,12499968, 0,1249999999991808, 0,125, 0,125, 0,125, 0,125, 0,125]

 >>> reciprocal(5,0.1,10) 

[0,1, 0,15000000000000002, 0,18750000000000003, 0,19921875000000003, 0,19999694824218753, 0,1999999999534339, 0,20000000000000004, 0,1999999999999999998,
0,1999999999999999998, 0,1999999999999999998]

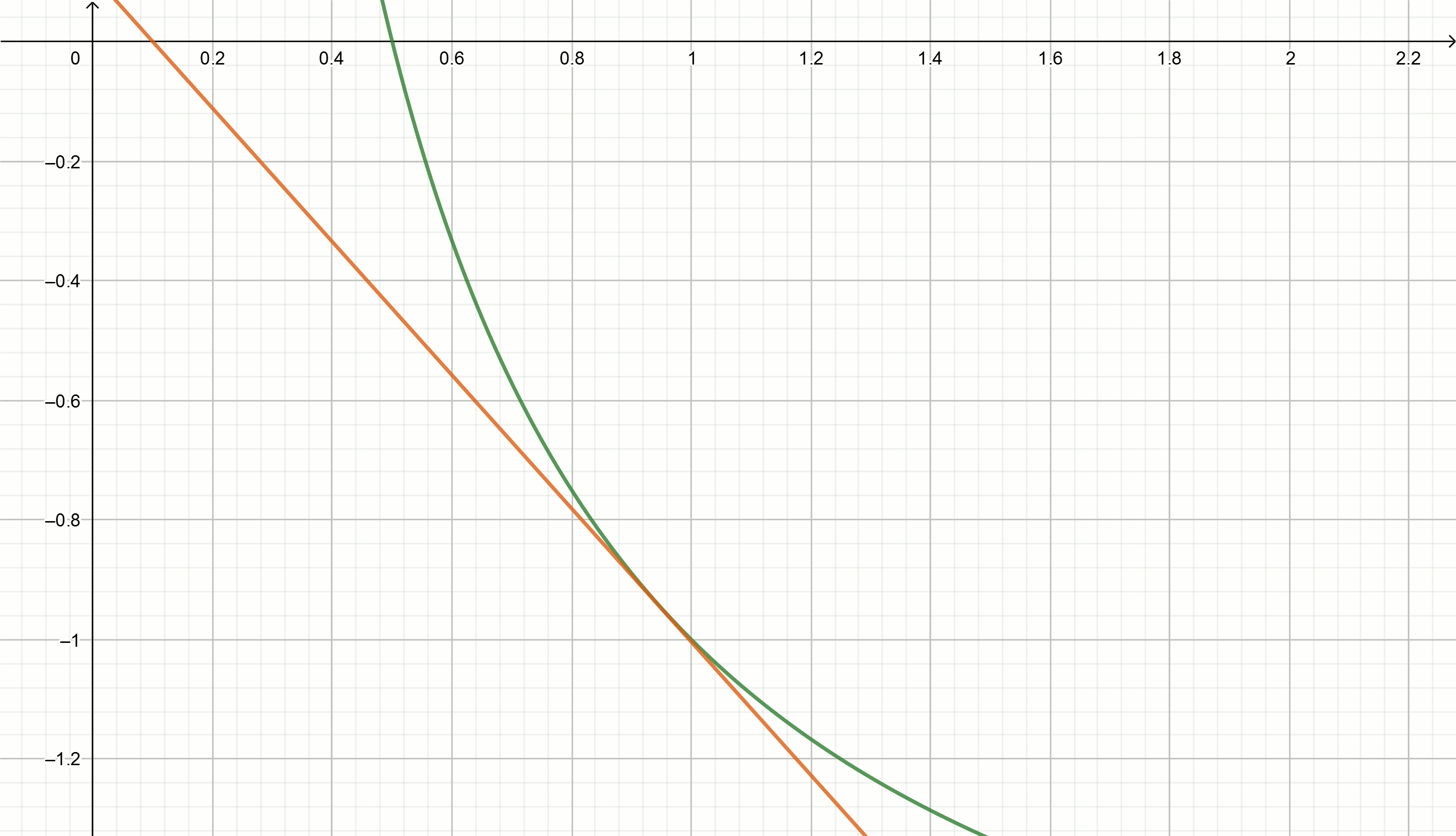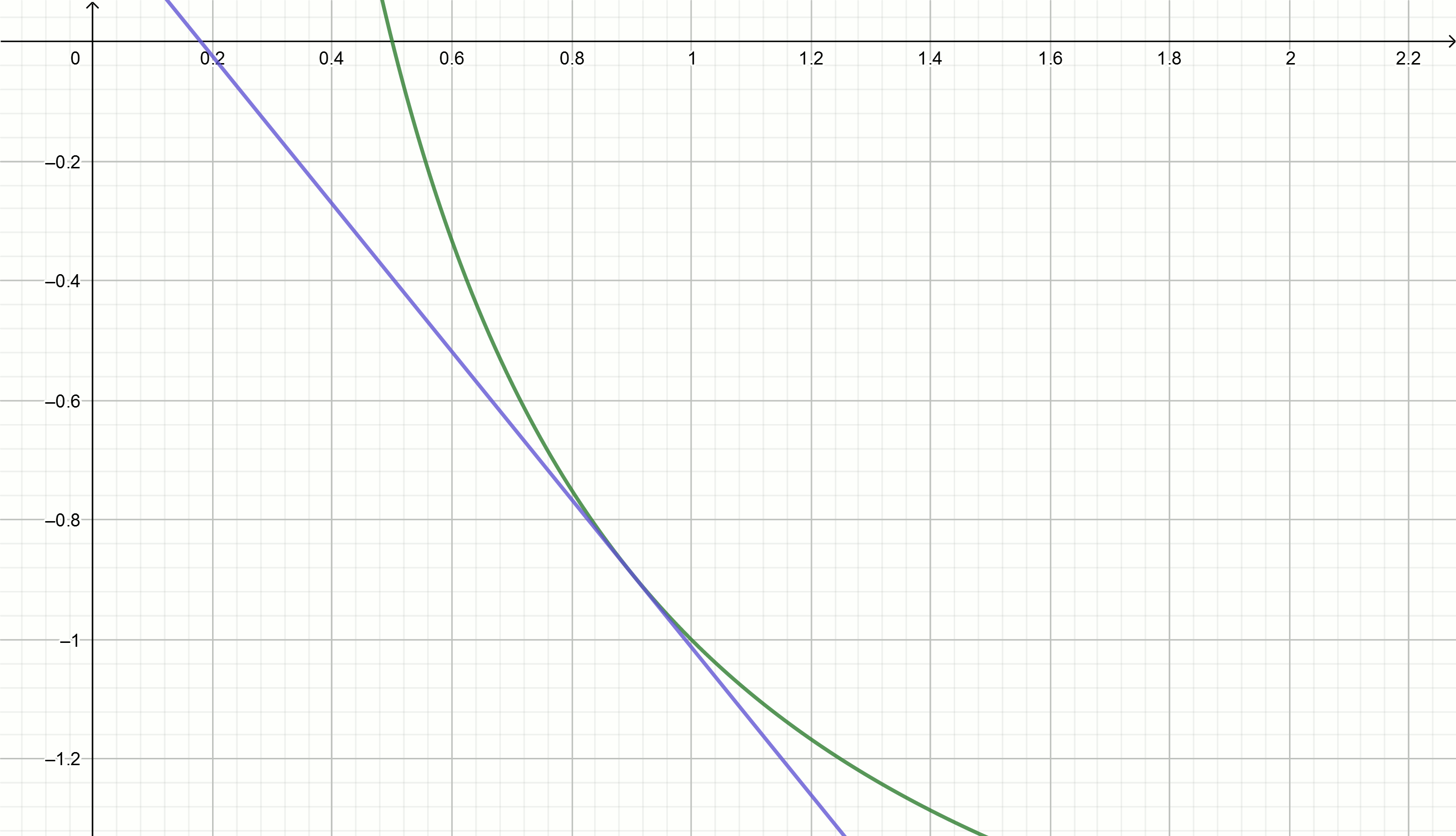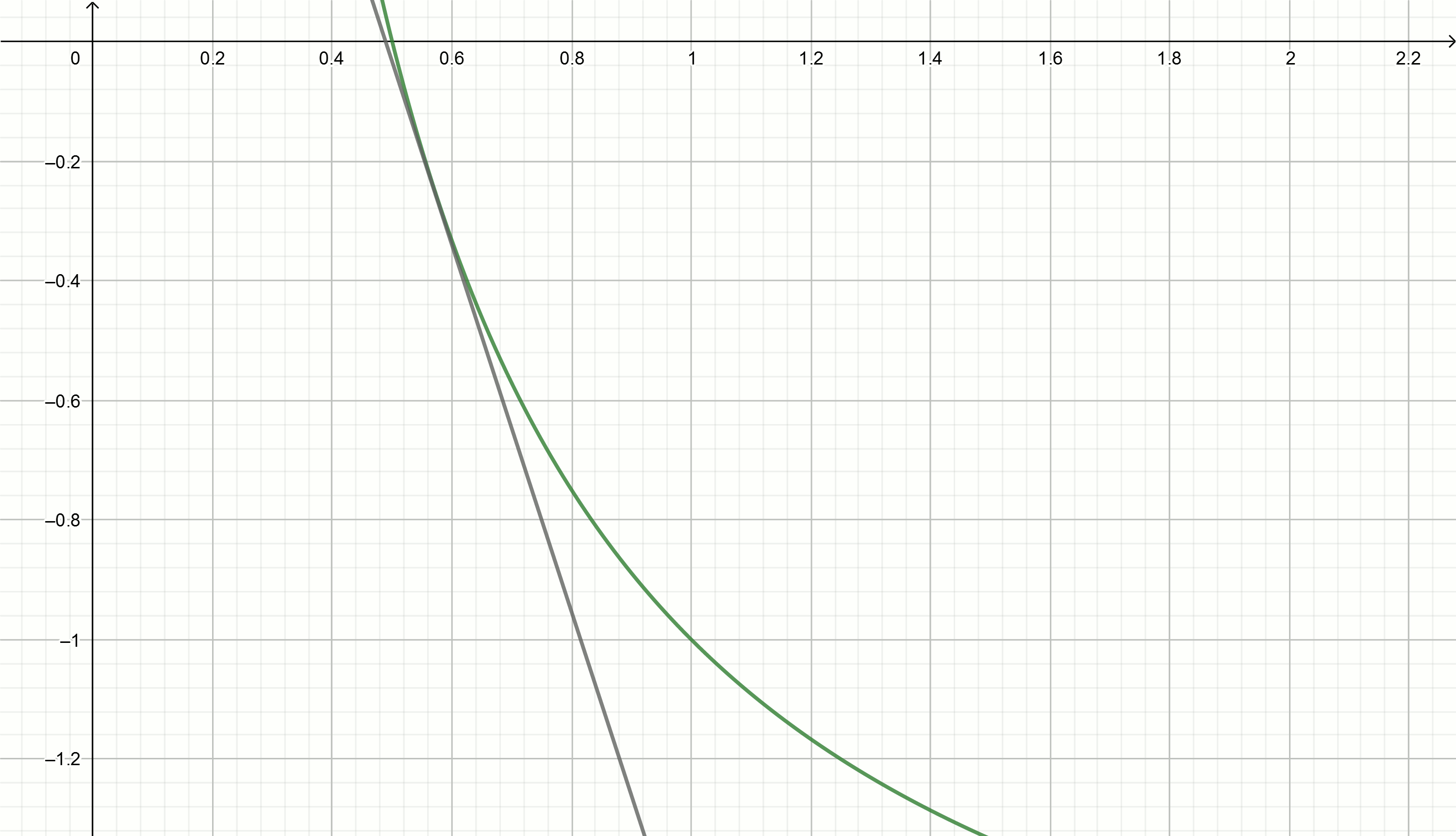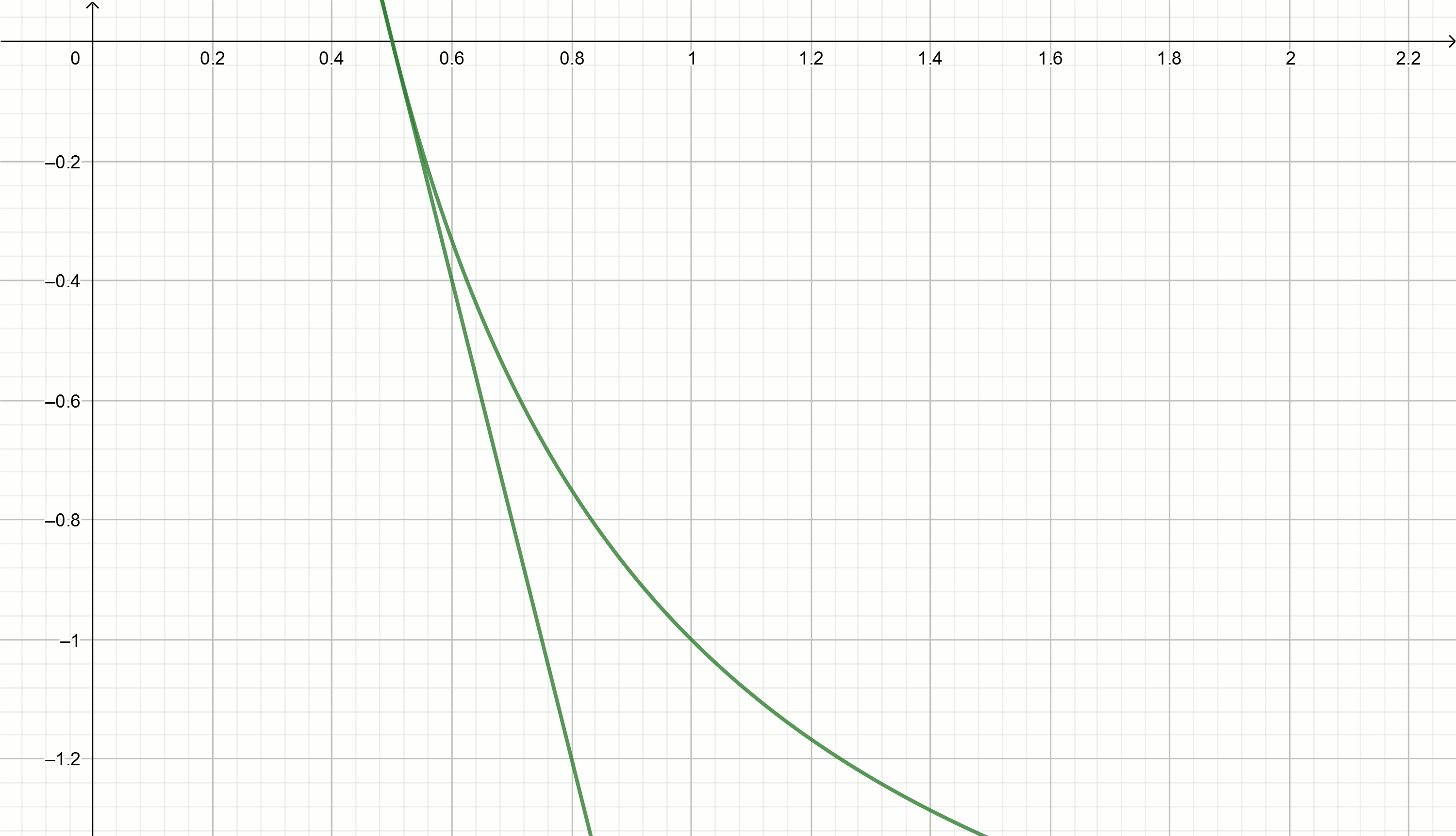
Interprétation géométrique

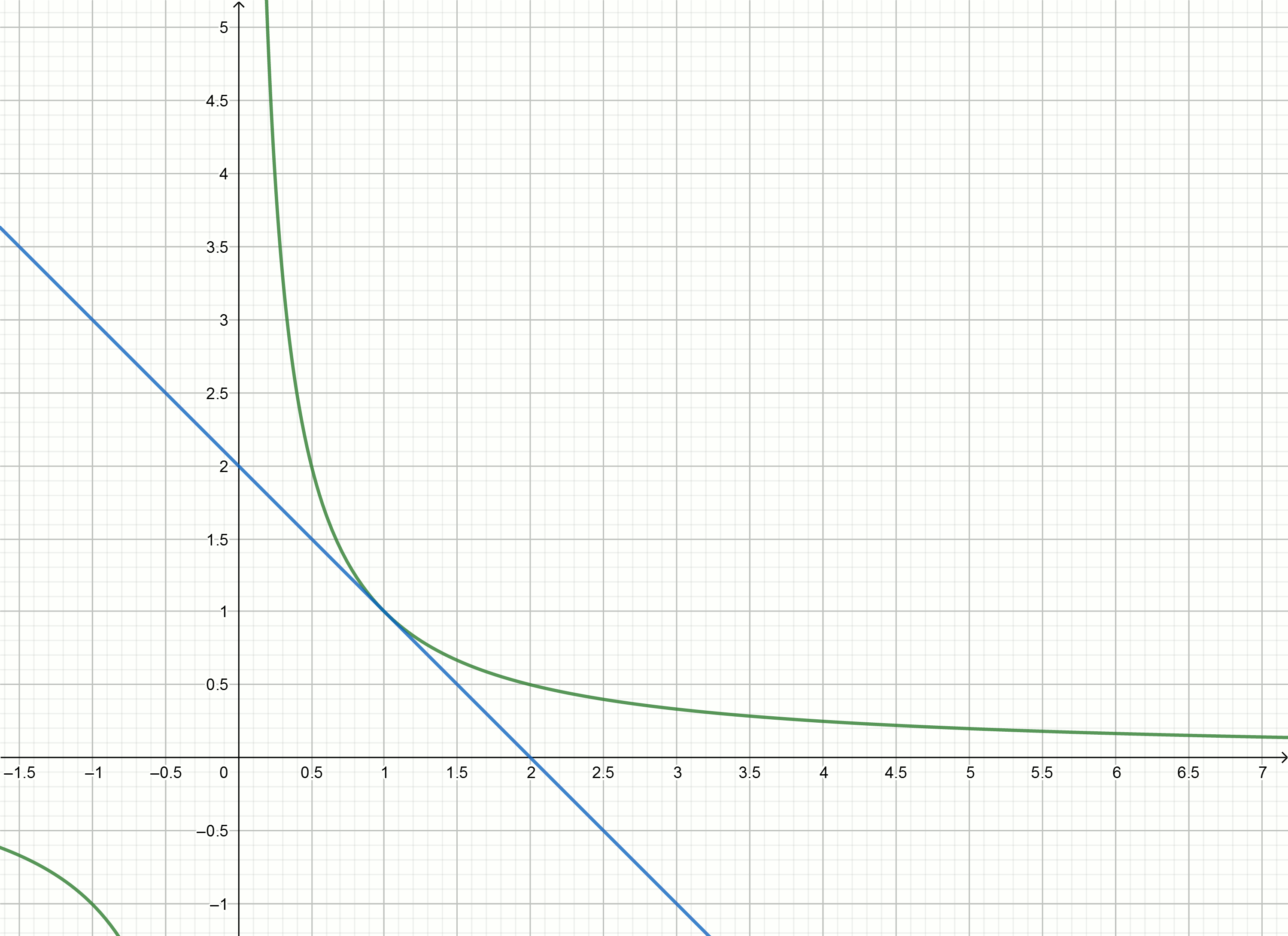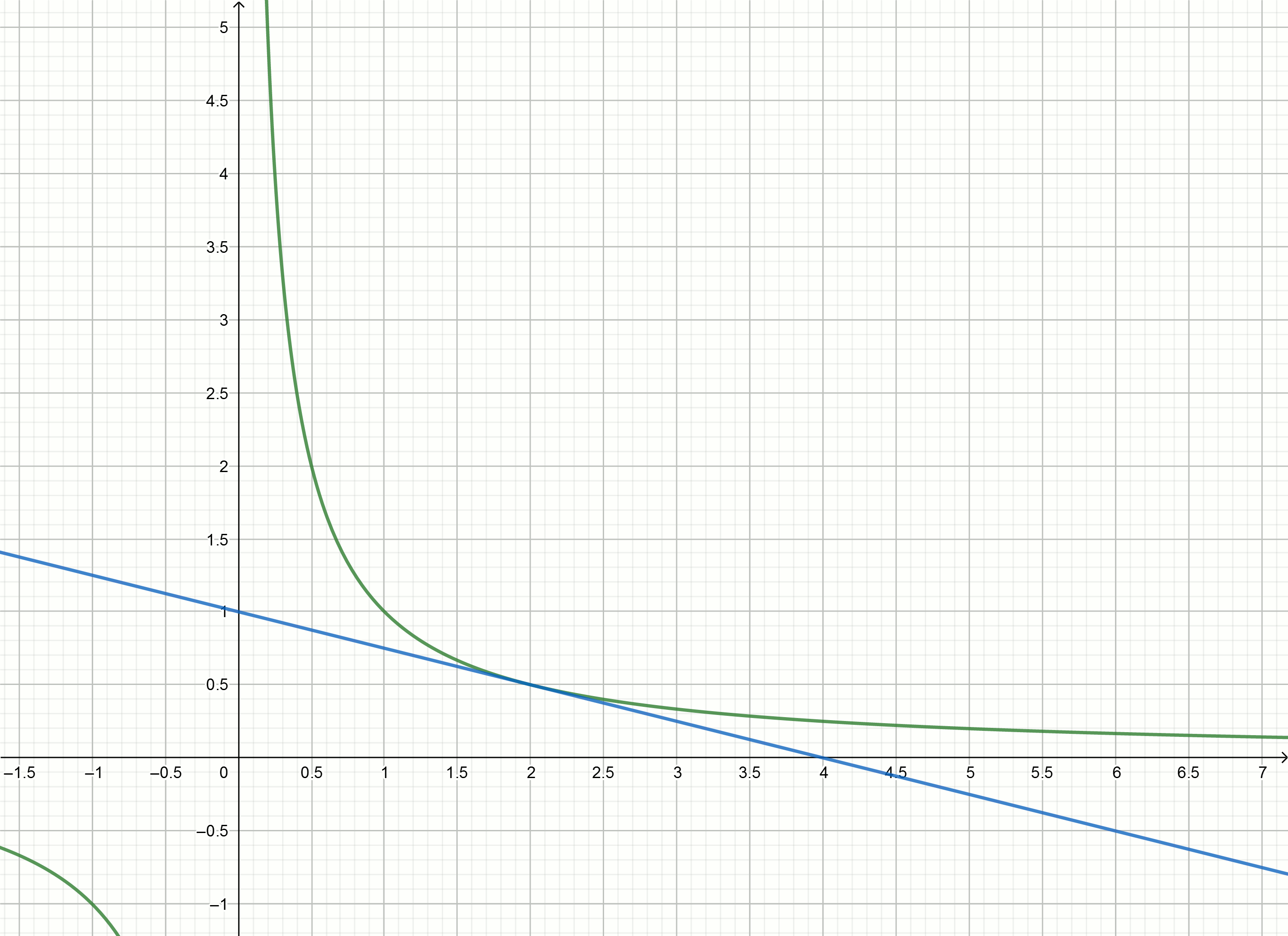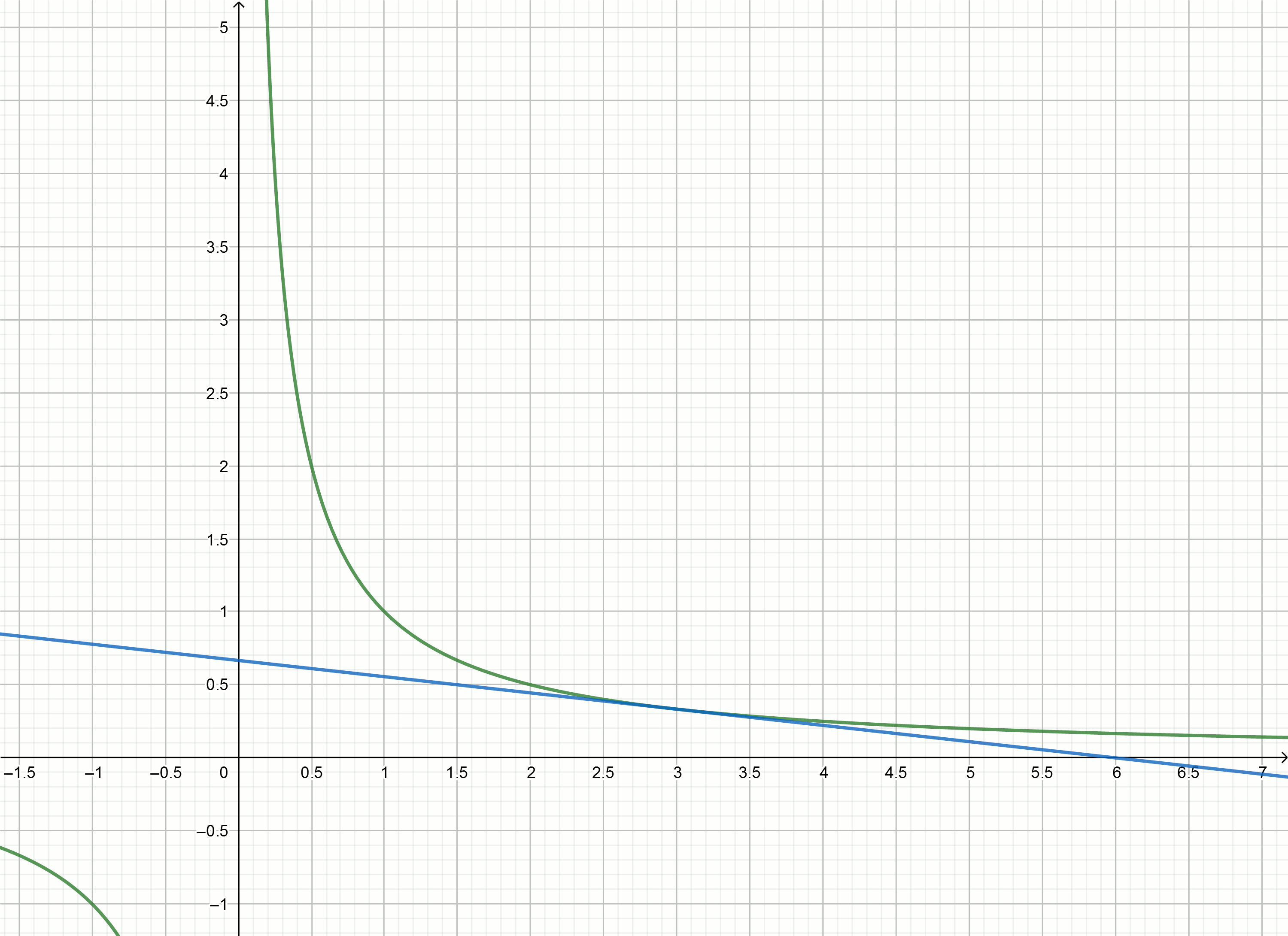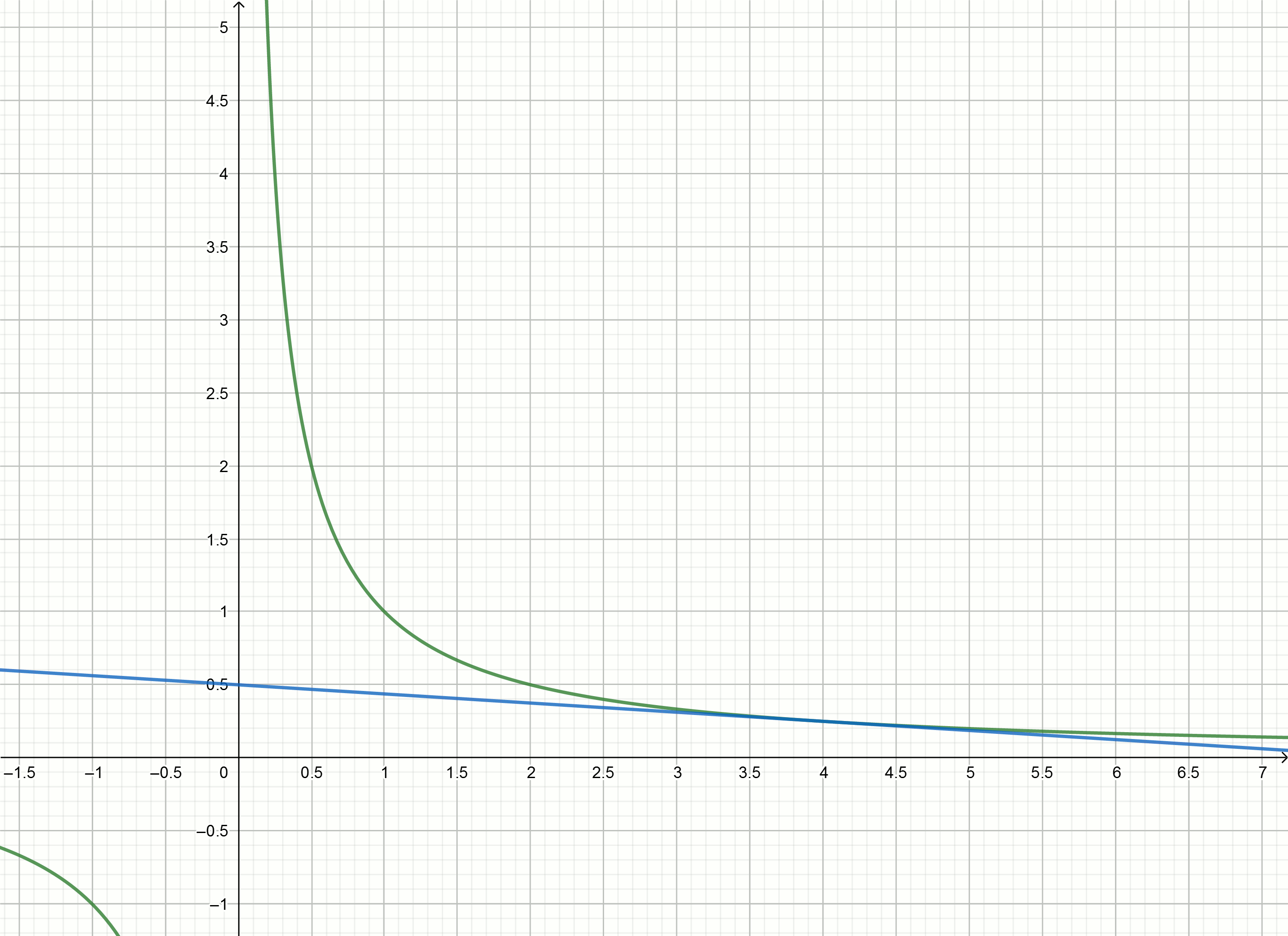
Essayons d'utiliser la méthode tangente pour approximer le nombre inverse.
Tangentes $$$y = f '(x_ {0}) (x-x_ {0}) + f (x_ {0})$ graphique de fonction $$$y = \ frac {1} {x}$ sont exprimés par la formule $$$y = \ frac {2} {x_ {0}} - \ frac {x} {x_ {0} ^ {2}}$

Substitution de nombres $$ au lieu de $$$x_ {0}$ on obtient les équations des tangentes

$$

$$y = 2-x$$

$$

$$y = 1- \ frac {x} {4}$$

$$

$$y = \ frac {2} {3} - \ frac {x} {9}$$

$$

$$y = \ frac {1} {2} - \ frac {x} {16}$$

Construisez ces graphiques


Si vous déplacez l'hyperbole vers le bas pour $$$\ alpha$ , puis il traverse l'axe des abscisses au point $$$\ frac {1} {\ alpha}$ .
L'équation tangente est convertie en $$$y = \ frac {2} {x_ {0}} - \ frac {x} {x_ {0} ^ {2}} - \ alpha$
En outre, l'équation de l'équation de la tangente à zéro et l'expression $$$x$ nous obtenons l'équation $$$x = x_ {0} - \ frac {f (x_ {0})} {f '(x_ {0})}$

Au lieu de cela $$$f (x_ {0})$ remplaçant $$$\ frac {1} {x_ {0}} - \ alpha$
Au lieu de cela $$$f '(x_ {0})$ remplaçant $$$- \ frac {1} {x_ {0} ^ {2}}$

Nous obtenons l'expression $$$x = x_ {0} + (\ frac {1} {x_ {0}} - \ alpha) x_ {0} ^ {2}$
En élargissant les supports, nous obtenons $$$x = x_ {0} + x_ {0} - \ alpha x_ {0} ^ {2}$

Remplaçant $$ dans l'équation $$$x = x_ {0} (2- \ alpha x_ {0})$ et voir quelles valeurs vont "traverser" $$$x$ à $$$\ alpha = 2$ nous obtenons $$

Substitution de ces valeurs dans l'équation $$$y = \ frac {2} {x_ {0}} - \ frac {x} {x_ {0} ^ {2}} - 2$ nous devenons directs

$$

$$y = 0,111 - \ frac {x} {0,897}$$

$$

$$y = 0,222 - \ frac {x} {0,81}$$

$$

$$y = 0,816 - \ frac {x} {0,504}$$

$$

$$y = 0,857 - \ frac {x} {0,49}$$

$$

$$y = 1,5 - \ frac {x} {0,326}$$

$$

$$y = 2 - \ frac {x} {0,25}$$

Extraction de racine carrée

Revenant aux expressions irrationnelles, nous considérons une méthode itérative d'extraction de la racine carrée.
Nous allons écrire un algorithme en utilisant la méthode itérative Heron

$$

$$x_ {n + 1} = \ frac {1} {2} (x_ {n} + \ frac {a} {x_ {n}})$$

 def square_root(a,n): # a -  , n -   x0=1 #    1 arr=[] for i in range(n): arr.append(x0) #      x0=0.5*(x0+a/x0) #      return arr print square_root(2,10) 

codepad.org

Calcul de la racine carrée à l'aide des fractions continues utilisées par Rafael Bombelli

Pour trouver la valeur $$$\ sqrt {n}$ , on définit d'abord toute son approximation: $$$\ sqrt {n} = a \ pm r$ où $$ . Alors $$$n = (a \ pm r) ^ {2} = a ^ {2} \ pm 2ar + r ^ {2}$ . De là, il est facile de déduire que $$$r = {\ frac {| n-a ^ {2} |} {2a \ pm r}}$ . Remplacement de l'expression résultante dans la formule $$$\ sqrt {n} = a \ pm r$ , nous obtenons une expansion continue des fractions:

$$

$$a \ pm {\ frac {| na ^ {2} |} {2a \ pm {\ frac {| na ^ {2} |} {2a \ pm {\ frac {| na ^ {2} |} {2a \ pm \ cdots}}}}}}$$

Ainsi, nous pouvons écrire l'algorithme d'extraction de racine carrée en utilisant la décomposition en une fraction continue

 def square_root(n,a,n_count): # n- , a -    x0=a #    a arr=[] for i in range(n_count): #       a arr.append(x0-a) #  a x0=2*a+(na*a)/x0 return arr print square_root(2.0,1.0,10) 

codepad.org

En général, les nombres réels et complexes, ainsi que les fonctions d'une ou plusieurs variables, peuvent être des numérateurs et des dénominateurs privés.
La méthode d'extraction de la partie entière permet de représenter un nombre irrationnel sous la forme d'une fraction continue infinie avec des unités dans les numérateurs (numérateurs fréquents égaux à l'unité).
Voici un exemple d'une expansion fractionnelle continue d'un nombre $$$\ sqrt {5}$ extrait du livre "Algèbre"

$$

$$\ sqrt {5} -2 = \ frac {(\ sqrt {5} -2) (\ sqrt {5} +2)} {\ sqrt {5} +2} = \ frac {1} {\ sqrt { 5} +2}$$

De cette façon $$$\ sqrt {5} = 2+ \ frac {1} {\ sqrt {5} +2}$

Sélectionnez la partie entière du nombre $$$\ sqrt {5} +2: E (\ sqrt {5} +2) = 4$ . Moyens $$$\ sqrt {5} +2$ peut être représenté comme $$ . Il est clair que $$$\ alpha = \ sqrt {5} + 2-4 = \ sqrt {5} -2$ donc $$$\ sqrt {5} + 2 = 4 + \ sqrt {5} + 2$ . Encore une fois, nous détruisons l'irrationalité dans le numérateur du deuxième terme:

$$

$$\ sqrt {5} -2 = \ frac {1} {\ sqrt {5} +2}$$

Le résultat est:

$$

$$\ sqrt {5} = 2 + \ frac {1} {4+ \ frac {1} {\ sqrt {5} +2}}$$

Faisons une autre étape similaire:

$$

$$\ sqrt {5} = 2 + \ frac {1} {4+ \ frac {1} {4+ \ frac {1} {\ sqrt {5} +2}}}$$

Il est facile de voir que le processus d'isolement de la partie entière et la formation d'une fraction continue dans cet exemple n'a pas de fin. Dans chaque nouveau dénominateur apparaîtra $$$4$ et terme $$$\ sqrt {5} -2$ . Il est donc clair que $$$\ sqrt {5}$ est représentée comme une fraction continue infinie:

$$

$$\ sqrt {5} = [2, 4, 4, 4, ...]$$

Hypothèse

Si $$$d \ in \ mathbb {N}, \ sqrt {d} \ notin \ mathbb {N}$ puis la fraction continue du nombre $$$\ sqrt {d} + [\ sqrt {d}]$ purement périodique.
Evarist Galois a prouvé cette hypothèse.

C'est-à-dire si à la partie non périodique de la fraction $$$[1; 2,2,2, ...] = \ sqrt {2}$ ajouter toute la partie $$$[\ sqrt {2}] = 1$ alors nous obtenons une fraction purement périodique $$ .

$$$\ sqrt {3} = [1; 1,2, ...];$
$$$\ sqrt {3} +1 = [2,1, ...]$

$$$\ sqrt {5} = [2; 4,4,4, ...];$
$$$\ sqrt {5} +2 = [4,4,4, ...]$

$$$\ sqrt {6} = [2; 2,4, ...];$
$$$\ sqrt {6} +2 = [4,2, ...]$

$$$\ sqrt {13} = [3; 1,1,1,1,6, ...];$
$$$\ sqrt {13} +3 = [6,1,1,1,1,1, ...]$


Si dans la décomposition racine selon la méthode Bombelli

$$

$$\ sqrt {n} = a \ pm {\ frac {| na ^ {2} |} {2a \ pm {\ frac {| na ^ {2} |} {2a \ pm {\ frac {| na ^ { 2} |} {2a \ pm \ cdots}}}}}}} $$$

ajouter au premier terme $$$a$ , on obtient une fraction purement périodique

$$

$$\ sqrt {n} + a = 2a \ pm {\ frac {| na ^ {2} |} {2a \ pm {\ frac {| na ^ {2} |} {2a \ pm {\ frac {| na ^ {2} |} {2a \ pm \ cdots}}}}}}}$$

Il reste à amener la fraction à une forme plus familière (avec des unités au numérateur).
Divisez le numérateur et le dénominateur de la fraction par $$$| n-a ^ {2} |$ nous obtenons l'expression

$$

$$\ sqrt {n} + a = 2 a \ pm {\ frac {1} {\ frac {2a} {| na ^ {2} |} \ pm {\ frac {1} {2a \ pm {\ frac { 1} {\ frac {2a} {| na ^ {2} |} \ pm \ cdots}}}}}}}$$

De cette façon

$$

$$\ sqrt {2} +1 = 2+ \ frac {1} {\ frac {2} {1} + \ frac {1} {2 + \ frac {1} {\ frac {2} {1} +. ..}}} = [2,2,2, ...]$$

$$

$$\ sqrt {3} +1 = 2+ \ frac {1} {\ frac {2} {2} + \ frac {1} {2 + \ frac {1} {\ frac {2} {2} +. ..}}} = [2,1, ...]$$

$$

$$\ sqrt {5} +2 = 4+ \ frac {1} {\ frac {4} {1} + \ frac {1} {4 + \ frac {1} {\ frac {4} {1} +. ..}}} = [4,4,4, ...]$$

$$

$$\ sqrt {6} +2 = 4+ \ frac {1} {\ frac {4} {2} + \ frac {1} {4 + \ frac {1} {\ frac {4} {2} +. ..}}} = [4,2, ...]$$

$$

$$\ sqrt {13} +3 = 6+ \ frac {1} {\ frac {6} {4} + \ frac {1} {6 + \ frac {1} {\ frac {6} {4} +. ..}}} = [6, \ frac {3} {2}, ...]$$

Nous allons écrire un programme qui calcule l'approximation de la fraction continue $$$[6, \ frac {3} {2}, ...]$

 #lang racket (define continued_fraction ( lambda (n) (if (= n 0) 1 (+ 6 (/ 1 (+ 3/2 (/ 1 (continued_fraction(- n 1)))))) ))) (continued_fraction 4) 

codepad.org
Dans la quatrième étape, nous obtenons $$ ce qui est égal $$ tout $$$\ sqrt {13} +3 \ environ 6,60555127$ .




PS Résoudre le problème («Problèmes pour les enfants de 5 à 15 ans»)
27 . Prouver que le reste de la division d'un nombre $$$2 ^ {p-1}$ premier impair
$$$p$ est égal à $$$1$
(exemples: $$$2 ^ {2} = 3a + 1, 2 ^ {4} = 5b + 1, 2 ^ {6} = 7c + 1, 2 ^ {10} -1 = 1023 = 10 \ cdot 93)$ .
Ce problème est examiné dans l'article Amazing Adventures of Continued Fractions du magazine Quantum.

Livres:
"Tâches pour les enfants de 5 à 15 ans" V. I. Arnold.
«Le cours du calcul différentiel et intégral» G. M. Fichtenholtz
"Théorie des nombres" A. A. Buchstab
«Derrière les pages d'un manuel de mathématiques» N. Ya. Vilenkin, L. P. Shibasov, Z. F. Shibasova
«Algèbre» N. Ya. Vilenkin, R. S. Guter, S. I. Schwarzburd
Arithmétique numérique Ercegovac Milos D., Lang Tomas
«La structure et l'interprétation des programmes informatiques» Harold Abelson, Gerald Sassman

Voir aussi
L'article "Sur une tâche qui n'est plus proposée lors de l'entretien".
Le blog de Spice IT Recruitment publie des tâches d'entrevue dans diverses entreprises.
Tâches pour les interviews dans Yandex.
Dans cette vidéo, A. Savvateev résout des problèmes avec des interviews chez Tesla.