Comment sont les indicateurs techniques sur les marchés boursiers

Quiconque a déjà été intéressé par les marchés boursiers ou de crypto-monnaie a vu ces lignes supplémentaires. Et vous avez probablement entendu des opinions de commerçants chevronnés selon lesquels ils ne fonctionnent pas et comment ils n'utilisent rien. Mais ils aident beaucoup et mon terminal de trading, que je regarde paresseusement une fois par jour, ressemble à l'image ci-dessous.

Comment sont-ils tous pareils? Et à qui cela peut-il être utile? Vous devriez certainement vous familiariser avec cela si:

1. Vous les utilisez dans votre métier
2. Envisagez-vous d'écrire un robot de trading
3. Voulez-vous mettre en œuvre une stratégie de trading vous-même

Un indicateur technique est le plus souvent une fonction de fenêtre, de poids ou de récurrence des prix et des volumes qui proviennent de l'échange sous la forme d'un tableau de bougies TOHLCV (temps unix, ouvert, haut, bas, fermé, volume). Divers filtres, maximum-minimum ou autres indicateurs peuvent également être utilisés comme base pour les calculs ultérieurs.

Moyenne mobile (SMA)

Lors de la mise en œuvre des indicateurs, il est très pratique d'utiliser une approche de programmation fonctionnelle. Par exemple, une moyenne mobile, c'est juste la moyenne de chaque valeur de la fonction de fenêtre mobile au prix de clôture

function sma($close, window) { return rolling(x => mean(x), window, $close); } 

où la fonction mean () est la valeur moyenne, le paramètre window est la taille de la fenêtre, et rolling () est une combinaison de la fonction window, qui pour chaque cellule actuelle du tableau produit un tableau des n derniers éléments, et l'opération qui minimise la fenêtre à un certain nombre.

 function rolling(operation, window, array) { let result = []; for (let i = 0; i < array.length; i++) { if (i + 1 < window) { result.push(NaN); } else { result.push(operation(array.slice(i + 1 - window, i + 1))); } } return result; } 

La moyenne mobile est un indicateur en retard et permet de déterminer la tendance. Il est superposé sur le graphique des prix et les premières valeurs sont généralement ignorées.



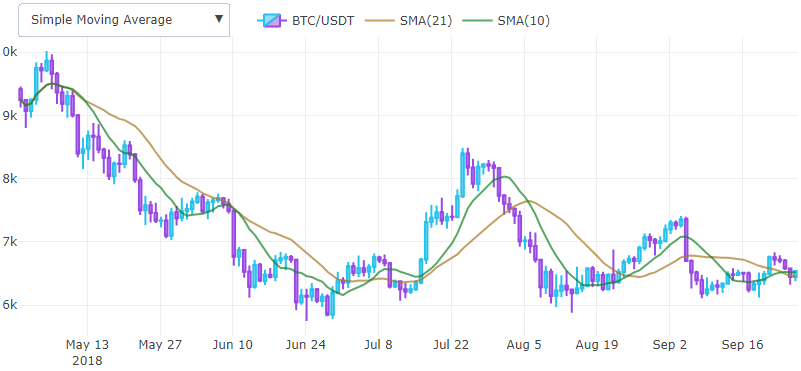
Habituellement, une paire d'indicateurs est prise en compte et le point où un indicateur à fenêtre courte croise un indicateur à fenêtre longue est considéré comme un point d'entrée potentiel par le bas et un point de sortie par le haut. En pratique, une moyenne mobile exponentiellement pondérée est plus souvent utilisée, en utilisant une fonction de fenêtre pondérée pour réduire l'effet de retard.

Écart type (STDEV)

Si nous remplaçons la fonction mean () dans la version précédente par la racine de la variance sd (), nous obtiendrons un écart-type mobile.

 function stdev($close, window) { return rolling(x => sd(x), window, $close); } 

La dispersion est considérée comme habituelle de la manière habituelle, le plus souvent sans correction de Bessel. La racine de la variance est également utilisée, car la variance elle-même est mesurée en roubles carrés / dollars.

Bandes de Bollinger (BB)

Ainsi, nous avons déjà reçu deux indicateurs de base qui peuvent déjà être combinés et en recevoir de nouveaux. Par exemple, si nous ajoutons point par point la moyenne mobile et l'écart type, tout en multipliant par 2, nous obtenons la partie supérieure de la bande de Bollinger, et si nous soustrayons la partie inférieure.



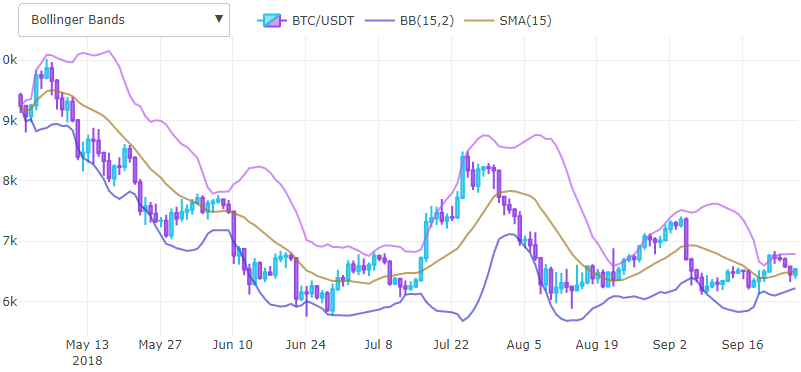
En code, cela ressemblera à ceci

 function bb($close, window, mult) { let middle = sma($close, window); let upper = pointwise((a, b) => a + b * mult, middle, stdev($close, window)); let lower = pointwise((a, b) => a - b * mult, middle, stdev($close, window)); return { lower : lower, upper : upper}; } 

où la fonction point par point ne fait rien d'autre que recueille un élément à partir de deux tableaux en utilisant l'opération qui lui est donnée.

Les bandes de Bollinger aident à déterminer l'accalmie avant un mouvement de prix important et sont utilisées comme un outil pour afficher facilement la volatilité sur un graphique; l'écart-type ne peut pas être affiché en superposition sur un graphique avec le prix, il est donc pratique de la reporter de la moyenne mobile.



Moyenne mobile pondérée exponentiellement (EMA)

Comment réduire le décalage de la moyenne mobile? Étant donné que lors du calcul, n derniers prix de clôture sont additionnés, vous pouvez comprendre que vous pouvez ajouter avec un certain poids, réduisant la contribution des anciens prix. Nous arrivons ainsi à la formule d'une fonction de fenêtre pondérée.

$$

$$\ bar x = \ frac {\ sum x_i} {N} = \ frac {\ sum 1 \ cdot x_i} {\ sum 1} \ quad \ Rightarrow \ quad \ widetilde {x} = \ frac {\ sum x_i w_i } {\ sum w_i}$$

si $$$w_i = q ^ i$ et choisissez une sorte de constante $$$q$ moins d'un, alors nous obtenons un poids infiniment décroissant, si en même temps nous additionnons les prix à partir du plus récent.



Les calculs peuvent être grandement simplifiés si la contribution des queues n'est pas prise en compte. En étendant la taille de la fenêtre sur toute sa longueur, vous pouvez obtenir une définition récursive.

$$

$$1 + q + q ^ 2 + ... + q ^ n \ underset {n \ to \ infty} {\ underset {q <0} {\ approx}} \ frac {1} {1-q} \\ \ mathrm {EMA} _ {curr} = \ frac {\ sum x_i q ^ i} {\ sum q ^ i} \ approx (1-q) \ sum x_i q ^ i \\ \ mathrm {EMA} _ {next } = \ frac {x_ {suivant} + q \ cdot \ sum x_i q ^ i} {1 + q \ cdot \ sum q ^ i} = (1-q) \ cdot \ left [x_ {suivant} + q \ cdot \ sum x_i q ^ i \ right] \\ \ mathrm {EMA} _ {next} = (1-q) \ cdot x_ {next} + q \ cdot \ mathrm {EMA} _ {curr}$$

En conséquence, nous devons choisir une valeur $$$\ alpha = 1-q$ comme constante de lissage. On peut montrer que si vous prenez $$$\ alpha = 2 / (N + 1)$ le centre de masse des poids EMA et SMA ci-dessus devient le même. Dans le code, tout semble beaucoup plus facile.

 function ema($close, window, weight = null) { weight = weight ? weight : 2 / (window + 1); let ema = [ mean($close.slice(0, window)) ]; for (let i = 1; i < $close.length; i++) { ema.push($close[i] * weight + ema[i - 1] * (1 - weight)); }; return ema; } 

En général, il s'agit de la même moyenne mobile, mais plus sensible.



L'efficacité de l'utilisation dépend de votre expérience et des paramètres utilisés. Par exemple, sur ce site les paramètres sont assez bien choisis.

Convergence / divergence moyenne mobile (MACD)

En 1979, Gerald Appel a proposé l'un des oscillateurs de prix les plus simples et les plus efficaces. Il convertit deux indicateurs de tendance EMA en un indicateur de moment, tirant le meilleur de deux mondes. Autrement dit, il, en gros, trouve un dérivé. Il est dessiné dans une fenêtre séparée avec deux lignes et un histogramme, et non superposé, comme les précédents. En fait, il y a beaucoup plus d'indicateurs qui sont dessinés dans une fenêtre distincte, mais cela peut être à un autre moment.



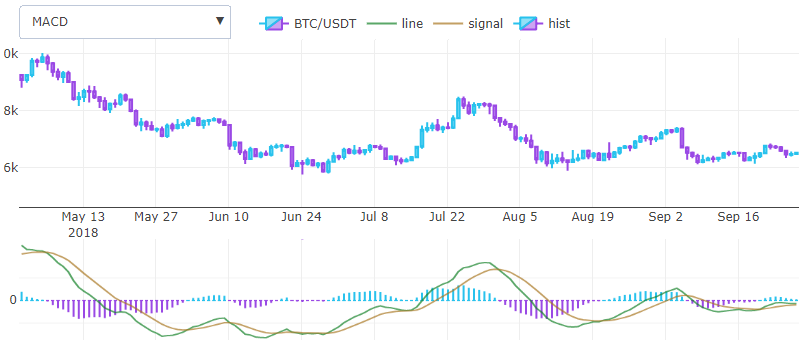
La formule de calcul est assez simple, prenez deux ema avec une fenêtre courte et courte, par exemple, 26 et 12 unités, et soustrait, la ligne résultante sera l'indicateur souhaité. En prenant un autre ema de cette différence avec un pas de 3 unités, nous obtenons une ligne de signal. L'histogramme que Gerald a ajouté plus tard est calculé par la différence entre les deux résultats précédents et est essentiellement une dérivée moyenne pondérée.

 function macd($close, wshort, wlong, wsig) { let line = pointwise((a, b) => a - b, ema($close, wshort), ema($close, wlong)); let signal = ema(line, wsig); let hist = pointwise((a, b) => a - b, line, signal); return { line : line, signal : signal, hist : hist }; } 

Test d'indicateur, erreur standard normalisée

Ayant des tableaux précis avec la signification des indicateurs, vous pouvez tester qualitativement votre calcul. Il existe différentes manières de déterminer la mesure d'erreur entre deux fonctions, mais la pratique a montré que l'erreur quadratique moyenne normalisée, qui est considérée comme

$$

$$\ mathrm {NRMSE} = \ gauche. \ sqrt {\ frac {\ sum (\ hat x_i - x_i) ^ 2} {N}} \ middle / (\ max {x_i} - \ min {x_i}) \ right.$$

fonctionne mieux pour les petites et grandes tailles. Par exemple, le bitcoin en dollars peut coûter 20 000 $ et la différence de 10 $ n'est pas critique, en même temps, un altcoin peut être calculé en plusieurs satoshi.

 function nrmse(f, g) { let sqrDiff = pointwise((a, b) => (a - b) * (a - b), f, g); return Math.sqrt(mean(sqrDiff)) / (Math.max(...f) - Math.min(...f)); } 

Conclusion

Donc en quelques lignes vous pouvez exprimer les indicateurs de base, si vous prévoyez d'effectuer leur analyse par machine learning, puis pour déterminer les points d'entrée idéaux, je vous conseille de faire attention à l'indicateur ZigZag, qui n'est pas utile pour le trading, mais extrêmement utile en tant qu'enseignant. Il convient également de garder à l'esprit que pour le trading, vous devez choisir les indicateurs les plus différents et essayer de modifier leurs paramètres d'entrée. Vous pouvez essayer de les modifier automatiquement au fil du temps, car les paramètres les plus efficaces ont tendance à changer.

Sources utilisées

1. StockCharts - liste d'algorithmes avec des données de vérification dans des tableaux
2. Cryptowatch - paramètres d'indicateur bien réglés
3. Github - code source