Pour éviter d'être détectés par les radars ennemis, les chasseurs, navires et missiles modernes devraient avoir la plus petite zone de dispersion effective (EPR). Les scientifiques et les ingénieurs développant de tels objets discrets, en utilisant des méthodes d'électrodynamique informatique, optimisent l'EPR et les effets de diffusion d'objets arbitraires lors de l'utilisation de radars. L'objet en question disperse les ondes électromagnétiques qui y sont incidentes dans toutes les directions, et une partie de l'énergie retournée à la source d'ondes électromagnétiques dans le processus de ce qu'on appelle la rétrodiffusion, forme une sorte d '"écho" de l'objet. L'EPR n'est qu'une mesure de l'intensité d'un signal d'écho radar.

En pratique, une sphère conductrice de référence est utilisée comme objet pour calibrer les radars. Une formulation similaire du problème est utilisée pour vérifier le calcul numérique de l'EPR, puisque la solution à ce problème classique d'électrodynamique a été obtenue par Gustav Mi en 1908 .

Dans cette note, nous parlerons de la conduite d'un tel calcul de référence en utilisant une formulation axisymétrique bidimensionnelle efficace, et noterons brièvement les principes généraux pour résoudre une large classe de problèmes de diffusion dans COMSOL Multiphysics ^® .

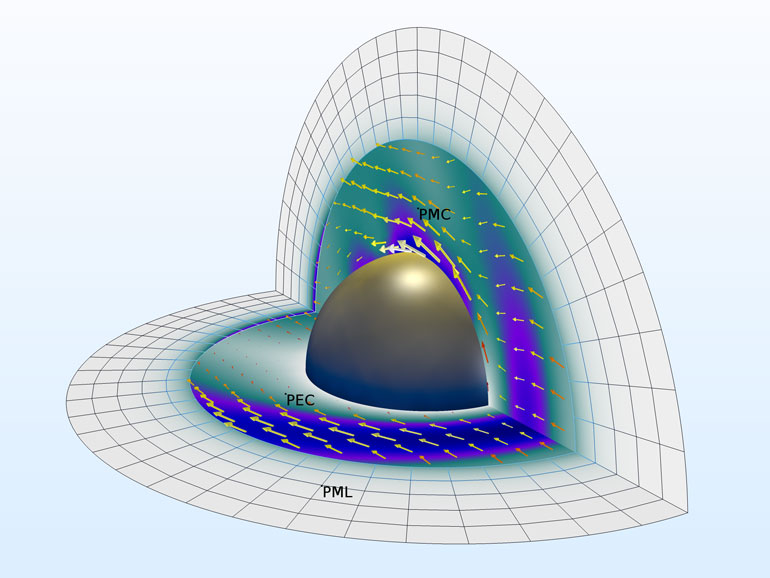
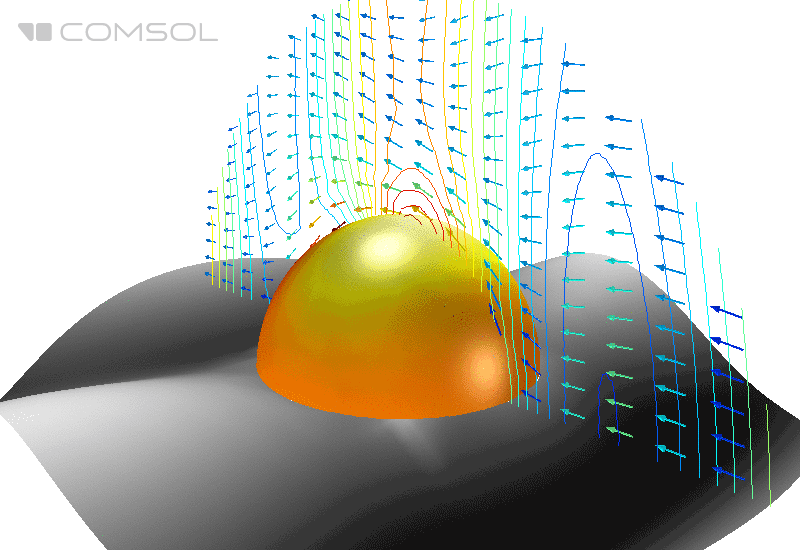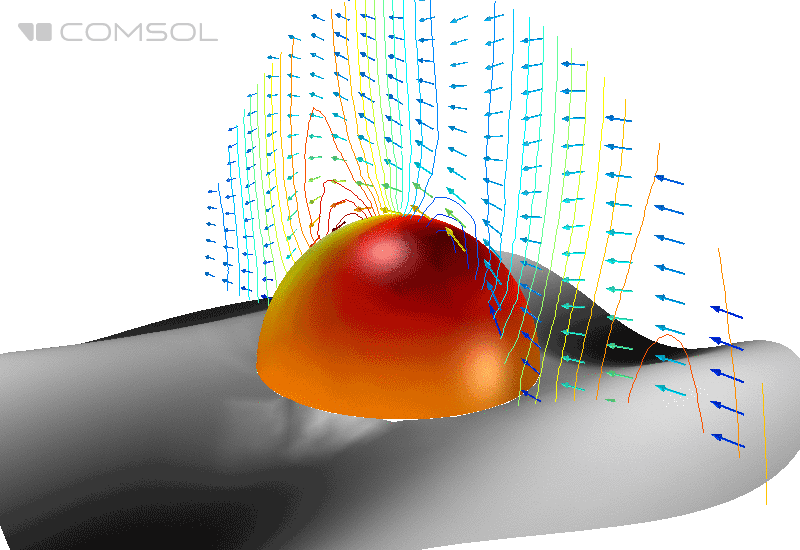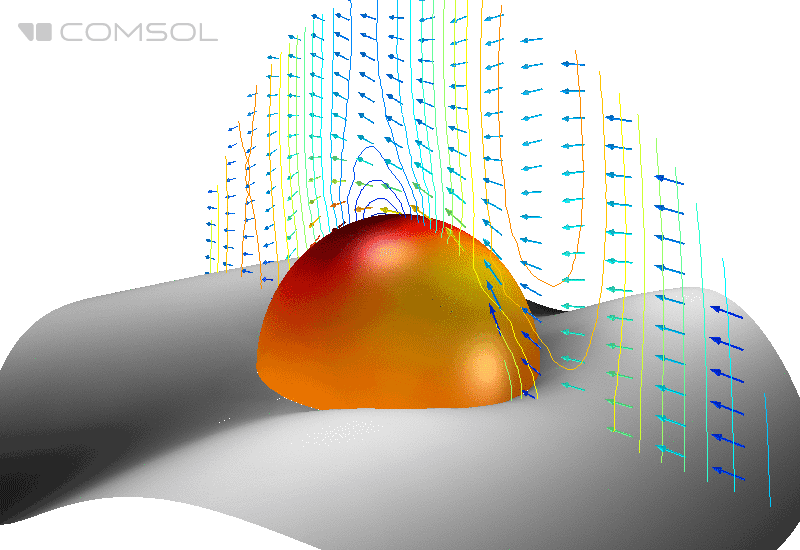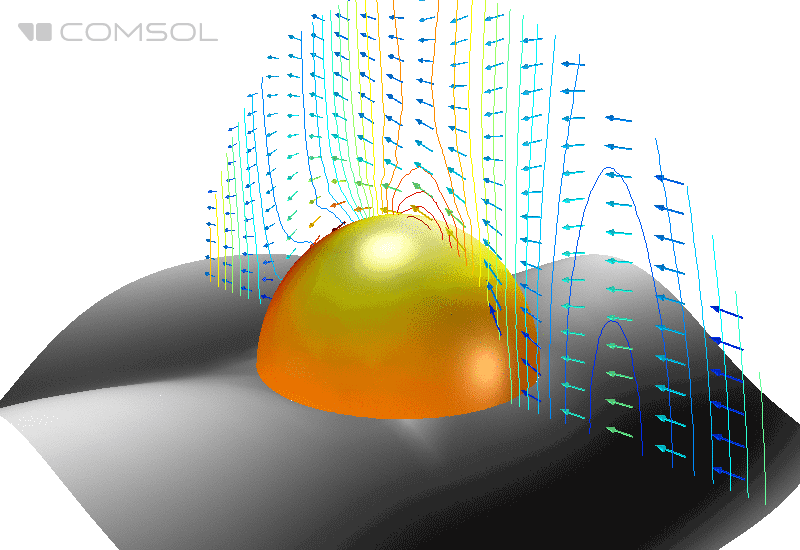
Fig.1. Distribution du champ électrique (sa norme) et du flux d'énergie moyenné dans le temps (flèches) autour d'une sphère parfaitement conductrice dans l'espace libre.

La diffusion de sphères: la taille compte

Dans l' exemple de référence classique , une sphère métallique parfaitement conductrice dans l'espace libre est irradiée avec une onde électromagnétique plane et l'EPR est calculé.

En sortie, la diffusion est généralement calculée pour différents rapports du rayon de la sphère et de la longueur d'onde, sur la base desquels trois zones sont distinguées: les bandes Mi de Rayleigh , optiques et de transition.

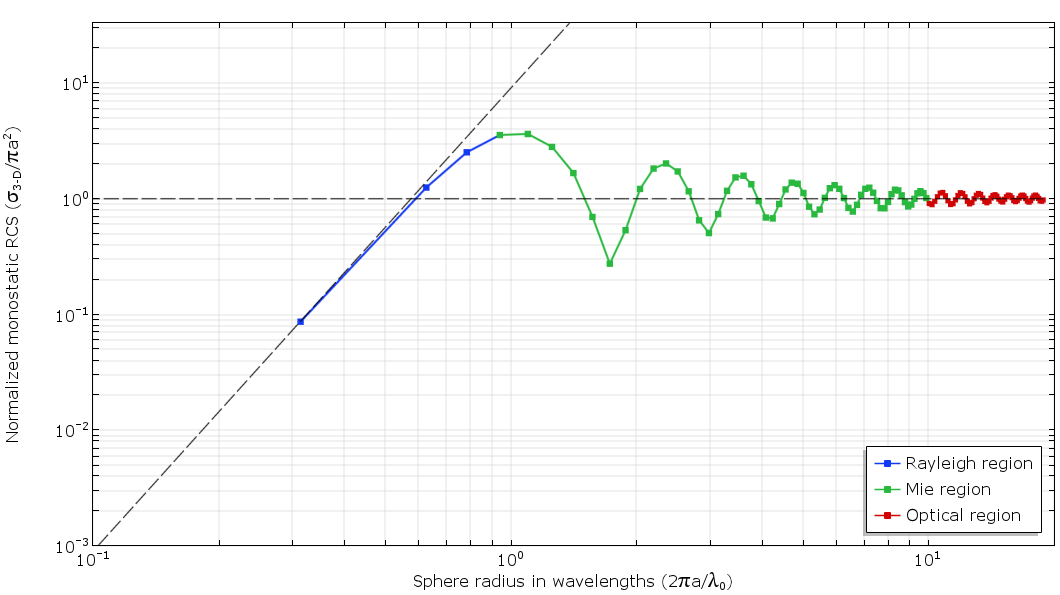
Fig. 2. Un graphique de la dépendance de l'EPR à la longueur d'onde (sur une double échelle logarithmique). Trois domaines caractéristiques sont distingués: Rayleigh, Mi et optique. Les lignes pointillées noires montrent des solutions asymptotiques pour les zones de Rayleigh et optiques.

Les caractéristiques de l'EPR sont considérablement affectées par la taille électrique et les propriétés des matériaux de l'objet sur lequel le faisceau radar est incident. Étant donné que la taille électrique de l'objet - dans notre cas, la sphère - diminue lors du passage de la plage optique à la région de Rayleigh (à travers la bande M), les méthodes asymptotiques ne fourniront pas une précision suffisante pour prendre en compte la contribution de tous les phénomènes physiques. Pour obtenir des résultats précis, le problème doit être résolu en utilisant des techniques pleine onde .

Dans un cadre tridimensionnel, même en tenant compte de l'utilisation de couches parfaitement adaptées (Perfectly Matched Layers - PML), qui limitent efficacement le domaine de calcul et simulent des frontières ouvertes et des conditions de symétrie, un calcul avec une résolution détaillée en fréquence / longueur d'onde peut prendre un certain temps.

Définition des conditions de symétrie pour les calculs électrodynamiques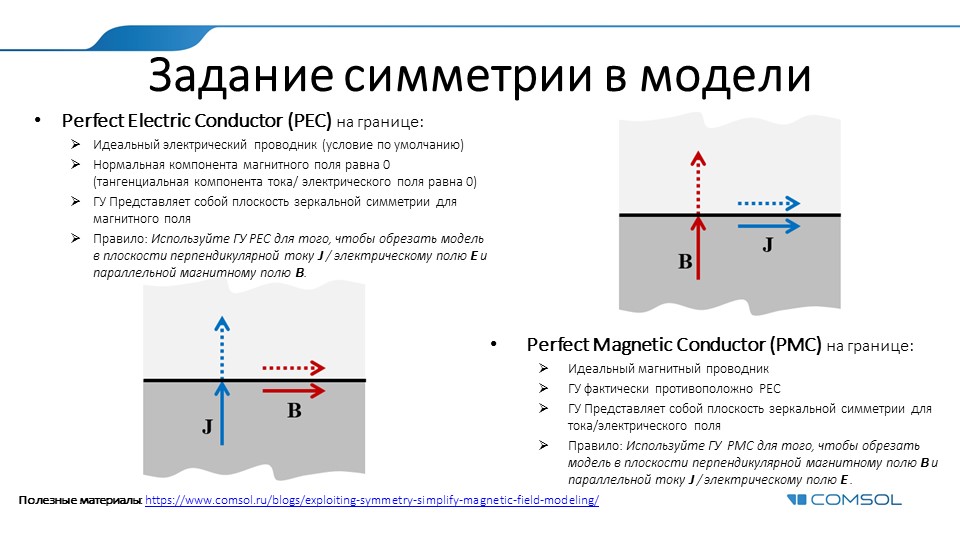

Plus de détails ici .

Heureusement, si l'objet est axisymétrique et diffuse les ondes de manière isotrope, une analyse 3D complète n'est pas requise. Pour analyser la propagation des ondes électromagnétiques et le comportement résonant d'un objet, il suffit de calculer sa section efficace dans une formulation axisymétrique bidimensionnelle sous certaines conditions.

Modèle axisymétrique bidimensionnel du processus micro-ondes: un regard intérieur

Supposons que notre sphère soit métallique et ait une conductivité élevée. Pour cette tâche, la surface de la sphère est définie comme le conducteur électrique parfait (Perfect electric conductor - PEC), et sa partie intérieure est exclue de la zone de calcul. La région qui l'entoure est définie comme un vide avec les propriétés matérielles correspondantes, et le PML sphérique est utilisé dans la couche la plus externe, qui est utilisée pour absorber toutes les ondes sortantes et empêcher la réflexion des limites du domaine de calcul.

Modélisation d'objets métalliques dans les problèmes électromagnétiques des vagues

Pour la solution numérique des problèmes d'électrodynamique dans le domaine fréquentiel, il existe plusieurs méthodes de modélisation efficace des objets métalliques. L'illustration ci-dessous reflète les techniques et recommandations d'utilisation des conditions de transition aux limites (TBC), des conditions aux limites d'impédance (IBC) et des conditions Perfect Electric Conductor (PEC).

Une analyse détaillée des aspects d'application de chacun d'eux est ici .

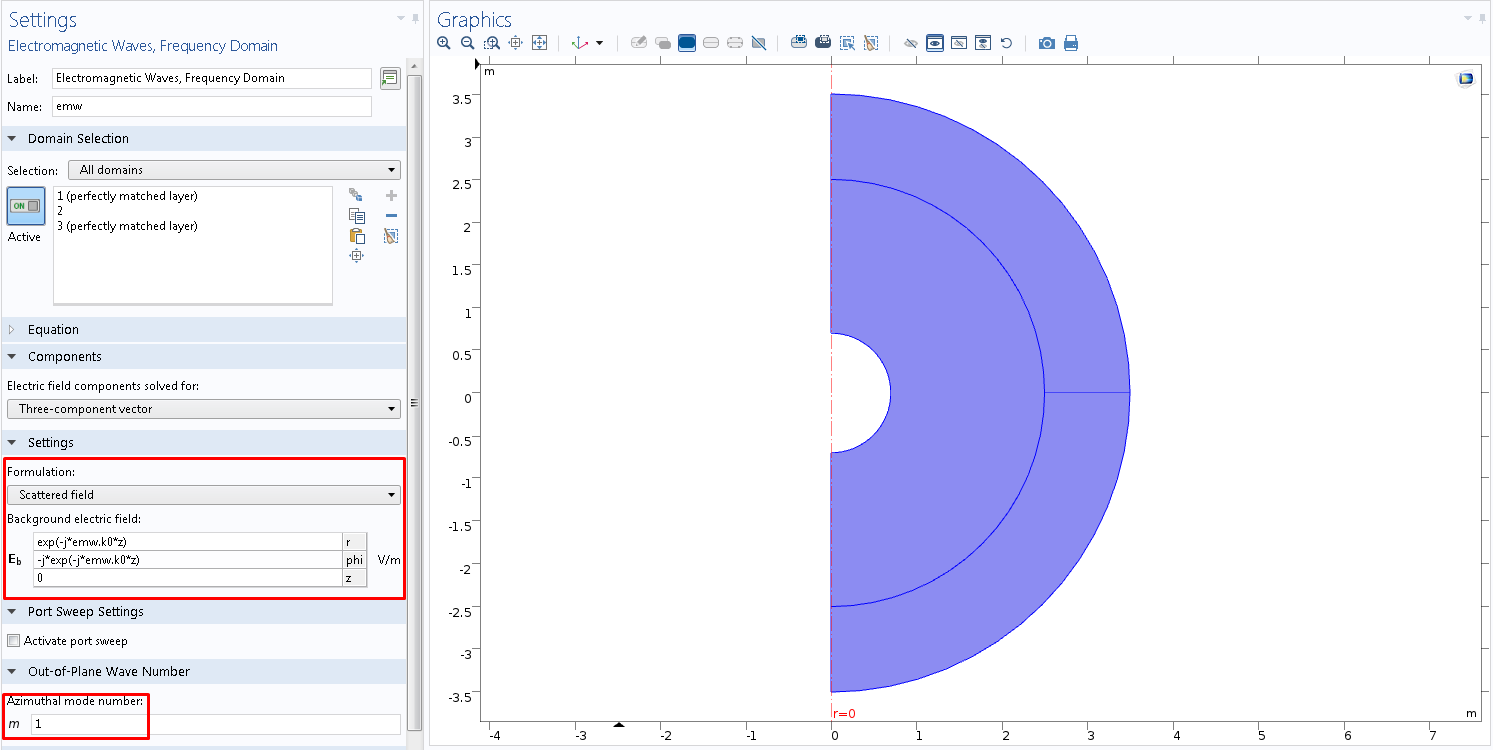
Fig. 3. Géométrie pour la formulation axisymétrique et définition du champ électromagnétique de fond avec polarisation circulaire gauche dans l'interface graphique COMSOL Multiphysics ^® .

Dans le domaine informatique (sauf pour PML), l'excitation du champ de fond avec la polarisation circulaire gauche dirigée dans la direction négative de l'axe z est spécifiée (Fig. 3). Veuillez noter que le calcul est défini uniquement pour le premier mode azimutal.

Par défaut, pour les tâches micro-ondes dans COMSOL Multiphysics ^{®, une} grille triangulaire gratuite (ou tétraédrique pour les problèmes 3D) est automatiquement construite pour la fréquence maximale spécifiée pour l'étude dans le domaine fréquentiel (étude du domaine fréquentiel), qui dans cet exemple est de 200 MHz. Pour garantir une résolution suffisante des processus ondulatoires dans le modèle, la taille maximale de l'élément de maillage est définie égale à 0,2 longueur d'onde. En d'autres termes, la résolution spatiale est spécifiée comme cinq éléments de second ordre par longueur d'onde. Dans des couches parfaitement adaptées, la grille est construite en tirant dans le sens de l'absorption, ce qui garantit des performances PML maximales.

Parce que Le nombre de degrés de liberté dans le modèle étant très faible (par rapport à la formulation tridimensionnelle), son calcul ne prend que quelques secondes. En sortie, l'utilisateur peut obtenir et visualiser la répartition du champ électrique autour de la sphère (dans la zone proche), qui est la somme du fond et des champs diffusés.

Pour cette tâche, les caractéristiques les plus intéressantes concernent la région du champ lointain. Pour les intégrer dans le modèle, vous devez activer la condition de calcul de champ lointain à la limite extérieure du domaine de calcul (dans ce cas, la frontière PML intérieure), qui vous permet de calculer les champs dans la zone éloignée en dehors du domaine de calcul à tout moment en fonction des relations intégrales Stratton-Chu. L'activation ajoute une variable supplémentaire - l'amplitude du champ dans la zone éloignée, sur la base de laquelle, en post-traitement, le logiciel calcule des variables d'ingénierie conformes aux normes IEEE: puissance isotrope rayonnée efficace, gain (ce que l'on appelle le gain, y compris en tenant compte de l'inadéquation d'entrée), coefficient action directionnelle et EPR.

Selon le graphique polaire, un spécialiste peut déterminer la directivité du champ dans la zone éloignée dans un certain plan, et un diagramme de rayonnement tridimensionnel dans la zone éloignée permet une étude plus détaillée du champ de diffusion (Fig.4).

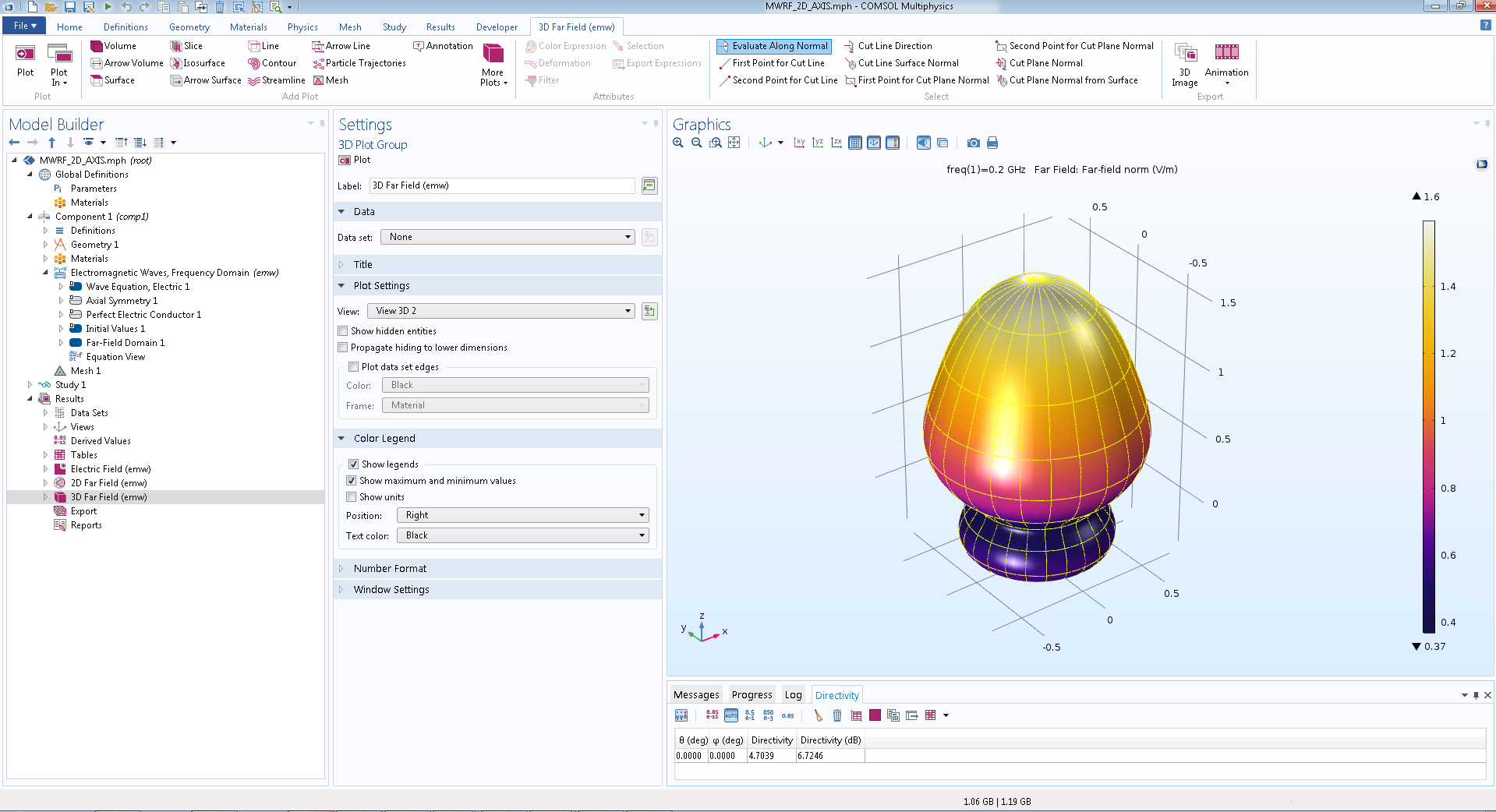
Fig. 4. Visualisation tridimensionnelle du champ dans la zone éloignée basée sur un modèle axisymétrique bidimensionnel dans COMSOL Multiphysics ^® .

Récupération de solution pour un problème en trois dimensions

Les résultats du modèle «raccourci» dans une formulation axisymétrique concernent le processus d'irradiation de la sphère conductrice avec un champ de fond polarisé circulaire. Dans le problème 3D d'origine, les caractéristiques du champ de diffusion sont étudiées dans le cas d'une onde plane polarisée linéairement. Comment contourner cette différence?

Par définition, la polarisation linéaire peut être obtenue en ajoutant la polarisation circulaire droite et gauche. Le modèle axisymétrique bidimensionnel avec les réglages ci-dessus (Fig.2) correspond au premier mode azimutal (m = 1) du champ de fond avec polarisation circulaire gauche. La solution du mode azimutal négatif avec polarisation circulaire droite peut facilement être déduite du problème déjà résolu en utilisant les propriétés de symétrie et en effectuant de simples transformations algébriques.

Après avoir effectué une seule analyse bidimensionnelle et mis en miroir les résultats déjà en cours de post-traitement, vous pouvez extraire toutes les données nécessaires, en économisant de manière significative les ressources de calcul (Fig. 5).

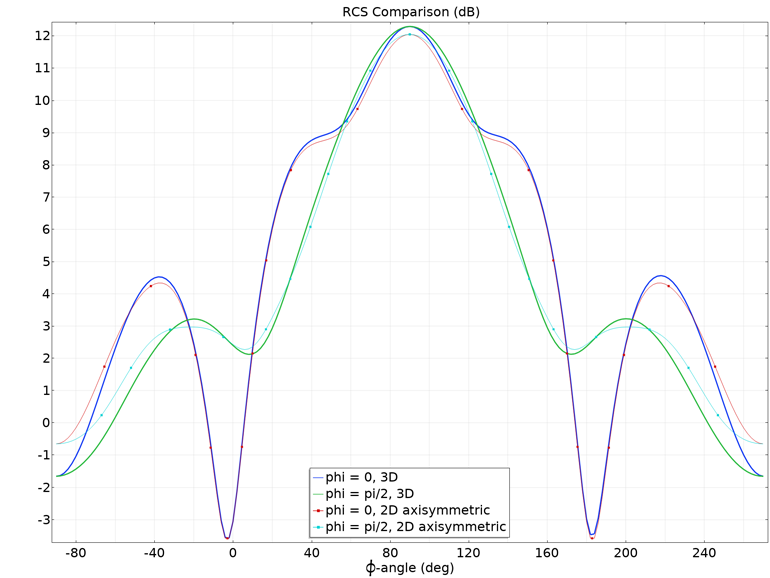
Fig. 5. Comparaison du balayage de la zone de diffusion effective (sur une échelle logarithmique) sur des angles de diffusion pour un calcul tridimensionnel complet et le modèle axisymétrique bidimensionnel proposé.

Le graphique unidimensionnel (Fig. 5) avec une comparaison EPR démontre une correspondance acceptable entre les modèles axisymétriques tridimensionnels et bidimensionnels. Une légère différence n'est observée que dans la région de diffusion avant et arrière, près de l'axe de rotation.

De plus, pour la visualisation des résultats bidimensionnels obtenus dans l'espace tridimensionnel, une transformation du système de coordonnées de cylindrique en cartésien sera nécessaire. Dans la fig. La figure 6 montre une visualisation tridimensionnelle des résultats pour un modèle axisymétrique bidimensionnel.

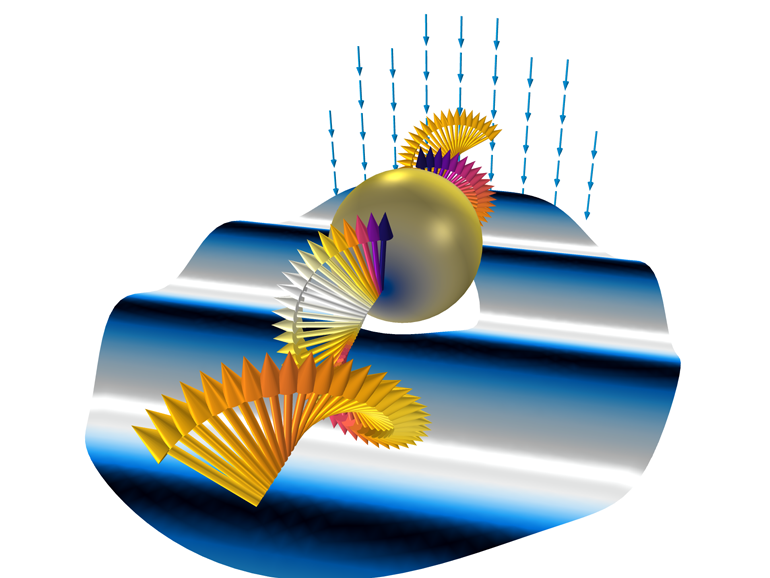
Fig. 6. Présentation tridimensionnelle des résultats basée sur un calcul bidimensionnel.

Les flèches tournant en spirale indiquent un champ de fond avec une polarisation circulaire. Le graphique dans la section horizontale représente la distribution de la composante radiale du champ d'arrière-plan (le processus d'onde est affiché en utilisant les déformations du plan). La norme du champ électrique total est construite à la surface de la sphère. Un autre diagramme en flèche montre une superposition de deux polarisations circulaires, ce qui équivaut à un champ de fond avec une polarisation linéaire dans un espace tridimensionnel.

Conclusion

Dans le processus de développement moderne dans le domaine de la radiophysique et de la technologie des micro-ondes pour les ingénieurs, les techniques de modélisation efficaces qui réduisent la consommation de ressources et le temps sont irremplaçables quelle que soit la méthode d'analyse numérique appliquée.

Pour maintenir l'intégrité et recréer tous les effets physiques pertinents lors de la modélisation d'un composant réel avec une grande taille électrique, il est possible de simplifier le processus de calcul numérique sans perte de précision en résolvant le problème dans une formulation axisymétrique bidimensionnelle. Lors de la modélisation et de l'analyse d'objets axisymétriques tels que des sphères et des disques de diffusion, des cornes coniques et des antennes paraboliques , les calculs de la section efficace de l'appareil sont effectués plusieurs ordres de grandeur plus rapidement que lors de l'utilisation du modèle tridimensionnel complet.

Bases de la modélisation d'antenne dans COMSOL Multiphysics

Une courte revue vidéo (en russe) , qui montre des exemples de modélisation d'antennes micro-ondes à l'aide du module Radio Frequency, y compris le calcul des caractéristiques de fréquence des paramètres S et de l'impédance, des diagrammes de Smith, des études d'appariement, le calcul de champs dans la zone éloignée, la détermination du coefficient de directivité (Directivité) et gagner (Gain). De plus, les principes d'utilisation de la symétrie, de modélisation d'antennes en réception et de calculs complexes de systèmes de récepteurs et d'émetteurs espacés dans l'espace, d'évaluation des interférences électromagnétiques sur les antennes voisines, et bien plus encore, sont pris en compte.

Dans ce cas, une formulation bidimensionnelle simple permet de reconstruire rapidement en espace tridimensionnel et d'étudier la diffusion du champ de fond avec polarisation linéaire, ainsi que la directivité du rayonnement dans la zone lointaine pour les antennes excitées par le guide d'onde circulaire TE11 transverse.

Information additionnelle

Ce matériel est basé sur un article de J. Munn. Analyse numérique rapide de la diffusion et de la section efficace du radar , micro-ondes et RF 3 mai 2018

La fonctionnalité COMSOL Multiphsycics ^® vous permet également de simuler:

• Radars de forme libre et radars
• Diffusion à large bande basée sur la technique DG-FEM (formulation dans le domaine temporel utilisant des solveurs explicites et conversion FFT ultérieure)
• Diffusion par des objets 3D, notamment par une nanoparticule placée sur un substrat diélectrique .

Pour une connaissance plus détaillée des capacités de notre package pour les applications considérées dans cet article, nous vous invitons à participer à notre nouveau webinaire "Solution des problèmes de diffusion dans COMSOL Multiphsycics ^® " , qui se tiendra le 22 août 2018.

Vous pouvez également demander une version de démonstration de COMSOL dans les commentaires ou sur notre site Web .

GIF final: