Méthodes numériques pour résoudre des systèmes d'équations non linéaires

Présentation

De nombreux problèmes appliqués obligent à trouver une solution générale à un système d'équations non linéaires. Aucune solution analytique générale du système d'équations non linéaires n'a été trouvée. Il n'y a que des méthodes numériques.

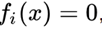
Il convient de noter un fait intéressant que tout système d'équations sur des nombres réels peut être représenté par une équation équivalente, si nous prenons toutes les équations sous la forme , placez-les et pliez-les.

Pour la solution numérique, des méthodes itératives d'approximations successives (itération simple) et la méthode de Newton dans diverses modifications sont utilisées. Les processus itératifs sont naturellement généralisés au cas d'un système d'équations non linéaires de la forme:

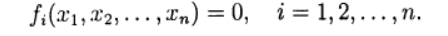
(1)

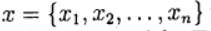
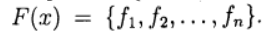
Désigner par vecteur d'inconnues et définir une fonction vectorielle Le système (1) s'écrit alors sous la forme de l'équation:

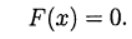
(2)

Maintenant, revenons à notre Python bien-aimé et notons sa primauté parmi les langages de programmation qui veulent apprendre [1].



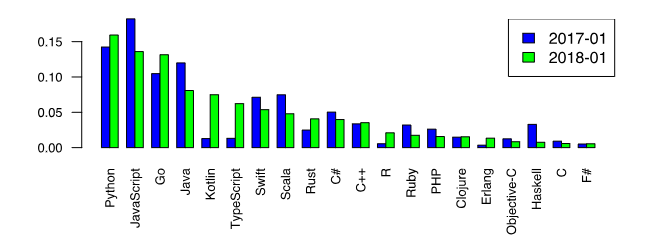
Ce fait est une incitation supplémentaire à considérer les méthodes numériques en Python. Cependant, les amateurs de Python estiment que les fonctions de bibliothèque spéciales, telles que scipy.optimize.root, spsolve_trianular, newton_krylov , sont le meilleur choix pour résoudre les problèmes par des méthodes numériques.

Il est difficile d'être en désaccord avec cela, ne serait-ce que parce que la variété des modules a également élevé Python au sommet de la popularité. Cependant, il existe des cas où, même avec un examen superficiel, l'utilisation de méthodes connues directes sans utiliser les fonctions spéciales de la bibliothèque SciPy donne également de bons résultats. En d'autres termes, le nouveau est l'ancien bien oublié.

Ainsi, dans la publication [2], basée sur les expériences de calcul effectuées, il a été prouvé que la fonction de bibliothèque newton_krylov, conçue pour résoudre de grands systèmes d'équations non linéaires, a la moitié de la vitesse que l'algorithme TSLS + WD
(moindres carrés en deux étapes) implémenté par la bibliothèque NumPy.

Le but de cette publication est de comparer le nombre d'itérations, la vitesse et, surtout, le résultat de la résolution d'un problème de modèle sous la forme d'un système de cent équations algébriques non linéaires à l'aide de la fonction de bibliothèque scipy.optimize.root et de la méthode de Newton implémentée à l'aide de la bibliothèque NumPy.

Capacités du solveur Scipy.optimize.root pour la résolution numérique de systèmes d'équations non linéaires algébriques

La fonction de bibliothèque scipy.optimize.root a été choisie comme base de comparaison car elle possède une vaste bibliothèque de méthodes adaptées à l'analyse comparative.

scipy.optimize.root ( fun, x0, args = (), method = 'hybr', jac = None, tol = None, callback = None, ptions = None )
fun - Une fonction vectorielle pour trouver la racine.
x0 est la condition initiale de la recherche de racines

méthode:
hybr - modification Powell de la méthode hybride est utilisée;
lm - résout des systèmes d'équations non linéaires en utilisant la méthode des moindres carrés.
Comme il ressort de la documentation [3], les méthodes broyden1, broyden2, anderson, linearmixing, diagbroyden, passionmixing, krylov sont les méthodes exactes de Newton. Les paramètres restants sont «facultatifs» et peuvent être trouvés dans la documentation.

Méthodes de résolution de systèmes d'équations non linéaires

Le matériel donné ci-dessous peut en effet être lu dans la littérature, par exemple, dans [4], mais je respecte mon lecteur et, pour sa commodité, je présente la dérivation de la méthode sous une forme abrégée, si possible. Ceux qui n'aiment pas les formules sautent cette section.

Dans la méthode de Newton, une nouvelle approximation pour résoudre le système d'équations (2) est déterminée à partir de la solution du système d'équations linéaires :

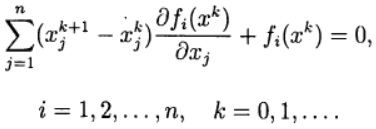
(3)

Définissez la matrice de Jacobi:

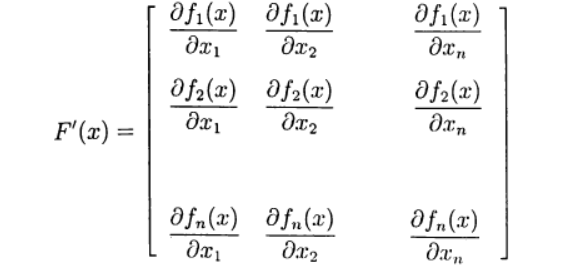
(4)

Nous écrivons (3) sous la forme:

(5)

De nombreuses méthodes en une étape pour une solution approximative de (2) par analogie avec des méthodes itératives à deux couches pour résoudre des systèmes d'équations algébriques linéaires peuvent être écrites sous la forme:

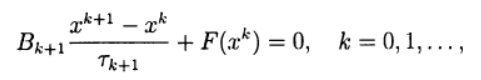
(6)

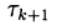
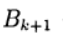
où Les paramètres itératifs sont-ils - une matrice carrée n x n ayant l'inverse.

Lors de l'utilisation de l'enregistrement (6), la méthode de Newton (5) correspond au choix:



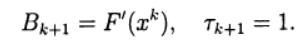
Le système d'équations linéaires (5) pour trouver une nouvelle approximation peut être résolu de manière itérative. Dans ce cas, nous avons un processus itératif en deux étapes avec des itérations externes et internes. Par exemple, un processus itératif externe peut être effectué selon la méthode de Newton, et des itérations internes peuvent être effectuées sur la base de la méthode itérative Seidel.

Lors de la résolution de systèmes d'équations non linéaires, on peut utiliser des analogues directs des méthodes itératives standard utilisées pour résoudre des systèmes d'équations linéaires. La méthode non linéaire de Seidel appliquée à la solution (2) donne:

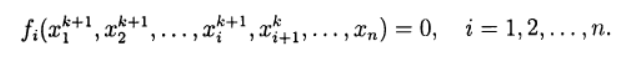
(7)

Dans ce cas, chaque composante de la nouvelle approximation à partir de la solution de l'équation non linéaire peut être obtenue sur la base de la méthode d'itération simple et de la méthode de Newton dans diverses modifications. Ainsi, nous arrivons à nouveau à une méthode itérative en deux étapes dans laquelle les itérations externes sont effectuées conformément à la méthode Seidel, et les itérations internes sont effectuées en utilisant la méthode Newton.

Les principales difficultés de calcul dans l'application de la méthode de Newton pour la solution approximative de systèmes d'équations non linéaires sont liées à la nécessité de résoudre un système d'équations linéaire avec une matrice de Jacobi à chaque itération , et cette matrice change d'itération en itération. Dans la méthode de Newton modifiée, la matrice de Jacobi n'est inversée qu'une seule fois:

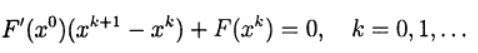
(8)

Sélection de la fonction du modèle

Un tel choix n'est pas une tâche simple, car avec une augmentation du nombre d'équations dans le système en fonction d'une augmentation du nombre de variables, le résultat de la solution ne devrait pas changer, car sinon il est impossible de suivre l'exactitude de la solution du système d'équations lors de la comparaison de deux méthodes. J'apporte la solution suivante pour la fonction modèle:

n=100 def f(x): f = zeros([n]) for i in arange(0,n-1,1): f[i] = (3 + 2*x[i])*x[i] - x[i-1] - 2*x[i+1] - 2 f [0] = (3 + 2*x[0] )*x[0] - 2*x[1] - 3 f[n-1] = (3 + 2*x[n-1] )*x[n-1] - x[n-2] - 4 return f 

La fonction f crée un système de n équations non linéaires, dont la solution ne dépend pas du nombre d'équations et est égale à l'unité pour chacune des n variables.

Un programme pour tester une fonction de modèle avec les résultats de la résolution d'un système d'équations non linéaires algébriques en utilisant la fonction de bibliothèque Optimize.root pour différentes méthodes de recherche de racines

 from numpy import* from scipy import optimize import time ti = time.clock() n=100 def f(x): f = zeros([n]) for i in arange(0,n-1,1): f[i] = (3 + 2*x[i])*x[i] - x[i-1] - 2*x[i+1] - 2 f [0] = (3 + 2*x[0] )*x[0] - 2*x[1] - 3 f[n-1] = (3 + 2*x[n-1] )*x[n-1] - x[n-2] - 4 return f x0 =zeros([n]) sol = optimize.root(f,x0, method='krylov') print('Solution:\n', sol.x) print('Krylov method iteration = ',sol.nit) print('Optimize root time', round(time.clock()-ti,3), 'seconds') 

Seule l' une des méthodes décrites dans les documents [3] a passé le test par le résultat de la fonction de modèle de décision, cette méthode 'Krylov.

Solution pour n = 100:

Solution:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1.]
Itération de la méthode de Krylov = 4219
Optimiser le temps root 7,239 secondes:


Conclusion: Avec une augmentation du nombre d'équations de moitié, l'apparition d'erreurs dans la solution est perceptible. Avec une nouvelle augmentation de n, la solution devient inacceptable, ce qui est possible du fait de l'adaptation automatique à l'étape, même raison d'une forte baisse des performances. Mais c'est juste ma supposition.

Un programme pour tester une fonction de modèle avec les résultats de la résolution d'un système d'équations algébriques non linéaires en utilisant un programme écrit en Python 3 en tenant compte des relations (1) - (8) pour trouver les racines en utilisant la méthode de Newton modifiée

Solution pour n = 100:

Solution:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1.]
Itération de Newton = 13
Temps de la méthode de Newton 0,496 seconde

Solution pour n = 200:

Solution:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
Itération de Newton = 14
Temps de la méthode de Newton 1.869 secondes

Pour vous assurer que le programme résout vraiment le système, nous réécrivons la fonction modèle pour éviter la racine avec une valeur de 1 sous la forme:

 n=10 def f(x): f = zeros([n]) for i in arange(0,n-1,1): f[i] = (3 + 2*x[i])*x[i]*sin([i]) - x[i-1] - 2*x[i+1] - 2+e**-x[i] f [0] = (3 + 2*x[0] )*x[0] - 2*x[1] - 3 f[n-1] = (3 + 2*x[n-1] )*x[n-1] - x[n-2] - 4 return f 

Nous obtenons:
Solution:
[0,96472166 0,87777036 0,48175823 -0,26190496 -0,63693762 0,49232062
-1,31649896 0,6865098 0,89609091 0,98509235]
Itération de Newton = 16
Temps de la méthode de Newton 0,046 seconde

Conclusion: Le programme fonctionne également lorsque la fonction de modèle change.

Maintenant, nous revenons à la fonction de modèle initiale et vérifions une plage plus large pour n, par exemple, à 2 et 500.
n = 2
Solution:
[1. 1.]
Itération de Newton = 6
Temps de la méthode de Newton 0,048 seconde
n = 500

Conclusions:

Un programme écrit en Python utilisant la méthode de Newton modifiée, lors de la résolution de systèmes d'équations non linéaires à partir de la fonction de modèle donnée, a plus de stabilité de solution que lors de la résolution en utilisant la fonction de bibliothèque Optimize.root (f, x0, method = 'krylov') pour la méthode Krylov. En ce qui concerne la vitesse de la conclusion finale, il est impossible de tirer en raison de l'approche différente du contrôle de pas.

Références:

1. Évaluation des langages de programmation 2018.
2. Cooper I.V., Faleychik B.V. Processus itératifs non matriciels avec suppression d'erreur quadratique moyenne pour les grands systèmes d'équations non linéaires.
3. scipy.optimize.root.
4. Vabishchevich P.N. Méthodes numériques: Atelier informatique. - M.: Maison du livre "LIBROCOM", 2010. - 320 p.