Bonne journée à tous!
Nous continuons à considérer les possibilités de la mécanique quantique pour transmettre des informations en utilisant la corrélation des particules enchevêtrées quantiques. Contrairement aux méthodes de communication classiques, l'utilisation de particules quantiques enchevêtrées offre la possibilité de transmettre instantanément des informations sur de longues distances. La difficulté réside dans la recherche de moyens pour encoder et décoder les informations transmises. Cet article est consacré à la recherche de solutions à ce problème et à la possibilité de créer une configuration expérimentale. Si vous êtes également intéressé par cette tâche - bienvenue au chat!
Permettez-moi de vous rappeler que
dans le dernier article, nous avons considéré l'un des schémas possibles de transmission d'informations entre deux objets distants. En particulier, un schéma optique avec séparateurs de faisceau pour obtenir des interférences a été envisagé, ainsi qu'un schéma de détection et d'effacement quantique utilisant deux convertisseurs abaisseurs. Dans les commentaires, il y a eu beaucoup de discussions sur l'opérabilité d'un tel schéma, ainsi que des critiques de la part de l'utilisateur selon lesquelles l'utilisation de convertisseurs abaisseurs entraîne une interaction avec la particule source, un décalage de phase du motif d'interférence et d'autres conséquences désagréables. Je n'exclue pas cette possibilité, par conséquent, après un examen détaillé, j'ai décidé d'exclure l'utilisation de convertisseurs abaisseurs et de construire un circuit utilisant des polariseurs circulaires et linéaires. Pour l'avenir, je peux dire que cette solution a ses propres difficultés, en raison desquelles il est impossible d'avoir une image des interférences. Pour résoudre ces difficultés, nous utiliserons l'approche élégante résultant des conséquences de la mécanique quantique elle-même. Je suis profondément reconnaissant à tous ceux qui ont participé à la discussion du dernier article. Vos arguments et critiques m'ont aidé à mieux comprendre les difficultés rencontrées, à rechercher plus d'informations et à trouver de nouvelles solutions.
Pour commencer, envisagez une
véritable configuration expérimentale . Le faisceau laser frappe un dispositif optique non linéaire: un cristal de bêta-borate de baryum (BBO), grâce auquel un photon est converti en deux photons de basse fréquence intriqués. Un processus connu sous le nom de diffusion paramétrique spontanée. La paire de photons résultante suit différents chemins, dont l'un va directement au
détecteur 1 , et le second passe par une double fente et entre dans le
détecteur 2 . Les deux détecteurs sont connectés au circuit de coïncidence, garantissant que seules les paires de photons enchevêtrées sont prises en compte. Un moteur pas à pas déplace le deuxième détecteur et balaye la zone cible, créant une carte d'intensité qui forme un motif d'interférence familier.
Pour un photon passant par une double fente, des polariseurs circulaires sont placés devant chaque fente, créant une polarisation de la lumière dans le sens horaire lors du passage dans une fente, et une polarisation dans le sens antihoraire lors du passage dans une autre fente. Les photons qui traversent le polariseur dans le sens horaire ne peuvent pas traverser le polariseur dans le sens antihoraire. Et les photons passant à travers le polariseur dans le sens antihoraire, respectivement, ne peuvent pas traverser le polariseur dans le sens horaire. Les polariseurs circulaires «étiquettent» les photons, détruisant le motif d'interférence au second détecteur (
lois de Fresnel-Arago ).
Ensuite, un polariseur linéaire est introduit dans le trajet du premier photon, ce qui permet d'obtenir une polarisation diagonale des photons. L'intrication fournit également une polarisation diagonale supplémentaire à son partenaire, qui passe à travers un double espace. Cela change l'effet des polariseurs circulaires - maintenant chaque photon est capable de passer à travers les polariseurs circulaires dans le sens horaire et antihoraire. Ainsi, il n'est plus possible de déterminer le chemin parcouru par les photons et les franges d'interférence sont restaurées.
Considérez cela plus en détail dans l'exemple suivant. Imaginez Alice utilisant une polarisation linéaire ou circulaire sur le premier détecteur, affectant instantanément les résultats de Bob sur le second détecteur. Supposons qu'un cristal BBO produit l'état suivant:
Si Alice place un polariseur circulaire devant un détecteur qui filtre les photons polarisés dans le sens horaire, alors chaque fois qu'Alice mesure un photon, le photon Bob correspondant a nécessairement une polarisation dans le sens horaire:
Puisque Bob a placé des filtres polarisants opposés près de chaque fente, nous savons que ces photons ne peuvent traverser (disons) que la première fente. De cet écart, ils tombent sur l'écran en fonction de la fonction d'onde:
où a est la distance entre les fentes, d est la distance entre les fentes et l'écran, et x est la distance au milieu de l'écran. L'intensité lumineuse sur l'écran (le nombre de photons) sera proportionnelle au carré de l'amplitude de cette onde, autrement dit
De même, quand Alice mesure un photon avec une polarisation dans le sens antihoraire, le photon Bob correspondant est polarisé dans le sens antihoraire, qui ne peut traverser la deuxième fente et apparaître sur l'écran avec une fonction d'onde
Notez que la seule différence est le signe a / 2, car le photon a été émis par une autre fente. Sur l'écran, nous verrons également un point - mais c'est un autre point qui est décalé d'une distance
a . Il y a un point important: si Bob ne découvre jamais quelle polarisation Alice a appliquée, alors Bob voit en fait la somme de deux intensités sur son écran:
car les deux sont produits en quantités égales par le cristal. Bob ne peut distinguer que deux pics dans ses données. Ce n'est qu'après avoir reçu les résultats de la mesure d'Alice qu'il peut voir que pour l'ensemble de photons où Alice a mesuré la polarisation dans le sens des aiguilles d'une montre, le sous-ensemble des photons de Bob a été distribué selon

et pour un ensemble de photons, où Alice mesure la polarisation dans le sens antihoraire, un sous-ensemble des photons de Bob est distribué selon
 (deux pics et leur somme lorsque Alice mesure la polarisation des photons à l'aide d'un polariseur circulaire)
(deux pics et leur somme lorsque Alice mesure la polarisation des photons à l'aide d'un polariseur circulaire)Considérons maintenant la situation où Alice utilisera un polariseur linéaire au lieu d'un polariseur circulaire. La première chose à faire est d'écrire la fonction d'onde du système en termes d'états de polarisation linéaire:
Quand Alice utilise un polariseur horizontal, la fonction d'onde photonique de Bob sera dans un état de superposition de polarisation dans le sens horaire et antihoraire. Cela signifie que le photon peut réellement traverser les deux fentes! Quand on frappe sur l'écran, on obtient l'amplitude de l'onde
et son intensité
où

représente la différence de phase entre deux fonctions d'onde à la position x sur l'écran. Maintenant, l'écran a vraiment une image d'interférence! De même, si Alice utilise un polariseur vertical, alors l'amplitude des ondes photoniques de Bob est
et intensité
Et encore une fois, un motif d'interférence apparaît sur l'écran, mais il a légèrement changé par rapport au précédent en raison de la différence de phase des photons traversant les polariseurs horizontal et vertical.
Alice peut-elle envoyer un message à Bob, encodant son message à l'aide de polariseurs linéaires et circulaires? Malheureusement non. Puisque Bob n'a pas été informé de la polarisation qu'Alice avait utilisée, tout ce qu'il voit est la somme de deux interférences. Par conséquent, le résultat
est encore une tache.
(deux motifs d'interférence et leur somme lorsque Alice mesure la polarisation des photons à l'aide d'un polariseur linéaire)Les corrélations varient selon l'expérience d'Alice. Malgré le fait que l'image globale soit la même, les deux sous-ensembles produisent en fin de compte des corrélations radicalement différentes: si Alice utilise la polarisation linéaire, l'image complète à l'écran est formée de deux modèles d'interférence, et si Alice utilise la polarisation circulaire, l'image est la somme de deux pics.
Pour détecter les interférences, vous devrez modifier cette expérience comme suit: au lieu de deux emplacements avec polariseurs circulaires, il sera nécessaire d'installer un interféromètre Mach Zehnder. Examinons plus en détail le principe de fonctionnement de cet interféromètre et essayons de savoir ce qui change lorsqu'il est utilisé.
INTERFÉROMÈTRE MACH ZENDERÀ l'entrée de l'interféromètre, il y a un miroir translucide qui divise le flux lumineux en deux faisceaux. Réfléchis par deux miroirs opaques, ils sont réunis dans un deuxième miroir translucide. Si le photon était une particule classique, avec une probabilité de 50%, il pourrait passer à travers le premier miroir translucide, et avec une probabilité de 50%, il sera réfléchi par lui.
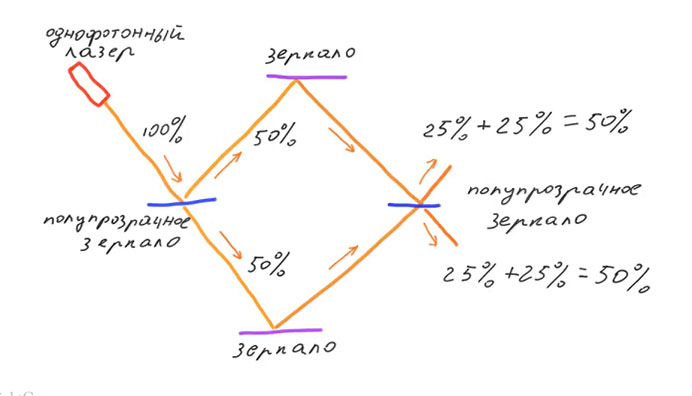
Supposons qu'un photon passe le premier miroir translucide et se déplace le long de la branche inférieure. Sur le deuxième miroir translucide, il peut également passer ou se refléter avec une probabilité de 50%. Autrement dit, la contribution de la branche inférieure est la suivante: 25% du nombre initial de photons se déplacera vers le haut après le deuxième miroir translucide et 25% vers le bas. Si le photon s'est réfléchi sur le premier miroir translucide et est allé le long de la branche supérieure, alors sur le deuxième miroir translucide il peut soit passer, soit être réfléchi. La contribution de la branche supérieure sera également de 25% de haut en bas. La probabilité totale est la somme des contributions de deux branches et est de 50% que le photon se déplacera vers le haut après avoir traversé le deuxième miroir translucide et de 50% vers le bas.
Si nous menons une véritable expérience, nous verrons que tous les photons passant par l'appareil vont descendre. Pas un seul photon ne remontera après le deuxième miroir translucide. Le fait est qu'après avoir passé le premier miroir translucide, un photon sera décrit non pas par des probabilités classiques, mais par une superposition quantique.
Nous désignons par les vecteurs ket de base avec des flèches deux directions possibles du photon: de haut en bas. Dans un premier temps, le photon sera ensuite décrit par le vecteur d'état "down". Après avoir traversé le premier miroir translucide, le photon sera dans une superposition des vecteurs de base haut et bas. Cette superposition est une autre réalisation physique du qubit, avec le spin électronique et la polarisation du photon.
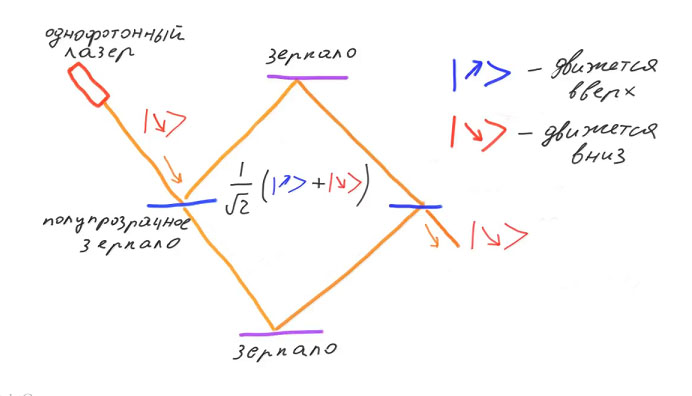
Les carrés de la valeur absolue des amplitudes de probabilité seront les probabilités classiques du passage et de la réflexion d'un photon. Après le premier miroir translucide, ils coïncideront avec les classiques: 50% que le photon monte et 50% qui descend. Après avoir traversé le deuxième miroir translucide, les amplitudes de probabilité changent leurs valeurs. De plus, dans le cadre de la mécanique quantique, on peut calculer que l'un d'eux sera nul, et l'autre. C'est-à-dire que le photon reviendra à l'état décrit par le vecteur de base vers le bas. Avec une probabilité de cent pour cent, après avoir traversé le deuxième miroir translucide, le photon descendra.
A la sortie du second miroir translucide, rien de plus qu'une interférence du photon avec lui-même n'est observée. Si nous essayons de savoir lequel des bras de l'interféromètre le photon a vraiment passé, alors l'interférence disparaît.
EXPÉRIENCEEssayons de placer des polariseurs circulaires dans l'interféromètre de Mach Zehnder. Sur un bras de l'interféromètre, installez un polariseur circulaire dans le sens horaire. Sur l'autre épaule, réglez le polariseur circulaire dans le sens antihoraire. De plus, sur le bras supérieur, un polariseur circulaire est installé directement après le miroir translucide. Sur le bras inférieur, un polariseur circulaire est installé après le miroir réfléchissant. Le fait est qu'un photon polarisé circulairement réfléchissant d'un miroir inverse la direction de la polarisation. Par conséquent, pour les photons qui ne sont pas réfléchis par un miroir translucide, la polarisation circulaire est établie après réflexion du miroir.
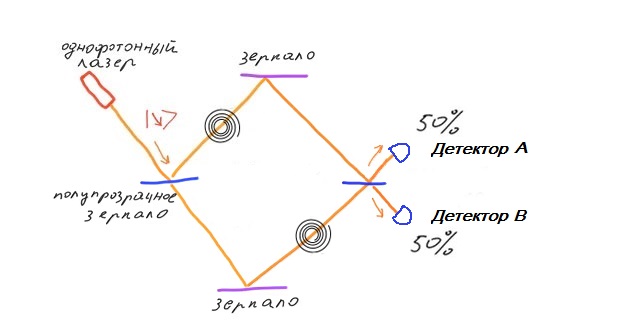
La présence de polariseurs dans l'interféromètre donne la possibilité de déterminer le chemin le long duquel le photon est passé. Par conséquent, le photon passera soit le long de l'épaule supérieure soit le long de l'épaule inférieure et ne traversera jamais les deux épaules en même temps. En conséquence, nous n'observons pas d'interférences à la sortie. L'absence d'interférence conduit au fait qu'en sortie nous obtenons 50% des photons dirigés vers le haut et 50% des photons dirigés vers le bas.
La situation changera si nous utilisons des particules quantiques enchevêtrées. Disons qu'un faisceau laser frappe un dispositif optique non linéaire: un cristal bêta-borate de baryum (BBO), grâce auquel un photon est converti en deux photons intriqués de fréquence inférieure. La paire de photons résultante suivra différents chemins, dont l'un traverse le polariseur et va directement au
détecteur 1 , et le second traverse un interféromètre à polariseurs circulaires et va au
détecteur 2 ou 3 .
Si nous plaçons un polariseur circulaire sur le chemin du premier photon, nous ne verrons pas non plus d'interférence. En conséquence, à la sortie, nous obtenons 50% des photons dirigés vers le haut et 50% des photons dirigés vers le bas.

Mais si un polariseur linéaire situé en diagonale est placé sur le chemin du premier photon, alors l'état intriqué fournira une polarisation diagonale supplémentaire à son partenaire. La présence d'une polarisation linéaire supplémentaire permettra aux photons de traverser les deux bras et d'interférer avec eux-mêmes. Dans ce cas, l'interférence aura une différence de phase (les photons dont les partenaires ont traversé le polariseur linéaire et dont les partenaires n'ont pas passé, créeront sur l'écran des interférences décalées les unes des autres). Malgré cela, le photon à la sortie du deuxième miroir translucide reviendra à l'état décrit par le vecteur de base vers le bas. Par conséquent, après avoir traversé le deuxième miroir translucide, tous les photons se déplaceront vers le bas.
Un tel schéma de mise en œuvre est pratique en ce qu'il ne nécessite pas d'établir un motif de coïncidence de particules enchevêtrées, d'émettre des photons un par un et d'analyser la position de chaque photon sur l'écran. En installant ou en supprimant un polariseur linéaire sur le chemin des particules enchevêtrées, vous pouvez instantanément affecter la répartition de leurs partenaires entre les détecteurs 2 et 3. Il suffit de comparer l'intensité du flux lumineux dans les deux détecteurs et de déterminer le bit d'information transmis. Naturellement, à la sortie du cristal BBO, tous les photons ne seront pas enchevêtrés. Le nombre de paires enchevêtrées représentera plusieurs dizaines de pour cent du total. Mais même un petit changement d'intensité lumineuse peut être détecté par des détecteurs, qui décrypteront les informations transmises. Le deuxième gros plus est que les paires enchevêtrées ne sont pas en état de superposition entre elles. Cela leur permet d'interagir avec l'environnement et de ne pas détruire les informations transmises, contrairement à la téléportation quantique, lorsque l'interaction avec l'air ou un câble optique détruit la fonction d'onde du photon.
PROBLÈMES CONNEXESL'utilisation de tels schémas permettra d'obtenir un délai minimum lors de la transmission d'informations sur de longues distances. La vitesse de transfert d'informations peut dépasser considérablement la vitesse de la lumière dans le vide. Certains soutiennent que STO / GTR interdit la transmission d'informations à une vitesse supérieure à la vitesse de la lumière. L'idée de la finitude de la vitesse de la lumière a été proposée par Poincaré et dérivée des formules de Maxwell. Dans ce cas, c'était initialement un champ électromagnétique, puis avec la main légère d'Albert Germanovich a été étendu à tous les objets matériels massifs et sans masse. Il est important de souligner qu'il n'a pas été question d'information, si vous ouvrez un livre sur STO / GRT, l'information n'est pas présente dans le formalisme mathématique. Par conséquent, lorsqu'ils prétendent que STO / GTR interdit la transmission d'informations au-dessus de la vitesse de la lumière, une hypothèse implicite est faite qu'il n'y a pas d'autre moyen que de "planter des informations" sur un faisceau de photons / électrons, etc. n'existe pas.
PRINCIPE DE CAUSEL'un des principaux problèmes du transfert instantané d'informations est la violation du principe de causalité. Mais vous pouvez voir que la physique moderne n'exige pas le respect de la causalité au niveau quantique, donc elle ne fait pas partie des postulats de la physique.
Il y a des expériences quantiques dans lesquelles la flèche du temps pourrait bien être inversée. Cependant, l'homme ne peut pas encore refuser de se conformer à la causalité, car cela contredit notre logique.
Selon la théorie de la relativité d'Einstein, le transfert instantané d'informations permet de recevoir des informations avant leur envoi. Par exemple, si nous décidons de nous envoyer des informations, nous pouvons mener une expérience de manière à obtenir des informations avant de les envoyer. Supposons que nous transmettons des informations à l'aide d'une paire complexe. Ensuite, un photon passera à travers l'interféromètre et arrivera au détecteur, et le deuxième photon, par exemple, ira vers la lune, où il sera réfléchi par le miroir et reviendra vers nous.
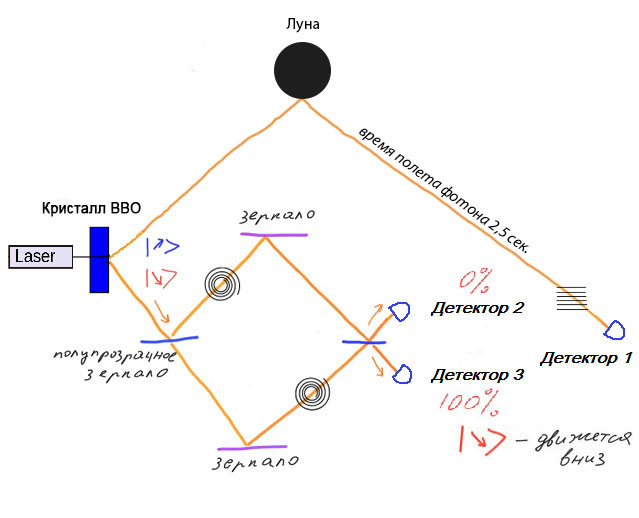
En installant ou en supprimant un polariseur linéaire sur le chemin du second photon, nous pouvons influencer le résultat à la sortie de l'interféromètre. Ainsi, en observant les détecteurs à la sortie de l'interféromètre, nous saurons à l'avance quelles informations nous décidons d'envoyer en 2,5 secondes (le temps de vol des photons vers la lune et retour). Cela peut conduire au «paradoxe du grand-père tué» lorsque nous avons vu un sens et décidé d'envoyer le contraire.
, . , . , . , .
– . , . , . , . . . , , .
, « ». , . .
, , . . , , (.. ). .
– . , . , , . , . , . .
, . . , « », ( ) . , . , . . (, , , , ) .
, . , , . , . , 70000 . , , -. ,
17 ,
10-20 .
PS , , - .
Sources:Quantum eraser experiment?