Construire des orbites de corps célestes en utilisant Python

Systèmes de référence pour déterminer l'orbite

Pour trouver les trajectoires des mouvements relatifs en mécanique classique, l'hypothèse du temps absolu dans tous les référentiels (inertiels et non inertiels) est utilisée.

En utilisant cette hypothèse, nous considérons le mouvement du même point dans deux référentiels différents $$$K$ et $$$K ^ {'}$ dont le second se déplace par rapport au premier à une vitesse arbitraire $$$\ vec {V (t)} = \ dot {\ vec {R (t)}}$ où $$$\ vec {R (t)}$ vecteur de rayon décrivant la position de l'origine du système de coordonnées $$$K ^ {'}$ par rapport au référentiel $$$K$ )

Nous décrirons le mouvement d'un point dans le système $$$K ^ {'}$ vecteur de rayon $$$\ vec {r ^ {'}} (t)$ dirigé depuis l'origine du système $$$K ^ {'}$ à la position actuelle du point. Puis le mouvement du point considéré par rapport au repère $$$K$ décrit par un vecteur de rayon $$$\ vec {r (t)}$ :

$$$\ vec {r} (t) = \ vec {r ^ {'}} (t) + \ vec {R} (t)$ , (1)

et vitesse relative $$$\ vec {v (t)}$

$$$\ vec {v} (t) = \ dot {\ vec {r ^ {'}}} (t) + \ dot {\ vec {R}} (t)$ , (2)

où $$$\ dot {\ vec {r ^ {'}}} (t)$ - vitesse du point par rapport au système $$$K ^ {'}$ ; $$$\ dot {\ vec {R}} (t)$ -vitesse de trame $$$K ^ {'}$ par rapport au référentiel $$$K$ .



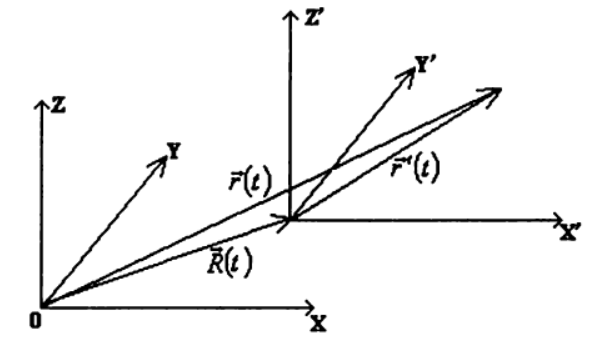
Ainsi, pour trouver la loi de mouvement d'un point dans un référentiel arbitraire $$$K$ nécessaire:

1) définir la loi du mouvement du point - $$$\ vec {r ^ {'}} (t)$ par rapport au référentiel $$$K ^ {'}$ ;
2) établir la loi du mouvement - $$$\ vec {R} (t)$ systèmes de référence $$$K ^ {'}$ par rapport au référentiel $$$K$
3) déterminer la loi de mouvement du point - $$$\ vec {r} (t) = \ vec {r ^ {'}} (t) + \ vec {R} (t)$ par rapport au référentiel $$$K$ .

Construction de l'orbite de la lune dans le référentiel héliocentrique

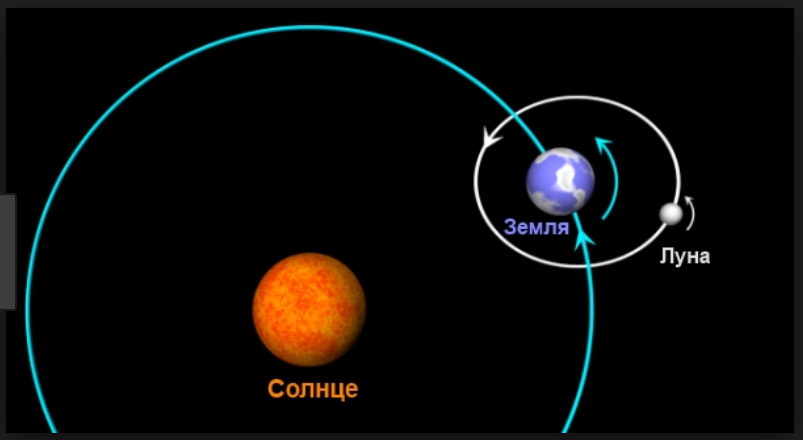
Dans le système de référence héliocentrique (système $$$K$ ) La Terre se déplace dans un cercle de rayon
$$$R_ {1} = 1,496 \ cdot 10 ^ {8}$ km (période de circulation $$$T_ {1} = 3 156 \ cdot 10 ^ {7}$ s.). La lune, à son tour, se déplace autour de la Terre (système K ') autour d'un cercle de rayon $$$R_ {2} = 3,844 \ cdot 10 ^ {5}$ km (période de circulation $$$T_ {2} = 2,36 \ cdot 10 ^ {6}$ s Comme on le sait [1,2], lorsqu'un point de matériau se déplace le long d'un cercle de rayon $$$R$ à vitesse angulaire constante $$$\ omega$ les coordonnées du vecteur rayon tirées de l'origine à la position courante du point changent selon la loi:

$$

$$\ vec {R (t)} = \ binom {R \ cdot cos (\ omega \ cdot t + \ varphi _ {0})} {R \ cdot sin (\ omega \ cdot t + \ varphi _ {0})} = \ binom {R \ cdot cos (\ frac {2 \ pi} {T}) + \ varphi _ {0})} {R \ cdot sin (\ frac {2 \ pi} {T} + \ varphi _ { 0})}, (3)$$

où $$$\ varphi _ {0}$ - la phase initiale caractérisant la position de la particule dans le temps $$$t = 0$ , que nous supposerons à l’avenir égal à zéro. Remplacement dans (3) $$$R$ sur $$$R_ {1}$ et $$$R_ {2}$ et en substituant en (1), on obtient la dépendance du vecteur rayon de la lune dans le repère héliocentrique dans le temps:

$$

$$\ vec {r (t)} = \ binom {x (t)} {y (t)} = \ binom {R_ {2} cos (\ frac {2 \ pi} {T_ {2}} t) + R_ {1} cos (\ frac {2 \ pi} {T_ {1}} t)} {R_ {2} sin (\ frac {2 \ pi} {T_ {2}} t) + R_ {1} sin (\ frac {2 \ pi} {T_ {1}} t)}, (4)$$

L'expression (4) définit l'orbite de la Lune ( $$$y = y (x (t))$ ) sous forme paramétrique, où le paramètre est le temps. Pour construire l'orbite souhaitée à l'aide de Python, nous avons défini les rayons des orbites et les périodes de rotation de la Terre et de la Lune.

La Terre se déplace dans un système de coordonnées héliocentrique ( $$$K$ ) son rayon d'orbite et la période de révolution sont respectivement égaux $$$R_ {1} = 1,496 \ cdot 10 ^ {8} km, T_ {1} = 3,156 \ cdot 10 ^ {7} s$ La lune se déplace autour de la terre dans un système de coordonnées ( $$$K ^ {'}$ ) son rayon d'orbite et la période de révolution sont respectivement égaux $$$R_ {2} = 3,844 \ cdot 10 ^ {5} km, T_ {2} = 2,36 \ cdot 10 ^ {6} s$ .

Au vu de (4), nous déterminons les fonctions de la dépendance des coordonnées dans le temps:

$$

$$\ binom {(X (t) = R_ {1} \ cdot cos (\ frac {2 \ pi} {T_ {1}} \ cdot t), Y (t) = R_ {1} \ cdot sin (\ frac {2 \ pi} {T_ {1}} \ cdot t)} {x (t) = R_ {2} \ cdot cos (\ frac {2 \ pi} {T_ {2}} \ cdot t), y (t) = R_ {2} \ cdot sin (\ frac {2 \ pi} {T_ {2}} \ cdot t)}, (5)$$

En utilisant (5), nous obtenons une paire de coordonnées pour l'orbite de la lune:

$$

$$\ binom {X_ {g} (t) = X (t) + x (t)} {Y_ {g} (t) = Y (t) + y (t)}, (6)$$

Nous fixons le nombre de points où les coordonnées N = 1000 et le temps discret sur l'intervalle de la période de rotation de la Terre sont calculés $$$dt = \ frac {T_ {1}} {N}$ . Nous allons écrire un programme et construire un graphique pour la zone de changement de coordonnées positives:


Nous obtenons:


Fig.1

Le programme créé vous permet d'élargir la tâche d'entraînement et de voir quelle sera l'orbite de la lune si le rayon de l'orbite de la lune est $$$R_ {2} = 3,844 \ cdot 10 ^ {7}$ . . Il est clair pour le lecteur qui n'a même pas de connaissances particulières en astronomie que la Lune ne peut pas avoir une telle orbite dans les champs non gravitationnels de la Terre, et un rayon hypothétique est utilisé pour étudier les conditions d'apparition de boucles . Nous apporterons les modifications appropriées au programme:


Nous obtenons:


Fig.2

En comparant les orbites de la lune illustrées à la Fig. 1 et 2, on retrouve leurs différences significatives. Pour expliquer les raisons de ces différences, il est nécessaire de comparer les vitesses linéaires de la lune dans les premier et deuxième cas et la vitesse linéaire de la terre.

Depuis la direction de la vitesse linéaire de la Terre par rapport au Soleil, ainsi que la direction de la vitesse linéaire de la Lune par rapport à la Terre, les changements dans le temps, et la vitesse reste constante en amplitude.

En tant que caractéristique quantitative du rapport des vitesses linéaires de la lune et de la terre dans le système de coordonnées héliocentriques, il convient de choisir la différence entre le module de vitesse linéaire de la terre et la projection de la vitesse linéaire de la lune sur la direction du vecteur de vitesse linéaire de la terre:

$$

$$v_ {o} (t) = \ left | \ vec {V} (t) \ right | - \ frac {(\ vec {V} (t) \ cdot \ vec {v} (t))} {\ left | \ vec {V} (t) \ right |}, (7)$$

Nous définissons les fonctions qui décrivent les lois de changement des composantes de la vitesse de la Terre et de la Lune:

$$

$$\ begin {matrix} V_ {x} (t) = \ frac {d} {dt} X (t), V_ {y} (t) = \ frac {d} {dt} Y (t) & \\ vx (t) = \ frac {d} {dt} x (t), vy (t) = \ frac {d} {dt} y (t) \ end {matrix}, (8)$$

Pour déterminer la vitesse résultante, en tenant compte de la projection, nous utilisons la relation:

$$$D (t) = \ sqrt {V_ {x} (t) ^ {2} + V_ {y} (t) ^ {2}} - \ sqrt {vx (t) ^ {2} + vy (t) ^ {2}} \ cdot \ frac {V_ {x} (t) \ cdot vx (t) + V_ {y} (t) \ cdot vy (t)} {\ sqrt {V_ {x} (t) ^ {2} + V_ {y} (t) ^ {2}} \ cdot \ sqrt {vx (t) ^ {2} + vy (t) ^ {2}}}, (9)$

Nous allons écrire un programme prenant en compte (5), (8), (9) et le rayon de l'orbite de la lune $$$R_ {2} = 3,844 \ cdot 10 ^ {5}$ km.:


Nous obtenons:


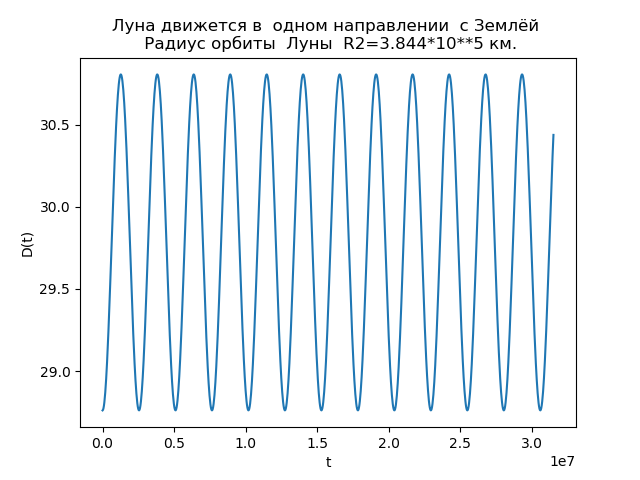Fig.3.

Nous écrirons un programme prenant en compte (5), (8), (9) et le rayon de l'orbite de la Lune R2 = 3.844 * 10 ** 7 km:


Nous obtenons:


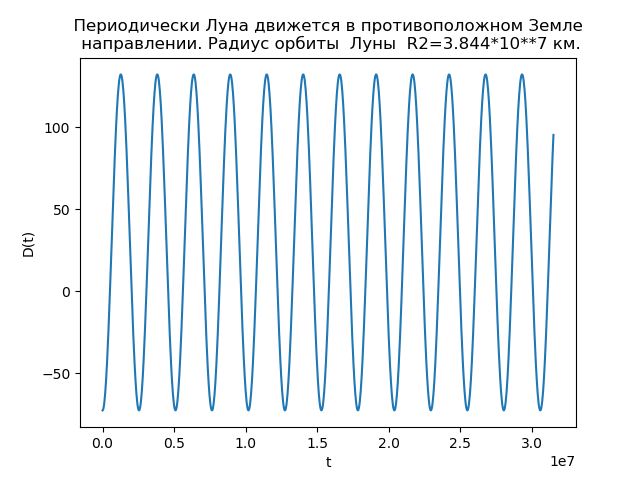Fig.4.

L'analyse des dépendances permet d'expliquer la raison des différences d'orbites. La fonction D (t) pour $$$R_ {2} = 3,844 \ cdot 10 ^ {5}$ km est toujours positif, c'est-à-dire que la lune se déplace toujours dans la direction du mouvement de la Terre et qu'aucune boucle ne se forme. À $$$R_ {2} = 3,844 \ cdot 10 ^ {7}$ valeur en km $$$D (t)$ prend des valeurs négatives, et il y a des moments où la lune se déplace dans la direction opposée à la direction du mouvement de la terre, et donc l'orbite a des boucles. C'était le sens d'utiliser l'orbite inexistante de la lune dans les calculs.

Construction de l'orbite de Mars dans le référentiel associé à la Terre

.


Dans le système de référence héliocentrique (système K), la Terre se déplace dans un cercle de rayon $$$R_ {1} = 1,496 \ cdot 10 ^ {8}$ km, période de circulation $$$T_ {1} = 365,24$ jour, Mars se déplace le long d'une ellipse dont le demi-grand axe $$$am = 2,28 \ cdot 10 ^ {8}$ km, la période de révolution de Mars $$$T_ {m} = 689,98$ jours., l'excentricité de l'orbite $$$e = 0,093$ [3]. Le mouvement de la Terre est décrit par le vecteur rayon R (t) défini par l'expression (3). Du fait que l'orbite de Mars est une ellipse, les dépendances $$$x = x (t), y = y (t)$ du temps sont paramétrées [4]:

$$$x (\ varepsilon) = a_ {m} \ cdot (cos (\ varepsilon) -e)$ , (10)

$$$y (\ varepsilon) = a_ {m} \ cdot \ sqrt {1-e ^ {2}} \ cdot sin (\ varepsilon)$ , (11)

$$$t (\ varepsilon) = \ frac {T_ {m}} {2 \ pi} \ cdot (\ varepsilon-e \ cdot sin (\ varepsilon))$ , (12)

Une révolution elliptique complète correspond à une modification du paramètre <img $$$\ varepsilon$ de 0 à $$$2 \ pi$ . Pour construire l'orbite de Mars, il est nécessaire de calculer les coordonnées des vecteurs de rayon aux mêmes moments qui décrivent la position de la Terre et de Mars dans le référentiel héliocentrique, puis en fonction de la relation $$$\ vec {r ^ {'}} (t) = \ vec {r} (t) - \ vec {R} (t)$ calculer les coordonnées de Mars dans le référentiel associé à la Terre.

Pour construire l'orbite de Mars dans le référentiel connecté à la Terre, nous utilisons les paramètres précédemment donnés des orbites de la Terre et de Mars, les relations (10) - (12), ainsi que les relations pour les coordonnées de la Terre:

$$$X (t) = R_ {1} \ cdot cos (\ frac {2 \ pi} {T_ {1}} t)$ , (13)

$$$Y (t) = R_ {1} \ cdot sin (\ frac {2 \ pi} {T_ {1}} t)$ , (14)

Il est à noter que le nombre de périodes de révolution de Mars autour du Soleil est $$$K = 9$ , alors le nombre de points auxquels le calcul doit être effectué et la distance entre eux seront déterminés à partir des relations:

$$$N = 4000 \ cdot K, \ varepsilon_ {i} = \ frac {2 \ pi} {N} \ cdot i, i = 0 ... N$ (15)


Nous obtenons:


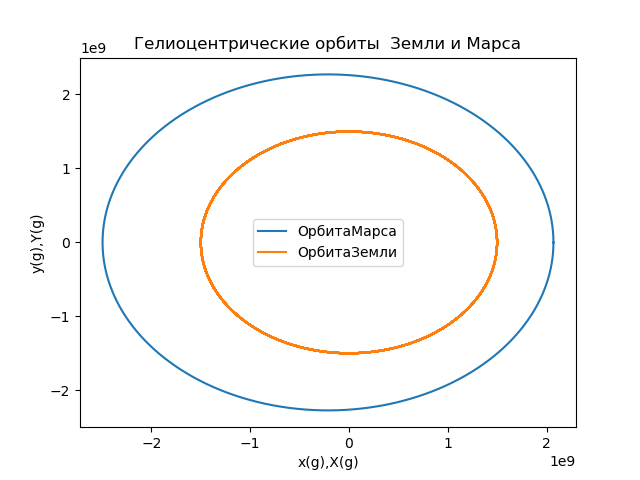Fig.5

Nous calculons les coordonnées du vecteur rayon décrivant la position de Mars dans le référentiel connecté à la Terre, et construisons les orbites (Fig.6) en utilisant la relation:

$$$x1_ {i} = x (\ varepsilon_ {i}) - X (t (\ varepsilon_ {i})), y1_ {i} = y (\ varepsilon_ {i}) - Y (t (\ varepsilon_ {i}) ))$ (16)


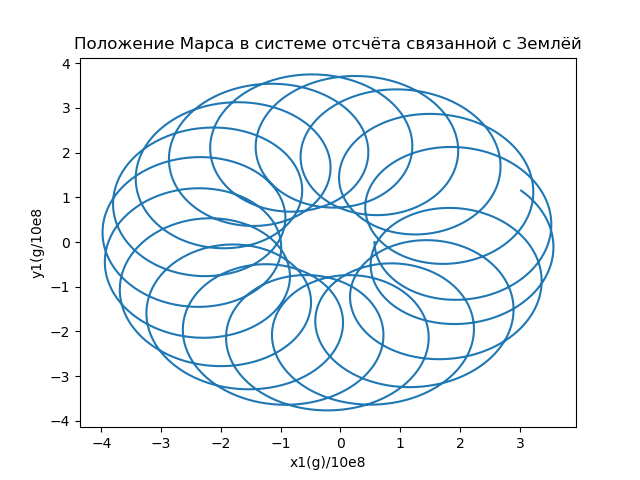Fig.6

Une autre caractéristique importante du mouvement de Mars (principalement pour les vols spatiaux interplanétaires) est la distance entre la Terre et Mars s (t), qui est déterminée par le module du vecteur de rayon décrivant la position de Mars dans le référentiel associé à la Terre. La dépendance de la distance entre la Terre et Mars au temps mesuré en années terrestres est présentée dans la Fig.7.


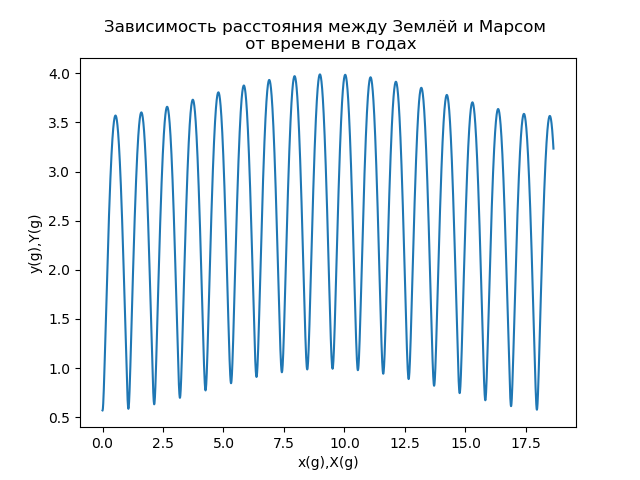Fig. 7

Une analyse de la dépendance représentée sur la figure 7 montre que la distance entre la Terre et Mars est une fonction périodique complexe du temps. Si nous utilisons la terminologie de la théorie du signal [5], alors nous pouvons dire à propos de la dépendance s (t) qu'il s'agit d'un signal modulé en amplitude, qui est généralement représenté comme le produit de deux fonctions d'une fonction haute fréquence (porteuse) et basse fréquence qui définit la modulation d'amplitude (enveloppe) :

$$$u (t) = (\ bar {u} + a \ cdot sin (\ omega_ {1} t)) \ cdot (1+ \ Delta a \ cdot sin (\ omega_ {2} t))$ (17)

où $$$\ bar {u}$ - composante constante de la fonction $$$u (t)$ ; $$$a$ - amplitude du signal; $$$\ omega_ {1}$ - fréquence porteuse; $$$\ Delta a$ - l'amplitude de la fonction qui fixe la profondeur de la modulation d'amplitude; $$$\ omega_ {2}$ - fréquence de la fonction de modulation.

La figure 7 montre que la période de la porteuse est d'environ 2 ans, la période de la fonction de modulation est d'environ 17 ans] 6].

Construction de l'orbite héliocentrique de la comète de Halley

La dernière fois que la comète de Halley a traversé son périhélie (le point d'orbite le plus proche du Soleil) le 9 février 1986. (Le Soleil lui-même est considéré comme situé à l'origine.)

Les coordonnées et les composantes de vitesse de la comète de Halley à ce moment étaient égales $$$p_ {0} = (0,325514, 0,459460, 0,166229)$ et $$$v_ {0} = (–9.096111, –6.916686, –1.305721)$ respectivement, et la distance ici est exprimée en unités astronomiques de longueur - a.u.d., ou simplement a.u. (unité astronomique, c'est-à-dire la longueur du grand semi-axe majeur de l'orbite terrestre), et le temps en années. Dans ces unités de mesure, les équations de mouvement tridimensionnelles de la comète ont la forme:

$$

$$\ left \ {\ begin {matrix} \ frac {d ^ {2} x} {dt ^ {2}} = - \ frac {\ mu \ cdot x} {r ^ {3}} \\ \ frac { d ^ {2} y} {dt ^ {2}} = - \ frac {\ mu \ cdot y} {r ^ {3}} \\ \ frac {d ^ {2} z} {dt ^ {2} } = - \ frac {\ mu \ cdot z} {r ^ {3}} \ end {matrix} \ right., (18)$$

(18)

où: $$$\ mu = 4 \ pi ^ {2}, r = \ sqrt {x ^ {2} + y ^ {2} + z ^ {2}}$


Nous obtenons:









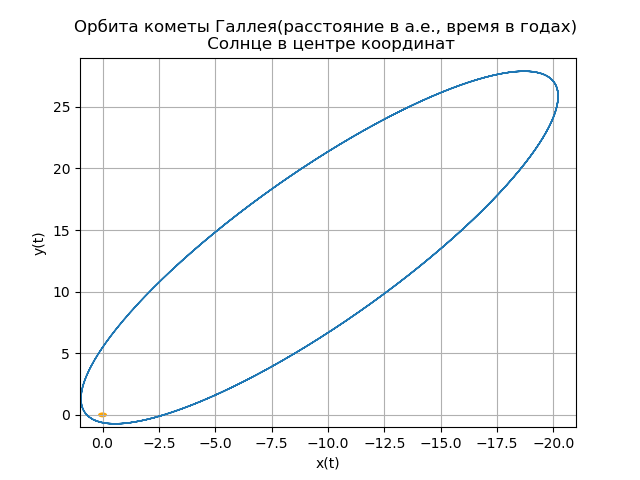
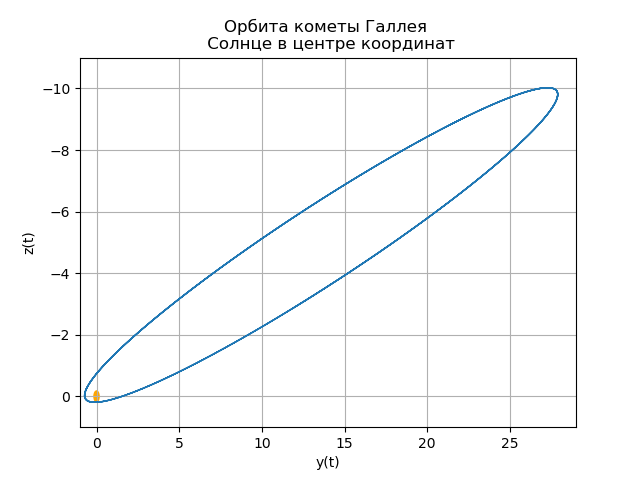
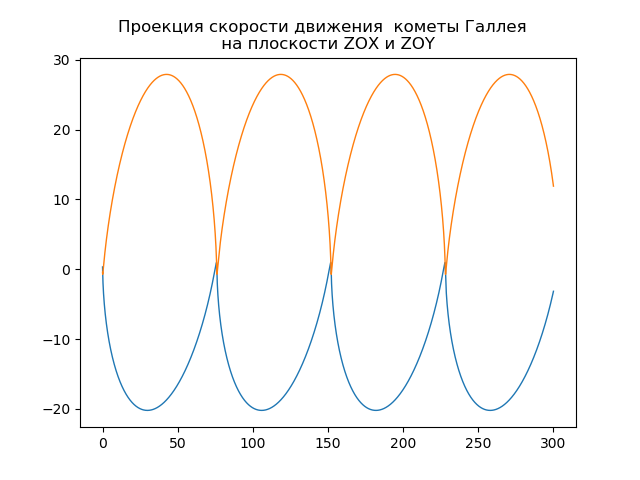Votre propre comète

Essayez une expérience. La nuit, vous montez votre télescope au sommet d'une colline non loin de chez vous. La nuit devrait être claire, sans nuages, étoilée et, si la fortune vous sourit: à 0h30, vous remarquerez une nouvelle comète.

Après des observations répétées les nuits suivantes, vous pourrez calculer ses coordonnées cette première nuit. Coordonnées dans le système de coordonnées héliocentrique: P0 = (x0, y0, z0) et le vecteur vitesse v0 = (vx0, vy0, vz0).

À l'aide de ces données, déterminez:

• la distance de la comète au Soleil au périhélie (le point d'orbite le plus proche du Soleil) et à l'aphélie (le point d'orbite le plus éloigné du Soleil);
• vitesse de la comète en passant par le périhélie et par l'aphélie;
• la période de révolution de la comète autour du Soleil;
• les deux prochaines dates, la comète passe à travers le périhélie.

Si nous mesurons la distance en unités astronomiques et le temps en années, alors l'équation du mouvement de la comète prendra la forme (18). Pour votre propre comète, sélectionnez des coordonnées de départ et des vitesses arbitraires du même ordre que la comète de Halley.

Si nécessaire, refaites un choix arbitraire de la position initiale et du vecteur vitesse jusqu'à ce que vous obteniez une orbite excentrique plausible qui dépasse l'orbite terrestre (comme la plupart des vraies comètes).

Références:

1. Feynman R., Leighton R., Sands M. Feynman Lectures in Physics. 3e éd. T. 1.-2. M .: Mir, 1977.
2. Matveev A.N.Mécanique et théorie de la relativité. M.: Plus haut. école., 1986.
3. Encyclopédie physique. T. 3. M .: Big Russian Encyclopedia, 1992.
4. Landau L.D., Lifshits E.M.Cours de physique théorique. La mécanique. M .: Fu-matgiz, 1958.
5. Baskakov S.I.Circuits et signaux d'ingénierie radio. M.: Plus haut. école., 1988.
6. Porshnev C.V. Simulation informatique des processus physiques à l'aide du package mathcad .