Travailler avec des matrices numériques en général et résoudre des systèmes d'équations algébriques linéaires en particulier est un problème mathématique et algorithmique classique qui est largement utilisé dans la modélisation et le calcul d'une énorme classe de processus métier (par exemple, lors du calcul des coûts). Lors de la création et de l'exploitation des configurations 1C: Enterprise, de nombreux développeurs ont été confrontés à la nécessité d'implémenter manuellement des algorithmes de calcul SLAU, puis au problème d'une longue attente d'une solution.
«1C: Enterprise» 8.3.14 contiendra des fonctionnalités qui peuvent réduire considérablement le temps nécessaire pour résoudre des systèmes d'équations linéaires en utilisant un algorithme basé sur la théorie des graphes.
Il est optimisé pour une utilisation sur des données ayant une structure clairsemée (c'est-à-dire ne contenant pas plus de 10% de coefficients non nuls dans les équations) et, en moyenne et dans le meilleur des cas, démontre les asymptotiques (n⋅log (n) ⋅log (n)), où n est le nombre de variables, et dans le pire des cas (lorsque le système est plein ~ 100%), son comportement asymptotique est comparable aux algorithmes classiques (Θ (n
3 )). De plus, sur les systèmes avec ~ 10
5 inconnues, l'algorithme montre une accélération des centaines de fois en comparaison avec ceux implémentés dans les bibliothèques d'algèbre linéaire spécialisées (par exemple,
superlu ou
lapack ).
Important: l'article et l'algorithme décrit nécessitent une compréhension de l'algèbre linéaire et de la théorie des graphes au niveau de la première année d'une université.Présentation du SLAE sous forme de graphique
Considérons le système le plus simple et clairsemé d'équations linéaires:
Attention: le système est généré aléatoirement et sera utilisé ultérieurement pour illustrer les étapes de l'algorithmeÀ première vue, une association avec un autre objet mathématique apparaît - la matrice d'adjacence du graphe. Alors pourquoi ne pas convertir les données en listes d'adjacence, économiser de la RAM lors de l'exécution et accélérer l'accès à des coefficients non nuls?
Pour ce faire, il suffit de transposer la matrice et d'établir l'invariant
"A [i] [j] = z ⇔ la i-ème variable entre dans la j-ème équation avec le coefficient z" , puis pour tout A non différent de A [i] [j] construire l'arête correspondante du sommet i au sommet j.
Le graphique résultant ressemblera à ceci:
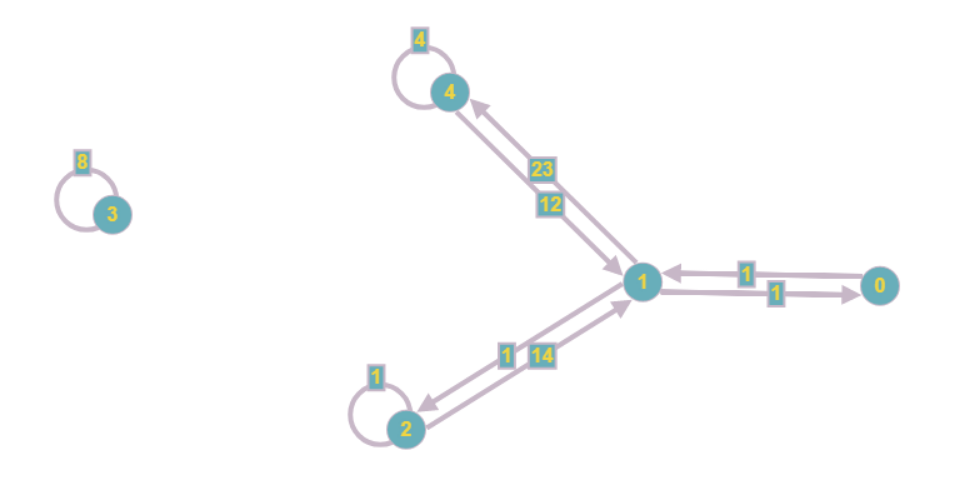
Même visuellement, il s'avère moins lourd et les coûts de mémoire asymptotique diminuent de O (n
2 ) à O (n + m), où m est le nombre de coefficients dans le système.
Isolement des composants faiblement connectés
La deuxième idée algorithmique qui vient à l'esprit lorsque l'on considère l'entité résultante: l'utilisation du principe de «diviser pour régner». En termes de graphique, cela conduit à la séparation de l'ensemble des sommets en composants faiblement connectés.
Permettez-moi de vous rappeler que la composante faiblement connectée est un tel sous-ensemble de sommets qui est maximal en inclusion, entre deux, il existe un chemin à partir des bords dans un graphe non orienté. Nous pouvons obtenir un graphique non orienté à partir de celui d'origine, par exemple, en ajoutant l'opposé à chaque bord (avec suppression ultérieure). Ensuite, un sommet de la connexion inclura tous les sommets que nous pouvons atteindre lorsque nous parcourons le graphique en profondeur.
Après séparation des composants faiblement connectés, le graphique prendra la forme suivante:
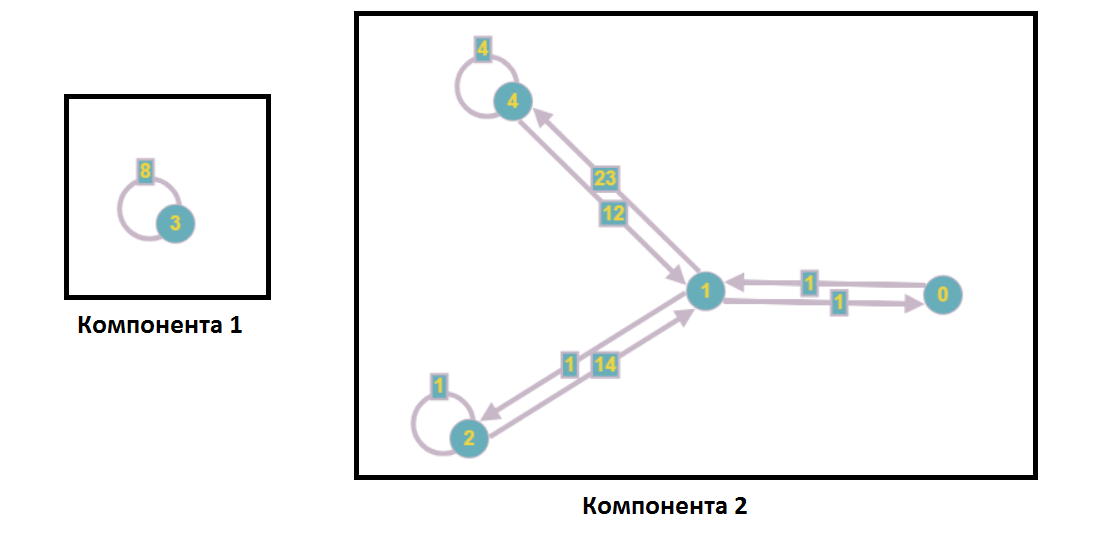
Dans le cadre de l'analyse d'un système d'équations linéaires, cela signifie qu'aucun sommet du premier composant n'est inclus dans les équations avec les nombres du deuxième composant et vice versa, c'est-à-dire que nous pouvons résoudre ces sous-systèmes indépendamment (par exemple, en parallèle).
Réduction du sommet du graphe
L'étape suivante de l'algorithme est exactement ce qu'est l'optimisation pour travailler avec des matrices clairsemées. Même dans le graphique de l'exemple, il y a des pics «suspendus», ce qui signifie que certaines des équations ne comprennent qu'une seule inconnue et, comme nous le savons, la valeur de cette inconnue est facile à trouver.
Pour déterminer de telles équations, il est proposé de stocker un tableau de listes contenant le nombre de variables incluses dans l'équation portant le numéro de cet élément de tableau. Ensuite, lorsque la liste atteint la taille unitaire, nous pouvons réduire le très «seul» sommet et informer le reste des équations des autres équations dans lesquelles ce sommet entre.
Ainsi, nous pouvons réduire le sommet 3 de l'exemple immédiatement après avoir entièrement traité le composant:
Nous procédons de la même manière avec l'équation 0, car elle ne contient qu'une seule variable:
D'autres équations changeront également après avoir trouvé ce résultat:
$$ afficher $$ 1⋅_1 + 1⋅_2 = 3⇒1⋅_2 = 3-1 = 2 $$ afficher $$
Le graphique prend la forme suivante:
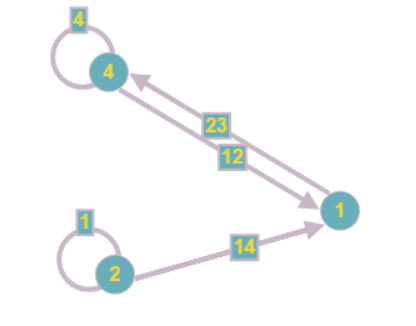
Notez que lors de la réduction d'un sommet, d'autres peuvent également apparaître qui contiennent également un inconnu. Cette étape de l'algorithme doit donc être répétée jusqu'à ce qu'au moins l'un des sommets puisse être réduit.
Reconstruction du graphique
Les lecteurs les plus attentifs pourraient remarquer qu'une situation est possible dans laquelle chacun des sommets du graphique aura un degré d'occurrence d'au moins deux et il sera impossible de continuer à réduire systématiquement les sommets.
L'exemple le plus simple d'un tel graphique: chaque sommet a un degré d'occurrence égal à deux, aucun des sommets ne peut être réduit.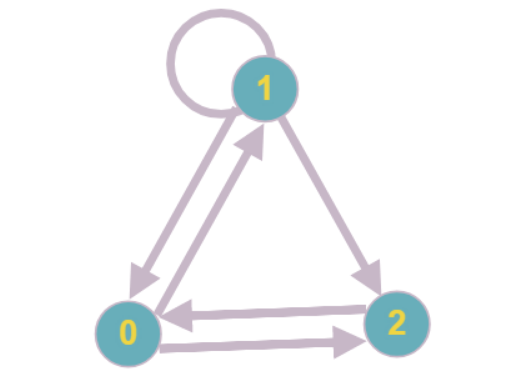
Dans le cadre de l'optimisation des matrices clairsemées, il est supposé que ces sous-graphiques seront de petite taille, cependant, vous devez toujours travailler avec eux. Pour calculer les valeurs des inconnues qui font partie du sous-système d'équations, il est proposé d'utiliser des méthodes classiques pour résoudre les SLAE (c'est pourquoi l'introduction indique que pour une matrice dans laquelle tous ou presque tous les coefficients des équations sont non nuls, notre algorithme aura la même complexité asymptotique que les standards) )
Par exemple, vous pouvez ramener l'ensemble des sommets restants après réduction dans la forme matricielle et lui appliquer
la méthode de Gauss pour résoudre les SLAE . Ainsi, nous obtiendrons la solution exacte, et la vitesse de l'algorithme sera réduite en raison du traitement non pas du système entier, mais seulement d'une partie de celui-ci.
Test d'algorithme
Pour tester l'implémentation logicielle de l'algorithme, nous avons pris plusieurs systèmes réels d'équations de grand volume, ainsi qu'un grand nombre de systèmes générés aléatoirement.
La génération d'un système d'équations aléatoire est passée par l'addition séquentielle de bords de poids arbitraire entre deux sommets aléatoires. Au total, le système était plein à 5-10%. L'exactitude des solutions a été vérifiée en substituant les réponses obtenues au système d'équations d'origine.
Les systèmes allaient de 1 000 à 200 000 inconnusPour comparer les performances, nous avons utilisé les bibliothèques les plus populaires pour résoudre les problèmes d'algèbre linéaire, telles que superlu et lapack. Bien sûr, ces bibliothèques sont axées sur la résolution d'une large classe de problèmes et la solution de SLAE en eux n'est en aucune façon optimisée, de sorte que la différence de vitesse s'est avérée importante.
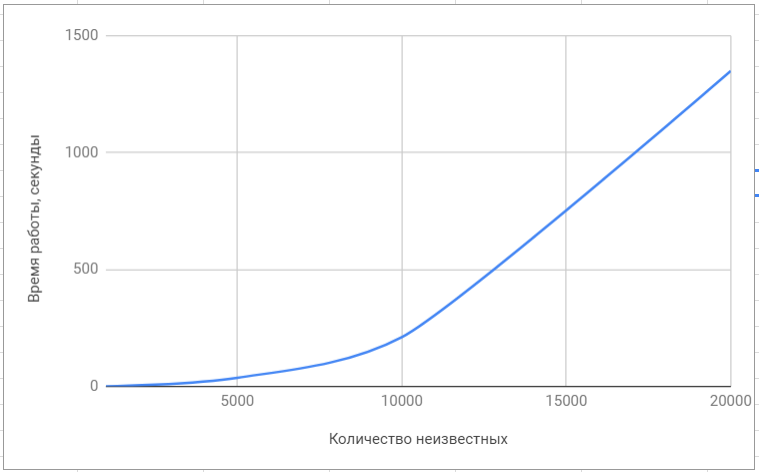Test de la bibliothèque lapack
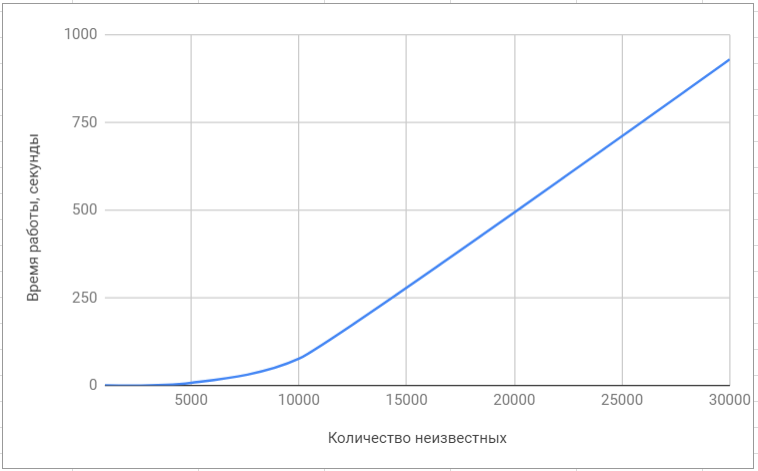Test de la bibliothèque 'superlu'Voici la comparaison finale de notre algorithme avec les algorithmes implémentés dans les bibliothèques populaires:
Conclusion
Même si vous n'êtes pas un développeur de configuration 1C: Enterprise, les idées et les méthodes d'optimisation décrites dans cet article peuvent être utilisées par vous non seulement lors de la mise en œuvre d'un algorithme pour résoudre les SLAE, mais également pour toute une classe de problèmes d'algèbre linéaire associés aux matrices.
Pour les développeurs 1C, nous ajoutons que la nouvelle fonctionnalité de la solution SLAE prend en charge l'utilisation parallèle des ressources informatiques, et vous pouvez ajuster le nombre de threads de calcul utilisés.