Richard Hamming: Chapitre 20. Modélisation - III

«Le but de ce cours est de vous préparer à votre avenir technique.»

Il reste à publier 2 chapitres ...

Modélisation - III

Je continuerai la direction générale donnée dans le chapitre précédent, mais cette fois je me concentrerai sur l'ancienne expression «Garbage in - garbage out», qui est souvent abrégée en GIGO (garbage in, garbage out). L'idée est que si vous mettez des données collectées de manière inexacte et des expressions mal définies sur l'entrée, la sortie ne peut obtenir que des résultats incorrects. Le contraire est également implicitement supposé: à partir de la disponibilité de données d'entrée précises, le résultat correct est obtenu. Je montrerai que ces deux hypothèses peuvent être fausses.

Souvent, la modélisation est basée sur la résolution d'équations différentielles, donc pour commencer, nous considérerons l'équation différentielle la plus simple du premier ordre de la forme



Comme vous vous en souvenez, le champ de direction correspond aux lignes construites à chaque point du plan xy, avec les coefficients angulaires donnés par l'équation différentielle (figure 20.I). Par exemple, une équation différentielle a un champ de direction illustré à la figure 20.II.





Figure 20.I

Pour chaque cercle concentrique,



de telle sorte que la pente de la ligne est toujours la même et dépend de la valeur de k. Ces courbes sont appelées isoclines .

Voyons maintenant le champ de direction d'une autre équation différentielle (figure 20.III). Sur le côté gauche, nous voyons un champ de directions divergentes, ce qui signifie que de petits changements dans les valeurs initiales ou de petites erreurs de calcul entraîneront une grande différence dans les valeurs au milieu du chemin. Sur le côté droit, nous voyons que le champ de direction converge. Cela signifie qu'avec une plus grande différence au milieu du chemin, la différence de valeurs à l'extrémité droite sera petite. Cet exemple simple montre comment les petites erreurs peuvent devenir grandes, les grandes erreurs petites et, en outre, comment les petites erreurs peuvent devenir grandes, puis à nouveau petites. Par conséquent, la précision de la solution dépend de l'intervalle spécifique auquel la solution est calculée. Il n'y a pas de précision générale absolue.



Figure 20.II



Figure 20.III

Ces considérations sont conçues pour la fonction


qui est une solution à l'équation différentielle



Vous avez probablement imaginé un «tuyau» qui se dilate d'abord puis se rétrécit autour de la «vraie solution exacte» de l'équation. Une telle représentation est parfaite pour le cas de deux mesures, mais quand j'ai un système de n telles équations différentielles - 28 dans le cas du problème des missiles intercepteurs pour la Marine mentionné plus haut - alors ces «tuyaux» autour de la vraie solution de l'équation ne sont pas ce qu'ils semblent à première vue. Une figure composée de quatre cercles en deux dimensions conduit au paradoxe des n-dimensions pour l'espace à dix dimensions décrit au chapitre 9. Ceci est juste une autre vue du problème de la modélisation stable et instable, décrit dans le chapitre précédent. Cette fois, je vais donner des exemples spécifiques liés aux équations différentielles.

Comment résoudre numériquement les équations différentielles? En partant de l'équation différentielle de premier ordre habituelle, nous dessinons un champ de directions. Notre tâche consiste à avoir une valeur initiale donnée calculer la valeur au prochain point d'intérêt le plus proche de nous. Si nous prenons le coefficient de pente local de la droite donnée par l'équation différentielle et faisons un petit pas en avant le long de la tangente, alors nous n'introduirons qu'une petite erreur (figure 20.IV).

En utilisant ce nouveau point, nous passerons au point suivant, mais comme on peut le voir sur la figure, nous nous écartons progressivement de la vraie courbe, car nous utilisons le coefficient de pente de l'étape précédente, et non le vrai coefficient de pente pour l'intervalle actuel. Pour éviter cet effet, nous «prédisons» une certaine valeur, puis nous l'utilisons pour estimer le coefficient angulaire à ce point (en utilisant l'équation différentielle), puis nous utilisons la valeur moyenne du coefficient angulaire aux deux limites de l'intervalle comme coefficient angulaire pour cet intervalle.

Ensuite, en utilisant cette pente moyenne, nous allons un peu plus loin, cette fois en utilisant la formule de «correction». Si les valeurs obtenues à l'aide des formules de «prévision» et de «correction» sont suffisamment proches, nous supposons que nos calculs sont suffisamment précis, sinon nous devons réduire la taille du pas. Si la différence entre les valeurs est trop petite, alors nous devons augmenter la taille du pas. Ainsi, le schéma prédicteur-correcteur traditionnel a un mécanisme intégré pour vérifier les erreurs à chaque étape, mais cette erreur à une étape particulière n'est en aucun cas et en aucun cas une erreur accumulée commune! Il est absolument clair que l'erreur accumulée dépend de la convergence ou de la divergence du champ de direction.



Figure 20.IV



Figure 20.V

Nous avons utilisé des lignes droites simples pour l'étape de prévision et l'étape de correction. L'utilisation de polynômes de degrés supérieurs donne un résultat plus précis; des polynômes d'un quart de degré sont généralement utilisés (la solution d'équations différentielles par la méthode Adams-Bashfort, la méthode Milne, la méthode Hamming, etc.). Ainsi, nous devons utiliser les valeurs de la fonction et ses dérivées à plusieurs points précédents pour prédire la valeur de la fonction au point suivant, après quoi nous utilisons la substitution de cette valeur dans l'équation différentielle et approximons la nouvelle valeur du coefficient angulaire. En utilisant les valeurs nouvelles et précédentes du coefficient angulaire ainsi que les valeurs de la fonction souhaitée, nous corrigeons la valeur obtenue. Il est temps de remarquer que le correcteur n'est rien de plus qu'un filtre récursif numérique dans lequel les valeurs d'entrée sont des dérivées et les valeurs de sortie sont les valeurs de la fonction souhaitée.

La stabilité et les autres concepts discutés précédemment restent pertinents. Comme mentionné précédemment, il existe une boucle de rétroaction supplémentaire pour la solution prédite de l'équation différentielle, qui à son tour est utilisée dans le calcul du coefficient angulaire ajusté. Ces deux valeurs sont utilisées pour résoudre l'équation différentielle, les filtres numériques récursifs ne sont que des formules, et rien de plus. Cependant, ce ne sont pas des caractéristiques de transfert, car elles sont couramment considérées dans la théorie des filtres numériques. Dans ce cas, le calcul des valeurs de l'équation différentielle a simplement lieu. Dans ce cas, la différence entre les approches est significative: dans les filtres numériques, le signal est traité linéairement, tandis que dans la résolution d'équations différentielles, il y a la non-linéarité, qui est introduite en calculant les valeurs des dérivées de la fonction. Ce n'est pas la même chose qu'un filtre numérique.

Si vous résolvez un système de n équations différentielles, alors vous avez affaire à un vecteur de n composantes. Vous prédisez la valeur suivante de chaque composant, évaluez chacune des n dérivées, ajustez chacune des valeurs prédites, puis acceptez le résultat du calcul à cette étape ou le rejetez si l'erreur locale est trop importante. Vous avez tendance à considérer les petites erreurs comme un «tuyau» entourant un vrai chemin calculé. Et encore une fois, je vous exhorte à vous souvenir du paradoxe des quatre cercles dans les espaces de grande dimension. De tels «tuyaux» ne sont peut-être pas ce qu'ils semblent à première vue.

Permettez-moi maintenant de souligner la différence significative entre les deux approches: les méthodes de calcul et la théorie des filtres numériques. Dans les manuels courants, seules les méthodes de mathématiques computationnelles sont décrites qui rapprochent les fonctions par des polynômes. Les filtres récursifs utilisent des fréquences dans les formules d'évaluation! Cela conduit à des différences importantes!

Pour voir la différence, imaginons que nous développons un simulateur d'un atterrissage humain sur Mars. L'approche classique se concentre sur la forme de la trajectoire d'atterrissage et utilise l'approximation polynomiale pour les régions locales. Le chemin résultant aura des points de rupture en accélération, tandis que nous progressons pas à pas d'un intervalle à l'autre. Dans le cas de l'approche par fréquence, nous nous concentrerons sur l'obtention des bonnes fréquences et laisserons l'emplacement être ce qu'il s'avère être. Dans le cas idéal, les deux trajectoires seront les mêmes, mais en pratique, elles peuvent différer considérablement.

Quelle randonnée dois-je utiliser? Plus vous y réfléchissez, plus vous serez enclin à croire que le pilote du simulateur veut avoir une «idée» du comportement du module d'atterrissage, et il semble que la réponse en fréquence du simulateur devrait être bien «ressentie» par le pilote. Si l'emplacement est légèrement différent, la boucle de rétroaction compensera cette déviation pendant le processus d'atterrissage, mais si la «sensation» de la commande diffère pendant le vol réel, le pilote sera préoccupé par de nouvelles «sensations» qui n'étaient pas dans le simulateur. Il m'a toujours semblé que les simulateurs devraient autant que possible préparer les pilotes à de vraies sensations (bien sûr, nous ne pouvons pas simuler une faible gravité sur Mars pendant longtemps), afin qu'ils se sentent à l'aise lorsqu'ils rencontrent en réalité une situation avec laquelle ils rencontré à plusieurs reprises dans le simulateur. Hélas, nous savons trop peu sur ce que le pilote «ressent». Le pilote ne détecte-t-il que les fréquences réelles de l'expansion de Fourier, ou détecte-t-il également les fréquences complexes de Laplace qui s'estompent (ou peut-être devrions-nous utiliser des ondelettes?). Est-ce que différents pilotes ressentent les mêmes choses? Nous devons en savoir plus que nous ne le savons maintenant sur ces conditions de conception essentielles.

La situation décrite ci-dessus est une contradiction standard entre l'approche mathématique et l'ingénierie pour résoudre le problème. Ces approches ont des objectifs différents dans la résolution d'équations différentielles (comme dans le cas de nombreux autres problèmes), elles conduisent donc à des résultats différents. Si vous venez avec la modélisation, vous verrez qu'il y a des nuances cachées qui s'avèrent être très importantes dans la pratique, mais dont les mathématiciens ne savent rien et nieront de toutes les manières les conséquences de les négliger. Jetons un coup d'œil à deux chemins (figure 20.IV), que j'ai approximativement estimés. La courbe supérieure décrit plus précisément l'emplacement, mais les virages donnent une «sensation» complètement différente par rapport au monde réel, la deuxième courbe est plus erronée dans l'emplacement, mais a une plus grande précision en termes de «sensation». J'ai de nouveau clairement démontré pourquoi je crois qu'une personne ayant une compréhension approfondie du sujet du problème devrait également comprendre les méthodes mathématiques pour le résoudre, et ne pas s'appuyer sur les méthodes traditionnelles de solution.

Maintenant, je veux raconter une autre histoire sur les premiers jours du test du système de défense antimissile Nike. À cette époque, des essais sur le terrain avaient lieu à White Sands, qui était également appelé «test de téléphone sur le terrain». Il s'agissait de lancements d'essai dans lesquels la fusée devait suivre une trajectoire prédéterminée et exploser au dernier moment, de sorte que toute l'énergie de l'explosion ne dépassait pas les limites d'un certain territoire et causait plus de dégâts, ce qui était préférable à une goutte plus douce de parties individuelles de la fusée sur le sol, ce qui devrait avoir fait moins de dégâts. L'objectif des tests était d'obtenir des mesures réelles de portance et de traînée en fonction de l'altitude et de la vitesse de vol afin de déboguer et d'améliorer la conception.

Quand j'ai rencontré mon ami qui était revenu des tests, il a erré dans les couloirs des laboratoires Bell et avait l'air plutôt misérable. Pourquoi? Parce que les deux premiers des six lancements programmés ont échoué au milieu du vol et personne ne savait pourquoi. Les données nécessaires pour les étapes de conception ultérieures n'étaient pas disponibles, ce qui a entraîné de graves problèmes pour l'ensemble du projet. J'ai dit que s'il pouvait me fournir des équations différentielles décrivant le vol, je pourrais demander à la fille de les résoudre (avoir accès à de gros ordinateurs à la fin des années 40 n'était pas facile). Après environ une semaine, ils ont fourni sept équations différentielles de premier ordre et la fille était prête à commencer. Mais quelles étaient les conditions initiales un moment avant le début des problèmes en vol? (À cette époque, nous n'avions pas assez de puissance de calcul pour calculer rapidement toute la trajectoire de vol.) Ils ne savaient pas! Les données de télémétrie étaient incompréhensibles un moment avant l'échec. Je n'ai pas été surpris et cela ne m'a pas dérangé. Nous avons donc utilisé les valeurs estimées de l'altitude, de la vitesse de vol, de l'angle d'attaque, etc. - une condition initiale pour chacune des variables décrivant la trajectoire de vol. En d'autres termes, j'avais des ordures à l'entrée. Mais plus tôt, j'ai réalisé que la nature des tests sur le terrain que nous avons simulés était telle que les petits écarts par rapport à la trajectoire proposée étaient automatiquement corrigés par le système de guidage! Je faisais face à un champ de directions très convergent.

Nous avons constaté que la fusée était stable le long des axes transversal et vertical, mais lorsque l'un d'eux s'est stabilisé, un excès d'énergie a entraîné des oscillations le long de l'autre axe. Ainsi, il y avait non seulement des oscillations le long des axes transversaux et verticaux, mais aussi une transmission périodique d'énergie croissante entre eux, provoquée par la rotation de la fusée autour de son axe longitudinal. Dès que les courbes calculées pour une petite partie de la trajectoire ont été démontrées, tout le monde s'est immédiatement rendu compte que la stabilisation croisée n'était pas prise en compte, et tout le monde a su la corriger. Nous avons donc obtenu une solution qui nous a également permis de lire les données de télémétrie corrompues obtenues lors des tests et de clarifier la période de transfert d'énergie - en fait, fournir les équations différentielles correctes pour les calculs. J'ai eu un peu de travail, sauf pour m'assurer que la fille avec la calculatrice de bureau a tout calculé honnêtement. Donc, en mai, le mérite était de comprendre que (1) nous pouvons simuler ce qui s'est passé (maintenant c'est une routine pour enquêter sur les accidents, mais c'était une innovation) et (2) le champ de direction converge, donc les conditions initiales peuvent ne pas être spécifiées exactement.

Je vous ai raconté cette histoire afin de montrer que le principe GIGO ne fonctionne pas toujours. Une histoire similaire m'est arrivée lors d'une première simulation de bombe à Los Alamos. Peu à peu, j'ai compris que nos calculs, construits pour l'équation d'état, étaient basés sur des données plutôt inexactes. L'équation d'état concerne la pression et la densité d'une substance (également la température, mais je vais l'omettre dans cet exemple). Les données des laboratoires à haute pression, les approximations obtenues à partir de l'étude des tremblements de terre, de la densité du noyau stellaire et de la théorie asymptotique des pressions infinies ont été représentées sous forme de points sur un très grand papier millimétré (figure 20.VII). Ensuite, en utilisant des motifs, nous avons dessiné des courbes reliant les points diffusés. Ensuite, sur la base de ces courbes, nous avons construit des tableaux de valeurs de fonction avec une précision de 3 décimales. Cela signifie que nous avons simplement supposé 0 ou 5 à la 4e décimale. Nous avons utilisé ces données pour créer des tableaux jusqu'aux 5e et 6e décimales. Sur la base de ces tableaux, nos autres calculs ont été construits. À cette époque, comme je l'ai déjà mentionné, j'étais une sorte de calculatrice, et mon travail consistait à compter et donc à libérer les physiciens de cette profession, pour leur permettre de faire leur travail.



Figure 20.VII

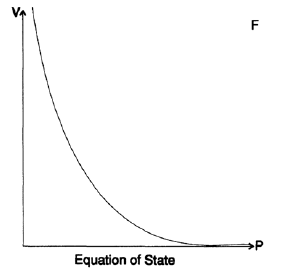
Après la fin de la guerre, je suis resté à Los Alamos pendant encore six mois, et l'une des raisons pour lesquelles j'ai fait cela était parce que je voulais comprendre comment de telles données inexactes pouvaient conduire à une simulation aussi précise de la conception finale. J'y ai réfléchi longtemps et j'ai trouvé la réponse. Au milieu des calculs, nous avons utilisé des différences finies de second ordre. La différence de premier ordre a montré la valeur de la force d'un côté de chaque coquille, et les différences des coquilles adjacentes des deux côtés ont donné la force résultante, qui déplace la coquille. Nous avons été obligés d'utiliser des coques minces, nous avons donc soustrait des nombres très proches les uns des autres, et nous devions utiliser de nombreux chiffres après la virgule décimale. D'autres études ont montré que lorsque la «chose» a explosé, la coquille s'est déplacée vers le haut le long de la courbe, et probablement parfois partiellement reculée, de sorte que toute erreur locale dans l'équation d'état était proche de la valeur moyenne. Il était vraiment important d'obtenir la courbure de l'équation d'état et, comme déjà indiqué, elle aurait dû être précise en moyenne. Ainsi, des ordures en entrée, mais des résultats de sortie plus précis que jamais!

Ces trois exemples montrent ce qui a été implicitement mentionné précédemment - s'il existe une boucle de rétroaction pour les variables utilisées dans le problème, il n'est pas nécessaire de connaître exactement leurs valeurs. Sur cette base, la remarquable idée de G.S. Black sur la façon de construire une boucle de rétroaction dans les amplificateurs (figure 20.VIII): tant que le gain est très élevé, seule la résistance d'une résistance doit être adaptée avec précision, toutes les autres parties peuvent être mis en œuvre avec une faible précision. Pour le circuit illustré à la figure 20.VIII, nous obtenons les expressions suivantes:



Figure 20.VIII

Comme vous pouvez le voir, presque toute l'incertitude de mesure est concentrée dans une résistance avec une valeur nominale de 1/10, tandis que le coefficient de transmission peut être inexact. La boucle de rétroaction de Black nous permet donc de créer des éléments précis à partir de pièces inexactes.



Maintenant, vous voyez pourquoi je ne peux pas vous donner une formule élégante adaptée à toutes les occasions. Cela devrait dépendre des calculs effectués sur des quantités spécifiques. Les valeurs inexactes passeront-elles par une boucle de rétroaction qui compense l'erreur, ou les erreurs sortiront-elles du système sans protection de rétroaction? Si aucune rétroaction n'est fournie pour les variables, il est essentiel d'obtenir leurs valeurs exactes.
Ainsi, la prise de conscience de ce fait peut affecter la conception du système! Un système bien conçu vous évite d'avoir à utiliser un grand nombre de composants de précision. Mais de tels principes de conception sont encore mal compris pour le moment et nécessitent une étude approfondie. Et le fait n'est pas que les bons designers ne comprennent pas cela au niveau de l'intuition, il n'est tout simplement pas si facile d'appliquer ces principes dans les méthodes de conception que vous avez étudiées. Les bons esprits ont toujours besoin de tous les outils de conception automatisés que nous avons développés. Les meilleurs esprits seront en mesure d'intégrer ces principes dans les méthodes de conception étudiées pour les rendre accessibles «out of the box» pour tout le monde.

Passons maintenant à un autre exemple et principe, qui m'a permis d'obtenir une solution à un problème important. On m'a donné une équation différentielle



On remarque immédiatement que la valeur de la condition à l'infini est bien le côté droit de l'équation différentielle égale à zéro, figure 20.IX

Mais regardons la question de la stabilité. Si la valeur de y à un point x suffisamment éloigné devient suffisamment grande, alors la valeur de sinh ( y ) devient beaucoup plus grande, la dérivée seconde prend une grande valeur positive et la courbe tire vers plus l'infini. De même, si ytrop petit, alors la courbe tire vers moins l'infini. Et peu importe que nous nous déplacions de gauche à droite ou de droite à gauche. Auparavant, lorsque je suis tombé sur un champ de directions divergent, j'ai utilisé l'astuce évidente: je me suis intégré dans la direction opposée et j'ai obtenu la solution exacte. Mais dans ce cas, nous sommes comme si nous étions sur la crête d'une dune de sable et dès que les deux jambes sont sur la même pente, nous nous effondrons.



Figure 20.IX

J'ai essayé d'utiliser l'expansion dans les séries de puissance, l'expansion dans les séries sans puissance se rapprochant de la courbe d'origine, mais le problème n'a pas disparu, en particulier pour les grandes valeurs de k. Ni moi ni mes amis n'avons pu proposer de solution adéquate. Ensuite, je suis allé voir les directeurs de problème et j'ai commencé par contester la condition aux limites à l'infini, mais il s'est avéré que cette condition était liée à la distance mesurée dans les couches de molécules, et à ce moment-là, tout transistor pratiquement réalisé avait un nombre presque infini de couches. Puis j'ai commencé à contester l'équation, et ils ont de nouveau gagné l'argument, et j'ai dû reculer dans mon bureau et continuer à réfléchir.

Il s'agissait d'une tâche importante liée à la conception et à la compréhension des transistors qui étaient développés à l'époque. J'ai toujours soutenu que si la tâche est importante et correctement posée, je peux trouver une solution. Par conséquent, je n'avais pas le choix, c'était une question d'honneur.

Il m'a fallu quelques jours de réflexion pour réaliser que l'instabilité était la clé d'une méthode adaptée. J'ai construit la solution de l'équation différentielle sur un petit intervalle en utilisant l'analyseur différentiel que j'avais à ce moment-là, et si la solution a grimpé, cela signifie que j'ai choisi trop de coefficient angulaire, si elle a baissé, alors j'ai choisi aussi petite valeur. Ainsi, à petits pas, j'ai marché le long de la crête de la dune, et dès que la décision est tombée d'un côté, j'ai su ce qu'il fallait faire pour revenir sur la crête. Comme vous pouvez le voir, la fierté professionnelle est une bonne aide lorsque vous avez besoin de trouver une solution à une tâche importante dans des conditions difficiles. Comme il était facile de refuser de résoudre ce problème, de se référer au fait qu'il était insoluble,mal posé ou trouver d'autres excuses, mais je crois toujours que les tâches importantes et correctement posées vous permettent d'obtenir de nouvelles informations utiles. Un certain nombre de problèmes liés à la charge d'espace, que j'ai résolus en utilisant des méthodes de calcul, avaient une complexité similaire associée à l'instabilité dans les deux directions.

Avant de vous raconter l'histoire suivante, je veux vous rappeler le test de Rorschach, qui était populaire pendant ma jeunesse. Une goutte d'encre est appliquée sur une feuille de papier, après quoi elle est pliée en deux, et lorsqu'elle est à nouveau déballée, un transfert symétrique d'une forme plutôt aléatoire est obtenu. La séquence de ces transferts est montrée aux sujets qui sont invités à dire ce qu'ils voient. Leurs réponses sont utilisées pour analyser les «caractéristiques» de leur personnalité. De toute évidence, les réponses sont le fruit de leur imagination, car le spot a essentiellement une forme aléatoire. C'est comme regarder des nuages ​​dans le ciel et discuter de leur apparence. Vous ne discutez que des fruits de votre imagination, pas de la réalité, et cela, dans une certaine mesure, ouvre de nouvelles choses sur vous-même, pas sur les nuages. Je suggère que la méthode des taches d'encre ne soit plus utilisée.

Et maintenant passons à l'histoire elle-même. Une fois, mon ami psychologue des Laboratoires Bella a construit une voiture dans laquelle il y avait 12 interrupteurs et deux ampoules - rouge et verte. Vous avez réglé les commutateurs, appuyé sur le bouton, puis un voyant rouge ou vert s'est allumé. Après que le premier sujet ait fait 20 tentatives, il a proposé une théorie sur la façon d'allumer une ampoule verte. Cette théorie a été transmise à la victime suivante, après quoi elle a également eu 20 tentatives pour proposer sa théorie sur la façon d'allumer une ampoule verte. Et ainsi de suite à l'infini. Le but de l'expérience était d'étudier comment les théories se développent.

Mais mon ami, agissant dans son propre style, a connecté les ampoules à une source aléatoire de signaux! Une fois, il s'est plaint à moi que pas un seul participant à l'expérience (et tous étaient des chercheurs de haut niveau aux Laboratoires Bell) a dit qu'il n'y avait pas de modèle. J'ai immédiatement suggéré qu'aucun d'entre eux n'était un spécialiste de la statistique ou de la théorie de l'information - ce sont ces deux types de spécialistes qui connaissent les événements aléatoires. Un test a montré que j'avais raison!

C'est une triste conséquence de votre éducation. Vous avez étudié avec amour comment une théorie est remplacée par une autre, mais vous n'avez pas étudié comment abandonner une belle théorie et accepter le hasard. C'était exactement ce qu'il fallait: être prêt à admettre que la théorie qui vient d'être lue ne convient pas, et qu'il n'y a pas de régularité dans les données, pur hasard!

Je dois m'attarder sur cela plus en détail. Les statisticiens se demandent constamment: "Qu'est-ce que je veux dire en réalité, ou est-ce juste un bruit aléatoire?" Ils ont développé des méthodes de test spéciales pour répondre à cette question. Leurs réponses ne sont pas un oui ou un non définitif, mais oui ou non avec un certain niveau de confiance. Un seuil de confiance de 90% signifie qu'en général sur 10 tentatives, vous ne vous tromperez qu'une seule fois, à condition que toutes les autres hypothèses soient correctes.Dans ce cas, une des deux choses: soit vous avez trouvé quelque chose qui n'est pas (une erreur du premier type) ou vous avez manqué ce que vous cherchiez (une erreur du second type). Beaucoup plus de données sont nécessaires pour obtenir un niveau de confiance de 95%, et la collecte de données peut être très coûteuse à l'heure actuelle. La collecte de données supplémentaires nécessite également du temps supplémentaire et la prise de décision est reportée - c'est une astuce préférée des personnes qui ne veulent pas être responsables de leurs décisions. «Besoin de plus d'informations», vous diront-ils.

J'affirme absolument sérieusement que la plupart des simulations effectuées ne sont rien d'autre qu'un test de Rorschach. Je citerai un excellent praticien de la théorie du contrôle de Jay Forrester: «Du comportement du système, des doutes surgissent qui nécessitent un examen des hypothèses initiales. À partir du processus de traitement des hypothèses initiales sur les parties et le comportement observé de l'ensemble, nous améliorons notre compréhension de la structure et de la dynamique du système. Ce livre est le résultat de plusieurs cycles de ré-études complétés par l'auteur. »

Comment un profane peut-il distinguer cela du test de Rorschach? A-t-il vu quelque chose simplement parce qu'il voulait le voir ou a découvert une nouvelle facette de la réalité? Malheureusement, très souvent, la modélisation contient des ajustements qui vous permettent de "voir uniquement ce que vous voulez". C'est la voie de la moindre résistance, c'est pourquoi la science classique implique un grand nombre de précautions, qui à notre époque sont souvent simplement ignorées.

Pensez-vous que vous faites assez attention à ne pas faire de vœux pieux? Regardons la célèbre étude en double aveugle, qui est une pratique courante en médecine. Au début, les médecins ont constaté que les patients avaient remarqué une amélioration lorsqu'ils pensaient obtenir un nouveau médicament, tandis que les patients du groupe témoin qui savaient qu'ils n'obtiendraient pas de nouveau médicament ne ressentaient aucune amélioration. Après cela, les médecins ont randomisé les groupes et ont commencé à donner à certains patients un placebo afin qu'ils ne puissent pas induire les médecins en erreur. Mais à leur horreur, les médecins ont découvert que les médecins qui savaient qui prenait le médicament et qui ne le faisait pas, ont également constaté des améliorations chez ceux qui l'attendaient et n'ont pas trouvé d'amélioration chez ceux qui ne s'y attendaient pas.En dernier recours, les médecins ont commencé à adopter universellement la méthode d'étude en double aveugle - jusqu'à ce que toutes les données soient collectées, ni les médecins ni les patients ne savent qui prend le nouveau médicament et qui ne le fait pas. À la fin de l'expérience, les statisticiens ouvrent l'enveloppe scellée et analysent. Les médecins qui recherchaient l'honnêteté ont découvert qu'ils n'étaient pas eux-mêmes. Faites-vous la simulation tellement mieux que l'on peut vous faire confiance? Êtes-vous sûr que vous n'avez tout simplement pas trouvé ce que vous aviez tant envie de trouver? L'auto-tromperie est très courante.Faites-vous la simulation tellement mieux que l'on peut vous faire confiance? Êtes-vous sûr que vous n'avez tout simplement pas trouvé ce que vous aviez tant envie de trouver? L'auto-tromperie est très courante.Faites-vous la simulation tellement mieux que l'on peut vous faire confiance? Êtes-vous sûr que vous n'avez tout simplement pas trouvé ce que vous aviez tant envie de trouver? L'auto-tromperie est très courante.

J'ai commencé le chapitre 19 en posant la question, pourquoi tout le monde devrait-il croire que la simulation est effectuée? Maintenant, ce problème est devenu plus évident pour vous. Il n'est pas si facile de répondre à cette question tant que vous n'aurez pas pris beaucoup plus de précautions que d'habitude. Rappelez-vous également que dans votre avenir high-tech, vous représenterez très probablement le côté client de la simulation, et en fonction de ses résultats, vous devrez prendre des décisions. Il n'y a pas d'autre moyen que la modélisation pour obtenir la réponse à la question "Et si ...?". Dans le chapitre 18, j'ai examiné les décisions qui devraient être prises, et ne pas être reportées tout le temps, si l'organisation ne va pas fouiller et dériver sans cesse - je suppose que vous serez parmi ceux qui devront prendre une décision.

La modélisation est nécessaire pour répondre à la question «Et si ...?», Mais en même temps, elle est pleine d'embûches, et vous ne devriez pas faire confiance à ses résultats simplement parce que de grandes ressources humaines et matérielles ont été utilisées pour obtenir de belles impressions ou courbes couleur sur un oscilloscope. Si vous êtes celui qui prend la décision finale, alors toute responsabilité vous incombe. Les décisions collégiales qui conduisent à un brouillage des responsabilités sont rarement de bonnes pratiques - elles sont généralement un compromis médiocre qui n'a le mérite d'aucune des voies possibles. L'expérience m'a appris qu'un boss décisif est bien meilleur qu'un boss bavard. Dans ce cas, vous savez exactement où vous en êtes et pouvez continuer le travail qui doit être fait.

La question "Et si ...?" vous confrontera souvent à l'avenir, vous devez donc gérer les bases et les capacités de modélisation afin d'être prêt à contester les résultats et à comprendre les détails si nécessaire.

À suivre ...

Qui veut aider à la traduction, la mise en page et la publication du livre - écrivez dans un e-mail ou un e-mail personnel magisterludi2016@yandex.ru

Au fait, nous avons également lancé la traduction d'un autre livre cool - "La machine à rêver: l'histoire de la révolution informatique" )