
Je pense qu'un petit non-sens mardi ne fera pas de mal à la semaine de travail. J'ai un passe-temps, dans mon temps libre, j'essaie de comprendre comment pirater l'algorithme de minage de bitcoin, éviter la force brute nonse stupide et trouver une solution au problème de correspondance de hachage avec une consommation d'énergie minimale. Je dois dire tout de suite le résultat, bien sûr, je ne l'ai pas encore atteint, mais néanmoins, pourquoi ne pas exposer par écrit les idées qui naissent dans la tête? Quelque part, ils doivent être placés ...
Malgré le délire des idées ci-dessous, je pense que cet article peut être utile à quelqu'un qui étudie
- Langage C ++ et ses modèles
- certains circuits numériques
- un peu de théorie des probabilités et d'arithmétique probabiliste
- algorithme de hachage bitcoin en détail
Par où commencer?
Peut-être du dernier élément et le plus ennuyeux de cette liste? Patience, alors ce sera plus amusant.
Examinons en détail l'algorithme de calcul de la fonction de hachage du bitcoin. C'est simple F (x) = sha256 (sha256 (x)), où x est les données d'entrée de 80 octets, l'en-tête du bloc avec le numéro de version du bloc, le hachage du bloc précédent, la racine de fusion, l'horodatage, les bits et le nonce. Voici des exemples d'en-têtes de bloc assez récents qui sont passés à la fonction de hachage:
Cet ensemble d'octets est un matériau très précieux, car il n'est souvent pas facile pour les mineurs de comprendre dans quel ordre les octets doivent suivre lors de la formation de l'en-tête, inversant souvent les emplacements des octets bas et hauts (endians).
Ainsi, à partir de l'en-tête du bloc, 80 octets sont considérés comme le hachage sha256, puis à partir du résultat un autre sha256.
L'algorithme sha256 lui-même, si vous regardez différentes sources, se compose généralement de quatre fonctions:
- void sha256_init (SHA256_CTX * ctx);
- void sha256_transform (SHA256_CTX * ctx, const BYTE data []);
- void sha256_update (SHA256_CTX * ctx, const BYTE data [], size_t len);
- void sha256_final (SHA256_CTX * ctx, hachage BYTE []);
La première fonction appelée lors du calcul du hachage est sha256_init (), qui restaure la structure SHA256_CTX. Il n'y a rien de spécial à part huit mots d'état 32 bits, qui sont initialement remplis de mots spéciaux:
void sha256_init(SHA256_CTX *ctx) { ctx->datalen = 0; ctx->bitlen = 0; ctx->state[0] = 0x6a09e667; ctx->state[1] = 0xbb67ae85; ctx->state[2] = 0x3c6ef372; ctx->state[3] = 0xa54ff53a; ctx->state[4] = 0x510e527f; ctx->state[5] = 0x9b05688c; ctx->state[6] = 0x1f83d9ab; ctx->state[7] = 0x5be0cd19; }
Supposons que nous ayons un fichier dont le hachage doit être calculé. Nous lisons le fichier avec des blocs de taille arbitraire et appelons la fonction sha256_update () où nous passons le pointeur sur les données du bloc et la longueur du bloc. La fonction accumule le hachage dans la structure SHA256_CTX dans le tableau d'état:
void sha256_update(SHA256_CTX *ctx, const BYTE data[], size_t len) { uint32_t i; for (i = 0; i < len; ++i) { ctx->data[ctx->datalen] = data[i]; ctx->datalen++; if (ctx->datalen == 64) { sha256_transform(ctx, ctx->data); ctx->bitlen += 512; ctx->datalen = 0; } } }
En soi, sha256_update () appelle la fonction cheval de bataille sha256_transform (), qui accepte déjà des blocs d'une longueur fixe de 64 octets seulement:
#define ROTLEFT(a,b) (((a) << (b)) | ((a) >> (32-(b)))) #define ROTRIGHT(a,b) (((a) >> (b)) | ((a) << (32-(b)))) #define CH(x,y,z) (((x) & (y)) ^ (~(x) & (z))) #define MAJ(x,y,z) (((x) & (y)) ^ ((x) & (z)) ^ ((y) & (z))) #define EP0(x) (ROTRIGHT(x,2) ^ ROTRIGHT(x,13) ^ ROTRIGHT(x,22)) #define EP1(x) (ROTRIGHT(x,6) ^ ROTRIGHT(x,11) ^ ROTRIGHT(x,25)) #define SIG0(x) (ROTRIGHT(x,7) ^ ROTRIGHT(x,18) ^ ((x) >> 3)) #define SIG1(x) (ROTRIGHT(x,17) ^ ROTRIGHT(x,19) ^ ((x) >> 10)) /**************************** VARIABLES *****************************/ static const uint32_t k[64] = { 0x428a2f98,0x71374491,0xb5c0fbcf,0xe9b5dba5,0x3956c25b,0x59f111f1,0x923f82a4,0xab1c5ed5, 0xd807aa98,0x12835b01,0x243185be,0x550c7dc3,0x72be5d74,0x80deb1fe,0x9bdc06a7,0xc19bf174, 0xe49b69c1,0xefbe4786,0x0fc19dc6,0x240ca1cc,0x2de92c6f,0x4a7484aa,0x5cb0a9dc,0x76f988da, 0x983e5152,0xa831c66d,0xb00327c8,0xbf597fc7,0xc6e00bf3,0xd5a79147,0x06ca6351,0x14292967, 0x27b70a85,0x2e1b2138,0x4d2c6dfc,0x53380d13,0x650a7354,0x766a0abb,0x81c2c92e,0x92722c85, 0xa2bfe8a1,0xa81a664b,0xc24b8b70,0xc76c51a3,0xd192e819,0xd6990624,0xf40e3585,0x106aa070, 0x19a4c116,0x1e376c08,0x2748774c,0x34b0bcb5,0x391c0cb3,0x4ed8aa4a,0x5b9cca4f,0x682e6ff3, 0x748f82ee,0x78a5636f,0x84c87814,0x8cc70208,0x90befffa,0xa4506ceb,0xbef9a3f7,0xc67178f2 }; /*********************** FUNCTION DEFINITIONS ***********************/ void sha256_transform(SHA256_CTX *ctx, const BYTE data[]) { uint32_t a, b, c, d, e, f, g, h, i, j, t1, t2, m[64]; for (i = 0, j = 0; i < 16; ++i, j += 4) m[i] = (data[j] << 24) | (data[j + 1] << 16) | (data[j + 2] << 8) | (data[j + 3]); for (; i < 64; ++i) m[i] = SIG1(m[i - 2]) + m[i - 7] + SIG0(m[i - 15]) + m[i - 16]; a = ctx->state[0]; b = ctx->state[1]; c = ctx->state[2]; d = ctx->state[3]; e = ctx->state[4]; f = ctx->state[5]; g = ctx->state[6]; h = ctx->state[7]; for (i = 0; i < 64; ++i) { t1 = h + EP1(e) + CH(e, f, g) + k[i] + m[i]; t2 = EP0(a) + MAJ(a, b, c); h = g; g = f; f = e; e = d + t1; d = c; c = b; b = a; a = t1 + t2; } ctx->state[0] += a; ctx->state[1] += b; ctx->state[2] += c; ctx->state[3] += d; ctx->state[4] += e; ctx->state[5] += f; ctx->state[6] += g; ctx->state[7] += h; }
Lorsque tout le fichier de hachage a été lu et déjà transféré vers la fonction sha256_update (), il ne reste plus qu'à appeler la fonction finale sha256_final (), qui, si la taille du fichier n'était pas un multiple de 64 octets, ajoutera des octets de remplissage supplémentaires, écrit la longueur totale des données à la fin du dernier bloc de données et fera la finale sha256_transform ().
Le résultat du hachage reste dans le tableau d'état.
C'est pour ainsi dire le «haut niveau».
En ce qui concerne le mineur Bitcoin, bien sûr, les développeurs pensent comment considérer plus petit et plus efficace.
C'est simple: l'en-tête ne contient que 80 octets, ce qui n'est pas un multiple de 64 octets. Ainsi, il serait nécessaire que le premier sha256 fasse déjà deux sha256_transform (). Cependant, heureusement pour les mineurs, le nonce du bloc est à la fin de l'en-tête, donc le premier sha256_transform () ne peut être exécuté qu'une seule fois - ce sera ce qu'on appelle le midstate. Ensuite, le mineur passe par toutes les options nonse, qui sont 4 milliards, 2 ^ 32 et les substitue dans le champ correspondant à la deuxième sha256_transform (). Cette transformation termine la première fonction sha256. Son résultat est huit mots de 32 bits, soit 32 octets. Il est facile de trouver sha256 à partir d'eux - le dernier sha256_transform () est appelé, et tout est prêt. Notez que les données d'entrée sont inférieures de 32 octets aux 64 octets nécessaires pour sha256_transform (). Encore une fois, le bloc sera rempli de zéros et la longueur du bloc sera entrée à la fin.
Au total, il n'y a que trois appels à sha256_transform () dont le premier doit être lu une seule fois pour calculer le midstate.
J'ai essayé d'étendre toutes les manipulations de données qui se produisent lors du calcul du hachage de l'en-tête d'un bloc bitcoin en une seule fonction, afin qu'il soit clair comment tout le calcul se produit spécifiquement pour bitcoin et c'est ce qui s'est passé:
J'ai implémenté cette fonction en tant que modèle c ++, elle peut fonctionner non seulement sur des mots 32 bits, par exemple uint32_t, mais également sur des mots d'un type différent "T" de la même manière. J'ai ici et l'état sha256 est stocké comme un tableau de type "T" et sha256_transform () est appelé avec un pointeur de paramètre vers un tableau de type "T" et le résultat est retourné le même. La fonction de transformation est désormais également sous la forme d'un modèle c ++:
template <typename T> T ror32(T word, unsigned int shift) { return (word >> shift) | (word << (32 - shift)); } template <typename T> T Ch(T x, T y, T z) { return z ^ (x & (y ^ z)); } template<typename T> T Maj(T x, T y, T z) { return (x & y) | (z & (x | y)); } #define e0(x) (ror32(x, 2) ^ ror32(x,13) ^ ror32(x,22)) #define e1(x) (ror32(x, 6) ^ ror32(x,11) ^ ror32(x,25)) #define s0(x) (ror32(x, 7) ^ ror32(x,18) ^ (x >> 3)) #define s1(x) (ror32(x,17) ^ ror32(x,19) ^ (x >> 10)) unsigned int ntohl(unsigned int in) { return ((in & 0xff) << 24) | ((in & 0xff00) << 8) | ((in & 0xff0000) >> 8) | ((in & 0xff000000) >> 24); } template <typename T> void LOAD_OP(int I, T *W, const u8 *input) { //W[I] = /*ntohl*/ (((u32*)(input))[I]); W[I] = ntohl(((u32*)(input))[I]); //W[I] = (input[3] << 24) | (input[2] << 16) | (input[1] << 8) | (input[0]); } template <typename T> void BLEND_OP(int I, T *W) { W[I] = s1(W[I - 2]) + W[I - 7] + s0(W[I - 15]) + W[I - 16]; } template <typename T> void sha256_transform(T *state, const T *input) { T a, b, c, d, e, f, g, h, t1, t2; TW[64]; int i; /* load the input */ for (i = 0; i < 16; i++) // MJ input is cast to u32* so this processes 16 DWORDS = 64 bytes W[i] = input[i]; /* now blend */ for (i = 16; i < 64; i++) BLEND_OP(i, W); /* load the state into our registers */ a = state[0]; b = state[1]; c = state[2]; d = state[3]; e = state[4]; f = state[5]; g = state[6]; h = state[7]; // t1 = h + e1(e) + Ch(e, f, g) + 0x428a2f98 + W[0]; t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2; t1 = g + e1(d) + Ch(d, e, f) + 0x71374491 + W[1]; t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2; t1 = f + e1(c) + Ch(c, d, e) + 0xb5c0fbcf + W[2]; t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2; t1 = e + e1(b) + Ch(b, c, d) + 0xe9b5dba5 + W[3]; t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2; t1 = d + e1(a) + Ch(a, b, c) + 0x3956c25b + W[4]; t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2; t1 = c + e1(h) + Ch(h, a, b) + 0x59f111f1 + W[5]; t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2; t1 = b + e1(g) + Ch(g, h, a) + 0x923f82a4 + W[6]; t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2; t1 = a + e1(f) + Ch(f, g, h) + 0xab1c5ed5 + W[7]; t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2; t1 = h + e1(e) + Ch(e, f, g) + 0xd807aa98 + W[8]; t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2; t1 = g + e1(d) + Ch(d, e, f) + 0x12835b01 + W[9]; t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2; t1 = f + e1(c) + Ch(c, d, e) + 0x243185be + W[10]; t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2; t1 = e + e1(b) + Ch(b, c, d) + 0x550c7dc3 + W[11]; t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2; t1 = d + e1(a) + Ch(a, b, c) + 0x72be5d74 + W[12]; t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2; t1 = c + e1(h) + Ch(h, a, b) + 0x80deb1fe + W[13]; t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2; t1 = b + e1(g) + Ch(g, h, a) + 0x9bdc06a7 + W[14]; t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2; t1 = a + e1(f) + Ch(f, g, h) + 0xc19bf174 + W[15]; t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2; t1 = h + e1(e) + Ch(e, f, g) + 0xe49b69c1 + W[16]; t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2; t1 = g + e1(d) + Ch(d, e, f) + 0xefbe4786 + W[17]; t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2; t1 = f + e1(c) + Ch(c, d, e) + 0x0fc19dc6 + W[18]; t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2; t1 = e + e1(b) + Ch(b, c, d) + 0x240ca1cc + W[19]; t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2; t1 = d + e1(a) + Ch(a, b, c) + 0x2de92c6f + W[20]; t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2; t1 = c + e1(h) + Ch(h, a, b) + 0x4a7484aa + W[21]; t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2; t1 = b + e1(g) + Ch(g, h, a) + 0x5cb0a9dc + W[22]; t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2; t1 = a + e1(f) + Ch(f, g, h) + 0x76f988da + W[23]; t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2; t1 = h + e1(e) + Ch(e, f, g) + 0x983e5152 + W[24]; t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2; t1 = g + e1(d) + Ch(d, e, f) + 0xa831c66d + W[25]; t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2; t1 = f + e1(c) + Ch(c, d, e) + 0xb00327c8 + W[26]; t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2; t1 = e + e1(b) + Ch(b, c, d) + 0xbf597fc7 + W[27]; t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2; t1 = d + e1(a) + Ch(a, b, c) + 0xc6e00bf3 + W[28]; t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2; t1 = c + e1(h) + Ch(h, a, b) + 0xd5a79147 + W[29]; t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2; t1 = b + e1(g) + Ch(g, h, a) + 0x06ca6351 + W[30]; t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2; t1 = a + e1(f) + Ch(f, g, h) + 0x14292967 + W[31]; t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2; t1 = h + e1(e) + Ch(e, f, g) + 0x27b70a85 + W[32]; t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2; t1 = g + e1(d) + Ch(d, e, f) + 0x2e1b2138 + W[33]; t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2; t1 = f + e1(c) + Ch(c, d, e) + 0x4d2c6dfc + W[34]; t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2; t1 = e + e1(b) + Ch(b, c, d) + 0x53380d13 + W[35]; t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2; t1 = d + e1(a) + Ch(a, b, c) + 0x650a7354 + W[36]; t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2; t1 = c + e1(h) + Ch(h, a, b) + 0x766a0abb + W[37]; t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2; t1 = b + e1(g) + Ch(g, h, a) + 0x81c2c92e + W[38]; t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2; t1 = a + e1(f) + Ch(f, g, h) + 0x92722c85 + W[39]; t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2; t1 = h + e1(e) + Ch(e, f, g) + 0xa2bfe8a1 + W[40]; t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2; t1 = g + e1(d) + Ch(d, e, f) + 0xa81a664b + W[41]; t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2; t1 = f + e1(c) + Ch(c, d, e) + 0xc24b8b70 + W[42]; t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2; t1 = e + e1(b) + Ch(b, c, d) + 0xc76c51a3 + W[43]; t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2; t1 = d + e1(a) + Ch(a, b, c) + 0xd192e819 + W[44]; t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2; t1 = c + e1(h) + Ch(h, a, b) + 0xd6990624 + W[45]; t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2; t1 = b + e1(g) + Ch(g, h, a) + 0xf40e3585 + W[46]; t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2; t1 = a + e1(f) + Ch(f, g, h) + 0x106aa070 + W[47]; t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2; t1 = h + e1(e) + Ch(e, f, g) + 0x19a4c116 + W[48]; t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2; t1 = g + e1(d) + Ch(d, e, f) + 0x1e376c08 + W[49]; t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2; t1 = f + e1(c) + Ch(c, d, e) + 0x2748774c + W[50]; t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2; t1 = e + e1(b) + Ch(b, c, d) + 0x34b0bcb5 + W[51]; t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2; t1 = d + e1(a) + Ch(a, b, c) + 0x391c0cb3 + W[52]; t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2; t1 = c + e1(h) + Ch(h, a, b) + 0x4ed8aa4a + W[53]; t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2; t1 = b + e1(g) + Ch(g, h, a) + 0x5b9cca4f + W[54]; t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2; t1 = a + e1(f) + Ch(f, g, h) + 0x682e6ff3 + W[55]; t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2; t1 = h + e1(e) + Ch(e, f, g) + 0x748f82ee + W[56]; t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2; t1 = g + e1(d) + Ch(d, e, f) + 0x78a5636f + W[57]; t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2; t1 = f + e1(c) + Ch(c, d, e) + 0x84c87814 + W[58]; t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2; t1 = e + e1(b) + Ch(b, c, d) + 0x8cc70208 + W[59]; t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2; t1 = d + e1(a) + Ch(a, b, c) + 0x90befffa + W[60]; t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2; t1 = c + e1(h) + Ch(h, a, b) + 0xa4506ceb + W[61]; t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2; t1 = b + e1(g) + Ch(g, h, a) + 0xbef9a3f7 + W[62]; t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2; t1 = a + e1(f) + Ch(f, g, h) + 0xc67178f2 + W[63]; t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2; state[0] += a; state[1] += b; state[2] += c; state[3] += d; state[4] += e; state[5] += f; state[6] += g; state[7] += h; }
L'utilisation des fonctions de modèle C ++ est pratique dans la mesure où je peux calculer le hachage dont j'ai besoin à partir de données régulières et obtenir le résultat habituel:
const uint8_t header[] = { 0x02,0x00,0x00,0x00, 0x17,0x97,0x5b,0x97,0xc1,0x8e,0xd1,0xf7, 0xe2,0x55,0xad,0xf2,0x97,0x59,0x9b,0x55, 0x33,0x0e,0xda,0xb8,0x78,0x03,0xc8,0x17, 0x01,0x00,0x00,0x00,0x00,0x00,0x00,0x00, 0x8a,0x97,0x29,0x5a,0x27,0x47,0xb4,0xf1, 0xa0,0xb3,0x94,0x8d,0xf3,0x99,0x03,0x44, 0xc0,0xe1,0x9f,0xa6,0xb2,0xb9,0x2b,0x3a, 0x19,0xc8,0xe6,0xba, 0xdc,0x14,0x17,0x87, 0x35,0x8b,0x05,0x53, 0x53,0x5f,0x01,0x19, 0x48,0x75,0x08,0x33 }; uint32_t test_nonce = 0x48750833; uint32_t result[8]; full_btc_hash(header, test_nonce, result); uint8_t* presult = (uint8_t * )result; for (int i = 0; i < 32; i++) printf("%02X ", presult[i]);
Il s'avère:
92 98 2A 50 91 FA BD 42 97 8A A5 2D CD C9 36 28 02 4A DD FE E0 67 A4 78 00 00 00 00 00 00 00 00 00
À la fin du hachage, il y a beaucoup de zéros, un beau hachage, un bingo, etc.
Et maintenant, je peux transmettre non pas des données uint32_t ordinaires à cette fonction de hachage, mais ma classe C ++ spéciale, qui redéfinira toute l'arithmétique.
Oui oui Je vais appliquer des mathématiques probabilistes «alternatives».
Je l'ai inventé moi-même, je l'ai réalisé, je l'ai vécu moi-même. Cela ne semble pas très bien fonctionner. Une plaisanterie. Ça devrait marcher. Peut-être que je ne suis pas le premier que j'essaie de lancer.
Passons maintenant au plus intéressant.
Toute l'arithmétique en électronique numérique est exécutée comme des opérations sur des bits, et elle est strictement définie par les opérations ET, OU, NON, OU EXCLUSIF. Eh bien, nous savons tous ce que sont les tables de vérité en algèbre booléenne.
Je suggère d'ajouter un peu d'incertitude aux calculs, les rendant probabilistes.
Laissez chaque bit du mot avoir non seulement les valeurs ZERO et ONE possibles, mais aussi toutes les valeurs intermédiaires! Je propose de considérer la valeur d'un bit comme la probabilité d'un événement qui peut ou non se produire. Si toutes les données initiales sont connues de manière fiable, le résultat est fiable. Et si certaines données manquent un peu, le résultat se révélera avec une certaine probabilité.
En fait, supposons qu'il existe deux événements indépendants «a» et «b», dont la probabilité d'occurrence est naturellement de zéro à un, respectivement, Pa et Pb. Quelle est la probabilité que des événements se produisent simultanément? Je suis sûr que chacun de nous n'hésitera pas à répondre P = Pa * Pb et c'est la bonne réponse!
Le graphique 3D d'une telle fonction ressemblera à ceci (de deux points de vue différents):
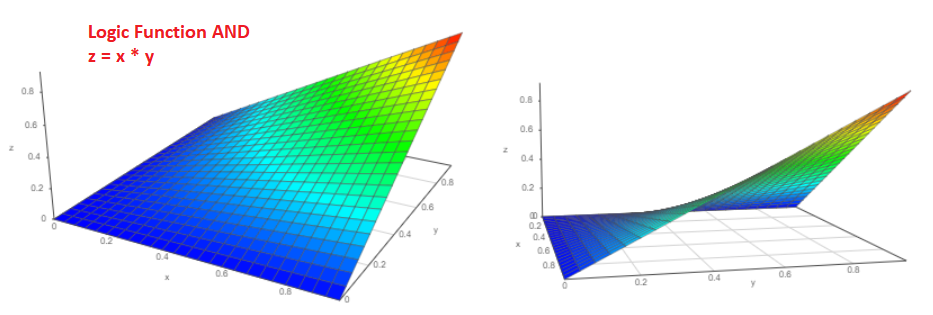
Et quelle est la probabilité que l'événement Pa ou l'événement Pb se produise?
Probabilité P = Pa + Pb-Pa * Pb. Le graphe de fonction est comme ceci:
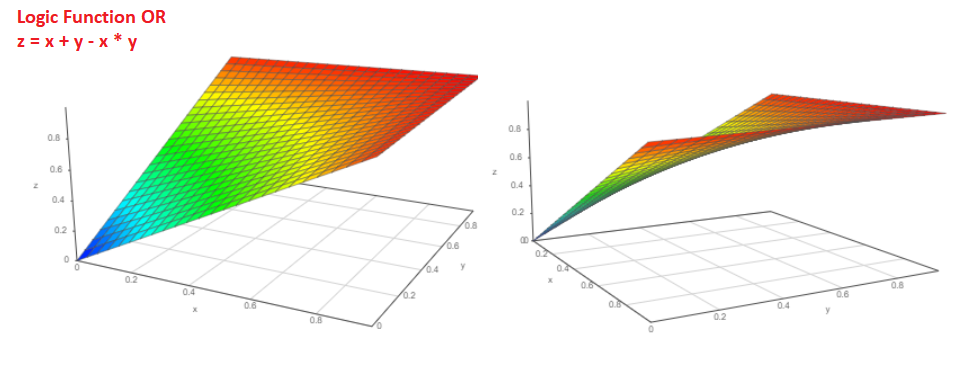
Et si nous connaissons la probabilité que l'événement Pa se produise, quelle est la probabilité que l'événement ne se produise pas?
P = 1 - Pa.
Faisons maintenant une hypothèse. Imaginez que nous ayons des éléments logiques qui calculent la probabilité d'un événement de sortie, connaissant la probabilité d'événements d'entrée:
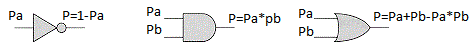
Avoir de tels éléments logiques peut facilement les rendre plus complexes, par exemple, exclusifs ou XOR:
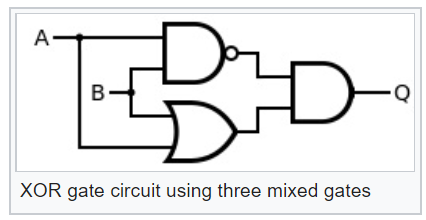
Maintenant, en regardant le diagramme de cet élément logique XOR, nous pouvons comprendre quelle sera la probabilité de l'événement à la sortie du XOR probabiliste:
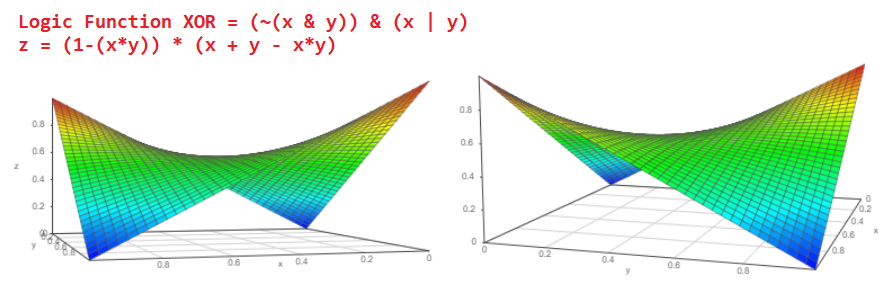
Mais ce n'est pas tout. Nous connaissons la logique typique d'un additionneur complet et découvrons comment un additionneur multi-bits est fabriqué à partir d'un additionneur complet:
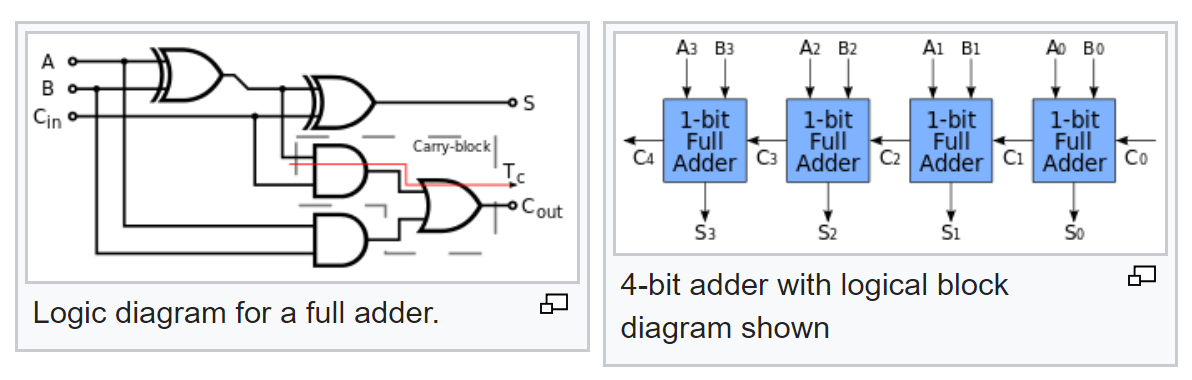
Alors maintenant, selon son schéma, nous pouvons maintenant calculer les probabilités de signaux à sa sortie, avec des probabilités connues de signaux à l'entrée.
Ainsi, je peux implémenter en c ++ ma propre classe "32 bits" (je l'appellerai x32) avec une arithmétique probabiliste, redéfinir toutes les opérations nécessaires pour sha256 comme AND, OR, XOR, ADD et les décalages dans cette classe. La classe stockera 32 bits à l'intérieur, mais chaque bit est un nombre à virgule flottante. Chaque opération logique ou arithmétique sur un tel nombre de 32 bits calculera la probabilité de la valeur de chaque bit avec des paramètres d'entrée connus ou peu connus d'une opération logique ou arithmétique.
Prenons un exemple très simple qui utilise mes mathématiques probabilistes:
typedef std::numeric_limits< double > dbl; int main(int argc, char *argv[]) { cout.precision(dbl::max_digits10); x32 a = 0xaabbccdd; x32 b = 0x12345678; <b>
Dans cet exemple, deux nombres 32 bits sont ajoutés.
Alors que la chaîne est b.setBit (4, 0,75); Le résultat de l'addition est commenté exactement prévisible et prédéterminé, car toutes les données d'entrée pour l'addition sont connues. Le programme imprime ceci sur la console:
result = 0xbcf02355 bit0 = 1 bit1 = 0 bit2 = 1 bit3 = 0 bit4 = 1 bit5 = 0 bit6 = 1 bit7 = 0 bit8 = 1 bit9 = 1 bit10 = 0 bit11 = 0 bit12 = 0 bit13 = 1 bit14 = 0 bit15 = 0 bit16 = 0 bit17 = 0 bit18 = 0 bit19 = 0 bit20 = 1 bit21 = 1 bit22 = 1 bit23 = 1 bit24 = 0 bit25 = 0 bit26 = 1 bit27 = 1 bit28 = 1 bit29 = 1 bit30 = 0 bit31 = 1
Si je décommente la ligne b.setBit (4, 0,75); alors en faisant cela, je dis au programme: "ajoutez-moi ces deux nombres, mais je ne connais pas vraiment la valeur du bit 4 du deuxième argument, je pense que c'est un avec une probabilité de 0,75".
Ensuite, l'addition se produit, comme il se doit, avec un calcul complet des probabilités des signaux de sortie, c'est-à-dire des bits:
bit not stable bit not stable bit not stable result = 0xbcf02305 bit0 = 1 bit1 = 0 bit2 = 1 bit3 = 0 bit4 = 0.75 bit5 = 0.1875 bit6 = 0.8125 bit7 = 0 bit8 = 1 bit9 = 1 bit10 = 0 bit11 = 0 bit12 = 0 bit13 = 1 bit14 = 0 bit15 = 0 bit16 = 0 bit17 = 0 bit18 = 0 bit19 = 0 bit20 = 1 bit21 = 1 bit22 = 1 bit23 = 1 bit24 = 0 bit25 = 0 bit26 = 1 bit27 = 1 bit28 = 1 bit29 = 1 bit30 = 0 bit31 = 1
Étant donné que les données d'entrée n'étaient pas très connues, le résultat n'est pas très connu. De plus, ce qui peut être calculé de manière fiable est considéré comme fiable. Ce qui ne peut pas être compté est considéré avec probabilité.
Maintenant que j'ai une merveilleuse classe c ++ 32 bits pour l'arithmétique floue, je peux passer des tableaux de variables de type x32 à la fonction full_btc_hash () dans le modèle et obtenir un résultat de hachage estimé probabiliste.
Certaines des implémentations de classe x32 sont: #pragma once #include <string> #include <list> #include <iostream> #include <utility> #include <stdint.h> #include <vector> #include <limits> using namespace std; #include <boost/math/constants/constants.hpp> #include <boost/multiprecision/cpp_dec_float.hpp> using boost::multiprecision::cpp_dec_float_50; //typedef double MY_FP; typedef cpp_dec_float_50 MY_FP; class x32 { public: x32(); x32(uint32_t n); void init(MY_FP val); void init(double* pval); void setBit(int i, MY_FP val) { bvi[i] = val; }; ~x32() {}; x32 operator|(const x32& right); x32 operator&(const x32& right); x32 operator^(const x32& right); x32 operator+(const x32& right); x32& x32::operator+=(const x32& right); x32 operator~(); x32 operator<<(const unsigned int& right); x32 operator>>(const unsigned int& right); void print(); uint32_t get32(); MY_FP get_bvi(uint32_t idx) { return bvi[idx]; }; private: MY_FP not(MY_FP a); MY_FP and(MY_FP a, MY_FP b); MY_FP or (MY_FP a, MY_FP b); MY_FP xor(MY_FP a, MY_FP b); MY_FP bvi[32]; //bit values }; #include "stdafx.h" #include "x32.h" x32::x32() { for (int i = 0; i < 32; i++) { bvi[i] = 0.0; } } x32::x32(uint32_t n) { for (int i = 0; i < 32; i++) { bvi[i] = (n&(1 << i)) ? 1.0 : 0.0; } } void x32::init(MY_FP val) { for (int i = 0; i < 32; i++) { bvi[i] = val; } } void x32::init(double* pval) { for (int i = 0; i < 32; i++) { bvi[i] = pval[i]; } } x32 x32::operator<<(const unsigned int& right) { x32 t; for (int i = 31; i >= 0; i--) { if (i < right) { t.bvi[i] = 0.0; } else { t.bvi[i] = bvi[i - right]; } } return t; } x32 x32::operator>>(const unsigned int& right) { x32 t; for (unsigned int i = 0; i < 32; i++) { if (i >= (32 - right)) { t.bvi[i] = 0; } else { t.bvi[i] = bvi[i + right]; } } return t; } MY_FP x32::not(MY_FP a) { return 1.0 - a; } MY_FP x32::and(MY_FP a, MY_FP b) { return a * b; } MY_FP x32::or(MY_FP a, MY_FP b) { return a + b - a * b; } MY_FP x32::xor (MY_FP a, MY_FP b) { //(~(A & B)) & (A | B) return and( not( and(a,b) ) , or(a,b) ); } x32 x32::operator|(const x32& right) { x32 t; for (int i = 0; i < 32; i++) { t.bvi[i] = or ( bvi[i], right.bvi[i] ); } return t; } x32 x32::operator&(const x32& right) { x32 t; for (int i = 0; i < 32; i++) { t.bvi[i] = and (bvi[i], right.bvi[i]); } return t; } x32 x32::operator~() { x32 t; for (int i = 0; i < 32; i++) { t.bvi[i] = not(bvi[i]); } return t; } x32 x32::operator^(const x32& right) { x32 t; for (int i = 0; i < 32; i++) { t.bvi[i] = xor (bvi[i], right.bvi[i]); } return t; } x32 x32::operator+(const x32& right) { x32 r; r.bvi[0] = xor (bvi[0], right.bvi[0]); MY_FP cout = and (bvi[0], right.bvi[0]); for (unsigned int i = 1; i < 32; i++) { MY_FP xor_a_b = xor (bvi[i], right.bvi[i]); r.bvi[i] = xor( xor_a_b, cout ); MY_FP and1 = and (bvi[i], right.bvi[i]); MY_FP and2 = and (xor_a_b, cout); cout = or (and1,and2); } return r; } x32& x32::operator+=(const x32& right) { MY_FP cout = and (bvi[0], right.bvi[0]); bvi[0] = xor (bvi[0], right.bvi[0]); for (unsigned int i = 1; i < 32; i++) { MY_FP xor_a_b = xor (bvi[i], right.bvi[i]); MY_FP and1 = and (bvi[i], right.bvi[i]); MY_FP and2 = and (xor_a_b, cout); bvi[i] = xor (xor_a_b, cout); cout = or (and1, and2); } return *this; } void x32::print() { for (int i = 0; i < 32; i++) { cout << bvi[i] << "\n"; } } uint32_t x32::get32() { uint32_t r = 0; for (int i = 0; i < 32; i++) { if (bvi[i] == 1.0) r = r | (1 << i); else if (bvi[i] == 0.0) { //ok } else { //oops.. cout << "bit not stable\n"; } } return r; }
À quoi tout cela sert-il?
Le mineur Bitcoin ne sait pas à l'avance quelle valeur sélectionner 32x nonce. Le mineur est obligé d'itérer sur les 4 milliards d'entre eux afin de compter le hachage jusqu'à ce qu'il devienne «beau», jusqu'à ce que la valeur du hachage devienne inférieure à l'objectif.
L'arithmétique probabiliste floue vous permet théoriquement de vous débarrasser de la recherche exhaustive.
Oui, je ne connais pas initialement la signification de tous les bits nonse requis. Si je ne les connais pas, qu'il n'y ait pas de merde - la probabilité initiale de non-bits est de 0,5. Même dans ce scénario, je peux calculer la probabilité de bits de hachage de sortie. Quelque part quelque chose, ils se révèlent également environ 0,5 plus ou moins un demi-sou.
Cependant, je peux maintenant changer un seul bit nonse de 0,5 à 0,9 ou à 0,1 ou à 1,0 et voir comment la valeur de probabilité de la valeur du signal de chaque bit de la fonction de hachage sur la sortie change. Maintenant, j'ai beaucoup plus d'informations sur l'évaluation. Je peux maintenant sentir chaque bit nonse d'entrée individuellement et voir où la probabilité du signal se décale sur chacun des bits de sortie de la fonction de hachage.Par exemple, voici un fragment qui considère une fonction de hachage avec des bits nonse complètement inconnus, lorsque la probabilité de sa valeur de bit est 0,5 et le deuxième calcul, lorsque nous supposons que la valeur du bit nonce [0] = 0,9: typedef std::numeric_limits< double > dbl; int main(int argc, char *argv[]) { cout.precision(dbl::max_digits10);
La fonction de classe x32 :: get_bvi () renvoie la probabilité de la valeur binaire de ce nombre.Nous calculons et voyons que si vous modifiez la valeur du bit nonce [0] de 0,5 à 0,9, alors certains bits du hachage de sortie se sont à peine inclinés vers le haut et d'autres à peine inclinés: 0.44525679540883948 0.44525679540840074 0.55268174813167364 0.5526817481315932 0.57758654725359399 0.57758654725360606 0.49595026978928474 0.49595026978930477 0.57118578561406703 0.57118578561407746 0.53237003739057907 0.5323700373905661 0.57269859374138096 0.57269859374138162 0.57631236396381141 0.5763123639638157 0.47943176373960149 0.47943176373960219 0.54955992675177704 0.5495599267517755 0.53321116270879686 0.53321116270879733 0.57294025883744952 0.57294025883744984 0.53131857821387693 0.53131857821387655 0.57253530821899101 0.57253530821899102 0.50661432403287194 0.50661432403287198 0.57149419848354913 0.57149419848354916 0.53220327148366491 0.53220327148366487 0.57268927270412251 0.57268927270412251 0.57632130426913003 0.57632130426913005 0.57233970084776142 0.57233970084776143 0.56824728628552812 0.56824728628552813 0.45247155441889921 0.45247155441889922 0.56875940568326509 0.56875940568326509 0.57524323439326321 0.57524323439326321 0.57587726902392535 0.57587726902392535 0.57597043124557292 0.57597043124557292 0.52847748894672118 0.52847748894672118 0.54512141953055808 0.54512141953055808 0.57362254577539695 0.57362254577539695 0.53082194129771177 0.53082194129771177 0.54404489702929382 0.54404489702929382 0.54065386336136847 0.54065386336136847
Une sorte de souffle, un changement à peine perceptible dans la probabilité d'une sortie à 10m après la virgule. Eh bien, néanmoins ... vous pouvez essayer de construire quelques hypothèses à ce sujet. Cela se passe magnifiquement, non?Par ailleurs, si les bits d'entrée du nonse d'entrée sont initialisés avec les valeurs de probabilité nécessaires et correctes, comme ceci: double nonce_bits[32]; for (int i = 0; i < 32; i++) nonce_bits[i] = (real_nonce32&(1 << i)) ? 1.0 : 0.0; x32 nonce_x32; nonce_x32.init(nonce_bits); full_btc_hash(strxx, nonce_x32, result_x32);
puis en calculant le hachage probabiliste, nous obtenons le résultat logique correct - un «beau» hachage en sortie, bingo.Donc, avec les mathématiques, tout est là.Reste à apprendre à analyser le souffle de la brise ... et le hash est cassé.Cela ressemble à un non-sens, mais c'est un non-sens - et j'ai prévenu au tout début.Autres matériaux utiles:- Minim Bitcoin avec papier et stylo.
- Est-il possible de calculer des bitcoins plus rapidement, plus facilement ou plus facilement?
- Comment ai-je fait un mineur blakecoin
- Mineur FPGA Bitcoin sur Mars Rover Board 3
- FPGA Miner avec algorithme Blake