Implémentation FPGA de la FFT entière

Bonjour à tous!

Une fois, les clients m'ont demandé si j'avais de la FFT entière dans mes projets, à laquelle j'ai toujours répondu que cela avait déjà été fait par d'autres sous la forme de cœurs IP prêts à l'emploi, bien que courbes, mais gratuits (Altera / Xilinx) - prenez-le et utilisez-le. Cependant, ces cœurs ne sont pas optimaux , ont un ensemble de «fonctionnalités» et nécessitent un raffinement supplémentaire. À cet égard, après avoir pris d'autres vacances prévues, que je ne voulais pas passer médiocres, j'ai commencé à implémenter le noyau configurable de la FFT entière.


_{KDPV (processus de débogage des erreurs de débordement de données)}

Dans l'article, je veux vous dire par quelles méthodes et moyens les opérations mathématiques sont réalisées lors du calcul de la transformée de Fourier rapide dans un format entier sur des cristaux FPGA modernes. La base de toute FFT est un nœud appelé «papillon». Le papillon met en œuvre des opérations mathématiques - addition, multiplication et soustraction. C'est sur l'implémentation du "papillon" et de ses nœuds finis que l'histoire se déroulera en premier. Basé sur les familles FPGA Xilinx modernes - ce sont les séries Ultrascale et Ultrascale +, ainsi que les anciennes séries 6- (Virtex) et 7- (Artix, Kintex, Virtex) sont affectées. Les anciennes séries de projets modernes ne sont pas intéressantes en 2018. Le but de l'article est de révéler les caractéristiques de la mise en œuvre de noyaux personnalisés de traitement de signal numérique en utilisant l'exemple FFT.

Présentation

Ce n'est un secret pour personne que les algorithmes pour prendre la FFT sont fermement ancrés dans la vie des ingénieurs en traitement du signal numérique, et donc cet outil est constamment nécessaire. Les principaux fabricants de FPGA tels que Altera / Xilinx ont déjà des cœurs FFT / IFFT configurables flexibles, mais ils ont un certain nombre de limitations et de fonctionnalités, et j'ai donc dû utiliser ma propre expérience plus d'une fois. Donc, cette fois, j'ai dû implémenter une FFT dans un format entier selon le schéma Radix-2 sur le FPGA. Dans mon dernier article, j'ai déjà fait de la FFT au format virgule flottante, et de là, vous savez que l'algorithme à double parallélisme est utilisé pour implémenter la FFT, c'est-à-dire que le noyau peut traiter deux échantillons complexes à la même fréquence . Il s'agit d'une fonctionnalité FFT clé qui n'est pas disponible dans les noyaux prêts à l'emploi FFT Xilinx.

Exemple: il est nécessaire de développer un nœud FFT effectuant un fonctionnement continu du flux d'entrée de nombres complexes à une fréquence de 800 MHz. Le cœur de Xilinx ne tirera pas cela (les fréquences d'horloge de traitement réalisables dans les FPGA modernes sont de l'ordre de 300 à 400 MHz), ou il faudra décimer le flux d'entrée d'une manière ou d'une autre. Le noyau personnalisé vous permet de synchroniser deux échantillons d'entrée à une fréquence de 400 MHz sans intervention préalable, au lieu d'un seul échantillon à 800 MHz. Un autre inconvénient du noyau Xilinx FFT est l'incapacité à accepter le flux d'entrée dans l'ordre inverse des bits . À cet égard, une énorme ressource de mémoire de puce FPGA est dépensée pour réorganiser les données dans un ordre normal. Pour les tâches de convolution rapide de signaux, lorsque deux nœuds FFT se tiennent l'un derrière l'autre, cela peut devenir un moment critique, c'est-à-dire que la tâche ne réside tout simplement pas dans la puce FPGA sélectionnée. Le noyau FFT personnalisé vous permet de recevoir des données dans l'ordre normal à l'entrée et de les produire en mode bit-reverse, tandis que le noyau de la FFT inverse - au contraire, reçoit les données dans l'ordre bit-reverse et les sort en mode normal. Deux tampons pour la permutation des données sont enregistrés à la fois !!!

Étant donné que la plupart des éléments de cet article peuvent chevaucher le précédent , j'ai décidé de me concentrer sur le thème des opérations mathématiques au format entier sur FPGA pour la mise en œuvre de la FFT.

Paramètres du noyau FFT

• NFFT - nombre de papillons (longueur FFT),
• DATA_WIDTH - profondeur de bits des données d'entrée (4-32),
• TWDL_WIDTH - profondeur de bits des facteurs de rotation (8-27).
• SERIES - définit la famille FPGA sur laquelle la FFT est implémentée («NEW» - Ultrascale, «OLD» - 6/7 Xilinx FPGA series).

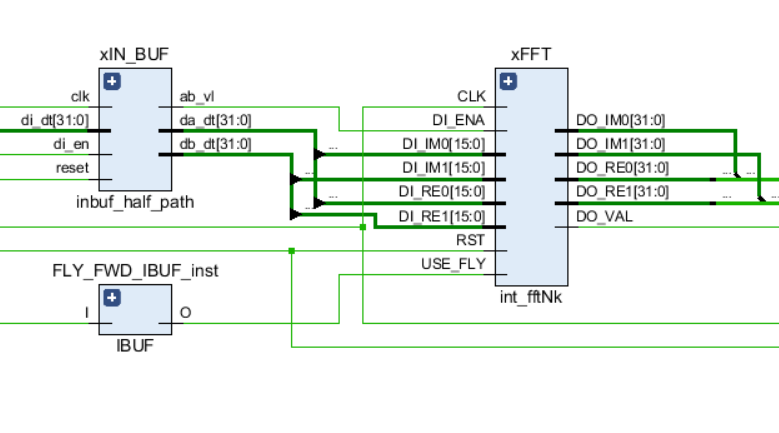
Comme toutes les autres liaisons du circuit, la FFT possède des ports de contrôle d'entrée - un signal d'horloge et une réinitialisation, ainsi que des ports de données d'entrée et de sortie. De plus, le signal USE_FLY est utilisé dans le noyau, ce qui vous permet de désactiver dynamiquement les papillons FFT pour les processus de débogage ou de voir le flux d'entrée d'origine.

Le tableau ci-dessous montre la quantité de ressources FPGA utilisées, en fonction de la longueur de la FFT NFFT pour DATA_WIDTH = 16 et deux bits TWDL_WIDTH = 16 et 24 bits.



Le noyau à NFFT = 64K est stable à la fréquence de traitement FREQ = 375 MHz sur un cristal Kintex-7 (410T).

Structure du projet

Le graphique schématique du nœud FFT est illustré dans la figure suivante:


Pour faciliter la compréhension des fonctionnalités de certains composants, je vais donner une liste des fichiers de projet et leur brève description dans un ordre hiérarchique:

• Noyaux FFT:
  
  • int_fftNk - Nœud FFT, circuit Radix-2, décimation de fréquence (DIF), le flux d'entrée est normal, le flux de sortie est inversé.
  • int_ifftNk - Noeud OBPF , circuit Radix-2, décimation temporelle (DIT), le flux d'entrée est inversé, le flux de sortie est normal.
• Papillons:
  
  
  • int_dif2_fly - papillon Radix-2, décimation en fréquence,
  • int_dit2_fly - papillon Radix-2, décimation dans le temps,
• Multiplicateurs complexes:
  
  
  • int_cmult_dsp48 - multiplicateur configurable général, comprend:
  • int_cmult18x25_dsp48 - multiplicateur pour de faibles profondeurs de bits des données et des facteurs de rotation,
  • int_cmult_dbl18_dsp48 - multiplicateur doublé, largeur de bits des facteurs de rotation jusqu'à 18 bits,
  • int_cmult_dbl35_dsp48 - multiplicateur doublé, largeur de bits des facteurs de rotation jusqu'à 25 * bits,
  • int_cmult_trpl18_dsp48 - triple multiplicateur, la capacité des facteurs de rotation jusqu'à 18 bits,
  • int_cmult_trpl52_dsp48 - triple multiplicateur, la capacité des facteurs de rotation jusqu'à 25 * bits,
• Multiplicateurs:
  
  
  • mlt42x18_dsp48e1 - un multiplicateur avec des bits d'opérandes jusqu'à 42 et 18 bits basés sur DSP48E1,
  • mlt59x18_dsp48e1 - multiplicateur avec des bits d'opérande jusqu'à 59 et 18 bits basés sur DSP48E1,
  • mlt35x25_dsp48e1 - un multiplicateur avec des bits d'opérandes jusqu'à 35 et 25 bits basés sur DSP48E1,
  • mlt52x25_dsp48e1 - un multiplicateur avec des bits d'opérandes jusqu'à 52 et 25 bits basés sur DSP48E1,
  • mlt44x18_dsp48e2 - multiplicateur avec des bits d'opérandes jusqu'à 44 et 18 bits basés sur DSP48E2,
  • mlt61x18_dsp48e2 - multiplicateur avec bits d'opérande jusqu'à 61 et 18 bits basé sur DSP48E2,
  • mlt35x27_dsp48e2 - multiplicateur avec des bits d'opérande jusqu'à 35 et 27 bits basés sur DSP48E2,
  • mlt52x27_dsp48e2 est un multiplicateur avec des bits d'opérande jusqu'à 52 et 27 bits basés sur DSP48E2.
• Totalisateur:
  
  
  • int_addsub_dsp48 - additionneur universel, bits d'opérande jusqu'à 96 bits.
• Lignes de retard:
  
  
  • int_delay_line - la ligne de base du retard, fournit une permutation des données entre les papillons,
  • int_align_fft - alignement des données d'entrée et des facteurs de retournement à l'entrée du papillon FFT,
  • int_align_fft - alignement des données d'entrée et des facteurs de retournement à l'entrée du papillon OBPF ,
• Facteurs tournants:
  
  
  • rom_twiddle_int - un générateur de facteurs rotatifs, à partir d'une certaine longueur la FFT considère des coefficients basés sur des cellules FPGA DSP,
  • row_twiddle_tay - générateur de facteurs rotatifs utilisant une série de Taylor (NFFT> 2K) **.
• Tampon de données:
  
  
  • inbuf_half_path - tampon d'entrée, reçoit le flux en mode normal et produit deux séquences d'échantillons décalées de la moitié de la longueur de la FFT ***,
  • outbuf_half_path - le tampon de sortie, collecte deux séquences et produit une continue égale à la longueur de la FFT,
  • iobuf_flow_int2 - le tampon fonctionne en deux modes: il reçoit un flux en mode Interleave-2 et produit deux séquences de FFT décalées de moitié. Ou vice versa, selon l'option BITREV.
  • int_bitrev_ord est un simple convertisseur de données de l'ordre naturel au bit-reverse.

* - pour DSP48E1: 25 bits, pour DSP48E2 - 27 bits.
** - à partir d'un certain stade de la FFT, une quantité fixe de mémoire de bloc peut être utilisée pour stocker des coefficients de rotation, et des coefficients intermédiaires peuvent être calculés en utilisant des nœuds DSP48 en utilisant la formule de Taylor à la première dérivée. En raison du fait que la ressource mémoire est plus importante pour la FFT, vous pouvez sacrifier en toute sécurité les unités de calcul pour la mémoire.
*** - tampon d'entrée et lignes à retard - contribuent de manière significative à la quantité de ressources mémoire FPGA occupées

Papillon

Quiconque a rencontré au moins une fois l'algorithme de transformée de Fourier rapide sait que cet algorithme est basé sur une opération élémentaire - un «papillon». Il convertit le flux d'entrée en multipliant l'entrée par le facteur de torsion. Il existe deux schémas de conversion classiques pour les FFT: la décimation en fréquence (DIF, décimation en fréquence) et la décimation en temps (DIT, décimation en temps). L'algorithme DIT est caractérisé en divisant la séquence d'entrée en deux séquences de demi-durée et l'algorithme DIF en deux séquences d'échantillons pairs et impairs de durée NFFT. De plus, ces algorithmes diffèrent dans les opérations mathématiques pour l'opération papillon.



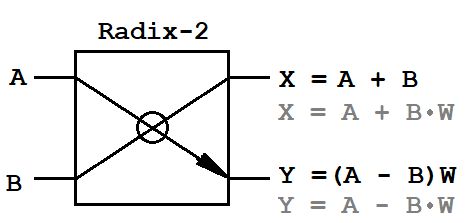A, B - paires d'entrée d'échantillons complexes,
X, Y - paires de sortie d'échantillons complexes,
W - facteurs de retournement complexes.

Les données d'entrée étant des quantités complexes, le papillon nécessite un multiplicateur complexe (4 opérations de multiplication et 2 opérations d'addition) et deux additionneurs complexes (4 opérations d'addition). C'est toute la base mathématique qui doit être implémentée sur le FPGA.

Multiplicateur

Il convient de noter que toutes les opérations mathématiques sur les FPGA sont souvent effectuées dans du code supplémentaire (complément à 2). Le multiplicateur FPGA peut être implémenté de deux manières - sur la logique à l'aide de déclencheurs et de tables LUT, ou sur des unités de calcul DSP48 spéciales, qui ont longtemps et fermement été incluses dans tous les FPGA modernes. Sur les blocs logiques, la multiplication est mise en œuvre à l'aide de l'algorithme de Booth ou de ses modifications, occupe une quantité décente de ressources logiques et ne satisfait pas toujours les contraintes de temps à des fréquences de traitement de données élevées. À cet égard, les multiplicateurs FPGA dans les projets modernes sont presque toujours conçus sur la base de nœuds DSP48 et seulement occasionnellement sur la logique. Un nœud DSP48 est une cellule finie complexe qui implémente des fonctions mathématiques et logiques. Opérations de base: multiplication, addition, soustraction, accumulation, compteur, opérations logiques (XOR, NAND, AND, OR, NOR), quadrature, comparaison de nombres, décalage, etc. La figure suivante montre la cellule DSP48E2 pour la famille Xilinx Ultrascale + FPGA.



Au moyen d'une configuration simple des ports d'entrée, des opérations de calcul dans les nœuds et de la définition des retards à l'intérieur du nœud, vous pouvez créer une batteuse de données mathématiques à grande vitesse.
Notez que tous les principaux fournisseurs de FPGA dans l'environnement de développement ont des cœurs IP standard et gratuits pour calculer les fonctions mathématiques basées sur le nœud DSP48. Ils vous permettent de calculer des fonctions mathématiques primitives et de définir divers retards à l'entrée et à la sortie du nœud. Pour Xilinx, il s'agit du «multiplicateur» IP-Core (version 12.0, 2018), qui vous permet de configurer le multiplicateur à n'importe quelle profondeur de bits des données d'entrée de 2 à 64 bits. De plus, vous pouvez spécifier comment le multiplicateur est implémenté - sur les ressources logiques ou sur les primitives DSP48 intégrées.

Estimez la quantité de logique que le multiplicateur «mange» avec la profondeur de bits des données d'entrée sur les ports A et B = 64 bits. Si vous utilisez les nœuds DSP48, ils n'en auront besoin que de 16.



La principale limitation des cellules DSP48 est la profondeur de bits des données d'entrée. Le nœud DSP48E1, qui est la cellule de base des séries FPGA Xilinx 6 et 7, la largeur des ports d'entrée pour la multiplication: "A" - 25 bits, "B" - 18 bits, Par conséquent, le résultat de la multiplication est un nombre de 43 bits. Pour les familles Xilinx Ultrascale et Ultrascale + FPGA, le nœud a subi plusieurs modifications, notamment la capacité du premier port augmentée de deux bits: «A» - 27 bits, «B» - 18 - bits. De plus, le nœud lui-même est appelé DSP48E2.

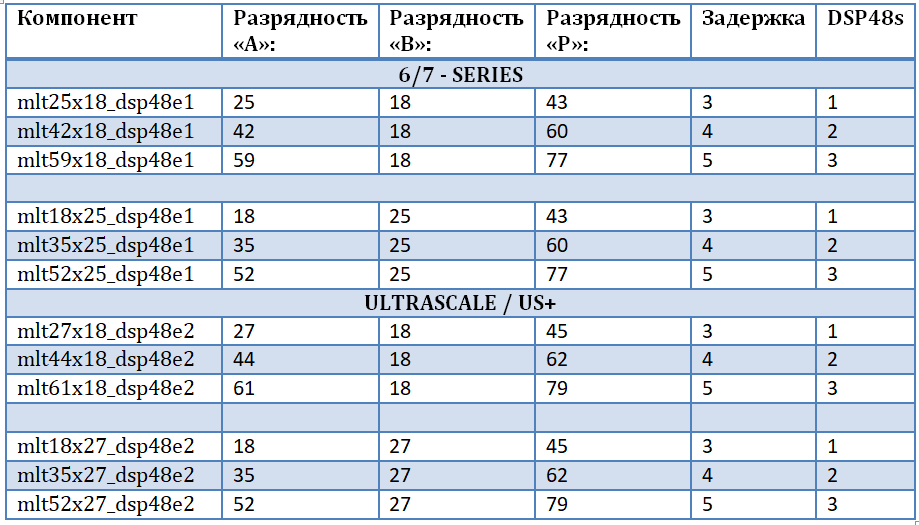
Afin de ne pas être lié à une famille spécifique et à une puce FPGA, pour garantir la «pureté du code source» et pour prendre en compte toutes les profondeurs de bits possibles des données d'entrée, il a été décidé de concevoir notre propre ensemble de multiplicateurs. Cela permettra la mise en œuvre la plus efficace de multiplicateurs complexes pour les papillons FFT, à savoir des multiplicateurs et un additionneur-soustracteur basé sur des blocs DSP48. La première entrée du multiplicateur est les données d'entrée, la deuxième entrée du multiplicateur est les facteurs de rotation (signal harmonique de la mémoire). Un ensemble de multiplicateurs est implémenté à l'aide de la bibliothèque UNISIM intégrée, à partir de laquelle il est nécessaire de connecter les primitives DSP48E1 et DSP48E2 pour leur utilisation ultérieure dans le projet. Un ensemble de multiplicateurs est présenté dans le tableau. Il convient de noter que:

• L'opération de multiplication des nombres entraîne une augmentation de la capacité du produit comme la somme de la capacité des opérandes.
• En fait, chacun des multiplicateurs 25x18 et 27x18 est dupliqué - c'est un composant pour différentes familles.
• Plus la phase de parallélisme de l'opération est grande, plus le délai de calcul est important et plus les ressources occupées sont importantes.
• Avec une profondeur de bits plus faible à l'entrée «B», des multiplicateurs avec une profondeur de bits plus élevée à une autre entrée peuvent être implémentés.
• La principale limitation de l'augmentation de la profondeur de bits est introduite par le port «B» (le port réel de la primitive DSP48) et le registre à décalage interne de 17 bits.

Une nouvelle augmentation de la profondeur de bits n'est pas intéressante dans le cadre de la tâche pour les raisons décrites ci-dessous:

Profondeur de bits des facteurs de rotation

On sait que plus la résolution du signal harmonique est élevée, plus le nombre apparaît avec précision (plus il y a de signes dans la partie fractionnaire). Mais la taille des bits du port est B <25 bits en raison du fait que pour les facteurs de rotation dans les nœuds FFT, cette profondeur de bits est suffisante pour assurer une multiplication de haute qualité du flux d'entrée avec des éléments de signal harmoniques dans les «papillons» (pour toutes les longueurs FFT réalisables sur les FPGA modernes). La valeur typique de la profondeur de bits des coefficients de rotation dans les tâches que j'implémente est de 16 bits, 24 - moins souvent, 32 - jamais.

Profondeur de bits des échantillons d'entrée

La capacité de ces nœuds de réception et d'enregistrement typiques (ADC, DAC) n'est pas grande - de 8 à 16 bits, et rarement - de 24 ou 32 bits. De plus, dans ce dernier cas, il est plus efficace d'utiliser le format de données à virgule flottante selon la norme IEEE-754. D'un autre côté, chaque étape du «papillon» dans la FFT ajoute un bit de données aux échantillons de sortie en raison d'opérations mathématiques. Par exemple, pour une longueur de NFFT = 1024, log2 (NFFT) = 10 papillons est utilisé.

Par conséquent, la profondeur de bits de sortie sera supérieure de dix bits à l'entrée, WOUT = WIN + 10. En général, la formule ressemble à ceci:

WOUT = WIN + log2 (NFFT);

Un exemple:

Profondeur de bits du flux d'entrée WIN = 32 bits,
Profondeur de bits des facteurs de rotation TWD = 27,
La capacité du port «A» de la liste des multiplicateurs mis en œuvre dans cet article ne dépasse pas 52 bits. Cela signifie que le nombre maximum de papillons est FFT = 52-32 = 20. Autrement dit, il est possible de réaliser FFT avec une longueur allant jusqu'à 2 ^ 20 = 1M d'échantillons. (Cependant, dans la pratique, cela n'est pas possible par des moyens directs en raison de ressources limitées, même pour les cristaux FPGA les plus puissants, mais cela se rapporte à un autre sujet et ne sera pas examiné dans l'article).

Comme vous pouvez le voir, c'est l'une des principales raisons pour lesquelles je n'ai pas implémenté de multiplicateurs avec une profondeur de bits plus élevée des ports d'entrée. Les multiplicateurs utilisés couvrent la gamme complète des tailles de bits d' entrée et des facteurs de rotation requis pour le calcul de la FFT entière. Dans tous les autres cas, vous pouvez utiliser le calcul FFT au format virgule flottante !

La mise en place du multiplicateur "large"

Sur la base d'un exemple simple de multiplication de deux nombres qui ne correspondent pas à la profondeur de bits d'un nœud DSP48 standard, je vais montrer comment vous pouvez implémenter un multiplicateur de données large. La figure suivante montre son schéma de principe. Le multiplicateur implémente la multiplication de deux nombres signés dans le code supplémentaire, la largeur du premier opérande X est de 42 bits, le second Y est de 18 bits. Il contient deux nœuds DSP48E2. Deux registres sont utilisés pour égaliser les retards dans le nœud supérieur. Cela est dû au fait que dans l'additionneur supérieur, vous devez ajouter correctement les numéros des nœuds supérieur et inférieur du DSP48. L'additionneur inférieur n'est pas réellement utilisé. À la sortie du nœud inférieur, il y a un retard supplémentaire du produit pour aligner le numéro de sortie avec le temps. Le retard total est de 4 cycles.



Le travail comprend deux volets:

• La partie la plus jeune: P1 = '0' & X [16: 0] * Y [17: 0];
• La partie la plus ancienne: P2 = X [42:17] * Y [17: 0] + (P1 >> 17);

Totalisateur

Comme un multiplicateur, un additionneur peut être construit sur des ressources logiques à l'aide d'une chaîne de transfert ou sur des blocs DSP48. Pour atteindre un débit maximal, une deuxième méthode est préférable. Une primitive DSP48 permet d'implémenter l'opération d'addition jusqu'à 48 bits, deux nœuds jusqu'à 96 bits. Pour la tâche actuelle, de telles profondeurs de bits sont tout à fait suffisantes. De plus, la primitive DSP48 dispose d'un mode spécial «MODE SIMD», qui met en parallèle l'ALU 48 bits intégré en plusieurs opérations avec différentes données de petite capacité. C'est-à-dire que dans le mode "UN" une grille de bits complète de 48 bits et deux opérandes sont utilisés, et dans le mode "DEUX" la grille de bits est divisée en plusieurs flux parallèles de 24 bits chacun (4 opérandes). Ce mode, utilisant un seul additionneur, permet de réduire la quantité de ressources de puces FPGA occupées à de faibles profondeurs de bits d'échantillons d'entrée (lors des premières étapes de calcul).

Augmentation de la profondeur de bits

L'opération de multiplication de deux nombres par les bits N et M dans un code binaire supplémentaire conduit à une augmentation de la capacité des bits de sortie à P = N + M.

Exemple: pour multiplier des nombres à trois bits N = M = 3, le nombre positif maximum est +3 = (011) ₂ et le nombre négatif maximum est 4 = (100) ₂ . Le bit le plus significatif est responsable du signe du nombre. Par conséquent, le nombre maximum possible lors de la multiplication est +16 = (010000) ₂ , qui résulte de la multiplication de deux nombres négatifs maximum -4. La profondeur de bits de la sortie est égale à la somme des bits d'entrée P = N + M = 6 bits.

L'opération consistant à ajouter deux nombres avec les bits N et M dans le code binaire supplémentaire entraîne une augmentation du bit de sortie d'un bit.

Exemple: ajoutez deux nombres positifs, N = M = 3, le nombre positif maximum est 3 = (011) ₂ et le nombre négatif maximum est 4 = (100) ₂ .Le bit le plus significatif est responsable du signe du nombre. Par conséquent, le nombre positif maximum est 6 = (0110) ₂ et le nombre négatif maximum est -8 = (1000) ₂ . La résolution de la sortie augmente d'un bit.

Prise en compte des fonctionnalités de l'algorithme

Troncature de la profondeur de bits par le haut:
pour minimiser les ressources FPGA dans l'algorithme FFT, il a été décidé que lors de la multiplication des données dans un papillon, n'utilisez jamais le nombre négatif maximum possible pour les coefficients de rotation. Cet amendement n'a pas d'incidence négative sur le résultat. Par exemple, lorsque vous utilisez la représentation 16 bits des facteurs de rotation, le nombre minimum est -32768 = 0x8000 et le suivant -32767 = 0x8001. L'erreur lors du remplacement du nombre négatif maximum par la valeur voisine la plus proche sera de ~ 0,003% et est tout à fait acceptable pour la tâche.

En supprimant le nombre minimum dans le produit de deux nombres, à chaque itération, vous pouvez réduire un bit d'ordre élevé inutilisé. Exemple: données - 4 = (100) ₂ , coefficient +3 = (011) ₂. Résultat de multiplication = -12 = (110100) ₂ . Le cinquième bit peut être ignoré car il duplique le voisin, le quatrième est un bit de signe.

Troncature de bits par le bas:

Évidemment, en multipliant le signal d'entrée dans le «papillon» par l'effet harmonique, il n'est pas nécessaire de tirer la profondeur de bits de sortie dans les papillons suivants, mais un arrondi ou une troncature est requis. Les facteurs de rotation sont présentés dans un format M bits pratique, mais en réalité il s'agit d'un sinus et cosinus normal normalisé à l'unité. Autrement dit, le nombre 0x8000 = -1 et le nombre 0x7FFF = +1. Par conséquent, le résultat de la multiplication est nécessairement tronqué à la profondeur de bits d'origine des données (c'est-à-dire que M bits des facteurs de rotation sont tronqués à partir du bas). Dans toutes les implémentations FFT que j'ai vues, les facteurs de retournement sont normalisés à 1 d'une manière ou d'une autre. Par conséquent, à partir du résultat de la multiplication, il est nécessaire de prendre les bits dans la grille suivante [N + M-1-1: M-1]. Le bit le plus significatif n'est pas utilisé (soustrayez le 1 supplémentaire), les moins significatifs sont tronqués.

L'addition / soustraction de données dans les opérations du «papillon» n'est en aucun cas minimisée, et seule cette opération contribue à l' augmentation de la profondeur de bits des données de sortie d'un bit à chaque étape du calcul .

Notez qu'au premier stade de l'algorithme FFT DIT ou au dernier stade de l'algorithme FFT DIF, les données doivent être multipliées par un facteur de rotation avec un indice zéro W0 = {Re, Im} = {1, 0}. Du fait que la multiplication par l'unité et zéro sont des opérations primitives, elles peuvent être omises. Dans ce cas, l'opération de multiplication complexe n'est pas du tout nécessaire: les composants réels et imaginaires subissent un «tour» sans changements. Au deuxième stade, deux coefficients sont utilisés: W0 = {Re, Im} = {1, 0} et W1 = {Re, Im} = {0, -1}. De même, les opérations peuvent être réduites à des transformations élémentaires et utiliser un multiplexeur pour sélectionner l'échantillon de sortie. Cela vous permet de sauvegarder de manière significative les blocs DSP48 sur les deux premiers papillons.

Le multiplicateur complexe est construit de la même manière - sur la base des multiplicateurs et de l'additionneur-soustracteur, cependant, pour certaines options pour la profondeur de bits des données d'entrée, aucune ressource supplémentaire n'est requise, ce qui sera décrit ci-dessous.

Le tampon d'entrée et les lignes à retard et les commutateurs croisés sont similaires à ceux décrits dans l'article précédent. Les facteurs de rotation deviennent des entiers avec une profondeur de bits configurable. Sinon, il n'y a aucun changement global dans la conception du cœur FFT.

Fonctions de base de la FFT INT_FFTK

• Schéma de traitement des données entièrement canalisé.
• Longueur de conversion NFFT = 8-512K points.
• Réglage flexible de la longueur de conversion NFFT.
• Format d'entrée entier, la largeur de bit est configurable.
• Format entier des facteurs rotatifs, la largeur de bit est configurable.
• .
• !
• .
• : – , -.
• : - , – .
• . Radix-2.
• NFFT *.
• .
• (Virtex-6, 7-Series, Ultrascale).
• ~375MHz Kintex-7
• – VHDL.
• bitreverse +.
• Projet open source sans inclusion de cœurs IP tiers.

Code source

Le code source du noyau FFT INTFFTK sur VHDL (y compris les opérations de base et un ensemble de multiplicateurs) et les scripts m pour Matlab / Octave sont disponibles dans mon profil sur le github .

Conclusion

Au cours du développement, un nouveau cœur FFT a été conçu, qui offre de meilleures performances par rapport aux pairs. La combinaison des cœurs FFT et OBPF ne nécessite pas de traduction en ordre naturel, et la longueur de conversion maximale n'est limitée que par les ressources FPGA. La double concurrence vous permet de traiter des flux d'entrée double fréquence, ce que IP-CORE Xilinx ne peut pas faire. La profondeur de bits à la sortie de la FFT entière augmente linéairement en fonction du nombre d'étages de conversion.

Dans un article précédent, j'ai écrit sur les plans futurs: FFT core Radix-4, Radix-8, Ultra-Long FFT pour plusieurs millions de points, FFT-FP32 (au format IEEE-754). Bref, presque tous sont autorisés, mais pour une raison ou une autre, ils ne peuvent pas être rendus publics pour le moment. L'exception est l'algorithme FFT Radix-8, avec lequel je n'ai même pas pris la peine (difficile et paresseux).

Encore une fois, j'exprime ma gratitude à dsmv2014 , qui a toujours accueilli mes idées aventureuses. Merci de votre attention!

MISE À JOUR 2018/08/22

Ajout de l'option SCALED FFT / IFFT aux codes source . Sur chaque papillon, la profondeur de bits est tronquée de 1 bit (tronquer LSB). Profondeur de bits de sortie = profondeur de bits d'entrée.

De plus, je donnerai deux graphiques du passage d'un signal réel à travers le FPGA pour montrer la propriété intégrale de la transformation, c'est-à-dire: comment la troncature affecte le résultat de l'accumulation d'erreurs à la sortie FFT. Il est connu de la théorie qu'en raison de la transformée de Fourier, le rapport signal / bruit se détériore lorsque le signal d'entrée est tronqué par rapport à la version non tronquée.

Exemple: L'amplitude de l'amplitude d'entrée est de 6 bits. Le signal est une onde sinusoïdale à 128 échantillons PF. NFFT = 1024 échantillons, DATA_WIDTH = 16, TWDL_WIDTH = 16.

Comme vous pouvez le voir, l'option SCALED n'a pas «tiré» l'onde sinusoïdale du bruit, tandis que l'option UNSCALED a montré un bon résultat.