Présentation de l'algorithme d'entretien d'embauche - Génération de jeu

Bonjour, Habr!

Ce poste commence l'analyse des tâches selon les algorithmes que les grandes entreprises informatiques (Mail.Ru Group, Google, etc.) aiment donner aux candidats pour les entretiens (si l'entretien avec les algorithmes n'est pas bon, alors les chances de trouver un emploi dans une entreprise de rêve, hélas tendent à zéro). Tout d'abord, ce poste est utile pour ceux qui n'ont pas l'expérience de la programmation d'olympiades ou de cours lourds comme ShAD ou LKS, dans lesquels les sujets des algorithmes sont pris suffisamment au sérieux, ou pour ceux qui veulent rafraîchir leurs connaissances dans un certain domaine.

Dans le même temps, on ne peut pas affirmer que toutes les tâches qui seront traitées ici seront certainement remplies lors de l'entretien, cependant, les approches par lesquelles ces tâches sont résolues sont similaires dans la plupart des cas.

La narration sera divisée en différents sujets, et nous commencerons par générer des ensembles avec une structure spécifique.

1. Commençons par l'accordéon de bouton: vous devez générer toutes les séquences de crochets correctes avec des crochets du même type ( quelle est la séquence de crochets correcte ), où le nombre de crochets est k.

Ce problème peut être résolu de plusieurs manières. Commençons par récursif .

Cette méthode suppose que nous commençons à parcourir les séquences d'une liste vide. Une fois la parenthèse (ouverture ou fermeture) ajoutée à la liste, l'appel de récursivité est à nouveau effectué et les conditions sont vérifiées. Quelles sont les conditions? Il est nécessaire de surveiller la différence entre les parenthèses ouvrantes et fermantes (variable cnt ) - vous ne pouvez pas ajouter une parenthèse fermante à la liste si cette différence n'est pas positive, sinon la séquence des parenthèses cessera d'être correcte. Il reste à implémenter soigneusement cela dans le code.

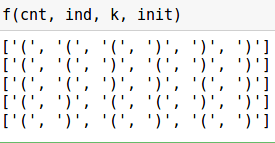
 k = 6 #   init = list(np.zeros(k)) #  ,    cnt = 0 #    ind = 0 # ,       def f(cnt, ind, k, init): #  . ,     if (cnt <= k-ind-2): init[ind] = '(' f(cnt+1, ind+1, k, init) # .    ,  cnt > 0 if cnt > 0: init[ind] = ')' f(cnt-1, ind+1, k, init) #      if ind == k: if cnt == 0: print (init) 

La complexité de cet algorithme est $$$O ((C_k ^ {k / 2} - C_k ^ {k / 2 -1}) * k)$mémoire supplémentaire requise $$$O (k)$.

Avec les paramètres donnés, l'appel de fonction $$$f (cnt, ind, k, init)$affichera les éléments suivants:

Une manière itérative de résoudre ce problème: dans ce cas, l'idée sera fondamentalement différente - vous devez introduire le concept d'ordre lexicographique pour les séquences de parenthèses.

Toutes les séquences de parenthèses correctes pour un type de parenthèse peuvent être commandées en tenant compte du fait que $$$'(' <')'$. Par exemple, pour n = 6, la séquence la plus lexicographiquement inférieure est $$$((()))$et le plus ancien - $$$() () ()$.

Pour obtenir la séquence lexicographique suivante, vous devez trouver la parenthèse ouvrante la plus à droite, devant laquelle il y a une parenthèse fermante, de sorte que lorsqu'ils sont échangés par endroits, la séquence de parenthèses reste correcte. Nous les échangeons et faisons du suffixe le mineur lexicographique - pour cela, vous devez calculer à chaque étape la différence entre le nombre de parenthèses.

À mon avis, cette approche est un peu morne que récursive, mais elle peut être utilisée pour résoudre d'autres problèmes de groupes électrogènes. Nous implémentons cela dans le code.

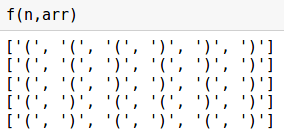
 #  ,    n = 6 arr = ['(' for _ in range(n//2)] + [')' for _ in range(n//2)] def f(n, arr): #    print (arr) while True: ind = n-1 cnt = 0 #  . ,    while ind>=0: if arr[ind] == ')': cnt -= 1 if arr[ind] == '(': cnt += 1 if cnt < 0 and arr[ind] =='(': break ind -= 1 #   ,     if ind < 0: break #   .  arr[ind] = ')' #      for i in range(ind+1,n): if i <= (n-ind+cnt)/2 +ind: arr[i] = '(' else: arr[i] = ')' print (arr) 

La complexité de cet algorithme est la même que dans l'exemple précédent.

Soit dit en passant, il existe une méthode simple qui démontre que le nombre de séquences de parenthèses générées pour un n / 2 donné doit correspondre aux nombres catalans .

Ça marche!

Très bien, avec les crochets pour l'instant, passons à la génération de sous-ensembles. Commençons par un puzzle simple.

2. Étant donné un tableau d'ordre croissant avec des nombres de $$$0$avant $$$n-1$, il est nécessaire de générer tous ses sous-ensembles.

Notez que le nombre de sous-ensembles d'un tel ensemble est exactement $$$2 ^ n$. Si chaque sous-ensemble est représenté comme un tableau d'indices, où $$$0$signifie que l'élément n'est pas inclus dans l'ensemble, mais $$$1$- ce qui est inclus, alors la génération de tous ces tableaux sera la génération de tous les sous-ensembles.

Si nous considérons la représentation binaire des nombres de 0 à $$ , puis ils spécifieront les sous-ensembles souhaités. Autrement dit, pour résoudre le problème, il est nécessaire de mettre en œuvre l'addition de l'unité à un nombre binaire. Nous commençons par tous les zéros et finissons par un tableau dans lequel il y a une unité.

 n = 3 B = np.zeros(n+1) #  B   1  (    ) a = np.array(list(range(n))) #   def f(B, n, a): #   while B[0] == 0: ind = n #     while B[ind] == 1: ind -= 1 #   1 B[ind] = 1 #      B[(ind+1):] = 0 print (a[B[1:].astype('bool')]) 

La complexité de cet algorithme est $$$O (n * 2 ^ n)$, de mémoire - $$$O (n)$.

Maintenant, compliquons un peu la tâche précédente.

3. Étant donné un tableau ordonné dans l'ordre croissant avec des nombres de $$$0$avant $$$n-1$, vous devez tout générer $$$k$- sous-ensembles d'éléments (résolus de manière itérative).

Je note que la formulation de ce problème est similaire à la précédente et qu'il peut être résolu en utilisant approximativement la même méthodologie: prenez le tableau initial avec $$$k$unités et $$$n-k$zéros et trier séquentiellement toutes les variantes de ces séquences de longueur $$$n.$

Cependant, des modifications mineures sont nécessaires. Nous devons tout trier $$$k$-des ensembles de nombres évalués $$$0$avant $$$n-1$. Vous devez comprendre exactement comment vous devez trier les sous-ensembles. Dans ce cas, nous pouvons introduire le concept d'ordre lexicographique pour de tels ensembles.

Nous organisons également la séquence par codes de caractères: $$$1 <0$(Bien sûr, c'est étrange, mais c'est nécessaire, et maintenant nous comprendrons pourquoi). Par exemple, pour $$$n = 4, k = 2$le plus jeune et le plus âgé sera la séquence $$ et $$$[0,0,1,1]$.

Reste à comprendre comment décrire la transition d'une séquence à une autre. Ici, tout est simple: si on change $$$1$sur $$$0$, puis à gauche nous écrivons le lexicographiquement minimal en tenant compte de la préservation du $$$k$. Code:

 n = 5 k = 3 a = np.array(list(range(n))) #    k -   init = [1 for _ in range(k)] + [0 for _ in range(nk)] def f(a, n, k, init): #   k-  print (a[a[init].astype('bool')]) while True: unit_cnt = 0 cur_ind = 0 #   ,     1 while (cur_ind < n) and (init[cur_ind]==1 or unit_cnt==0): if init[cur_ind] == 1: unit_cnt += 1 cur_ind += 1 #        -    if cur_ind == n: break #  init[cur_ind] = 1 #   . .  for i in range(cur_ind): if i < unit_cnt-1: init[i] = 1 else: init[i] = 0 print (a[a[init].astype('bool')]) 

Exemple de travail:

La complexité de cet algorithme est $$$O (C_n ^ k * n)$, de mémoire - $$$O (n)$.

4. Étant donné un tableau d'ordre croissant avec des nombres de $$$0$avant $$$n-1$, vous devez tout générer $$$k$-élément sous-ensembles (résoudre récursivement).

Essayons maintenant la récursivité. L'idée est simple: cette fois sans description, voir le code.

 n = 5 a = np.array(list(range(n))) ind = 0 # ,       num = 0 # ,       k = 3 sub = list(-np.ones(k)) #  def f(n, a, num, ind, k, sub): #   k  ,     if ind == k: print (sub) else: for i in range(n - num): #  ,      k  if (n - num - i >= k - ind): #      sub[ind] = a[num + i] #     f(n, a, num+1+i, ind+1, k, sub) 

Exemple de travail:

La complexité est la même que dans la méthode précédente.

5. Étant donné un tableau d'ordre croissant avec des nombres de $$$0$avant $$$n-1$, il est nécessaire de générer toutes ses permutations.

Nous allons résoudre en utilisant la récursivité. La solution est similaire à la précédente, où nous avons une liste auxiliaire. Il est initialement nul si allumé $$$i$-le lieu de l'élément est une unité, puis l'élément $$$i$déjà dans la permutation. Aussitôt dit, aussitôt fait:

 a = np.array(range(3)) n = a.shape[0] ind_mark = np.zeros(n) #   perm = -np.ones(n) #     def f(ind_mark, perm, ind, n): if ind == n: print (perm) else: for i in range(n): if not ind_mark[i]: #     ind_mark[i] = 1 #   perm[ind] = i f(ind_mark, perm, ind+1, n) #   -    ind_mark[i] = 0 

Exemple de travail:

La complexité de cet algorithme est $$$O (n ^ 2 * n!)$, de mémoire - $$$O (n).$

Considérons maintenant deux puzzles très intéressants pour les codes Gray . En bref, il s'agit d'un ensemble de séquences de même longueur, où chaque séquence diffère de ses voisines dans une catégorie.

6. Générez tous les codes Gray bidimensionnels de longueur n.

L'idée de résoudre ce problème est cool, mais si vous ne connaissez pas la solution, il peut être très difficile de penser. Je note que le nombre de ces séquences est $$$2 ^ n$.

Nous allons résoudre de manière itérative. Supposons que nous ayons généré une partie de ces séquences et qu'elles se trouvent dans une liste. Si nous dupliquons une telle liste et l'écrivons dans l'ordre inverse, la dernière séquence de la première liste coïncide avec la première séquence de la deuxième liste, l'avant-dernière coïncide avec la seconde, etc. Combinez ces listes en une seule.

Que faut-il faire pour que toutes les séquences de la liste diffèrent les unes des autres dans la même catégorie? Mettez une unité aux endroits appropriés dans les éléments de la deuxième liste pour obtenir les codes Gray.

Il est difficile de percevoir «à l'oreille», nous allons décrire les itérations de cet algorithme.

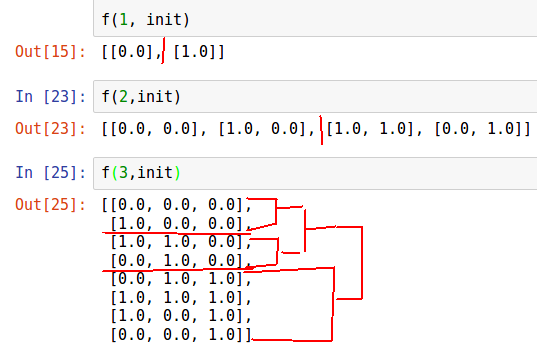
 n = 3 init = [list(np.zeros(n))] def f(n, init): for i in range(n): for j in range(2**i): init.append(list(init[2**i - j - 1])) init[-1][i] = 1.0 return init 

La complexité de cette tâche est $$$O (n * 2 ^ n)$, de mémoire la même chose.

Maintenant, compliquons la tâche.

7. Générez tous les codes Gray de dimension k de longueur n.

Il est clair que la tâche passée n'est qu'un cas particulier de cette tâche. Cependant, de la belle manière dont la tâche passée a été résolue, cela ne peut pas être résolu; ici, il est nécessaire de trier les séquences dans le bon ordre. Obtenons un tableau à deux dimensions $$$k * n$. Initialement, la dernière ligne a des unités et les autres ont des zéros. De plus, dans la matrice, $$$-1$. Ici $$$1$et $$$-1$diffèrent les uns des autres dans le sens: $$$1$pointe vers le haut $$$-1$pointe vers le bas. Important: dans chaque colonne à tout moment il ne peut y en avoir qu'une $$$1$ou $$$-1$et les chiffres restants seront des zéros.

Nous allons maintenant comprendre comment il est possible de trier ces séquences afin d'obtenir des codes Gray. Commencez par la fin pour déplacer l'élément vers le haut.

À l'étape suivante, nous avons atteint le plafond. Nous écrivons la séquence résultante. Après avoir atteint la limite, vous devez commencer à travailler avec la colonne suivante. Vous devez la rechercher de droite à gauche, et si nous trouvons une colonne qui peut être déplacée, alors pour toutes les colonnes avec lesquelles nous ne pouvons pas travailler, les flèches changeront dans la direction opposée afin qu'elles puissent être déplacées à nouveau.

Vous pouvez maintenant déplacer la première colonne vers le bas. Nous le déplaçons jusqu'à ce qu'il touche le sol. Et ainsi de suite, jusqu'à ce que toutes les flèches atteignent le sol ou le plafond et qu'il ne reste plus de colonnes pouvant être déplacées.

Cependant, dans le cadre de l'économie de mémoire, nous allons résoudre ce problème en utilisant deux tableaux unidimensionnels de longueur $$$n$: dans un tableau les éléments de la séquence eux-mêmes se trouveront, et dans l'autre de leur direction (flèches).

 n,k = 3,3 arr = np.zeros(n) direction = np.ones(n) #   ,    def k_dim_gray(n,k): #    print (arr) while True: ind = n-1 while ind >= 0: #    ,    if (arr[ind] == 0 and direction[ind] == 0) or (arr[ind] == k-1 and direction[ind] == 1): direction[ind] = (direction[ind]+1)%2 else: break ind -= 1 #     ,     if ind < 0: break #    1 ,   1  arr[ind] += direction[ind]*2 - 1 print (arr) 

Exemple de travail:

La complexité de l'algorithme est $$$O (n * k ^ n)$, de mémoire - $$$O (n)$.

La justesse de cet algorithme est prouvée par induction sur $$$n$, ici je ne décrirai pas les preuves.

Dans le prochain article, nous analyserons les tâches pour la dynamique.