AI, cours pratique. Le modèle de base pour reconnaître les émotions dans les images

Dans cet article, nous allons construire un modèle de base d'un réseau neuronal convolutif capable de reconnaître les émotions dans les images. La reconnaissance des émotions dans notre cas est une tâche de classification binaire, dont le but est de diviser les images en positives et négatives.

Tous les codes, documents de bloc-notes et autres documents, y compris le Dockerfile, peuvent être trouvés ici .

Les données

La première étape de pratiquement toutes les tâches d'apprentissage automatique consiste à comprendre les données. Faisons-le.

Structure du jeu de données

Les données brutes peuvent être téléchargées ici (dans le document Baseline.ipynb , toutes les actions de cette section sont effectuées automatiquement). Initialement, les données sont dans l'archive au format Zip *. Déballez-le et familiarisez-vous avec la structure des fichiers reçus.



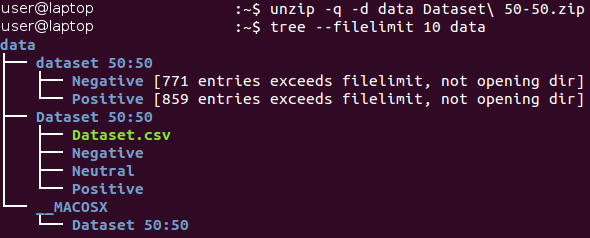
Toutes les images sont stockées dans le catalogue «dataset 50:50» et réparties entre ses deux sous-répertoires, dont le nom correspond à leur classe - Negative et Positive. Veuillez noter que la tâche est un peu déséquilibrée - 53% des images sont positives et seulement 47% sont négatives. En règle générale, les données relatives aux problèmes de classification sont considérées comme déséquilibrées si le nombre d'exemples dans différentes classes varie de manière très significative. Il existe un certain nombre de façons de travailler avec des données non équilibrées - par exemple, suréchantillonnage, suréchantillonnage, modification du poids des données, etc. Dans notre cas, le déséquilibre est insignifiant et ne devrait pas affecter considérablement le processus d'apprentissage. Il suffit de se rappeler que le classificateur naïf, donnant toujours la valeur «positive», fournira une valeur de précision d'environ 53% pour cet ensemble de données.

Regardons quelques images de chaque classe.

Négatif







Positif







À première vue, les images de différentes classes sont en fait différentes les unes des autres. Cependant, faisons une étude plus approfondie et essayons de trouver de mauvais exemples - des images similaires appartenant à différentes classes.

Par exemple, nous avons environ 90 images de serpents étiquetés négatifs et environ 40 images très similaires de serpents étiquetés positifs.

Image positive d'un serpent



Image négative d'un serpent



La même dualité se produit avec les araignées (130 images négatives et 20 images positives), la nudité (15 images négatives et 45 images positives) et certaines autres classes. On a le sentiment que le marquage des images a été effectué par différentes personnes, et leur perception de la même image peut différer. Par conséquent, l'étiquetage contient son incohérence inhérente. Ces deux images de serpents sont presque identiques, tandis que différents experts les ont attribuées à différentes classes. Ainsi, nous pouvons conclure qu'il est à peine possible d'assurer une précision de 100% lorsque vous travaillez avec cette tâche en raison de sa nature. Nous pensons qu'une estimation plus réaliste de la précision serait une valeur de 80% - cette valeur est basée sur la proportion d'images similaires trouvées dans différentes classes lors d'un contrôle visuel préliminaire.

Séparation du processus de formation / vérification

Nous nous efforçons toujours de créer le meilleur modèle possible. Mais quelle est la signification de ce concept? Il existe de nombreux critères différents pour cela, tels que: la qualité, le délai (apprentissage + sortie) et la consommation de mémoire. Certains d'entre eux peuvent être mesurés facilement et objectivement (par exemple, le temps et la taille de la mémoire), tandis que d'autres (la qualité) sont beaucoup plus difficiles à déterminer. Par exemple, votre modèle peut démontrer une précision de 100% lors de l'apprentissage à partir d'exemples qui ont été utilisés à de nombreuses reprises, mais ne fonctionne pas avec de nouveaux exemples. Ce problème est appelé surapprentissage et est l'un des plus importants dans l'apprentissage automatique. Il y a aussi le problème du sous- ajustement : dans ce cas, le modèle ne peut pas apprendre des données présentées et montre de mauvaises prédictions même lors de l'utilisation d'un ensemble de données d'entraînement fixe.

Pour résoudre le problème du sur-ajustement, la technique dite de maintien d'une partie des échantillons est utilisée . Son idée principale est de diviser les données source en deux parties:

• Un ensemble de formation , qui constitue généralement la majeure partie de l'ensemble de données et est utilisé pour former le modèle.
• L'ensemble de test est généralement une petite partie des données source, qui est divisée en deux parties avant d'effectuer toutes les procédures de formation. Cet ensemble n'est pas du tout utilisé en formation et est considéré comme de nouveaux exemples pour tester le modèle après la fin de la formation.

En utilisant cette méthode, nous pouvons observer à quel point notre modèle se généralise (c'est-à-dire qu'il fonctionne avec des exemples inconnus auparavant).

Cet article utilisera un rapport 4/1 pour les ensembles de formation et de test. Une autre technique que nous utilisons est la stratification dite. Ce terme fait référence au partitionnement de chaque classe indépendamment de toutes les autres classes. Cette approche permet de maintenir le même équilibre entre les tailles de classe dans les ensembles de formation et de test. La stratification utilise implicitement l'hypothèse que la distribution des exemples ne change pas lorsque les données source changent et reste la même lors de l'utilisation de nouveaux exemples.



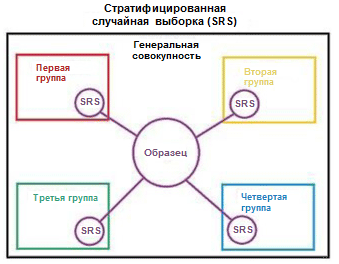
Nous illustrons le concept de stratification avec un exemple simple. Supposons que nous ayons quatre groupes / classes de données contenant un nombre approprié d'objets: enfants (5), adolescents (10), adultes (80) et personnes âgées (5); voir photo à droite (de Wikipedia ). Maintenant, nous devons diviser ces données en deux ensembles d'échantillons dans un rapport de 3/2. Lors de la stratification des exemples, la sélection des objets se fera indépendamment de chaque groupe: 2 objets du groupe d'enfants, 4 objets du groupe d'adolescents, 32 objets du groupe d'adultes et 2 objets du groupe de personnes âgées. Le nouvel ensemble de données contient 40 objets, ce qui correspond exactement aux 2/5 des données d'origine. Dans le même temps, l'équilibre entre les classes du nouvel ensemble de données correspond à leur équilibre dans les données source.

Toutes les actions ci-dessus sont implémentées dans une seule fonction, qui est appelée prepare_data ; cette fonction se trouve dans le fichier Python utils.py . Cette fonction charge les données, les divise en ensembles d'apprentissage et de test à l'aide d'un nombre aléatoire fixe (pour une lecture ultérieure), puis répartit les données en conséquence entre les répertoires du disque dur pour une utilisation ultérieure.

Prétraitement et augmentation

Dans l'un des articles précédents, les actions de prétraitement et les raisons possibles de leur utilisation sous forme d'augmentation des données ont été décrites. Les réseaux de neurones convolutifs sont des modèles assez complexes, et de grandes quantités de données sont nécessaires pour les former. Dans notre cas, il n'y a que 1600 exemples - ce n'est bien sûr pas suffisant.

Par conséquent, nous voulons étendre l'ensemble de données utilisé par l' augmentation des données. Conformément aux informations contenues dans l'article sur le prétraitement des données, la bibliothèque Keras * offre la possibilité d'augmenter les données à la volée lors de leur lecture sur le disque dur. Cela peut être fait via la classe ImageDataGenerator .



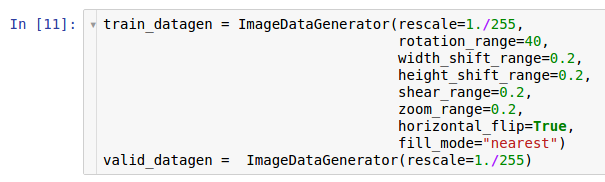
Deux instances des générateurs sont créées ici. La première instance est destinée à la formation et utilise de nombreuses transformations aléatoires - telles que la rotation, le décalage, la convolution, la mise à l'échelle et la rotation horizontale - lors de la lecture des données du disque et de leur transfert vers le modèle. Par conséquent, le modèle reçoit les exemples convertis et chaque exemple reçu par le modèle est unique en raison de la nature aléatoire de cette conversion. La deuxième copie sert à la vérification et ne fait que zoomer sur les images. Les générateurs d'apprentissage et de test n'ont qu'une seule transformation commune: le zoom. Pour assurer la stabilité de calcul du modèle, il est nécessaire d'utiliser la plage [0; 1] au lieu de [0; 255].

Architecture du modèle

Après avoir étudié et préparé les données initiales, l'étape de création du modèle suit. Puisqu'une petite quantité de données est à notre disposition, nous allons construire un modèle relativement simple afin de pouvoir le former de manière appropriée et éliminer la situation de sur-ajustement. Essayons l' architecture de style VGG , mais utilisons moins de couches et de filtres.





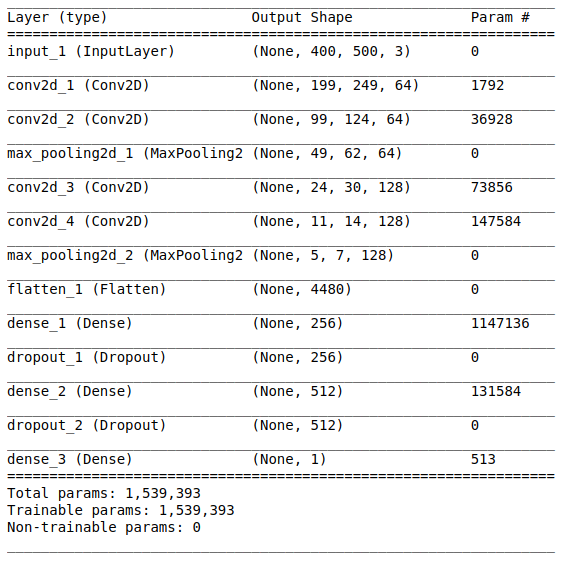
L'architecture du réseau comprend les parties suivantes:
[Couche de convolution + couche de convolution + sélection de la valeur maximale] × 2
La première partie contient deux couches convolutives superposées avec 64 filtres (avec taille 3 et étape 2) et une couche pour sélectionner la valeur maximale (avec taille 2 et étape 2) située après eux. Cette partie est également communément appelée unité d'extraction de caractéristiques , car les filtres extraient efficacement des caractéristiques significatives des données d'entrée (voir l'article Présentation des réseaux de neurones convolutifs pour la classification des images pour plus d'informations).

Alignement

Cette partie est obligatoire, car des tenseurs quadridimensionnels sont obtenus en sortie de la partie convolutionnelle (exemples, hauteur, largeur et canaux). Cependant, pour une couche ordinaire entièrement connectée, nous avons besoin d'un tenseur bidimensionnel (exemples, caractéristiques) en entrée. Par conséquent, il est nécessaire d' aligner le tenseur autour des trois derniers axes afin de les combiner en un seul axe. En fait, cela signifie que nous considérons chaque point de chaque carte d'entités comme une propriété distincte et les alignons en un seul vecteur. La figure ci-dessous montre un exemple d'une image 4 × 4 avec 128 canaux, qui est alignée dans un vecteur étendu avec une longueur de 1024 éléments.



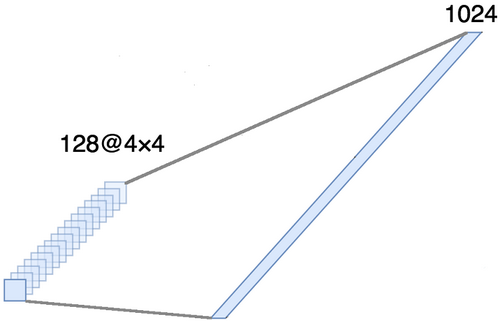[Couche complète + méthode d'exclusion] × 2

Voici la partie classification du réseau. Elle prend une vue alignée des caractéristiques des images et essaie de les classer de la meilleure façon possible. Cette partie du réseau est constituée de deux blocs superposés constitués d'une couche entièrement connectée et d' une méthode d'exclusion . Nous avons déjà fait la connaissance de couches entièrement connectées - il s'agit généralement de couches avec une connexion entièrement connectée. Mais qu'est-ce que la «méthode d'exclusion»? La méthode d'exclusion est une technique de régularisation qui permet d'éviter le sur-ajustement. Un des signes possibles de sur-ajustement est des valeurs extrêmement différentes des coefficients de poids (ordres de grandeur). Il existe de nombreuses façons de résoudre ce problème, notamment la réduction de poids et la méthode d'élimination. L'idée de la méthode d'élimination est de déconnecter les neurones aléatoires pendant l'entraînement (la liste des neurones déconnectés doit être mise à jour après chaque package / ère de formation). Cela empêche très fortement d'obtenir des valeurs complètement différentes pour les coefficients de pondération - de cette façon, le réseau est régularisé.



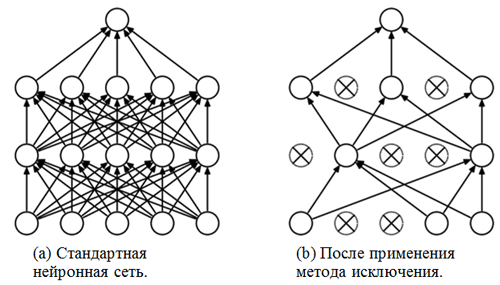
Un exemple de l'application de la méthode d'exclusion (la figure est tirée de l'article Méthode d'exclusion: un moyen facile de prévenir le sur-ajustement dans les réseaux de neurones ):

Module sigmoïde

La couche de sortie doit correspondre à l'énoncé du problème. Dans ce cas, nous traitons du problème de classification binaire, par conséquent, nous avons besoin d'un neurone de sortie avec une fonction d'activation sigmoïde , qui estime la probabilité P d'appartenir à la classe avec le numéro 1 (dans notre cas, ce seront des images positives). Ensuite, la probabilité d'appartenir à la classe avec le numéro 0 (images négatives) peut facilement être calculée comme 1 - P.

Paramètres et options de formation

Nous avons choisi l'architecture du modèle et l'avons spécifiée à l'aide de la bibliothèque Keras pour le langage Python. De plus, avant de commencer la formation du modèle, il est nécessaire de la compiler .



Au stade de la compilation, le modèle est réglé pour la formation. Dans ce cas, trois paramètres principaux doivent être spécifiés:

• L'optimiseur . Dans ce cas, nous utilisons l'optimiseur par défaut Adam *, qui est un type d'algorithme de descente de gradient stochastique avec un moment et une vitesse d'apprentissage adaptative (pour plus d'informations, voir l'entrée de blog de S.Ruder Présentation des algorithmes d'optimisation de la descente de gradient ).
• Fonction de perte . Notre tâche est un problème de classification binaire, il serait donc approprié d'utiliser l' entropie croisée binaire comme fonction de perte.
• Mesures . Il s'agit d'un argument facultatif avec lequel vous pouvez spécifier des mesures supplémentaires à suivre pendant le processus de formation. Dans ce cas, nous devons suivre la précision avec la fonction objectif.

Nous sommes maintenant prêts à former le modèle. Veuillez noter que la procédure de formation est effectuée à l'aide des générateurs initialisés dans la section précédente.

Le nombre d'époques est un autre hyperparamètre qui peut être personnalisé. Ici, nous lui attribuons simplement une valeur de 10. Nous voulons également enregistrer le modèle et l'historique d'apprentissage afin de pouvoir le télécharger plus tard.

Évaluation

Voyons maintenant à quel point notre modèle fonctionne. Tout d'abord, nous considérons le changement de métriques dans le processus d'apprentissage.



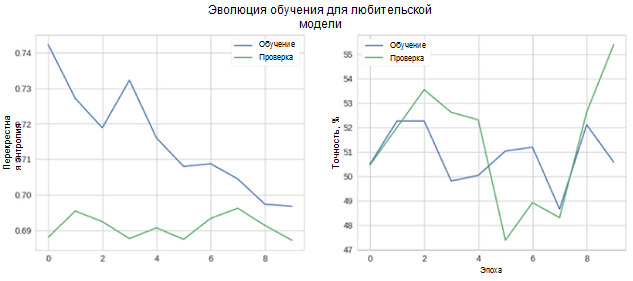
Sur la figure, vous pouvez voir que l'entropie croisée de la vérification et de la précision ne diminue pas avec le temps. De plus, la métrique de précision pour l'ensemble d'apprentissage et de test fluctue simplement autour de la valeur d'un classificateur aléatoire. La précision finale de l'ensemble de test est de 55%, ce qui n'est que légèrement meilleur qu'une estimation aléatoire.

Voyons comment les prédictions du modèle sont réparties entre les classes. Pour cela, il est nécessaire de créer et de visualiser une matrice d'inexactitudes à l'aide de la fonction correspondante du package Sklearn * pour le langage Python.
Chaque cellule de la matrice des inexactitudes a son propre nom:

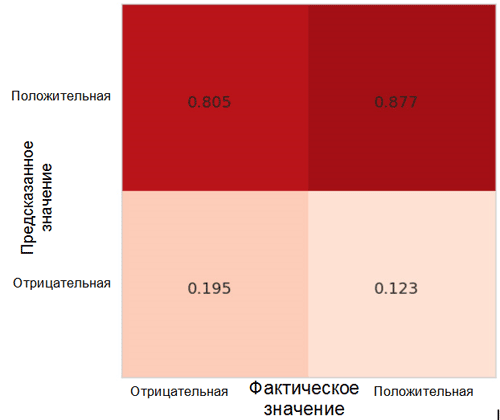
• True Positive Rate = TPR (cellule supérieure droite) représente la proportion d'exemples positifs (classe 1, c'est-à-dire les émotions positives dans notre cas), correctement classés comme positifs.
• Taux de faux positifs = FPR (cellule inférieure droite) représente la proportion d'exemples positifs qui sont incorrectement classés comme négatifs (classe 0, c'est-à-dire les émotions négatives).
• True Negative Rate = TNR (cellule inférieure gauche) représente la proportion d'exemples négatifs correctement classés comme négatifs.
• Taux de faux négatifs = FNR (cellule supérieure gauche) représente la proportion d'exemples négatifs qui sont incorrectement classés comme positifs.

Dans notre cas, le TPR et le FPR sont proches de 1. Cela signifie que presque tous les objets ont été classés comme positifs. Ainsi, notre modèle n'est pas très éloigné du modèle de base naïf avec des prédictions constantes d'une classe plus large (dans notre cas, ce sont des images positives).

Une autre métrique intéressante qui est intéressante à observer est la courbe de performance du récepteur (courbe ROC) et la zone sous cette courbe (ROC AUC). Une définition formelle de ces concepts peut être trouvée ici . En un mot, la courbe ROC montre à quel point le classificateur binaire fonctionne.

Le classificateur de notre réseau neuronal convolutif a un module sigmoïde en sortie, qui attribue la probabilité de l'exemple à la classe 1. Supposons maintenant que notre classificateur montre du bon travail et attribue des valeurs de faible probabilité pour les exemples de classe 0 (l'histogramme vert dans la figure ci-dessous) des valeurs de probabilité élevées pour les exemples Classe 1 (histogramme bleu).



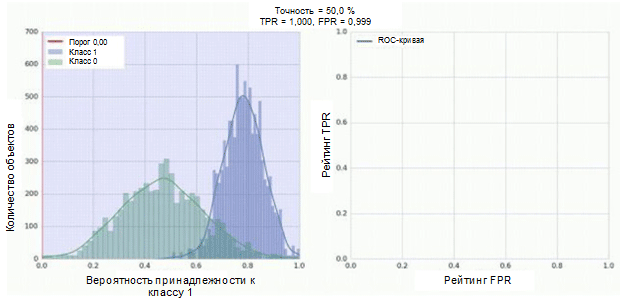
La courbe ROC montre comment l'indicateur TPR dépend de l'indicateur FPR lors du déplacement du seuil de classification de 0 à 1 (figure de droite, partie supérieure). Pour une meilleure compréhension du concept de seuil, rappelez-vous que nous avons la probabilité d'appartenir à la classe 1 pour chaque exemple. Cependant, la probabilité n'est pas encore une étiquette de classe. Par conséquent, il doit être comparé à un seuil pour déterminer à quelle classe l'exemple appartient. Par exemple, si la valeur seuil est 1, tous les exemples doivent être classés comme appartenant à la classe 0, car la valeur de probabilité ne peut pas être supérieure à 1, tandis que les valeurs des indicateurs FPR et TPR seront égales à 0 (car aucun des échantillons n'est classé comme positif ) Cette situation correspond au point le plus à gauche de la courbe ROC. De l'autre côté de la courbe, il y a un point où la valeur de seuil est 0: cela signifie que tous les échantillons sont classés comme appartenant à la classe 1, et les valeurs de TPR et de FPR sont égales à 1. Les points intermédiaires montrent le comportement de la dépendance TPR / FPR lorsque la valeur de seuil change.

La ligne diagonale sur le graphique correspond à un classificateur aléatoire. Mieux notre classificateur fonctionne, plus sa courbe est proche du point supérieur gauche du graphique. Ainsi, l'indicateur objectif de la qualité du classificateur est l'aire sous la courbe ROC (indicateur ROC AUC). La valeur de cet indicateur doit être aussi proche que possible de 1. La valeur AUC de 0,5 correspond à un classificateur aléatoire.

L'AUC de notre modèle (voir la figure ci-dessus) est de 0,57, ce qui est loin d'être le meilleur résultat.



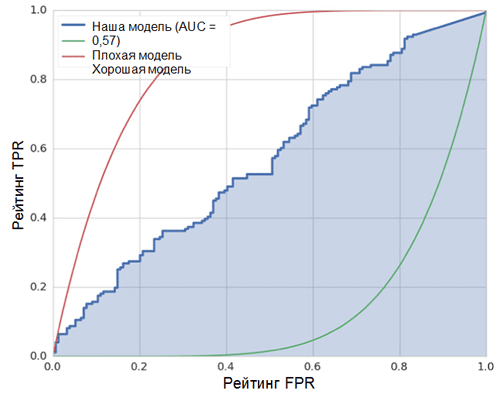
Toutes ces mesures indiquent que le modèle résultant n'est que légèrement meilleur que le classificateur aléatoire. Il y a plusieurs raisons à cela, les principales sont décrites ci-dessous:

• Très petite quantité de données pour la formation, insuffisante pour mettre en évidence les traits caractéristiques des images. Même l'augmentation des données ne pouvait pas aider dans ce cas.
• Un modèle de réseau de neurones convolutionnel relativement complexe (par rapport à d'autres modèles d'apprentissage automatique) avec un grand nombre de paramètres.

Conclusion

Dans cet article, nous avons créé un modèle de réseau de neurones convolutionnel simple pour reconnaître les émotions dans les images. Dans le même temps, au stade de la formation, un certain nombre de méthodes ont été utilisées pour augmenter les données, et le modèle a également été évalué à l'aide d'un ensemble de paramètres tels que la précision, la courbe ROC, l'AUC ROC et la matrice d'imprécision. Le modèle a montré des résultats, seulement quelques-uns des meilleurs aléatoires. .