Le principe de moindre action. Partie 1

Quand j'ai appris ce principe pour la première fois, j'ai ressenti une sorte de mysticisme. Il semble que la nature parcourt mystérieusement tous les chemins possibles du système et en sélectionne le meilleur.

Aujourd'hui, je veux parler un peu de l'un des principes physiques les plus remarquables - le principe de la moindre action.

Contexte

Depuis l'époque de Galilée, on savait que les corps qui ne sont affectés par aucune force se déplacent en ligne droite, c'est-à-dire le long du chemin le plus court. Les rayons lumineux se propagent en lignes droites.

Lorsqu'elle est réfléchie, la lumière se déplace également de manière à se déplacer d'un point à un autre de la manière la plus courte. Dans l'image, le chemin le plus court sera le chemin vert auquel l'angle d'incidence est égal à l'angle de réflexion. Tout autre chemin, comme le rouge, sera plus long.


Ceci est facile à prouver en reflétant simplement les trajets des rayons vers le côté opposé du miroir. Dans l'image, ils sont représentés par une ligne pointillée.


On peut voir que le chemin vert de l'ACB se transforme en ACB direct '. Et le chemin rouge se transforme en une ligne brisée ADB ', qui, bien sûr, est plus longue que le vert.

En 1662, Pierre Fermat suggère que la vitesse de la lumière dans une substance dense, par exemple dans le verre, est inférieure à celle de l'air. Avant cela, il existait une version généralement acceptée de Descartes, selon laquelle la vitesse de la lumière dans la matière devait être supérieure à celle de l'air afin d'obtenir la bonne loi de réfraction. Pour Fermat, l'hypothèse selon laquelle la lumière peut se déplacer plus rapidement dans un milieu plus dense que dans un milieu raréfié ne semblait pas naturelle. Par conséquent, il a suggéré que tout était exactement le contraire et s'est révélé une chose étonnante - dans cette hypothèse, la lumière est réfractée de manière à atteindre sa destination dans les plus brefs délais.


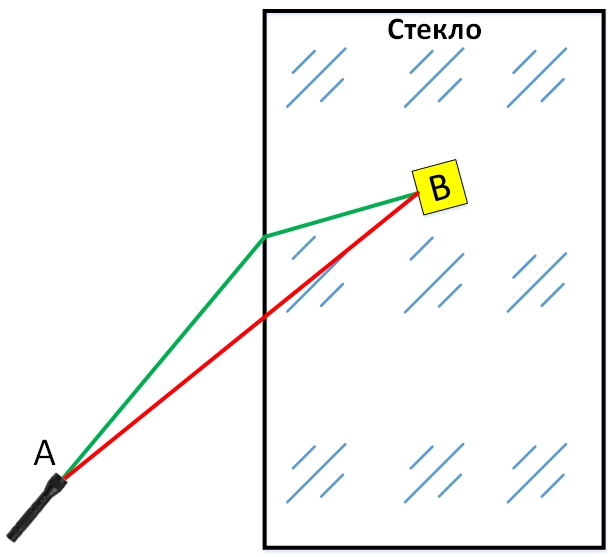
Dans la figure à nouveau, la couleur verte montre le chemin le long duquel le faisceau lumineux se déplace réellement. Le chemin marqué en rouge est le plus court, mais pas le plus rapide, car la lumière a un plus grand chemin pour traverser le verre et sa vitesse y est plus lente. Le plus rapide est le vrai chemin du faisceau lumineux.

Tous ces faits suggèrent que la nature agit de manière rationnelle, que la lumière et les corps se déplacent de manière optimale, en dépensant le moins d'efforts possible. Mais quel genre d'effort il s'agissait, et comment le compter, restait un mystère.

En 1744, Maupertuis introduit le concept «d'action» et formule le principe selon lequel la véritable trajectoire d'une particule diffère de toute autre en ce que son action est minimale. Cependant, Maupertuis lui-même n'a pas pu donner une définition claire de ce à quoi cette action équivaut. La formulation mathématique stricte du principe de moindre action a déjà été développée par d'autres mathématiciens - Euler, Lagrange, et a finalement été donnée par William Hamilton:


En langage mathématique, le principe de moindre action est formulé assez brièvement, mais tous les lecteurs ne peuvent pas comprendre le sens de la notation utilisée. Je veux essayer d'expliquer ce principe plus clairement et en termes simples.

Corps libre

Alors imaginez que vous êtes assis dans une voiture à un moment donné $$ et au moment $$ On vous a confié une tâche simple: au moment où $$ vous devez vous rendre au point en voiture $$ .


Le carburant pour la voiture coûte cher et, bien sûr, vous voulez le dépenser le moins possible. Votre voiture est fabriquée à l'aide des dernières super technologies et peut accélérer ou freiner aussi rapidement que vous le souhaitez. Cependant, il est conçu pour que plus il va vite, plus il consomme de carburant. De plus, la consommation de carburant est proportionnelle au carré de la vitesse. Si vous conduisez deux fois plus vite, vous consommez 4 fois plus de carburant pendant la même période. En plus de la vitesse, la masse de la voiture affecte également la consommation de carburant. Plus notre voiture est lourde, plus elle consomme de carburant. La consommation de carburant de notre voiture à tout moment est $$ , c'est-à-dire exactement l'énergie cinétique de la voiture.

Alors, comment devez-vous aller pour arriver au point $$ à l'heure exacte et utiliser le moins possible de carburant? Il est clair que vous devez aller en ligne droite. Avec une augmentation de la distance de conduite, le carburant sera consommé exactement pas moins. Et puis vous pouvez choisir différentes tactiques. Par exemple, vous pouvez rapidement en venir au point $$ à l'avance et asseyez-vous, attendez, le moment venu $$ . La vitesse de conduite, et donc la consommation de carburant à un moment donné, se révélera importante, mais le temps de conduite sera également réduit. Peut-être que la consommation totale de carburant dans ce cas ne sera pas si grande. Ou vous pouvez rouler de manière uniforme, à la même vitesse, de telle sorte que, sans se précipiter, il suffit d'arriver à la fois $$ . Ou une partie du chemin pour conduire vite et en partie plus lentement. Quelle meilleure façon de procéder?

Il s’avère que la façon la plus optimale et la plus économique de conduire est de conduire à vitesse constante, $$ à l'heure exacte fixée $$ . Avec toute autre option, le carburant sera consommé davantage. Vous pouvez le vérifier vous-même avec quelques exemples. La raison en est que la consommation de carburant augmente proportionnellement au carré de la vitesse. Par conséquent, à mesure que la vitesse augmente, la consommation de carburant augmente plus rapidement que le temps de conduite diminue, et la consommation globale de carburant augmente également.

Ainsi, nous avons découvert que si une voiture à un moment donné consomme du carburant proportionnellement à son énergie cinétique, alors le moyen le plus économique de se rendre d'un point $$ au point $$ à un moment précis est de rouler de façon uniforme et rectiligne, tout comme un corps se déplace en l'absence de forces agissant sur lui. Toute autre façon de conduire entraînera une consommation globale de carburant plus élevée.

En gravité

Maintenant, améliorons un peu notre voiture. Fixons-y des moteurs à réaction pour qu'il puisse voler librement dans toutes les directions. En général, la conception est restée la même, de sorte que la consommation de carburant est restée strictement proportionnelle à l'énergie cinétique de la voiture. Si maintenant la tâche est donnée de voler hors du point $$ au moment $$ et vole au point $$ par le temps $$ , alors le moyen le plus économique, comme précédemment, bien sûr, volera de manière uniforme et rectiligne, pour être à un point $$ à l'heure exacte fixée $$ . Cela correspond à nouveau à la libre circulation du corps dans l'espace tridimensionnel.


Cependant, un appareil inhabituel a été installé dans le dernier modèle de voiture. Cette unité peut produire du carburant littéralement à partir de rien. Mais la conception est telle que plus la voiture est haute, plus l'appareil génère de carburant à chaque instant. La production de carburant est directement proportionnelle à la hauteur $$ sur lequel se trouve actuellement la voiture. De plus, plus la voiture est lourde, plus l'appareil est puissant et plus il produit de carburant, et la sortie est directement proportionnelle à la masse de la voiture $$ . L'appareil s'est avéré de sorte que la production de carburant est exactement égale $$ (où $$ - accélération de la gravité), c'est-à-dire énergie potentielle de la voiture.

La consommation de carburant à chaque instant est égale à l'énergie cinétique moins l'énergie potentielle de la voiture (moins l'énergie potentielle, car l'appareil installé génère du carburant et ne dépense pas). Maintenant, notre tâche est le mouvement de voiture le plus économique entre les points $$ et $$ devient plus difficile. Le mouvement uniforme rectiligne n'est dans ce cas pas le plus efficace. Il s'avère qu'il est plus optimal de prendre un peu d'altitude, de s'y attarder un moment, après avoir développé plus de carburant, puis de descendre au point $$ . Avec la bonne trajectoire de vol, la production totale de carburant due à la montée bloquera la consommation de carburant supplémentaire en augmentant la longueur de la trajectoire et en augmentant la vitesse. Si vous calculez soigneusement, alors de la manière la plus économique pour une voiture, elle volera le long d'une parabole, exactement le long d'une telle trajectoire et exactement à la même vitesse qu'une pierre volerait dans le champ de gravité de la Terre.


Une explication mérite d'être faite ici. Bien sûr, vous pouvez du point $$ jeter une pierre de différentes manières pour qu'elle atteigne un point $$ . Mais vous devez le lancer pour qu'il vole hors de propos $$ au moment $$ frapper le point $$ exactement au moment $$ . Ce mouvement sera le plus économique pour notre voiture.

Fonction de Lagrange et principe de moindre action

Maintenant, nous pouvons transférer cette analogie à de vrais corps physiques. Un analogue de l'intensité de consommation de carburant pour les corps est appelé la fonction de Lagrange ou Lagrangien (en l'honneur de Lagrange) et est désigné par la lettre $$ . Lagrangian montre combien de «carburant» le corps consomme à un moment donné. Pour un corps se déplaçant dans un champ potentiel, le lagrangien est égal à son énergie cinétique moins l'énergie potentielle.

Un analogue de la quantité totale de carburant consommé pendant toute la durée du mouvement, c'est-à-dire la valeur du lagrangien accumulée pendant toute la durée du mouvement est appelée «action».

Le principe de moindre action est que le corps bouge de telle sorte que l'action (qui dépend de la trajectoire du mouvement) soit minimale. Dans le même temps, il ne faut pas oublier que les conditions initiales et finales sont précisées, c'est-à-dire où le corps est à un moment donné $$ et au moment $$ .

De plus, la carrosserie n'a pas à se déplacer dans un champ gravitationnel uniforme, que nous avons envisagé pour notre voiture. Vous pouvez considérer des situations complètement différentes. Le corps peut osciller sur une bande élastique, osciller sur un pendule ou voler autour du Soleil, dans tous ces cas il se déplace de manière à minimiser la «consommation totale de carburant» c'est-à-dire action.

Si le système est composé de plusieurs corps, alors le lagrangien d'un tel système sera égal à l'énergie cinétique totale de tous les corps moins l'énergie potentielle totale de tous les corps. Et encore une fois, tous les corps se déplaceront de manière coordonnée afin que l'action de l'ensemble du système avec un tel mouvement soit minimale.

Pas si simple

En fait, j'ai un peu triché en disant que les corps bougent toujours de manière à minimiser l'action. Bien que cela soit vrai dans de nombreux cas, vous pouvez trouver des situations dans lesquelles l'action n'est clairement pas minimale.

Par exemple, prenez une balle et placez-la dans un espace vide. A une certaine distance de celui-ci, nous mettons une paroi élastique. Supposons que nous voulons que la balle soit au même endroit après un certain temps. Dans de telles conditions, le ballon peut se déplacer de deux manières différentes. Premièrement, il peut simplement rester en place. Deuxièmement, il peut être poussé vers le mur. La balle va voler contre le mur, rebondir et revenir. Il est clair que vous pouvez le pousser si vite qu'il revient exactement au bon moment.


Les deux variantes du mouvement de la balle sont possibles, mais l'action dans le deuxième cas se révélera plus, car pendant tout ce temps, la balle se déplacera avec une énergie cinétique non nulle.

Comment sauvegarder le principe de moindre action pour qu'il soit juste dans de telles situations? Nous en reparlerons la prochaine fois .