Calcul d'intégrales définies: algorithmes de base

Cette publication décrit les méthodes les plus simples pour calculer les intégrales des fonctions d'une variable sur un segment, également appelées formules de quadrature. En règle générale, ces méthodes sont implémentées dans des bibliothèques mathématiques standard telles que la bibliothèque scientifique GNU pour C, SciPy pour Python et autres. La publication vise à démontrer comment ces méthodes fonctionnent "sous le capot" et à attirer l'attention sur certains problèmes de précision et de performance des algorithmes. Je voudrais également noter la relation entre les formules en quadrature et les méthodes d'intégration numérique des équations différentielles ordinaires, à propos desquelles je veux écrire une autre publication.

Définition de l'intégrale

Intégrale (selon Riemann) d'une fonction $$$f (x)$ sur le segment $$$[a; b]$ La limite suivante est appelée:

où $$$\ Delta x = \ max \ lbrace x_ {i + 1} - x_i \ rbrace$ - finesse de la partition, $$$x_0 = a$ , $$$x_n = b$ , $$$\ xi_i$ - un nombre arbitraire sur le segment $$$[x_i; x_ {i + 1}]$ .

Si l'intégrale de la fonction existe, alors la valeur limite est la même quelle que soit la partition, si seulement elle était suffisamment petite.

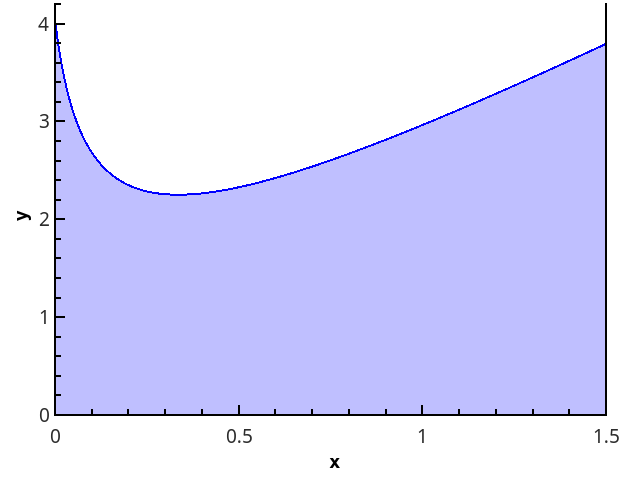
La définition géométrique est plus claire - l'intégrale est égale à l'aire du trapèze courbe délimitée par l'axe 0 x , le graphique de la fonction et les lignes droites x = a et x = b (région remplie sur la figure).

Formules en quadrature

La définition de l'intégrale (1) peut être réécrite sous la forme

où $$$w_i$ - coefficients de pondération, dont la somme doit être égale à 1, et les coefficients eux-mêmes - tendent à zéro avec un nombre croissant $$$n$ points auxquels la fonction est calculée.

L'expression (2) est la base de toutes les formules en quadrature (c'est-à-dire les formules pour le calcul approximatif de l'intégrale). Le défi est de sélectionner des points $$$\ lbrace \ xi_i \ rbrace$ et poids $$$w_i$ de sorte que la somme du côté droit se rapproche le plus précisément possible de l'intégrale requise.

Tâche de calcul

Ensemble de fonctions $$$f (x)$ pour lequel il existe un algorithme de calcul des valeurs à tout moment de l'intervalle $$$[a; b]$ (Je veux dire les points représentés par un nombre à virgule flottante - il n'y a pas de fonctions Dirichlet là-bas!).

Il est nécessaire de trouver la valeur approximative de l'intégrale $$$\ int_a ^ b f (x) dx$ .
Les solutions seront implémentées dans Python 3.6.

Pour vérifier les méthodes, utilisez l'intégrale $$$\ int_0 ^ {3/2} \ left [2x + \ frac {1} {\ sqrt {x + 1/16}} \ right] dx = 17/4$ .

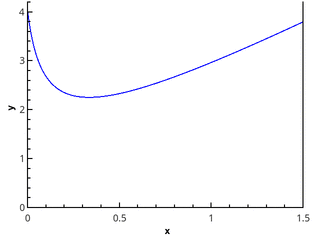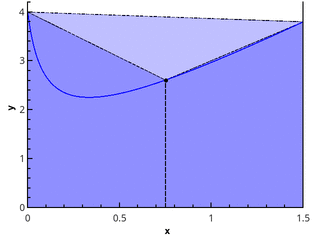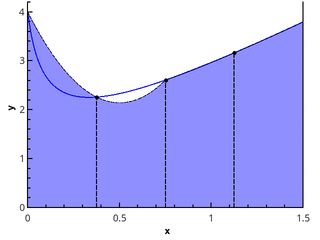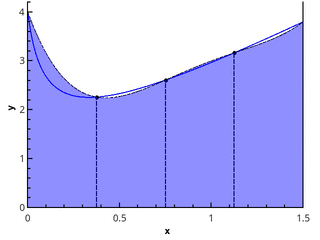
Approximation constante par morceaux

Les formules de quadrature idéalement simples résultent de l'application de l'expression (1) "au front":

Parce que de la méthode de division d'un segment par des points $$$\ lbrace x_i \ rbrace$ et sélectionnez des points $$$\ lbrace \ xi_i \ rbrace$ la valeur limite ne dépend pas, alors nous les choisissons pour qu'elles puissent être facilement calculées - par exemple, nous prenons la partition uniformément, et pour les points de calcul de la fonction nous considérons les options: 1) $$$\ xi_i = x_i$ ; 2) $$$\ xi_i = x_ {i + 1}$ ; 3) $$$\ xi_i = (x_i + x_ {i + 1}) / 2$ .

Nous obtenons respectivement les méthodes des rectangles de gauche, des rectangles de droite et des rectangles avec un milieu.

def _rectangle_rule(func, a, b, nseg, frac): """  .""" dx = 1.0 * (b - a) / nseg sum = 0.0 xstart = a + frac * dx # 0 <= frac <= 1    , #    , #     dx for i in range(npoints): sum += func(xstart + i * dx) return sum * dx def left_rectangle_rule(func, a, b, nseg): """  """ return _rectangle_rule(func, a, b, nseg, 0.0) def right_rectangle_rule(func, a, b, nseg): """  """ return _rectangle_rule(func, a, b, npoints, 1.0) def midpoint_rectangle_rule(func, a, b, nseg): """    """ return _rectangle_rule(func, a, b, nseg, 0.5) 

Pour analyser les performances des formules en quadrature, nous construisons un graphique de l'erreur dans les coordonnées "le nombre de points est la différence entre le résultat numérique et l'exact".

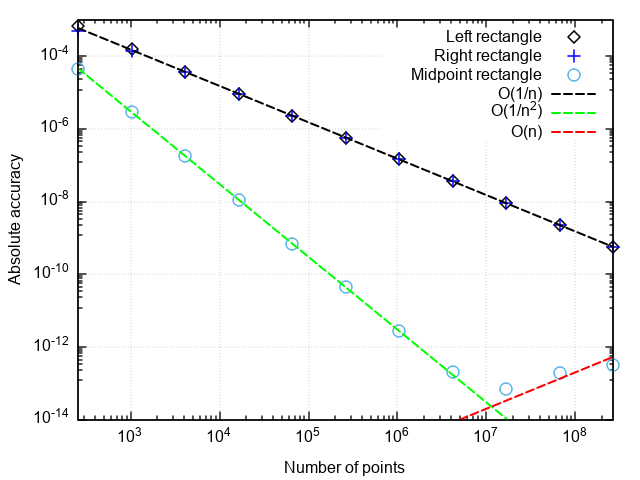
Ce que vous pouvez remarquer:

1. Une formule avec un point médian est beaucoup plus précise qu'avec un point droit ou gauche
2. L'erreur de la formule avec le milieu tombe plus vite que les deux autres
3. Avec une très petite partition, l'erreur de la formule avec le milieu commence à augmenter
   Les deux premiers points sont liés au fait que la formule des rectangles avec un milieu a un deuxième ordre d'approximation, c'est-à-dire $$$| I_n - I | = O (1 / n ^ 2)$ , et les formules des rectangles droit et gauche sont du premier ordre, c'est-à-dire $$$| I_n - I | = O (1 / n)$ .
   Une augmentation de l'erreur lors du broyage de l'étape d'intégration est associée à une augmentation de l'erreur d'arrondi lors de la sommation d'un grand nombre de termes. Cette erreur se développe comme $$$| I_n - I | = O (1 / n)$ cela ne permet pas l'intégration pour atteindre la précision de la machine.
   Conclusion: les méthodes des rectangles à points droit et gauche ont une faible précision, qui croît aussi lentement avec le raffinement de la partition. Par conséquent, ils n'ont de sens qu'à des fins de démonstration. La méthode des rectangles avec un point médian a un ordre d'approximation plus élevé, ce qui lui donne une chance d'être utilisé dans des applications réelles (plus de détails ci-dessous).

Approximation linéaire par morceaux

L'étape logique suivante consiste à approximer la fonction intégrable sur chacun des sous-segments par une fonction linéaire, qui donne la formule en quadrature des trapèzes:

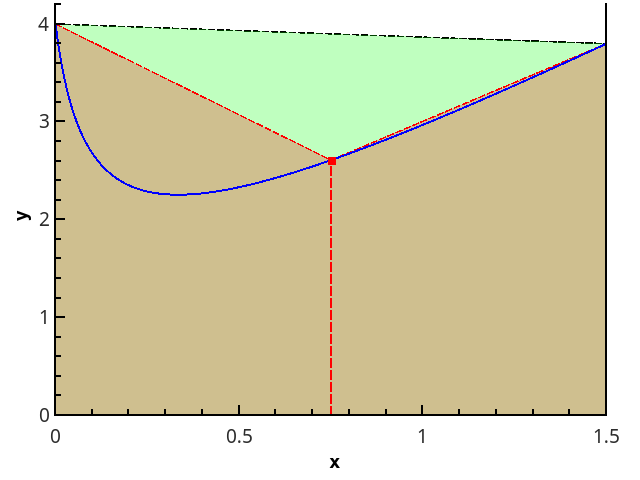
Illustration de la méthode trapézoïdale pour n = 1 et n = 2.

Dans le cas d'une grille uniforme, les longueurs de tous les segments de la partition sont égales et la formule a la forme

 def trapezoid_rule(func, a, b, nseg): """  nseg -  ,    [a;b]""" dx = 1.0 * (b - a) / nseg sum = 0.5 * (func(a) + func(b)) for i in range(1, nseg): sum += func(a + i * dx) return sum * dx 

Après avoir tracé l'erreur en fonction du nombre de points de partage, nous voyons que la méthode trapézoïdale a également un second ordre d'approximation et donne généralement des résultats légèrement différents de la méthode du rectangle médian (ci-après simplement la méthode du rectangle).

Contrôle de précision de calcul

Définir le nombre de points de partage comme paramètre d'entrée n'est pas très pratique, car il est généralement nécessaire de calculer l'intégrale non pas avec une densité de partition donnée, mais avec une erreur donnée. Si l'intégrande est connue à l'avance, alors nous pouvons estimer l'erreur à l'avance et choisir une étape d'intégration telle que la précision spécifiée est certainement atteinte. Mais c'est rarement le cas dans la pratique (et en général, n'est-il pas plus facile, avec la fonction connue à l'avance, d'intégrer l'intégrale à l'avance?), Par conséquent, une procédure d'ajustement automatique du pas à une erreur donnée est nécessaire.

Comment mettre cela en œuvre? Une des méthodes simples pour estimer l'erreur - la règle de Runge - la différence dans les valeurs des intégrales calculées à partir de n et 2 n points, donne une estimation d'erreur: $$$\ Delta_ {2n} \ approx | I_ {2n} - I_n |$ . La méthode trapézoïdale est plus pratique pour doubler la finesse d'une partition que la méthode des rectangles avec un point central. Lors du calcul par la méthode trapézoïdale, pour doubler le nombre de points, de nouvelles valeurs de la fonction ne sont nécessaires qu'au milieu des segments de la partition précédente, c'est-à-dire l'approximation précédente de l'intégrale peut être utilisée pour calculer la suivante.

De là, nous obtenons le code suivant pour la méthode trapézoïdale avec contrôle de précision:

 def trapezoid_rule(func, a, b, rtol = 1e-8, nseg0 = 1): """  rtol -     nseg0 -    """ nseg = nseg0 old_ans = 0.0 dx = 1.0 * (b - a) / nseg ans = 0.5 * (func(a) + func(b)) for i in range(1, nseg): ans += func(a + i * dx) ans *= dx err_est = max(1, abs(ans)) while (err_est > abs(rtol * ans)): old_ans = ans ans = 0.5 * (ans + midpoint_rectangle_rule(func, a, b, nseg)) #      #       nseg *= 2 err_est = abs(ans - old_ans) return ans 

Avec cette approche, l'intégrande ne sera pas calculée plusieurs fois à un moment donné, et toutes les valeurs calculées sont utilisées pour le résultat final.

Mais est-il possible d'obtenir une précision plus élevée avec le même nombre de calculs de fonction? Il s'avère que c'est possible, il existe des formules qui fonctionnent plus précisément que la méthode trapézoïdale sur la même grille.

Approximation parabolique par morceaux

L'étape suivante consiste à approximer la fonction avec des éléments paraboliques. Cela nécessite que le nombre de segments de la partition soit pair, puis les paraboles peuvent être tracées à travers des triplets de points avec des abscisses {( x ₀ = a , x ₁ , x ₂ ), ( x ₂ , x ₃ , x ₄ ), ..., ( x _{n -2} , x _{n -1} , x _n = b )}.

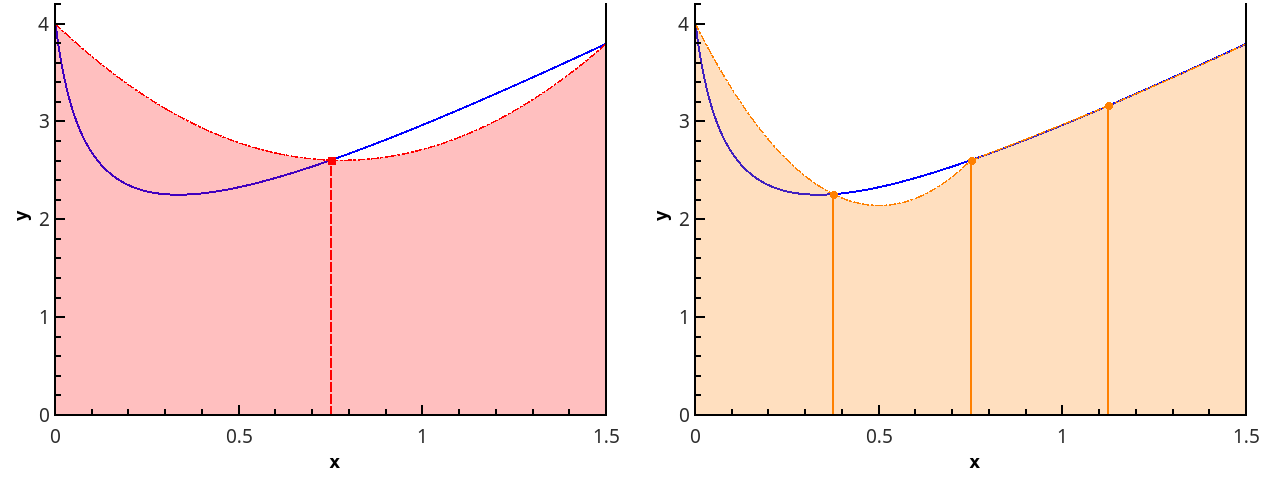
Illustration d'une approximation parabolique par morceaux à 3 et 5 points ( n = 2 et n = 3).

Approcher l'intégrale de la fonction sur chacun des segments [ x _k ; x _{k +2} ] par l'intégrale de l'approximation parabolique sur ce segment et en supposant que les points sont uniformément répartis ( x _{k +1} = x _k + h ), on obtient la formule de Simpson :

La formule (4) donne directement une implémentation «naïve» de la méthode Simpson:

 def simpson_rule(func, a, b, nseg): """  nseg -  ,    [a;b]""" if nseg%2 = 1: nseg += 1 dx = 1.0 * (b - a) / nseg sum = (func(a) + 4 * func(a + dx) + func(b)) for i in range(1, nseg / 2): sum += 2 * func(a + (2 * i) * dx) + 4 * func(a + (2 * i + 1) * dx) return sum * dx / 3 

Pour estimer l'erreur, vous pouvez utiliser le même calcul de l'intégrale avec les étapes h et h / 2 - mais voici le problème, lors du calcul de l'intégrale avec un pas plus petit, le résultat du calcul précédent devra être ignoré, bien que la moitié des nouveaux calculs de fonction soient aux mêmes points qu'auparavant.

Heureusement, vous pouvez éviter de perdre du temps machine si vous implémentez la méthode Simpson de manière plus ingénieuse. Après avoir regardé de plus près, nous notons que l'intégrale par la formule de Simpson peut être représentée par deux intégrales par la formule trapézoïdale avec des étapes différentes. Cela se voit le plus clairement dans le cas de base de l'approximation de l'intégrale sur trois points $$$(a, f_0), ~ (a + h, f_1), ~ (a + 2h, f_2)$ :

Ainsi, si nous mettons en œuvre la procédure de réduction du pas de moitié et stockons les deux derniers calculs par la méthode trapézoïdale, la méthode Simpson avec contrôle de précision est mise en œuvre plus efficacement.

 class Quadrature: """    """ __sum = 0.0 __nseg = 1 #    __ncalls = 0 #      def __restart(func, x0, x1, nseg0, reset_calls = True): """    .       """ if reset_calls: Quadrature.__ncalls = 0 Quadrature.__nseg = nseg0 #           nseg0 Quadrature.__sum = 0.5 * (func(x0) + func(x1)) dx = 1.0 * (x1 - x0) / nseg0 for i in range(1, nseg0): Quadrature.__sum += func(x0 + i * dx) Quadrature.__ncalls += 1 + nseg0 return Quadrature.__sum * dx def __double_nseg(func, x0, x1): """  .       """ nseg = Quadrature.__nseg dx = (x1 - x0) / nseg x = x0 + 0.5 * dx i = 0 AddedSum = 0.0 for i in range(nseg): AddedSum += func(x + i * dx) Quadrature.__sum += AddedSum Quadrature.__nseg *= 2 Quadrature.__ncalls += nseg return Quadrature.__sum * 0.5 * dx def trapezoid(func, x0, x1, rtol = 1e-10, nseg0 = 1): """     . rtol -  , nseg0 -    """ ans = Quadrature.__restart(func, x0, x1, nseg0) old_ans = 0.0 err_est = max(1, abs(ans)) while (err_est > abs(rtol * ans)): old_ans = ans ans = Quadrature.__double_nseg(func, x0, x1) err_est = abs(old_ans - ans) print("Total function calls: " + str(Quadrature.__ncalls)) return ans def simpson(func, x0, x1, rtol = 1.0e-10, nseg0 = 1): """     . rtol -  , nseg0 -    """ old_trapez_sum = Quadrature.__restart(func, x0, x1, nseg0) new_trapez_sum = Quadrature.__double_nseg(func, x0, x1) ans = (4 * new_trapez_sum - old_trapez_sum) / 3 old_ans = 0.0 err_est = max(1, abs(ans)) while (err_est > abs(rtol * ans)): old_ans = ans old_trapez_sum = new_trapez_sum new_trapez_sum = Quadrature.__double_nseg(func, x0, x1) ans = (4 * new_trapez_sum - old_trapez_sum) / 3 err_est = abs(old_ans - ans) print("Total function calls: " + str(Quadrature.__ncalls)) return ans 

Comparez l'efficacité de la méthode trapézoïdale et parabole:

 >>> import math >>> Quadrature.trapezoid(lambda x: 2 * x + 1 / math.sqrt(x + 1 / 16), 0, 1.5, rtol=1e-9) Total function calls: 65537 4.250000001385811 >>> Quadrature.simpson(lambda x: 2 * x + 1 / math.sqrt(x + 1 / 16), 0, 1.5, rtol=1e-9) Total function calls: 2049 4.2500000000490985 

Comme vous pouvez le voir, avec les deux méthodes, la réponse peut être obtenue avec une précision assez élevée, mais le nombre d'appels à l'intégrande est très différent - une méthode d'ordre supérieur est 32 fois plus efficace!

En traçant l'erreur d'intégration en fonction du nombre d'étapes, nous pouvons vérifier que l'ordre d'approximation de la formule de Simpson est quatre, c'est-à-dire erreur d'intégration numérique $$$| I_ {Simps, n} - I | = O (1 / n ^ 4)$ (et les intégrales des polynômes cubiques utilisant cette formule sont calculées jusqu'aux erreurs d'arrondi pour tout n > 0!).

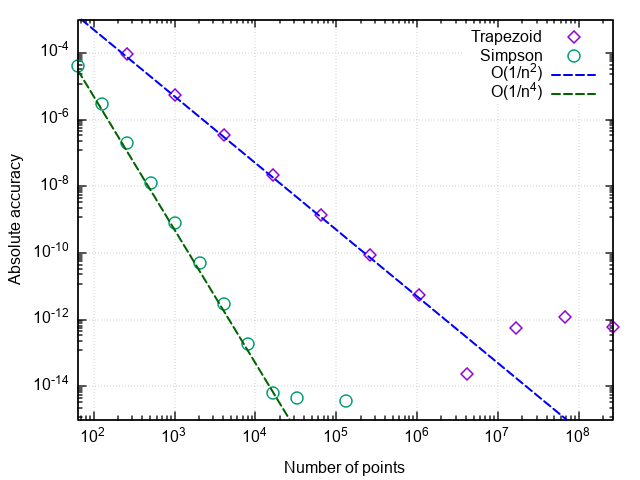
Par conséquent, une telle augmentation de l'efficacité se produit en comparaison avec la formule trapézoïdale simple.

Et ensuite?

La logique supplémentaire d'augmenter la précision des formules en quadrature est généralement compréhensible - si nous continuons à approximer la fonction avec des polynômes d'un degré toujours plus élevé, alors l'intégrale de ces polynômes rapprochera de plus en plus précisément l'intégrale de la fonction d'origine. Cette approche est appelée la construction de formules de Newton-Cotes quadratiques . Des formules contenant jusqu'à 8 ordres d'approximation sont connues, mais les termes alternatifs apparaissent parmi les coefficients de pondération w _i dans (2), et les formules perdent de leur stabilité dans les calculs.

Essayons dans l'autre sens. L'erreur de la formule en quadrature est représentée par une série de puissances de l'étape d'intégration h . Une propriété remarquable de la méthode trapézoïdale (et des rectangles avec un point médian!) Est que pour elle cette série n'est constituée que de degrés pairs:

L'extrapolation de Richardson est basée sur la recherche d'approximations successives de cette expansion: au lieu d'approximer l'intégrande par un polynôme, à partir des approximations calculées de l'intégrale $$$I (h)$ une approximation polynomiale est construite, qui pour h = 0 devrait donner la meilleure approximation à la vraie valeur de l'intégrale.

L'élargissement de l'erreur d'intégration dans les puissances paires de l'étape de partition accélère fortement la convergence de l'extrapolation, car pour l'approximation d'ordre 2 n , seules les valeurs n de l'intégrale sont nécessaires par la méthode trapézoïdale.

Si nous supposons que chaque terme suivant est inférieur au précédent, alors nous pouvons exclure séquentiellement les degrés de h , ayant des approximations intégrales calculées avec différentes étapes. Étant donné que l'implémentation ci-dessus nous permet facilement de diviser la partition en deux, il est pratique de considérer les formules des étapes h et h / 2.

Il est facile de montrer que l'exception du terme supérieur de l'erreur de la formule trapézoïdale donnera exactement la formule de Simpson:

En répétant une procédure similaire pour la formule Simpson, nous obtenons:

Si vous continuez, le tableau suivant se profile:

La première colonne contient les intégrales calculées par la méthode trapézoïdale. Lorsque vous vous déplacez de la ligne supérieure vers le bas, la division du segment devient deux fois plus petite et lorsque vous vous déplacez de la colonne de gauche vers la droite, l'ordre d'approximation de l'intégrale augmente (c'est-à-dire que la deuxième colonne contient les intégrales par la méthode Simpson, etc.)

Les éléments du tableau, comme on peut le déduire de l'expansion (5), sont liés par la relation de récurrence:

L'erreur d'approximation de l'intégrale peut être estimée à partir de la différence de formules de différents ordres sur une seule ligne, c'est-à-dire

L'utilisation de l'extrapolation de Richardson avec l'intégration trapézoïdale est appelée la méthode de Romberg . Si la méthode Simpson prend en compte les deux valeurs précédentes par la méthode trapézoïdale, la méthode Romberg utilise toutes les valeurs précédemment calculées par la méthode trapézoïdale pour obtenir une estimation plus précise de l'intégrale.

 class Quadrature: """    """ __sum = 0.0 __nseg = 1 #    __ncalls = 0 #      def __restart(func, x0, x1, nseg0, reset_calls = True): """    .       """ if reset_calls: Quadrature.__ncalls = 0 Quadrature.__nseg = nseg0 #          nseg0  Quadrature.__sum = 0.5 * (func(x0) + func(x1)) dx = 1.0 * (x1 - x0) / nseg0 for i in range(1, nseg0): Quadrature.__sum += func(x0 + i * dx) Quadrature.__ncalls += 1 + nseg0 return Quadrature.__sum * dx def __double_nseg(func, x0, x1): """  .       """ nseg = Quadrature.__nseg dx = (x1 - x0) / nseg x = x0 + 0.5 * dx i = 0 AddedSum = 0.0 for i in range(nseg): AddedSum += func(x + i * dx) Quadrature.__sum += AddedSum Quadrature.__nseg *= 2 Quadrature.__ncalls += nseg return Quadrature.__sum * 0.5 * dx def romberg(func, x0, x1, rtol = 1e-10, nseg0 = 1, maxcol = 5, reset_calls = True): """   nseg0 -     maxcol -   """ #   Itable = [[Quadrature.__restart(func, x0, x1, nseg0, reset_calls)]] i = 0 maxcol = max(0, maxcol) ans = Itable[i][i] error_est = max(1, abs(ans)) while (error_est > abs(rtol * ans)): old_ans = ans i += 1 d = 4.0 ans_col = min(i, maxcol) Itable.append([Quadrature.__double_nseg(func, x0, x1)] * (ans_col + 1)) for j in range(0, ans_col): diff = Itable[i][j] - Itable[i - 1][j] Itable[i][j + 1] = Itable[i][j] + diff / (d - 1.0) d *= 4.0 ans = Itable[i][ans_col] if (maxcol <= 1): #       error_est = abs(ans - Itable[i - 1][-1]) elif (i > maxcol): error_est = abs(ans - Itable[i][min(i - maxcol - 1, maxcol - 1)]) else: error_est = abs(ans - Itable[i - 1][i - 1]) print("Total function calls: " + str(Quadrature.__ncalls)) return ans 

Vérifions le fonctionnement de l'approximation d'ordre élevé:

 >>> Quadrature.romberg(lambda x: 2 * x + 1 / math.sqrt(x + 1/16), 0, 1.5, rtol=1e-9, maxcol = 0) #  Total function calls: 65537 4.250000001385811 >>> Quadrature.romberg(lambda x: 2 * x + 1 / math.sqrt(x + 1/16), 0, 1.5, rtol=1e-9, maxcol = 1) #  Total function calls: 2049 4.2500000000490985 >>> Quadrature.romberg(lambda x: 2 * x + 1 / math.sqrt(x + 1/16), 0, 1.5, rtol=1e-9, maxcol = 4) Total function calls: 257 4.250000001644076 

Nous sommes convaincus que, par rapport à la méthode parabole, le nombre d'appels à l'intégrande a encore diminué de 8 fois. Avec une augmentation supplémentaire de la précision requise, les avantages de la méthode Romberg deviennent encore plus prononcés:

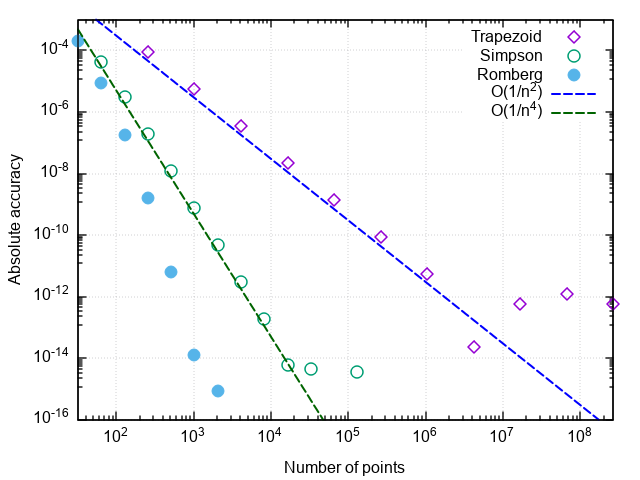
Quelques notes

Remarque 1. Le nombre d'appels de fonction dans ces problèmes caractérise le nombre de sommes lors du calcul de l'intégrale. La réduction du nombre de calculs de l'intégrande permet non seulement d'économiser des ressources informatiques (bien que ce soit également le cas avec une implémentation plus optimisée), mais réduit également l'effet des erreurs d'arrondi sur le résultat. Ainsi, lorsque vous essayez de calculer l'intégrale de la fonction de test, la méthode trapézoïdale se bloque lorsque vous essayez d'obtenir une précision relative de 5 × 10 ^-15 , la méthode parabole - avec la précision souhaitée de 2 × 10 ^-16 (qui est la limite des nombres à double précision), et la méthode Romberg fait face au calcul test intégral jusqu'à la précision de la machine (avec une faible erreur de bit). Autrement dit, non seulement la précision d'intégration est augmentée pour un nombre donné d'appels de fonction, mais également la précision maximale réalisable du calcul de l'intégrale.

Remarque 2. Si la méthode converge lorsqu'une certaine précision est spécifiée, cela ne signifie pas que la valeur calculée de l'intégrale a la même précision. Tout d'abord, cela s'applique aux cas où l'erreur spécifiée est proche de la précision de la machine.

Remarque 3. Bien que la méthode de Romberg pour un certain nombre de fonctions fonctionne de manière presque magique, elle suppose que l'intégrande a borné des dérivées d'ordre élevé. Cela signifie que pour les fonctions avec des plis ou des ruptures, cela peut s'avérer pire que les méthodes simples. Par exemple, intégrez f ( x ) = | x |:

 >>> Quadrature.trapezoid(abs, -1, 3, rtol=1e-5) Total function calls: 9 5.0 >>> Quadrature.simpson(abs, -1, 3, rtol=1e-5) Total function calls: 17 5.0 >>> Quadrature.romberg(abs, -1, 3, rtol=1e-5, maxcol = 2) Total function calls: 17 5.0 >>> Quadrature.romberg(abs, -1, 3, rtol=1e-5, maxcol = 3) Total function calls: 33 5.0 >>> Quadrature.romberg(abs, -1, 3, rtol=1e-5, maxcol = 4) Total function calls: 33 5.000001383269357 

Remarque 4. Il peut sembler que plus l'ordre d'approximation est élevé, mieux c'est. En fait, il vaut mieux limiter le nombre de colonnes dans le tableau de Romberg à 4-6. Pour comprendre cela, regardez la formule (6). Le deuxième terme est la différence de deux éléments consécutifs de la j -1ème colonne divisée par environ 4 ^j . Parce que la jième colonne contient des approximations d'une intégrale d'ordre 2 j , alors la différence elle-même est de l'ordre de (1 / n _i ) ^{2 j} ~ 4 ^{- ij} . En tenant compte de la division, ^on obtient ~ 4 ^{- ( i +1) j} ~ 4 ^{- j 2} . C'est-à-dire pour j ~ 7, le deuxième terme de (6) perd sa précision après la réduction des ordres lors de l'ajout de nombres à virgule flottante, et une augmentation de l'ordre d'approximation peut conduire à l'accumulation d'erreurs d'arrondi.

Remarque 5. Les parties intéressées peuvent utiliser les méthodes décrites pour trouver l'intégrale dans l'intérêt. $$$\ int_0 ^ 1 \ sqrt {x} \ sin {x} dx$ et équivalent à lui $$$\ int_0 ^ 1 2t ^ 2 \ sin {t ^ 2} dt$ . Comme on dit, ressentez la différence.

Conclusion

La description et la mise en œuvre des méthodes de base de l'intégration numérique des fonctions sur une grille uniforme sont présentées. Il est démontré comment, à l'aide d'une simple modification, obtenir la classe de formules de quadrature en utilisant la méthode de Romberg sur la base de la méthode trapézoïdale, ce qui accélère considérablement la convergence de l'intégration numérique. La méthode fonctionne bien pour intégrer des fonctions "ordinaires", c'est-à-dire variant faiblement sur l'intervalle d'intégration, n'ayant pas de singularités aux bords du segment (voir remarque 5), oscillations rapides, etc.

( [3] — C++).

Littérature

1. .. , .. . . .: . 1989.
2. J. Stoer, R. Bulirsch. Introduction to Numerical Analysis: Second Edition. Springer-Verlag New York. 1993.
3. WH Press, SA Teukolsky, WT Vetterling, BP Flannery. Numerical Recipes: Third Edition. Cambridge University Press. 2007.