Nous sélectionnons le mot de passe pour le TIN indien en deux secondes, ou pourquoi les mathématiques de force brute

En Inde, il existe un analogue local de notre DCI - «adhar». Le système électronique "eAdhar" y est vissé. Dans eAdhara, chaque lettre est bloquée avec un mot de passe. Et tout irait bien, mais le mot de passe est composé selon un schéma simple: les quatre premières lettres du nom sont des majuscules, plus l'année de naissance.

Quatre lettres majuscules et quatre chiffres. Parmi celles-ci, 2 821 109 909 456 combinaisons peuvent être compilées. Si vous cochez mille combinaisons par seconde, un mot de passe prendra quatre-vingt-dix ans.

Trop long. Pouvons-nous accélérer quelques ( milliards ) fois?

92 ans → 52 jours. Groupe

Avec trois billions de combinaisons, nous en avions un peu plus. Pourtant, le modèle est connu:

([AZ][AZ][AZ][AZ]) ([0–9][0–9][0–9][0–9]) (4  ) (4 ) ( 1) ( 2) 

Compte tenu de ce modèle, des lignes comme S2N65GE1 peuvent être immédiatement S2N65GE1 . Combien de combinaisons obtenez-vous alors?

Le premier groupe comprend quatre caractères alphabétiques. 26 options, 4 positions, on obtient:

4 positions de 10 chiffres, de même:

De cela, nous obtenons le nombre total de combinaisons:

Estimons à quel point la force brute sera désormais plus rapide. Encore une fois, nous procédons à partir de 1000 tentatives par seconde:

Ou 52 jours, 21 heures, 22 minutes et 40 secondes. Au lieu de 92 ans. Pas mal. Mais encore longtemps. Que peut-on faire d'autre? La même chose - réduisez le nombre de combinaisons.

52 jours → 12 heures. Allumez le bon sens

Le premier et le deuxième groupe ne sont pas un ensemble aléatoire de caractères, mais les premières lettres du nom et de l'année de naissance. Commençons par l'année de naissance.

Cela n'a aucun sens de sélectionner des mots de passe pour ceux nés en 1642 ou 2594. Ainsi, la gamme de combinaisons peut être réduite en toute sécurité de 0000–9999 à 1918–2018. Nous couvrirons donc le plus ou le moins de tous ceux qui vivent entre 0 et 100 ans. Grâce à cela, le nombre de combinaisons et le temps sont respectivement réduits:

Ou 12 heures, 41 minutes et 37 secondes.

12 heures → 2 minutes. Nous sacrifions la précision

12 heures c'est bien, mais ... Il faut aller plus loin .

Nous avons maintenant 45 millions de combinaisons qui couvrent avec précision tous les utilisateurs d'eAdhara. Mais que se passe-t-il si vous leur sacrifiez une petite fraction pour augmenter la vitesse?

Nous avons perfectionné les combinaisons numériques. Les lettres font quelque chose de similaire. La logique est simple: il n'y a pas d'année de naissance 9999, et de la même manière il n'y a pas de nom indien avec «AAAA» au début. Mais comment déterminer toutes les combinaisons appropriées?

J'ai collecté des noms indiens sur le site du catalogue, Photon m'a beaucoup aidé dans ce domaine. Le résultat est 3 283 noms uniques. Il reste à couper les quatre premières lettres et à supprimer les doublons:

 grep -oP ”^\w{4}” custom.txt | sort | uniq | dd conv=ucase 

Il s'est avéré 1598 préfixes! Il y avait pas mal de doublons, car les quatre premières lettres de noms comme «Sanjeev» et «Sanjit» sont les mêmes.

1 598 préfixes - pas assez pour un milliard et demi de personnes? Je suis d'accord. Mais n'oubliez pas que ce sont des préfixes, pas des noms. J'ai posté la liste résultante sur Gist . En fait, il devrait y en avoir plus. Vous pouvez être confus, collecter 10 000 noms sur d'autres sites et obtenir 3 000 préfixes uniques, mais je n'ai pas eu le temps pour cela. Nous allons donc partir de 1598.

Calculons le temps nécessaire maintenant:

Ou 2 minutes et 39,8 secondes.

2 minutes → 2 secondes. Wikipédia à la rescousse

2 minutes 40 secondes est le temps qu'il faudra pour trier toutes les combinaisons. Mais que faire si la onzième combinaison est correcte? Ou le dernier? Ou le premier?

Maintenant, la liste des combinaisons est triée par ordre alphabétique. Mais cela ne sert à rien - qui a dit que les noms sur "A" sont plus courants que sur "B", ou qu'il y a plus d'enfants d'un an que de soixante-dix ans?

Il est nécessaire de considérer la probabilité de chaque combinaison. Sur Wikipédia, ils écrivent:

En Inde, plus de 50% de la population a moins de 25 ans et plus de 65% a moins de 35 ans.

Sur cette base, au lieu de la liste 1–100, vous pouvez essayer ceci:

 25–01 (  ,       ,     ) 25–35 36–100 

Il s'avère ensuite que la probabilité de la première $$ combinaisons augmente à 50%. Nous avons craqué la moitié des mots de passe pour $$ secondes! Dans la suite $$ secondes, nous récupèrerons 15% de mots de passe supplémentaires. Total - 65% des mots de passe en 55,9 secondes.

Passons maintenant aux noms.

Dans Google, il est facile de trouver les noms TOP-100 de n'importe quel pays. Sur la base des données de l'Inde, j'ai déplacé les combinaisons appropriées en haut de la liste. Nous supposons que 15% de la population de l'Inde porte des noms populaires. Ainsi, 15% des mots de passe peuvent être piratés presque instantanément.

Hindous - 80% de la population de l'Inde. Donc, si vous mettez les noms hindous ci-dessus dans la liste, cela accélérera 80% des tentatives. Après l'étape précédente, nous avons quitté $$ tentatives. Si 80% d'entre eux sont des noms hindous, alors 79% (nous laissons 1% pour les noms populaires, mais pas hindous), nous craquerons dans les 65% des tentatives suivantes.

Comptons tout ensemble, en tenant compte des statistiques d'âge. Divisez en groupes:

 100:   { 50:  00  25  { 7:  , 43:   { 34: , 9:   } } 15:  26  35  { 3:  , 13*:   { 10: , 3:   } } 45:  36  100  { 7:  , 38:   { 30: , 8:   } } } 

Maintenant, créons un algorithme efficace pour casser les mots de passe:

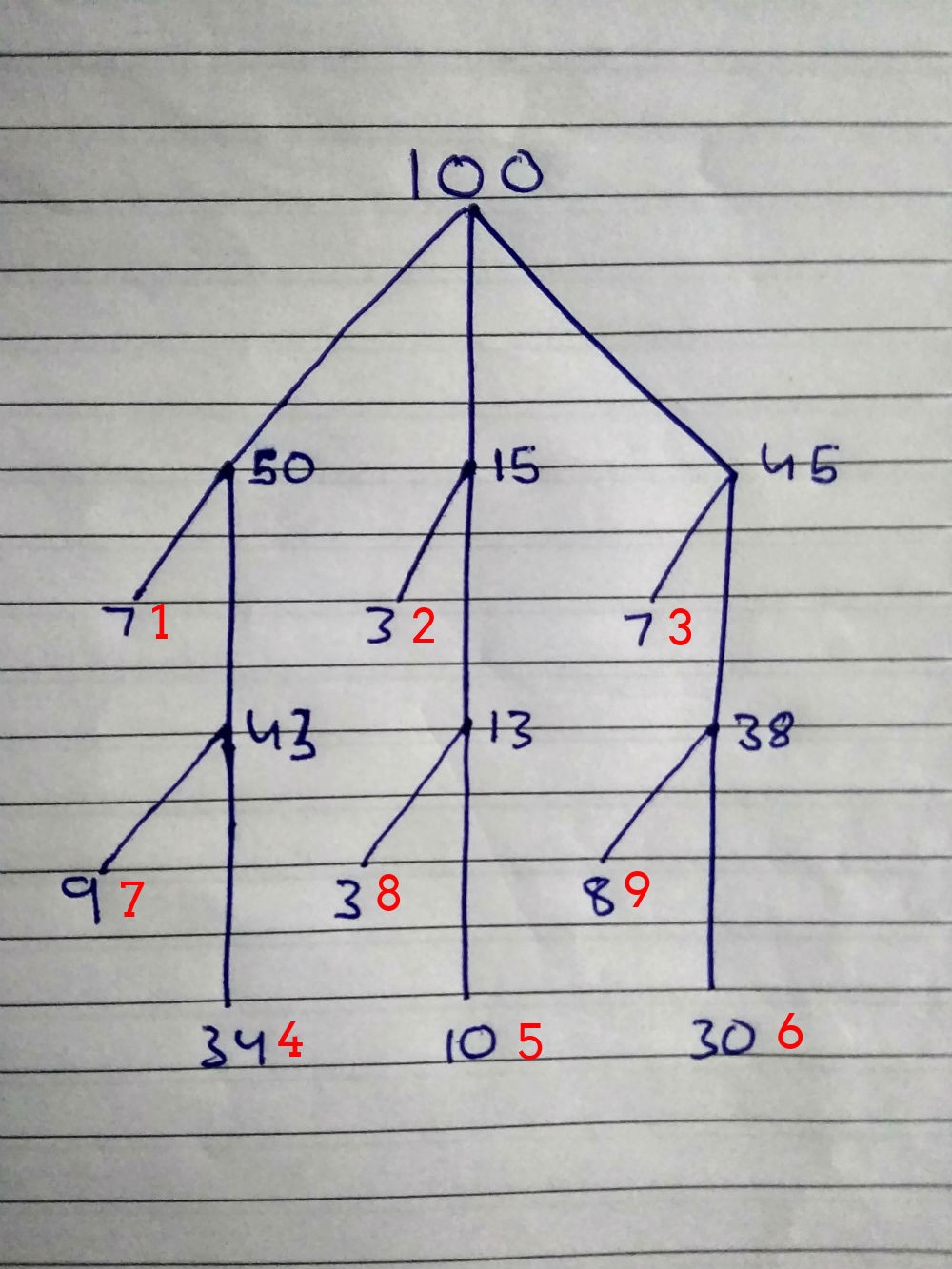
Les chiffres rouges sont une priorité de recherche. Les combinaisons pour les personnes du premier groupe sont testées en premier, puis en deuxième, puis en troisième et ainsi de suite.

Combien de temps faut-il pour pirater maintenant?

Phase 1
1 = 11 secondes pour casser 7 mots de passe
2 = 3 secondes pour déchiffrer 3 mots de passe
3 = 11 secondes pour déchiffrer 7 mots de passe

Nous avons déchiffré les mots de passe de 17 personnes, il en restait 83. Nous allons supprimer les combinaisons précédentes de la liste et essayer les ensembles suivants - 4, 5, 6.

Phase 2
4 = 54 secondes pour déchiffrer 34 mots de passe
5 = 16 secondes pour déchiffrer 10 mots de passe
6 = 47 secondes pour déchiffrer 30 mots de passe

Encore une fois, supprimez les combinaisons des phases précédentes.

Phase 3
7 = 14 secondes pour casser 9 mots de passe
8 = 5 secondes pour déchiffrer 3 mots de passe
9 = 12 secondes pour casser 8 mots de passe

Durée totale : $$ secondes ou 2 minutes et 13 secondes.

Mots de passe craqués : 100

Temps moyen pour un mot de passe : $$ secondes.

92 ans → 1,73 secondes. Nitsche donc, non?