
Préparez-vous, un article extrêmement pédant vous attend, ce qui pourrait bien vous faire économiser une interview ou gagner quelques heures tout en attrapant un bug en production!
Je travaille activement sur la deuxième saison
de The Impostor's Guide et j'écris sur le chiffrement RSA pour SSH, qui est évidemment le code le plus téléchargé de l'histoire de l'informatique.
Je voudrais bien comprendre cette histoire. Qui a inventé ce code, comment il fonctionne, pourquoi il fonctionne et
s'il fonctionnera à l'avenir . Maintenant, j'ai déniché une
putain d'histoire intéressante . Je ne suis pas un cryptomane et j'en vois d'autres littéralement aspirer dans ce domaine. Mais cela m'intéresse aussi, car il y a des petits visons partout, et comme les pies, je suis
attiré par les petites
choses brillantes des visons profonds . Je suis également très doué pour les métaphores.
En tout cas: la semaine dernière, j'ai appris quelque chose d'étrange et je veux partager: il s'avère que le
mod et le reste de la division ne sont pas la même chose . C'est vraiment drôle que certains lecteurs sautent de leurs sièges et crient à ces mots: "Mais c'est exactement ce que j'ai toujours essayé de vous dire, à vous et à tous les autres!"
Appelez les gars de la secte "le mod n'est pas le reste"! C'est pour toi.
Qu'est-ce que le mod?
J'ai dû étudier cela, ainsi que la dernière fois qu'un tel sujet est apparu. C’est l’une de ces choses que vous
connaissez mais dont vous ne vous souvenez pas. Lorsque vous utilisez le mod, divisez un nombre par un autre et prenez le reste. Donc:
5 mod 2 sera 1, car 5/2 = 2 avec le reste de 1.
Le terme mod signifie fonctionnement
modulo , avec le module 2 dans ce cas. La plupart des langages de programmation utilisent
% pour désigner une telle opération:
5 % 2 = 1 .
C'est là que nous entrons dans l'étrange zone grise.
Les mathématiques du cadran
Je me souviens comment j'ai enseigné cela à l'école, puis j'ai oublié. Il existe un type de mathématiques appelé «arithmétique modulaire» qui traite des structures cycliques. La façon la plus simple d'imaginer cela est un cadran avec cycle 12. Pour un mathématicien, le cadran est le
mod 12 . Si vous voulez comprendre s'il est possible de diviser également 253 heures en jours, vous pouvez appliquer l'opération
253 mod 24 , le
résultat sera 13 , donc la réponse est non! Nous ne pouvons répondre oui que si le résultat est 0.
Une autre question que vous pouvez poser est: "Si je pars à 18 heures, quelle heure sera-t-il à votre arrivée dans 16 heures?" Ce sera
6 + 16 mod 12 , soit 10.
Les cryptographes adorent le
mod , car lorsqu'ils sont utilisés avec de très grands nombres, vous pouvez créer quelque chose appelé «fonctions à sens unique». Ce sont des fonctions spéciales qui permettent de calculer facilement quelque chose dans une direction, mais pas dans le sens contraire.
Si je vous dis que 9 est le résultat de l'équerrage, vous pouvez facilement déterminer quelle était l'entrée 3. Avant de voir l'ensemble du processus du début à la fin. Si je dis que 9 est le résultat du
mod 29 , alors il sera plus difficile de comprendre ce que l'entrée est.
Les cryptographes aiment cette idée car ils peuvent utiliser la division du reste avec des nombres premiers géants pour générer des clés cryptographiques. C'est une histoire complètement différente: si vous voulez en savoir plus, vous pouvez acheter un livre ou, mieux encore,
soutenir mes efforts pour l'écrire .
Cependant, nous ne nous écarterons pas du sujet.
Reste et calcul du cadran
Passons maintenant à l'essentiel: modulo et le reste simple sont les mêmes lorsque les nombres sont positifs, mais diffèrent dans le cas de nombres négatifs.
Considérez la tâche suivante:
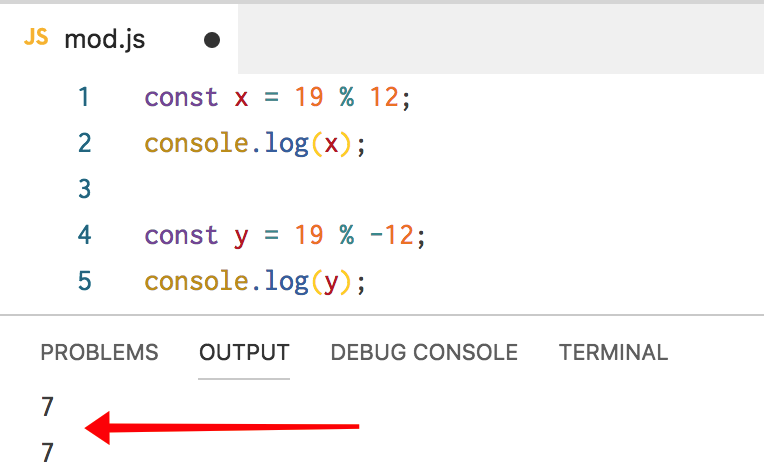
const x = 19 % 12; console.log(x);
Quelle est la valeur de
x ? Divisez les nombres et obtenez 7 comme le reste de 12. C'est la bonne réponse. Que diriez-vous de ceci:
const y = 19 % -12; console.log(y);
En utilisant les mathématiques ordinaires, nous pouvons multiplier -12 par -1, ce qui donne 12, et il nous reste encore 7, donc notre réponse est à nouveau 7.
JavaScript est d'accord avec ceci:
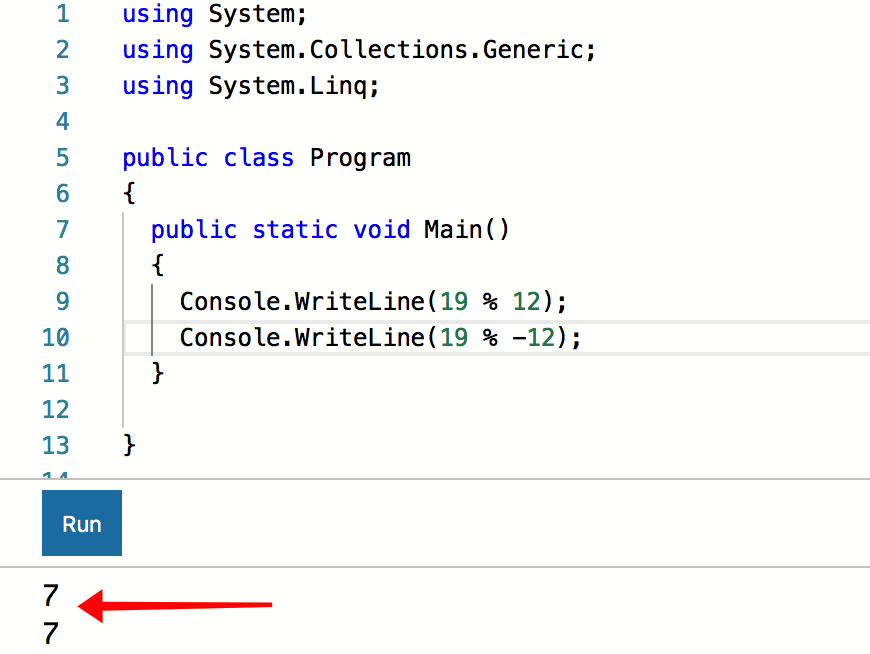
C # accepte aussi:
Google est d'accord avec la première déclaration, mais n'est pas d'accord avec la seconde:
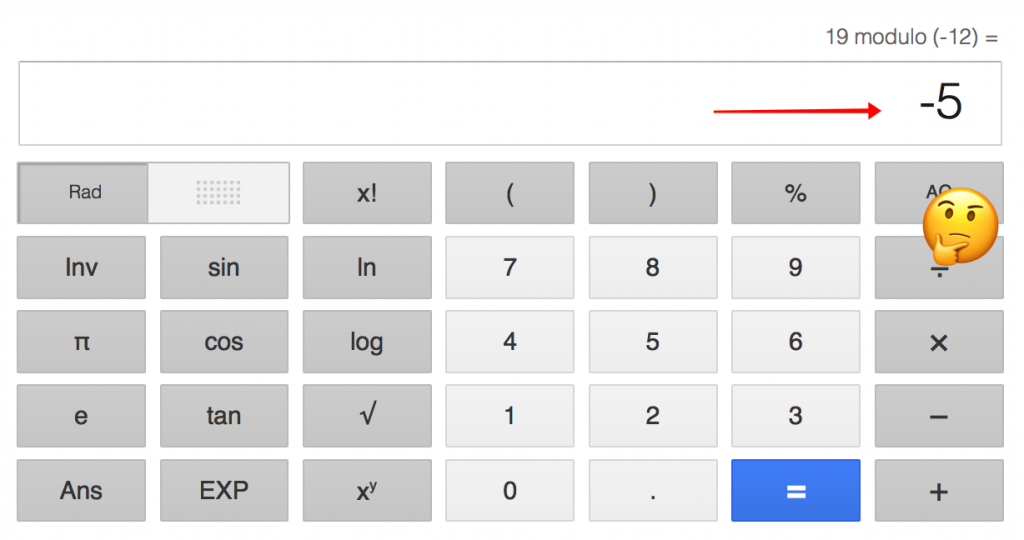
Ruby est d'accord avec Google:
 Au nom de Dijkstra, que se passe-t-il ici?
Au nom de Dijkstra, que se passe-t-il ici?Il y a quelques heures
Pour répondre à la question, vous devez comprendre la différence entre le
reste et le
modulo .
Les programmeurs combinent ces opérations , mais ne devraient pas le faire, car elles ne donnent le même résultat que si le diviseur (dans notre cas 12) est positif. Vous pouvez facilement envoyer des bugs en production si le diviseur est négatif.
Mais pourquoi y a-t-il une différence? Considérez le diviseur positif
19 mod 12 sur l'horloge:
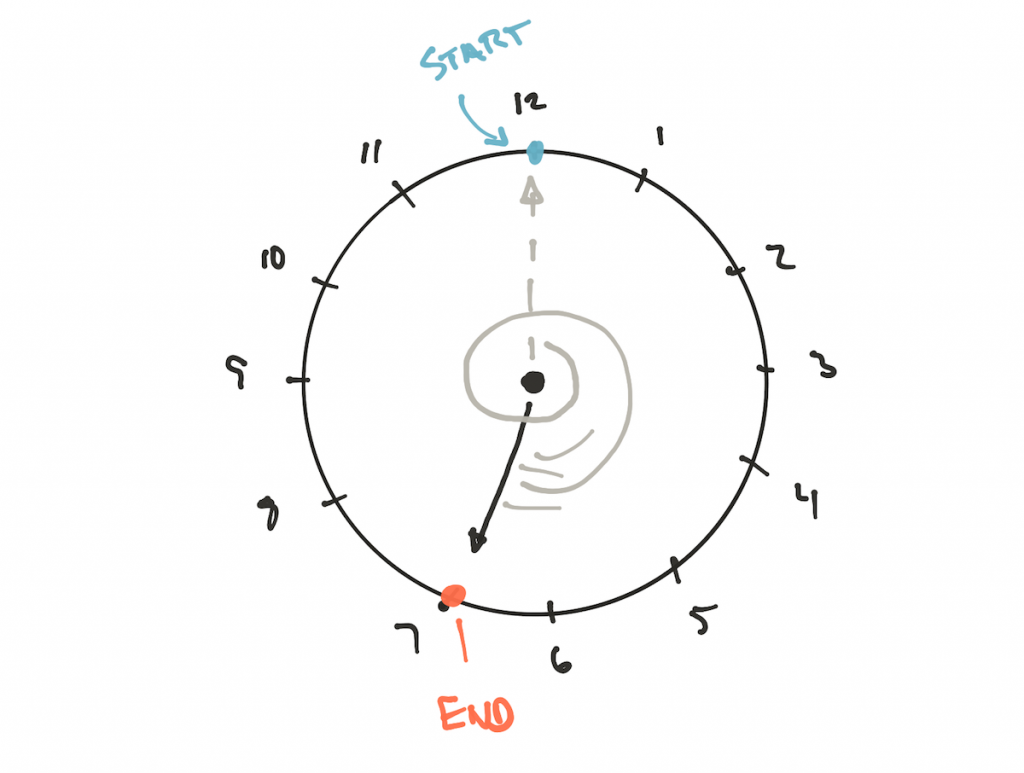
Résultat final 7. Nous le savons et nous pouvons le prouver mathématiquement. Mais qu'en est-il du
19 mod -12 ?
Ici, vous devez utiliser d'autres montres :
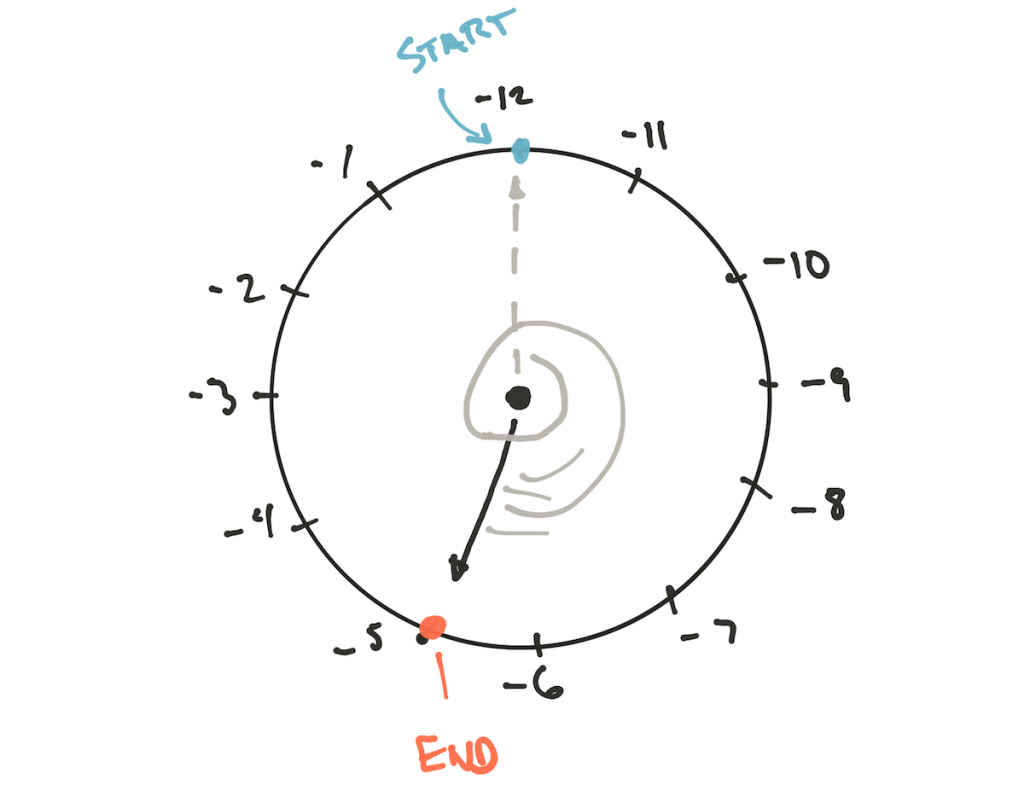
Le module est -12, et nous ne pouvons pas l'ignorer ou le changer en multipliant par -1, car l'arithmétique modulaire ne fonctionne pas de cette façon. La seule façon de calculer correctement le résultat est de réorganiser les marques sur l'horloge afin que nous passions de -12 ou tournions l'horloge dans le sens antihoraire, ce qui donne le même résultat.
Pourquoi ne pas commencer les balises avec -1, passer à -2, etc.?
Parce que dans ce cas, nous reculerons et réduirons constamment le résultat jusqu'à ce que nous atteignions -12, et à ce moment nous ferons un saut +12, et le modulo ne fonctionne pas comme ça.
C'est une chose célèbre.
Avant de me traiter de fou et de commencer à googler un sujet:
c'est un fait bien connu . En fait, le MDN (Mozilla Developer Network) est même allé jusqu'à appeler
% l'opération restante, pas modulo:
L'opérateur restant renvoie le reste de la division d'un opérande par un autre. Il accepte toujours le signe du dividende .
Voici ce qu'Eric Lippert, l'un des dieux C #,
dit à propos du modulo en C # :
Cependant, ce n'est pas du tout ce que fait réellement l'opérateur% en C #. L'opérateur% n'est pas un opérateur de module canonique, c'est un opérateur de reste.
Et votre langue?
Et alors?
Je peux comprendre si vous avez lu jusqu'ici, et maintenant vous gratter la tête et vous demander si cela vaut la peine de vous inquiéter. Je pense que cela coûte pour deux raisons:
- Je peux imaginer comment cette question me surprendra lors d'une interview.
- Je peux imaginer comment celui-ci entre en production, et les développeurs découvriront pendant plusieurs heures pourquoi les mathématiques ne fonctionnent pas.
C'est aussi un fait amusant au cas où votre ami programmeur pédant viendrait.