Une méthode universelle de tri des informations complexes a été découverte

En ouvrant votre café, vous souhaitez connaître la réponse à la question suivante: "où est l'autre café le plus proche de ce point?" Ces informations vous aideraient à mieux comprendre vos concurrents.

Ceci est un exemple du problème de recherche du « plus proche voisin », qui est largement étudié en informatique. Étant donné un ensemble d'informations et un nouveau point, et vous devez trouver à quel point des points existants il sera le plus proche? Une telle question se pose dans de nombreuses situations quotidiennes dans des domaines tels que la recherche sur le génome, la recherche d'images et les recommandations Spotify.

Mais, contrairement à l'exemple du café, les questions sur le plus proche voisin sont souvent très compliquées. Au cours des dernières décennies, les plus grands esprits des informaticiens ont cherché à trouver les meilleurs moyens de résoudre ce problème. En particulier, ils ont essayé de faire face aux complications résultant du fait que dans différents ensembles de données, il peut y avoir des définitions très différentes de la «proximité» des points les uns par rapport aux autres.

Et maintenant, une équipe d'informaticiens a trouvé une toute nouvelle façon de résoudre le problème de trouver le plus proche voisin. Dans une paire d' articles, cinq scientifiques ont décrit en détail la première méthode généralisée pour résoudre le problème de trouver le plus proche voisin pour des données complexes.

«Il s'agit du premier résultat couvrant un large éventail d'espaces utilisant une seule technique algorithmique», a déclaré Peter Indik , spécialiste informatique au Massachusetts Institute of Technology, une figure influente dans le domaine des développements liés à cette tâche.

Différence de distance

Nous sommes tellement attachés à la seule façon de déterminer la distance qu'il est facile de perdre de vue la possibilité d'autres voies. Habituellement, nous mesurons la distance comme euclidienne - comme une ligne droite entre deux points. Cependant, il existe des situations dans lesquelles d'autres définitions ont plus de sens. Par exemple, la distance de Manhattan vous fait tourner à 90 degrés, comme si vous vous déplaciez le long d'un réseau rectangulaire de routes. Pour mesurer une distance qui pourrait être de 5 kilomètres en ligne droite, vous devrez peut-être traverser la ville sur 3 km dans un sens puis sur 4 kilomètres de plus dans l'autre.

Il est également possible de parler de distances non dans un sens géographique. Quelle est la distance entre deux personnes dans un réseau social, ou deux films, ou deux génomes? Dans ces exemples, la distance indique le degré de similitude.

Il existe des dizaines de métriques de distance, chacune étant adaptée à une tâche spécifique. Prenons, par exemple, deux génomes. Les biologistes les comparent en utilisant la " distance Levenshtein " ou la distance d'édition. La distance d'édition entre deux séquences du génome est le nombre d'additions, de suppressions, d'insertions et de substitutions nécessaires pour transformer l'une d'elles en une autre.

Modifier la distance et la distance euclidienne sont deux concepts différents de distance, et il est impossible de les réduire l'un à l'autre. Cette incompatibilité existe pour de nombreuses paires de métriques de distance et constitue un obstacle pour les informaticiens qui tentent de développer des algorithmes pour trouver le plus proche voisin. Cela signifie qu'un algorithme qui fonctionne pour un type de distance ne fonctionnera pas pour un autre - plus précisément, il en était ainsi jusqu'à présent, jusqu'à ce qu'un nouveau type de recherche apparaisse.


Alexander Andoni

Cercle carré

L'approche standard pour trouver le plus proche voisin consiste à diviser les données existantes en sous-groupes. Si, par exemple, vos données décrivent l'emplacement des vaches dans le pâturage, alors vous pouvez les entourer chacune d'un cercle. Ensuite, nous mettons une nouvelle vache sur le pré et posons la question: dans quels cercles appartient-elle? Il est pratiquement garanti que le plus proche voisin de la nouvelle vache sera dans le même cercle.

Répétez ensuite le processus. Divisez les cercles en sous-cercles, divisez davantage ces cellules, etc. En conséquence, il y a une cellule avec seulement deux points: l'existant et le nouveau. Ce point existant sera votre plus proche voisin.


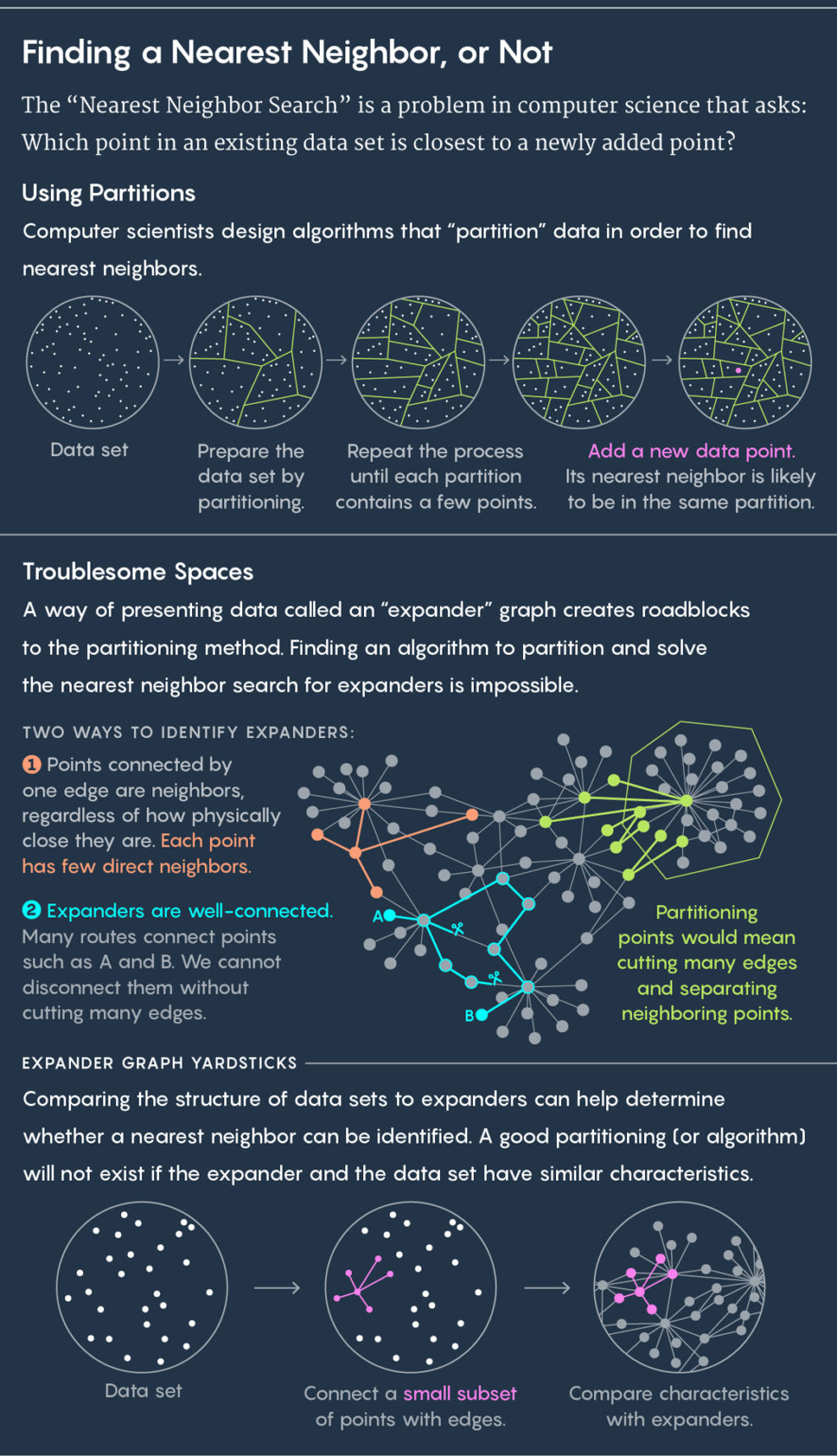Ci-dessus, la division des données en cellules. Voici l'utilisation du graphique d'extension.

Les algorithmes dessinent les cellules, les bons algorithmes les dessinent rapidement et bien - c'est-à-dire qu'il n'y a pas de situation dans laquelle une nouvelle vache tombe dans un cercle et son voisin le plus proche se retrouve dans un autre cercle. «Nous voulons que les points proches de ces cellules apparaissent plus souvent dans le même lecteur les uns avec les autres, et que les points distants soient rares», a déclaré Ilya Razenshtein , spécialiste en informatique chez Microsoft Research, co-auteur du nouveau travail, qui a également impliqué Alexander Andoni de l'Université Columbia. , Assaf Naor de Princeton, Alexander Nikolov de l'Université de Toronto et Eric Weingarten de l'Université Columbia.

Pendant de nombreuses années, les informaticiens ont mis au point divers algorithmes pour dessiner de telles cellules. Pour les petites données - comme lorsqu'un point est déterminé par un petit nombre de valeurs, par exemple, l'emplacement d'une vache dans un pâturage - les algorithmes créent ce que l'on appelle Des « diagrammes de Voronoi » qui répondent avec précision à la question concernant le plus proche voisin.

Pour les données multidimensionnelles, dans lesquelles un point peut être déterminé par des centaines ou des milliers de valeurs, les diagrammes de Voronoi nécessitent trop de puissance de calcul. Au lieu de cela, les programmeurs dessinent des cellules en utilisant un « hachage localement sensible » , décrit pour la première fois par Indik et Rajiv Motwani en 1998. Les algorithmes LF dessinent des cellules de manière aléatoire. Par conséquent, ils travaillent plus rapidement, mais avec moins de précision - au lieu de trouver le voisin le plus proche exact, ils garantissent qu'un point n'est pas situé à plus d'une distance donnée du vrai voisin le plus proche. Cela peut être imaginé comme une recommandation de film Netflix, ce qui n'est pas parfait, mais assez bon.

Depuis la fin des années 1990, les informaticiens ont mis au point des algorithmes LF qui fournissent des solutions approximatives pour la tâche de trouver le plus proche voisin pour des métriques de distance données. Les algorithmes étaient très spécialisés et l'algorithme développé pour une métrique de distance ne pouvait pas être utilisé pour une autre.

«Vous pouvez trouver un algorithme très efficace pour la distance euclidienne ou Manhattan, pour certains cas spécifiques. Mais nous n'avions pas d'algorithme qui fonctionnait sur une grande classe de distances », a déclaré Indik.

Étant donné que les algorithmes fonctionnant avec une métrique ne pouvaient pas être utilisés pour une autre, les programmeurs ont proposé une stratégie de contournement. Grâce à un processus appelé «intégration», ils ont imposé une métrique, pour laquelle ils n'avaient pas un bon algorithme, sur la métrique pour laquelle il était. Cependant, la correspondance des mesures était généralement inexacte - quelque chose comme une cheville carrée dans un trou rond. Dans certains cas, l'intégration n'a pas fonctionné du tout. Il fallait trouver un moyen universel de répondre à la question du plus proche voisin.


Ilya Razenshtein

Résultat inattendu

Dans un nouveau travail, les scientifiques ont abandonné la recherche d'algorithmes spéciaux. Au lieu de cela, ils ont posé une question plus large: qu'est-ce qui empêche le développement d'un algorithme sur une certaine métrique de distance?

Ils ont décidé que la situation désagréable associée au graphique en expansion ou à l' expandeur était à blâmer. Un expandeur est un type spécial de graphique, un ensemble de points reliés par des arêtes. Les graphiques ont leur propre métrique de distance. La distance entre deux points du graphique est le nombre minimum de lignes nécessaires pour passer d'un point à un autre. Vous pouvez imaginer un graphique représentant les connexions entre les personnes dans les réseaux sociaux, puis la distance entre les personnes sera égale au nombre de connexions les séparant. Si, par exemple, Julian Moore a un ami qui a un ami dont Kevin Bacon est l'ami, alors la distance entre Moore et Bacon est de trois.

Un expandeur est un type spécial de graphe qui possède à première vue deux propriétés conflictuelles. Il a une connectivité élevée, c'est-à-dire que deux points ne peuvent pas être déconnectés sans couper plusieurs bords. Dans le même temps, la plupart des points sont connectés à un très petit nombre d'autres. Pour cette raison, la plupart des points sont éloignés les uns des autres.

Une combinaison unique de ces propriétés - une bonne connectivité et un petit nombre d'arêtes - conduit au fait que sur les expandeurs, il est impossible de rechercher rapidement le voisin le plus proche. Toute tentative de le diviser en cellules séparera les points proches les uns des autres.

"Toute façon de couper l'expanseur en deux parties nécessite de couper plusieurs nervures, ce qui divise de nombreux sommets étroitement espacés", a déclaré Weingarten, co-auteur de l'ouvrage.

À l'été 2016, Andoni, Nyokolov, Rasenstein et Vanguarten savaient que pour les expanseurs, on ne pouvait pas trouver un bon algorithme pour trouver le plus proche voisin. Mais ils voulaient prouver qu'il est impossible de construire de tels algorithmes pour de nombreuses autres métriques de distance - les métriques, lors de la recherche de bons algorithmes pour lesquels les informaticiens sont au point mort.

Pour trouver des preuves de l'impossibilité de tels algorithmes, ils devaient trouver un moyen d'incorporer la métrique d'expansion dans d'autres métriques de distance. Avec cette méthode, ils pourraient déterminer que d'autres mesures ont des propriétés similaires aux propriétés de l'expandeur, ce qui les empêche de faire de bons algorithmes.


Eric Weingarten

Quatre informaticiens se sont rendus à Assaf Naoru, un mathématicien de l'Université de Princeton, dont les travaux antérieurs étaient bien adaptés au sujet des expanseurs. Ils lui ont demandé de l'aider à prouver que les expandeurs peuvent être intégrés dans différents types de mesures. Naor revint rapidement avec une réponse - mais pas celle qu'ils attendaient de lui.

"Nous avons demandé à Assaf de nous aider avec cette déclaration, et il a prouvé le contraire", a déclaré Andoni.

Naor a prouvé que les expanseurs ne rentrent pas dans une grande classe de métriques de distance appelées « espaces normés » (qui inclut également des métriques telles que les espaces euclidiens et Manhattan). Sur la base des preuves de Naor, les scientifiques ont suivi la chaîne logique suivante: si les expandeurs ne correspondent pas à la métrique de distance, alors il devrait y avoir un bon moyen de les diviser en cellules (car, comme ils l'ont prouvé, les propriétés des expandeurs sont le seul obstacle à cela). Par conséquent, il doit y avoir un bon algorithme pour trouver le plus proche voisin - même si personne ne l'a encore trouvé.

Cinq chercheurs ont publié leurs résultats dans un document qu'ils ont terminé en novembre et téléchargé en avril. Il a été suivi d'un deuxième ouvrage, qu'ils ont achevé cette année et publié en août. Dans ce document, ils ont utilisé les informations obtenues lors de l'écriture du premier travail pour trouver un algorithme rapide pour trouver le plus proche voisin pour les espaces normés.

"Le premier travail a démontré l'existence d'un moyen de diviser la métrique en deux parties, mais il n'y avait pas de recette pour le faire rapidement", a déclaré Weingarten. "Dans le deuxième travail, nous soutenons qu'il existe un moyen de séparer les points, et en plus, que cette séparation peut être effectuée en utilisant des algorithmes rapides."

De nouveaux travaux généralisent pour la première fois la recherche du plus proche voisin dans les données multidimensionnelles. Au lieu de développer des algorithmes spécialisés pour des mesures spécifiques, les programmeurs ont une approche universelle pour trouver des algorithmes.

"Il s'agit d'une méthode ordonnée pour développer des algorithmes pour trouver le voisin le plus proche à l'une des mesures de distance dont vous avez besoin", a déclaré Weingarten.