
Maintenant, tout le monde parle beaucoup de l'intelligence artificielle et de son application dans tous les domaines de l'entreprise. Cependant, il existe certains domaines où, depuis l'Antiquité, un type de modèle a dominé, la soi-disant «boîte blanche» - la régression logistique. L'un de ces domaines est la notation du crédit bancaire.
Il y a plusieurs raisons à cela:
- Les coefficients de régression peuvent être facilement expliqués, contrairement aux boîtes noires comme le boosting, qui peuvent inclure plus de 500 variables
- L'apprentissage automatique n'est toujours pas approuvé par la direction en raison de la difficulté d'interprétation des modèles
- Il existe des exigences non écrites du régulateur pour l'interprétabilité des modèles: à tout moment, par exemple, la Banque centrale peut demander une explication - pourquoi un prêt à l'emprunteur a été refusé
- Les entreprises utilisent des programmes externes d'exploration de données (par exemple, mineur rapide, SAS Enterprise Miner, STATISTICA ou tout autre package) qui vous permettent d'apprendre rapidement à construire des modèles, même sans compétences en programmation
Ces raisons font qu'il est presque impossible d'utiliser des modèles complexes d'apprentissage automatique dans certains domaines, il est donc important de pouvoir «tirer le maximum» d'une simple régression logistique, qui est facile à expliquer et à interpréter.
Dans cet article, nous expliquerons comment, lors de la création du scoring, nous avons abandonné les packages d'exploration de données externes au profit de solutions open source sous la forme de Python, augmenté plusieurs fois la vitesse de développement et amélioré la qualité de tous les modèles.
Processus de notation
Le processus classique de construction de modèles de notation sur la régression ressemble à ceci:
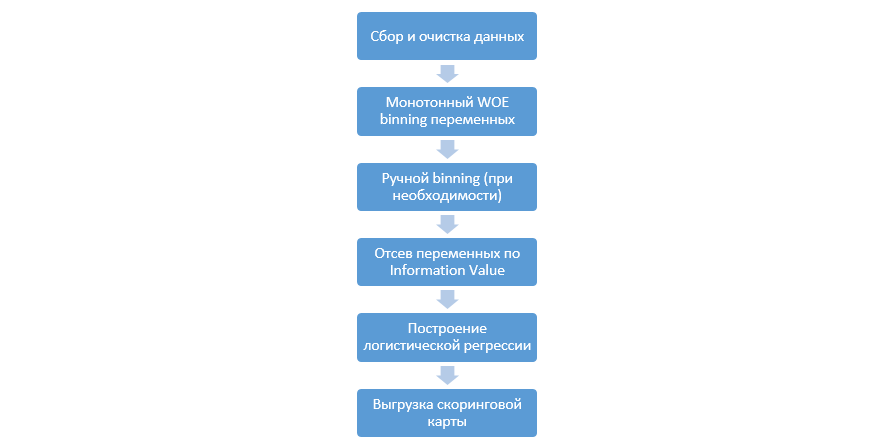
Elle peut varier d'une entreprise à l'autre, mais les principales étapes restent constantes. Nous devons toujours effectuer un regroupement de variables (contrairement au paradigme d'apprentissage automatique, où dans la plupart des cas, seul un codage catégoriel est nécessaire), leur filtrage par valeur d'information (IV) et le téléchargement manuel de tous les coefficients et bacs pour une intégration ultérieure dans DSL.
Cette approche de la création de cartes de notation a bien fonctionné dans les années 90, mais les technologies des packages classiques d'exploration de données sont très dépassées et ne permettent pas l'utilisation de nouvelles techniques, telles que, par exemple, la régularisation L2 en régression, ce qui peut améliorer considérablement la qualité des modèles.
À un moment donné, en tant qu'étude, nous avons décidé de reproduire toutes les étapes que les analystes effectuent lors de la création du score, de les compléter avec les connaissances des Data Scientists et d'automatiser autant que possible l'ensemble du processus.
Amélioration de Python
En tant qu'outil de développement, nous avons choisi Python pour sa simplicité et ses bonnes bibliothèques, et avons commencé à jouer toutes les étapes dans l'ordre.
La première étape consiste à collecter des données et à générer des variables - cette étape est une partie importante du travail des analystes.
En Python, vous pouvez charger les données collectées à partir de la base de données à l'aide de pymysql.
Code à télécharger depuis la base de donnéesdef con(): conn = pymysql.connect( host='10.100.10.100', port=3306, user='******* ', password='*****', db='mysql') return conn; df = pd.read_sql(''' SELECT * FROM idf_ru.data_for_scoring ''', con=con())
Ensuite, nous remplaçons les valeurs rares et manquantes par une catégorie distincte pour empêcher le suraménagement, sélectionnons la cible, supprimons les colonnes supplémentaires et divisons par train et test.
Préparation des données def filling(df): cat_vars = df.select_dtypes(include=[object]).columns num_vars = df.select_dtypes(include=[np.number]).columns df[cat_vars] = df[cat_vars].fillna('_MISSING_') df[num_vars] = df[num_vars].fillna(np.nan) return df def replace_not_frequent(df, cols, perc_min=5, value_to_replace = "_ELSE_"): else_df = pd.DataFrame(columns=['var', 'list']) for i in cols: if i != 'date_requested' and i != 'credit_id': t = df[i].value_counts(normalize=True) q = list(t[t.values < perc_min/100].index) if q: else_df = else_df.append(pd.DataFrame([[i, q]], columns=['var', 'list'])) df.loc[df[i].value_counts(normalize=True)[df[i]].values < perc_min/100, i] =value_to_replace else_df = else_df.set_index('var') return df, else_df cat_vars = df.select_dtypes(include=[object]).columns df = filling(df) df, else_df = replace_not_frequent_2(df, cat_vars) df.drop(['credit_id', 'target_value', 'bor_credit_id', 'bchg_credit_id', 'last_credit_id', 'bcacr_credit_id', 'bor_bonuses_got' ], axis=1, inplace=True) df_train, df_test, y_train, y_test = train_test_split(df, y, test_size=0.33, stratify=df.y, random_state=42)
Commence maintenant l'étape la plus importante de la notation pour la régression - vous devez écrire le regroupement WOE pour les variables numériques et catégorielles. Dans le domaine public, nous n'avons pas trouvé de bonnes et adaptées options pour nous et avons décidé de nous écrire.
Cet article de 2017 a été pris comme base du binning numérique, ainsi que
cela , catégorique, ont-ils écrit eux-mêmes à partir de zéro. Les résultats étaient impressionnants (Gini sur le test a augmenté de 3 à 5 par rapport aux algorithmes de binning des programmes externes d'exploration de données).
Après cela, vous pouvez regarder les graphiques ou les tableaux (que nous écrivons ensuite en excel) comment les variables sont divisées en groupes et vérifier la monotonie:
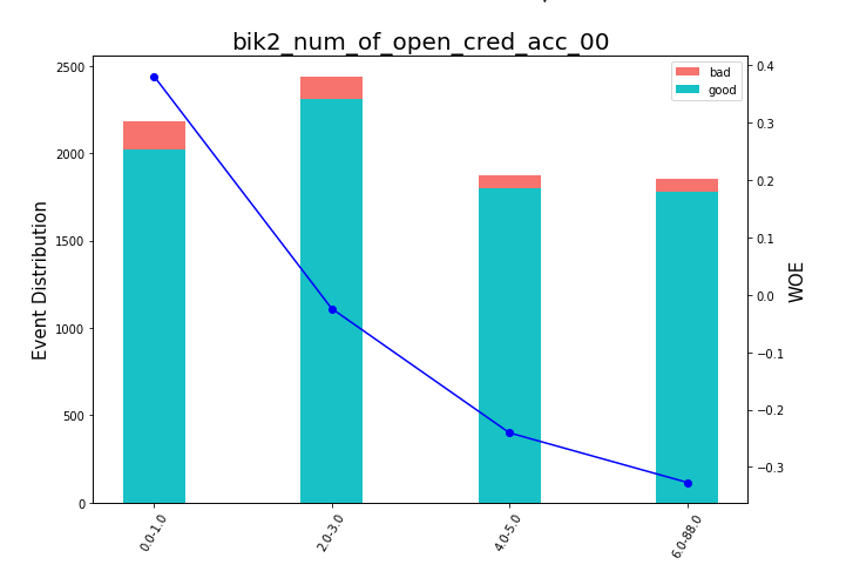
Rendu des graphiques Bean def plot_bin(ev, for_excel=False): ind = np.arange(len(ev.index)) width = 0.35 fig, ax1 = plt.subplots(figsize=(10, 7)) ax2 = ax1.twinx() p1 = ax1.bar(ind, ev['NONEVENT'], width, color=(24/254, 192/254, 196/254)) p2 = ax1.bar(ind, ev['EVENT'], width, bottom=ev['NONEVENT'], color=(246/254, 115/254, 109/254)) ax1.set_ylabel('Event Distribution', fontsize=15) ax2.set_ylabel('WOE', fontsize=15) plt.title(list(ev.VAR_NAME)[0], fontsize=20) ax2.plot(ind, ev['WOE'], marker='o', color='blue')
Une fonction de binning manuel a été écrite séparément, ce qui est utile, par exemple, dans le cas de la variable «version OS», où tous les téléphones Android et iOS ont été regroupés manuellement.
Fonction de binning manuel def adjust_binning(df, bins_dict): for i in range(len(bins_dict)): key = list(bins_dict.keys())[i] if type(list(bins_dict.values())[i])==dict: df[key] = df[key].map(list(bins_dict.values())[i]) else:
L'étape suivante est la sélection des variables par valeur d'information. La valeur par défaut est coupée 0,1 (toutes les variables ci-dessous n'ont pas un bon pouvoir prédictif).
Après cela, un contrôle de corrélation a été effectué. Des deux variables corrélatives, vous devez supprimer celle qui a le moins d'IV. Le retrait de coupure a été effectué 0,75.
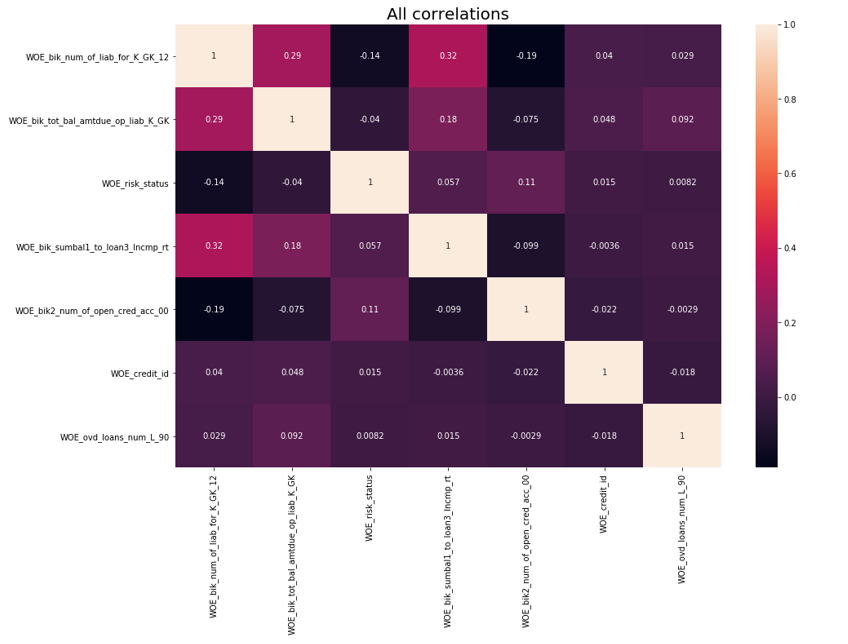
Suppression de la corrélation def delete_correlated_features(df, cut_off=0.75, exclude = []):
En plus de la sélection par IV, nous avons ajouté une recherche récursive du nombre optimal de variables par la méthode
RFE de sklearn.
Comme nous le voyons dans le graphique, après 13 variables, la qualité ne change pas, ce qui signifie que les variables supplémentaires peuvent être supprimées. Pour la régression, plus de 15 variables de notation sont considérées comme de mauvaise forme, qui dans la plupart des cas sont corrigées à l'aide de RFE.
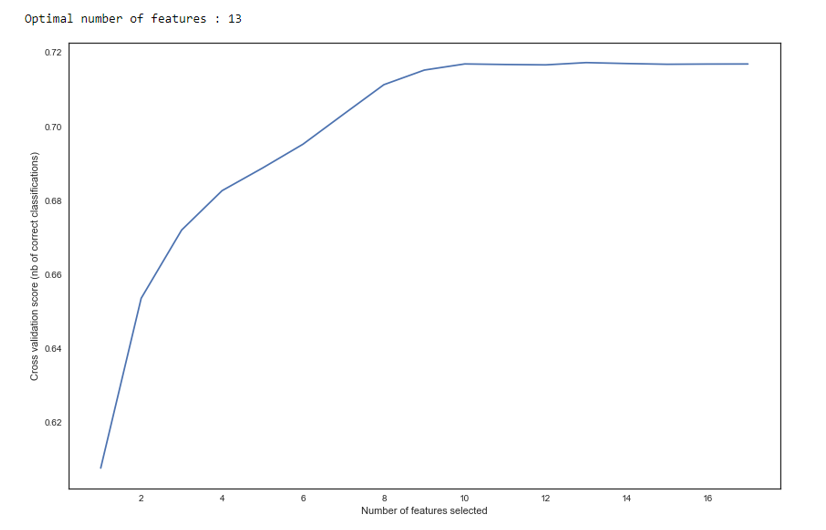
RFE def RFE_feature_selection(clf_lr, X, y): rfecv = RFECV(estimator=clf_lr, step=1, cv=StratifiedKFold(5), verbose=0, scoring='roc_auc') rfecv.fit(X, y) print("Optimal number of features : %d" % rfecv.n_features_)
Ensuite, une régression a été construite et ses paramètres ont été évalués sur la validation croisée et l'échantillonnage d'essai. Habituellement, tout le monde regarde le coefficient de Gini (un bon article à son sujet
ici ).
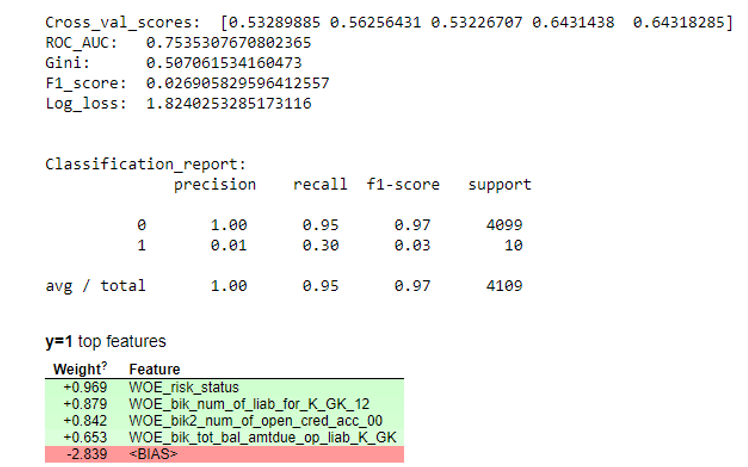
Résultats de la simulation def plot_score(clf, X_test, y_test, feat_to_show=30, is_normalize=False, cut_off=0.5):
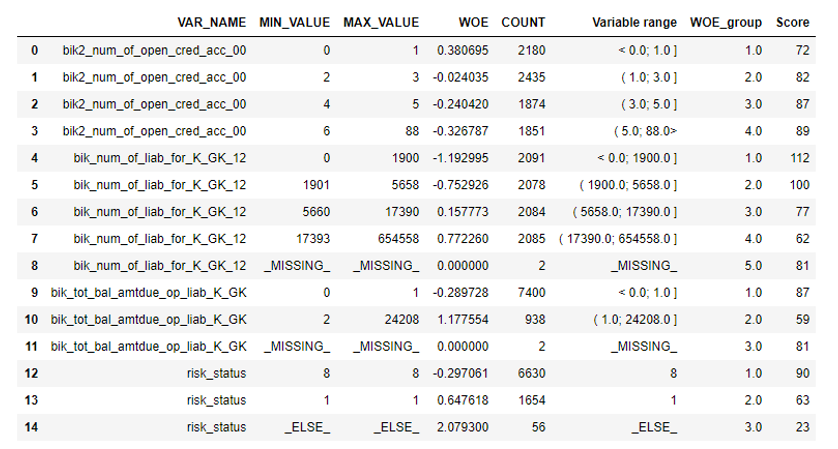
Lorsque nous nous assurons que la qualité du modèle nous convient, il est nécessaire d'écrire tous les résultats (coefficients de régression, groupes de casiers, graphiques et variables de stabilité de Gini, etc.) dans Excel. Pour cela, il est pratique d'utiliser xlsxwriter, qui peut fonctionner avec des données et des images.
Exemples de feuilles Excel:
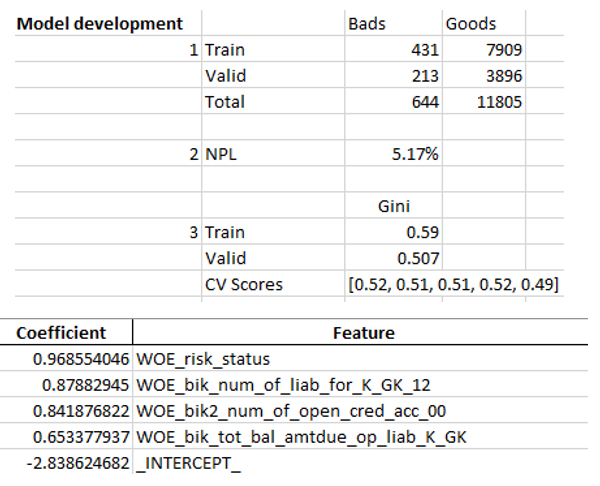
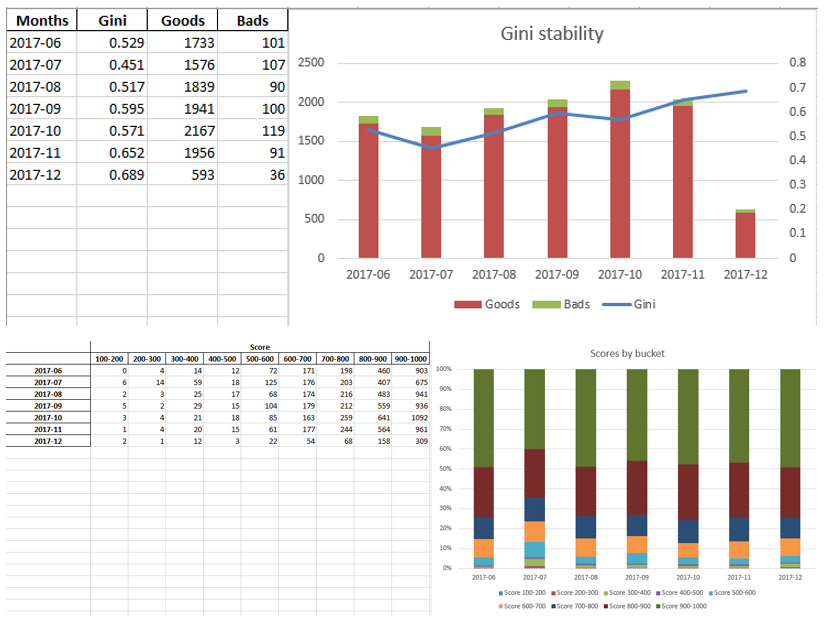
À la fin, l'excellence finale est à nouveau regardée par la direction, après quoi elle est donnée à l'informatique pour l'intégration du modèle dans la production.
Résumé
Comme nous l'avons vu, presque toutes les étapes de la notation peuvent être automatisées afin que les analystes n'aient pas besoin de compétences en programmation pour créer des modèles. Dans notre cas, après avoir créé ce framework, l'analyste n'a plus qu'à collecter des données et spécifier plusieurs paramètres (indiquer la variable cible, les colonnes à supprimer, le nombre minimum de cases, le coefficient de coupure pour la corrélation des variables, etc.), après quoi vous pouvez exécuter le script en python, qui va construire le modèle et produire Excel avec les résultats souhaités.
Bien sûr, il est parfois nécessaire de corriger le code pour les besoins d'un projet particulier, et vous ne pouvez pas le faire avec un seul bouton pour exécuter le script pendant la modélisation, mais même maintenant, nous voyons une meilleure qualité que les packages d'exploration de données utilisés sur le marché grâce à des techniques telles que le binning optimal et monotone, la vérification de la corrélation , RFE, version régularisée de régression, etc.
Ainsi, grâce à l'utilisation de Python, nous avons considérablement réduit le temps de développement des cartes de notation, ainsi que les coûts de main-d'œuvre des analystes.