Dans les parties précédentes ...

0. Détection automatique de la topologie du réseau et commutateurs non gérés. Mission impossible? (+ classique Habrahabr UserCSS )

1. Premières étapes dans OMNeT ++ et INET [tutoriel]

Q: Qu'avons-nous?
R: Statistiques collectées auprès des hôtes.

Q: Que voulons-nous obtenir?
R: Topologie du réseau! Plus précisément, vous devez créer la chaîne de pairs (hôtes) appropriée pour RingSync .

Nous devons trouver un algorithme qui transforme d'abord les statistiques en topologie de réseau, puis en chaîne de pairs. Jusqu'à présent, l'algorithme ressemble à ceci:

 –-[**]-->   --[**]-->

Si vous avez aimé lire la «Partie 1» sur les pages GitHub , voici un lien vers cette partie sur les pages GitHub.

Avertissement : Vous trouverez ci-dessous les mêmes artefacts Habr-parser que j'ai avertis dans la "Partie 1" .

Toute technologie suffisamment avancée est indiscernable de la magie. - Arthur C. Clarke

Remarque : plus loin au lieu de « –-[**]--> », j'utiliserai « –-[???]--> ».

Les statistiques collectées nous montrent sur quels hôtes la vitesse de réception du trafic de diffusion a chuté. Par exemple, regardez le résultat de l'itération zéro dans le réseau "N2_2" (" Network " de l'article précédent "LLTR Part 1"):

 {300,164,164},

2 États hôtes sont clairement visibles ici:

vitesse normale (valeur « 300 ») - aucune réaction ;
la vitesse a chuté (valeur " 164 ") - il y a une réaction .

À quoi je veux en venir? À la binarisation! Si nous codons l' absence de réaction comme 0 et la présence d'une réaction comme 1 , alors nous pouvons mettre toutes les réponses des hôtes en une seule itération dans une variable ( 32 - 512 bits [ AVX - 512 ]). En plus d'économiser de la mémoire (et de l'espace dépensé dans les caches), cela augmentera la vitesse de traitement - toutes les réponses de l'hôte d'une itération particulière ( SIMD ) seront traitées simultanément dans une instruction.

Remarque : car l'utilisation de LLTR Basic pour un grand nombre d'hôtes coûte très cher ( voir le début de la section «LLTR Part 0 :: LLTR Advanced» ), puis tout tient dans des registres 64 bits x86-64.

Remarque : Dans le texte du lien vers la section située dans un autre article (une autre partie), j'ajouterai le numéro de pièce au format: « LLTR Part # :: ‹ section name › ». Et dans le " title " du lien, j'écrirai le nom de la partie, par exemple, pour "LLTR Part 0 ::", "Détecter automatiquement la topologie du réseau et les commutateurs non gérés apparaîtront." Mission impossible? "

Prenons le même exemple d'itération zéro et voyons à quoi cela ressemblera après la binarisation:

 {300,164,164} --[]--> 011

Très compact, mais j'aimerais que « 1 » (la présence d'une réaction ) attire immédiatement mon attention lors de l'affichage d'une liste de toutes les itérations. Maintenant, " 1 " ne se distingue pas du fond " 0 " (fausses données, pour un exemple visuel ):

 0101011010110 1100010110010 0101101010111 0100010110100

Pour mettre en évidence « 1 », j'introduis la notation:

« 1 » signifie 1 - il y a une réaction ;
" . ”Signifie 0 - aucune réaction .

Regardons à nouveau les «fausses données»:

 .1.1.11.1.11. 11...1.11..1. .1.11.1.1.111 .1...1.11.1..

Tellement mieux (à mon humble avis ).

Pour l'instant, l'algorithme ressemble à ceci:

  –-[]-->   --[???]-->   --[???]-->

Nous laissons les détails de la binarisation à la fin de l'article et nous concentrons sur le reste de l'algorithme.

Il est plus facile de créer un algorithme basé sur des données d'entrée / entrée spécifiques (cas particuliers, conditions aux limites; tests en termes de TDD ). Dans notre cas, les données initiales dépendent de la topologie du réseau, vous devez donc trouver un réseau qui serait à la fois petit et contenant en même temps différents schémas de connexion de commutateur ( étoile , connexion série ). Il sera peut-être possible d'y inclure quelque chose de spécial ... En général, l'imagination a dessiné un tel réseau (la notation des éléments est similaire à la notation utilisée à la fin de la section " LLTR Part 0 :: Topologie:" connexion série des commutateurs " "):

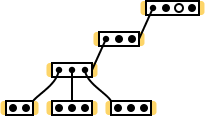
Remarque : en regardant ce réseau, la question "est-il possible d'effectuer une analyse complète dans cette topologie si l'un des commutateurs ..." (vers la fin de la section " LLTR Part 0 :: Topologie:" connexion série des commutateurs " "), et vous remarquez qu'aucun hôte n'est directement connecté à l'un des commutateurs. De plus, il n'y a pas de problème, car 3 autres commutateurs sont connectés à ce commutateur (j'ai compté uniquement les commutateurs connectés «par le bas», sans considérer qu'il est connecté à un autre commutateur «par le haut»), chacun ayant des hôtes.

Cependant, dans ce diagramme, il y a quelques détails supplémentaires (distrayants). Je vais le nettoyer en supprimant:

hôte de diffusion (il n'est pas dans l'entrée / les statistiques);
ports reliant les commutateurs entre eux.

Graphique: réseau hybride LLTR (effacer)

Ici, le commutateur «sans hôtes» est immédiatement visible. De plus, j'ai disposé tous les commutateurs de manière à ce que les hôtes ne se chevauchent pas verticalement. Cela sera utile si, à l'avenir, je souhaite afficher les «réactions de l'hôte» non pas sous la forme d'une entrée de texte « .....1...... », mais sous la forme d'un diagramme (il n'y a qu'un seul hôte sur une verticale):

Graphique: réseau hybride LLTR (clair), explication de la désignation des "réponses de l'hôte"

Imaginez maintenant les statistiques que nous obtenons à la fin de toutes les itérations de l'analyse de ce réseau. Il y a 12 hôtes dans le réseau (hors hôte de diffusion), par conséquent, nous aurons des données sur 132 itérations. Cependant, tous les résultats de l'itération ne nous seront pas utiles, par exemple, ils seront inutiles:

réactions simples (comme dans l'exemple ci-dessus - " .....1...... "; LLTR Part 0 :: Je me demande quelles pourraient être les options pour la première itération?> Option 4: "unicast in sw" );
les doubles (résultats répétés), par exemple, " .....111.... " se produiront environ 15 fois ( 3 × (12 - 3− (2 + 2)) ; "environ", parce que je ne J'ai créé un modèle de ce réseau dans OMNeT ++ , et n'ai pas exécuté la simulation, je n'ai mené qu'une expérience de pensée dans laquelle je n'ai pas pu prendre en compte certains détails).

Après le nettoyage, sur les 132 résultats d'itération, seuls 5 (réponses de l'hôte) resteront:

 1111111111.. 11111111.... ..111....... .....111.... 11..........

Remarque : pour plus de clarté, j'ai organisé les itérations dans l'ordre, d'un plus grand nombre de « 1 » à un plus petit.

L'algorithme a commencé à ressembler à ceci:

  –-[]-->   --[   ]--[  ]--[???]-->   --[???]-->

réinitialiser le point

J'ai pensé à inclure tout cela dans le spoiler, mais à la fin j'ai réalisé que c'est une partie importante de l'histoire, qu'il vaut mieux ne pas manquer lors de la lecture.

¬ ( Ne sautez pas au cerveau lors de la lecture : Cong

[point de réinitialisation] Dans les 5 résultats d'itération restants, les deux premiers attirent l'attention: le premier comprend le second, et le second comprend les 3 autres inférieurs. Ici, je rappelle le «shadow» de la section « LLTR Part 0 :: Topology:« serial connection of switches » ». Dans la même section, à la fin de chaque itération, nous avons formé (ou n'avons pas formé) de nouveaux clusters sur la base des données qui viennent d'être obtenues. Maintenant, nous devons faire de même.

Mais comment avons-nous formé de nouveaux clusters? En fait, toutes les réactions (non uniques) des hôtes « 1 » de l'itération actuelle étaient le «nouveau cluster», nous n'avions qu'à trouver les intersections («∩»; pas vides «∅») avec les clusters existants afin de supprimer («∖») du plus grand hôtes de cluster inclus dans un cluster plus petit.

Cependant, dans nos actions, il y avait une condition / ramification (si): vous devez déterminer lequel des clusters est le plus grand, puis effectuer une opération simple (A ∖ B) - soustraire le plus petit (B) du plus grand cluster (A). Représentant le tourment d'un CPU avec un long pipeline causé par la nécessité de réinitialiser le pipeline si la prédiction de branche est incorrecte (s'il y a un "bloc de prédiction de branche"), j'ai presque décidé d'utiliser l' “?: " , Mais à ce moment-là ...

Je me tenais sur les toilettes et suspendais l'horloge. Soudain, il a glissé, s'est cogné la tête contre l'évier, et quand je me suis réveillé, j'ai eu une vision, une image dans mon cerveau, une vision de cela - un séparateur de ~~flux d'entraînement de~~ flux ( Retour vers le futur ) :

 // Flux Divider c=a^b; aa=a&c; bb=b&c; cc=a&b;

Et voir immédiatement son travail sur l'exemple des clusters qui se chevauchent (plus précisément, un ensemble (cluster) est strictement inclus " " dans un autre ensemble):

 .....11..... - a ..11111111.. - b ..111..111.. - c=a^b ............ - aa=a&c ..111..111.. - bb=b&c .....11..... - cc=a&b

Clusters disjoints:

 ..111....... - a .......111.. - b ..111..111.. - c=a^b ..111....... - aa=a&c .......111.. - bb=b&c ............ - cc=a&b

Il s'avère que:

« aa » contient des éléments propres à « a »;
en « bb » - unique à « b »;
en « cc » - commun à « a » et « b ».

Un autre exemple avec des grappes qui se croisent («impossible», mais un bon exemple):

 ...1111..... - a .....1111... - b ...11..11... - c=a^b ...11....... - aa=a&c .......11... - bb=b&c .....11..... - cc=a&b

Remarque : ce type de réponse (réaction de l'hôte) ne figure pas dans les données source.

De la même manière, vous pouvez vous débarrasser des prises :

 .....11..... - a .....11..... - b ............ - c=a^b ............ - aa=a&c ............ - bb=b&c .....11..... - cc=a&b

Mais, un peu plus tard ...

La tête cesse de faire mal après avoir atteint l'évier, l'esprit s'éclaircit et des problèmes évidents surgissent ...

En entrée, nous avons 2 variables (résultats d'itération / réactions de l'hôte / clusters / ensembles / ...), mais il y en a déjà 3 en sortie, et au moins l'une d'entre elles sera vide ("∅"). Si vous ne vous débarrassez pas immédiatement de «∅», vous devrez les inclure dans le traitement à l'avenir. Par conséquent, il est préférable de se débarrasser immédiatement de «∅». Mais comment faire? Utilisez la condition / ramification! ... En général, je suis retourné à mon point de départ. De plus, si tout est fait comme décrit ci-dessus, en plus il se débarrasse de «,», alors à la fin nous obtenons de:

 1111111111.. 11111111.... ..111....... .....111.... 11..........

C’est:

 ........11..             -     "............",     ：（ ..111....... .....111.... 11..........

Il est temps de poser la question: "Comment obtenir la topologie du réseau à partir de cela?" Maintenant, ces données peuvent «dire» à quel cluster un hôte particulier appartient (c'est-à-dire à quel commutateur l'hôte est connecté), mais ces données manquent maintenant complètement d'informations sur la topologie des commutateurs (c'est-à-dire, comment sont connectés commutateurs entre eux) - nous avons perdu ces informations lors de la conversion des données. De plus, à quel cluster (commutateur) les 2 hôtes les plus à droite appartiennent-ils? Si nous considérons chaque ligne comme un cluster séparé (ou comme une indication des hôtes connectés à un commutateur particulier), il s'avère que ces 2 hôtes extrêmes ne sont connectés nulle part! De plus, nous avons 6 commutateurs sur le réseau, et il reste 4 lignes, où sont 2 lignes supplémentaires? Nous en avons effacé un (comme l'indique le commentaire ci-dessus), et dans l'autre, il aurait dû y avoir «2 hôtes à l'extrême droite».

[ goto reset point ] Développer cette idée est inutile. Impasse (branche git). Vous devrez revenir à l'étiquette de «point de réinitialisation», en oubliant tout ce qui était après, mais en laissant cette branche pour l'histoire.

Maintenant, afin de ne pas tomber dans une autre "branche morte", vous devez décider de la structure finale (représentation) de la topologie du réseau en mémoire. Autrement dit, avec ce que nous voulons obtenir au moment de la «topologie du réseau»:

  –-[]-->   --[   ]--[  ]--[???]--> <strong> </strong> --[???]-->

Tout d'abord , tous les hôtes doivent être présents:

 <strong>..........11</strong> <-- 1111111111.. 11111111.... ..111....... .....111.... 11..........

Deuxièmement , les parents doivent être indiqués (le cluster parent pour chaque cluster; pour le moment: parent ⊋ enfant ; sur le schéma du réseau, j'ai placé les parents au-dessus des enfants) (les numéros de cluster sont ajoutés à gauche):

 0) ..........11 parent: ? 1) 1111111111.. parent: ? 2) 11111111.... parent: 1 3) ..111....... parent: 2 4) .....111.... parent: 2 5) 11.......... parent: 2

Remarque : si vous remarquez quelque chose d'étrange ici, en comparant le schéma de ce réseau avec ces données, alors vous m'aimez.

Spoiler, il vaut mieux ne pas ouvrir avant d'avoir lu toute la liste

En fait (selon le diagramme), le parent du cluster 1 est le cluster 0, mais alors la condition « parent ⊋ enfant » n'est pas remplie. Peut-être que dans " First " nous avons fait une erreur, et au lieu de " ..........11 " cela valait la peine d'ajouter " 111111111111 "?

Troisièmement , il devrait y avoir un parent «racine» reliant des arbres individuels (c.-à-d. Forêt ) en un seul arbre:

 -1) 111111111111 0) ..........11 parent:-1 1) 1111111111.. parent:-1 2) 11111111.... parent: 1 3) ..111....... parent: 2 4) .....111.... parent: 2 5) 11.......... parent: 2

Quatrièmement , ce serait bien d'avoir des listes d'enfants avec chaque parent:

 -1) 111111111111            children: 0,1 0) ..........11 parent:-1 1) 1111111111.. parent:-1, children: 2 2) 11111111.... parent: 1, children: 3,4,5 3) ..111....... parent: 2 4) .....111.... parent: 2 5) 11.......... parent: 2

Et enfin , il est désormais possible d'exclure les enfants de leurs parents:

 -1) ............            children: 0,1 0) ..........11 parent:-1 1) ........11.. parent:-1, children: 2 2) ............ parent: 1, children: 3,4,5 3) ..111....... parent: 2 4) .....111.... parent: 2 5) 11.......... parent: 2

Maintenant, chaque ligne décrit un cluster, c'est-à-dire pointe vers des hôtes connectés au même commutateur. Cependant, attendez, il y a 6 commutateurs dans notre réseau, et il y a 7 clusters! Il est enfin temps de lire le texte du spoiler ci-dessus " Spoiler, il vaut mieux ne pas ouvrir avant d'avoir lu la liste entière ", et corriger la situation:

 0) ..........11            children: 1 1) ........11.. parent: 0, children: 2 2) ............ parent: 1, children: 3,4,5 3) ..111....... parent: 2 4) .....111.... parent: 2 5) 11.......... parent: 2

Ces données sont précisément la «topologie du réseau» - elles décrivent l'arborescence des commutateurs, et à partir de là, vous pouvez déterminer tous les hôtes connectés à un commutateur particulier.

  –-[]-->   --[   ]--[  ]--[???]--> <strong> </strong> --[???]-->

Reste à comprendre comment amener les données sur ce formulaire. En fait, tout ce que nous avons fait (d'une part, d'autre part, ...) peut être converti en algorithme:

"Premièrement" (après avoir fait des corrections à partir du spoiler, cela devient similaire à l'action "troisième") - ajoutez un cluster "racine" " 111111111111 " ( universel ), y compris (hôtes de tous les arbres de la forêt, hôtes situés sur le même commutateur que l'hôte de diffusion ), c'est-à-dire Il inclut tous les hôtes du réseau;
«Deuxièmement» - rechercher un parent pour chaque cluster ;
«Quatrièmement» - établir une liste d'enfants pour chaque parent ;
«Et enfin» - l' exclusion des enfants de leurs parents .

Vous pouvez maintenant ajouter ces actions à l'algorithme général (légèrement changé l'apparence):

                                               ●  ●                                [] ►                 [   ]                          [  ] ► /                [ "" ] ► /        [    ] [     ]              [   ] ►   ●                                        [???] ►   ●

Vue alternative

 ●      ► [] ▬   ► [   ]                   [  ] ▬ /   ► [ "" ] ▬ / ► [    ]                   [     ]                   [   ] ●   ► [???] ●    ●

Voyons ce qui se passe si vous appliquez cet algorithme à un autre réseau. Je voudrais prendre le réseau Network_ serial et ses résultats de simulation (statistiques) de la section " LLTR Part 1 :: Plus de réseaux avec différentes topologies, en ajoutant de nouveaux réseaux ".

Remarque : Pourquoi ai-je choisi ce réseau particulier? Il est assez volumineux et il existe des failles dans les données collectées (voir la fin du spoiler «Résultats de simulation» pour ce réseau).

C'est parti!

Binarisation

Réactions de l'hôte:

 .111111.. .111111.. .111111.. .111111.. .111111.. .111111.. .......11 .......11 ..1...... ...1111.. ...1111.. ...1111.. ...1111.. .......11 .......11 1........ ...1111.. ...1111.. ...1111.. ...1111.. .......11 .......11 1........ .1....... ....1.... .....11.. .....11.. .......11 .......11 1........ .1....... ..1...... .....11.. .....11.. .......11 .......11 1........ .1....... ..1...... ...1..... ......1.. ......... ......... ......... .1....... ..1...... ...1..... ....1.... ......... ......... ......... .1....... ..1...... ...1..... ....1.... .....1... ........1 1........ .111111.. .111111.. .111111.. .111111.. .111111.. .111111.. 1........ .111111.. .111111.. .111111.. .111111.. .111111.. .111111.. .......1.

Purification à partir de réactions uniques

 .111111.. --> .111111.. .111111.. --> .111111.. .111111.. --> .111111.. .111111.. --> .111111.. .111111.. --> .111111.. .111111.. --> .111111.. .......11 --> .......11 .......11 --> .......11 ..1...... --> ...1111.. --> ...1111.. ...1111.. --> ...1111.. ...1111.. --> ...1111.. ...1111.. --> ...1111.. .......11 --> .......11 .......11 --> .......11 1........ --> ...1111.. --> ...1111.. ...1111.. --> ...1111.. ...1111.. --> ...1111.. ...1111.. --> ...1111.. .......11 --> .......11 .......11 --> .......11 1........ --> .1....... --> ....1.... --> .....11.. --> .....11.. .....11.. --> .....11.. .......11 --> .......11 .......11 --> .......11 1........ --> .1....... --> ..1...... --> .....11.. --> .....11.. .....11.. --> .....11.. .......11 --> .......11 .......11 --> .......11 1........ --> .1....... --> ..1...... --> ...1..... --> ......1.. --> ......... --> ......... ......... --> ......... ......... --> ......... .1....... --> ..1...... --> ...1..... --> ....1.... --> ......... --> ......... ......... --> ......... ......... --> ......... .1....... --> ..1...... --> ...1..... --> ....1.... --> .....1... --> ........1 --> 1........ --> .111111.. --> .111111.. .111111.. --> .111111.. .111111.. --> .111111.. .111111.. --> .111111.. .111111.. --> .111111.. .111111.. --> .111111.. 1........ --> .111111.. --> .111111.. .111111.. --> .111111.. .111111.. --> .111111.. .111111.. --> .111111.. .111111.. --> .111111.. .111111.. --> .111111.. .......1. -->

Nettoyage des doublons (nous obtenons «clusters / forêt»):

 .111111.. .......11 ...1111.. .....11.. .........

De plus, pour plus de commodité , je vais trier par ordre décroissant de la quantité « 1 »:

 .111111.. ...1111.. .....11.. .......11 .........

Remarque : il peut être utile d'inclure le tri dans l'algorithme. Qu'en penses-tu?

Ajout d'un cluster «racine» (on obtient «clusters / arborescence»):

 111111111 .111111.. ...1111.. .....11.. .......11 .........

Il comprend des hôtes de 2 arbres (à gauche " .111111.. " et à droite " .......11 " du réseau) et 1 hôte (" 1........ " situé sur un commutateur avec hôte de diffusion).

Recherche parent pour chaque cluster:

 0) 111111111 1) .111111.. parent: 0 2) ...1111.. parent: 1 3) .....11.. parent: 2 4) .......11 parent: 0 5) ......... parent: 4

Remarque : C'est là que s'est produit l'impact négatif des lacunes dans les données - le 4e cluster est devenu le parent du 5e! En général, tout cluster peut devenir le parent du 5e cluster, car il est vide (∅).

Construire une liste d'enfants pour chaque parent:

 0) 111111111            children: 1,4 1) .111111.. parent: 0, children: 2 2) ...1111.. parent: 1, children: 3 3) .....11.. parent: 2 4) .......11 parent: 0, children: 5 5) ......... parent: 4

Exclusion des enfants des parents:

 0) 1........            children: 1,4 1) .11...... parent: 0, children: 2 2) ...11.... parent: 1, children: 3 3) .....11.. parent: 2 4) .......11 parent: 0, children: 5 5) ......... parent: 4

À cette étape, nous devions obtenir une «topologie de réseau». Et nous l'avons. Si nous ne sommes intéressés que par l'emplacement des hôtes, alors cette «topologie de réseau» est tout à fait satisfaisante pour nous. Cependant, un autre commutateur est apparu dans notre réseau, dans lequel 0 hôte!

Pour tout réparer, il suffira après l'une des premières étapes d'éliminer ces «failles de données». Cela peut être fait immédiatement après la «binarisation»:

                                               ●  ●                                [] ►   [<strong>   (∅),    (⦱)</strong>]               [   ]                          [  ] ► /                [ "" ] ► /        [    ] [     ]              [   ] ►   ●                                        [???] ►   ●

Nous supprimons les ensembles vides (∅; « ......... »), mais pourquoi supprimer les univers (⦱; « 111111111 »)? La réponse deviendra apparente lorsque nous commencerons à mettre en œuvre la phase de «binarisation». Différentes variantes de la mise en œuvre de la «binarisation» peuvent produire à la fois « ......... » et « 111111111 » sur les mêmes données (données présentant le défaut décrit). Et, parce que il est aussi impossible d'obtenir " 111111111 " dans les données d'entrée correctes que d'obtenir " ......... ", alors nous pouvons supprimer tous les " 111111111 " (en plus, ils ne contiennent aucune information sauf que il y a des "défauts" dans les données).

Si vous appliquez cet algorithme (augmenté, corrigé) au même réseau (« Network_ serial »), la «topologie du réseau» ressemblera à ceci:

 0) 1........            children: 1,4 1) .11...... parent: 0, children: 2 2) ...11.... parent: 1, children: 3 3) .....11.. parent: 2 4) .......11 parent: 0

Note : , . , . , 2 ( “switch0”), 1 ( 2 ):

“ ”

 0) 11........            children: 1,4 1) ..11...... parent: 0, children: 2 2) ....11.... parent: 1, children: 3 3) ......11.. parent: 2 4) ........11 parent: 0

 0) 1......            children: 1,4 1) .1..... parent: 0, children: 2 2) ..1.... parent: 1, children: 3 3) ...11.. parent: 2 4) .....11 parent: 0

“ ”. “ ” “ ”. RingSync , ( : Pre‑order ). “ ” :

 1 1........ hostS/seed -> host0 -> . .11...... host1 -> host2 -> . ...11.... host3 -> host4 -> . .....11.. host5 -> host6 -> . .......11 host7 -> host8/leech

Note : (, ) , broadcast .

, “ ” ( ), (“ Network_ serial ”). ( ), . :

Schéma: connexion série des commutateurs; chemin de circulation pour une chaîne construite sans priorités

, “ ” (“ ”):

 ..........11 1 hS/seed -> h10 -> h11 -> ........11.. . h8 -> h9 -> ..111....... . h2 -> h3 -> h4 -> .....111.... . h5 -> h6 -> h7 -> 11.......... . h0 -> h1/leech

( “ ”) . , – 2, .. (∅). , “ ” , “ ” ( , ), (∅) ? , : ‑, “” , ( , ；）; ‑, ( ).

, “ ” , “ ”

: LLTR (clear), , “depth first traversal”

( ) , , “ ”, ‑ …

, “ ”, …

Note : , , . .

, ( ), .

 ..........11 1 hS/seed -> <strong>h11</strong> -> <strong>h10</strong> -> ........11.. . <strong>h9</strong> -> <strong>h8</strong> -> ..111....... . h2 -> h3 -> h4 -> .....111.... . h5 -> h6 -> h7 -> 11.......... . h0 -> h1/leech

“ Network_ serial ”…

, :

           switch0 -> switch1 -> switch2 -> switch3 -┐ switch4 <- switch0 <- switch1 <- switch2 <-----------┘

… “” “ switch0 <- switch1 <- switch2 ”. :

                                 switch0 -> switch4 -┐ switch3 <- switch2 <- switch1 <- switch0 <-----------┘

Schéma: connexion série des commutateurs; chemin de flux de trafic pour une chaîne prioritaire

, , , !

Note : , .. “ ”.

Note : “ ”, “ ” ( ; – L0 ) – .

, “ ” .

Note : , – .

() : “ ” ( LLTR 0:: : “ ” ) :

– ;
– ;
– ( );
– ( ) – , .

Note : “ – ” “ , ”, , , .

Note : – ( ). – ( ) . , ( ): ( ); ( ).

                                                    ●  ●                                     [] ►      [   (∅),    (⦱)]                    [   ]                               [  ] ► /                     [ "" ] ► /             [    ]    [     ]                   [   ] ►   ● [      /] ►   ●

“ ” “ Network_ serial ” :

 1 1........ hostS/seed -> host0 -> . .......11 host7 -> host8 -> . .11...... host1 -> host2 -> . ...11.... host3 -> host4 -> . .....11.. host5 -> host6/leech

“ ”, .

“ ” . “ ” :

 s0) ..........11 1 hS/seed -> h10 -> h11 -> s1) ........11.. . h8 -> h9 -> s3) ..111....... . h2 -> h3 -> h4 -> s4) .....111.... . h5 -> h6 -> h7 -> s5) 11.......... . h0 -> h1/leech

? , , , ( ):

 s0 -> s1 -> s2 -> s3 -┐  ┌- s4 <- s2 <------┘  └------> s2 -> s5

Note : “ s# ” “ ” (. ).

# TL;DR

(~~ k‑medoids ~~) + (∅), (⦱) + :
1. a _min a _max
2. 2
  1. + (∅), (⦱)
3. :
  1. ( : )
  2. ( O(nlogn) O(1) )
  3. ( nth_element implementations complexities )
4. a _medL (medLow) a _medR (medHi)
5. 2 ,
6. +
+ “” :
1. + “”
2. + bitCount ( max min)
:
1. min (min) (max) ( ) , ;
  bitCount(a _i )==bitCount(a _i |a _min ) , : a _i ==a _i |a _min
2. , ( ) –
3. min ( )
() :
1. ( “” “”)
:
1. “”, max , or|=a _i , a _max &=~or
  ( “ a _max ^=or ” – )
2. ( a _max a _min , .. , )
/:
1. (RingSync)

Note : , .

Hypothèse. ( ), .

“ , ”

, , (“ {…} ”) () . ():

 //    "  " int ...;{   //    "" }

“”, ():

 //==[Name]==// int ...;{   ... }

, :

? TensorsFlowing

c'est-à-dire – , “, ” – .

?
:

– ( ) , . “” , .. “” “” . , “ ”, .
– “” / , , . . , (Interprocedural optimization, Whole program optimization; Link‑time optimization) “” – .

Note : : .. (2D/3D , , *, …). (), , , ( , , 24 , ; , ACPI ), ( ) , ：（. (, , …) , ‑ . , , ‑. ( “” “”), “ *”. , – , , , . () – , . – ( ), . – , //‑/ /. (debug) ‑ .

Note : Debug , (, – { 9 , ; – ×16 ( 1.2 1.5); → }), warning' .

Note : , , , ‑. , , ( “ ” ) .

# Tooo Long; Didn't Read; Visualize, plz.

Note : , ( GIF “TensorsFlowing” “ ”). GIF “TensorsFlowing” GIF “ Loop over python list animation ”. , GIF , “ ” / . , ‑ 1:1, “ ”.

#

Note : GIF ( “Loop over python list animation”), . , , . ( ；）

Note : ( ) ( ). , .

Note : GIF ( “Scroll Down”) – (Ctrl+R), GIF . ( , ; , ‑ <oembed> ? )

 int average;{      int max,min;      max=min=countFill[i][0];      for(int j=1;j<numHosts;j++){            max=countFill[i][j]>max?countFill[i][j]:max;            min=countFill[i][j]<min?countFill[i][j]:min;      }      average=(max+min)/2; }

Note : GIF …

 int lo=0; struct CnN{      int Count; }iFill[numHosts]; for(int j=0,hi=numHosts-1;j<numHosts;j++){      if(countFill[i][j]<average) iFill[lo++].Count=countFill[i][j];      else                       iFill[hi--].Count=countFill[i][j]; } bitCluster[i]=0; if(lo==0||lo==numHosts) continue; //-

Note : ( ) .

 int averageMed;{      CnN *iFillLo=&iFill[0];      CnN *iFillHi=&iFill[lo];      const int hi=numHosts-lo;      if(lo>1) std::nth_element(iFillLo,&iFillLo[lo/2],&iFillLo[lo],[](const CnN a,const CnN b){return a.Count<b.Count;});      if(hi>1) std::nth_element(iFillHi,&iFillHi[hi/2],&iFillHi[hi],[](const CnN a,const CnN b){return a.Count<b.Count;});      averageMed=(iFillLo[lo/2].Count+iFillHi[hi/2].Count)/2; }

Note : std::nth_element() , , ( + = ).

 for(unsigned int j=0;j<numHosts;j++) bitCluster[i]|=( (countFill[i][j]<averageMed)?1:0 )<<j;

 bitCluster[i] = bitCluster[i]^(1<<((i/(numHosts-1))+(i%(numHosts-1)+1))%numHosts) ? bitCluster[i]:0;

Note : GIF . ReadMe ( ; ‑ , ).

‑ OMNeT++ “ ”, “ DAT_EX.h ”.

...

#

3‑ 1.92 , , 1.6 - 2 . , 3‑ ( ) ( Go – 2 , – 2 - 4 ). (4 ), 2.5 LLTR.

+ TODO' + .

, ‑ , , , 2 .

Note : , / , …

Spoiler

2 ?

, , . , , 2 . .

# Tooo Long; Didn't Read; Visualize, plz.

TODO[old]: (1 – gif_1, , 2 – gif_2, , …)

TODO: ,

? ( )

TODO: ( GIF “TensorsFlowing”, ‑ – ),

( Note, GIF , , , YouTube. : 4:2:0 TV‑ ( 16 - 235 ). , – (). : SVG – , “ ‑”; SWF – RIP)

# ?

( ), std (, ) ( );

( “ 1 ” == “ 1 ” ). Un exemple:

 0) 111111111111 1) 1111111111.. 2) 11111111.... 3) ..111....... 4) .....111.... <-  ,     2‑,  3‑ 5) 11..........

(.. ), .. “ 1 ” ( ) (. “ ” “ ”). “ 1 ”, ..:

 0) 111111111111 1) 1111111111.. 0 2) 11111111.... 1 3) ..111....... 2 4) .....111.... 2 5) 11.......... 4

( , – + (+), )

( “”). CPU, + . , , , , .

...

3: OMNeT++

LLTR 3: OMNeT++

Golang. ( , )

( , OMNeT++ c Qtenv)

( “background/fresh” “.ned” {“ grey99 ” → “ -,-,0;bgi=background/fresh ”}, “blueprint/print-26.png” Qtenv “LLTR 1:: ”)

( , “OMNetProject (v0.9) lltdapp”)

( , “hostS” – ( ) . , , – broadcast , unicast , .. – , . , – “ ”. “ – ”, : “ ” – “Serial” “ 1” ( – “ ”). – (, , broadcast unicast )[ rand , , – , – ])

( Precision Time Protocol (PTP) 2016-04-12)

( – , , “a3_v0.3_ft0.1.0”, “a3_v0.3.0” – , ; “ft” – fixed time)

TODO [x]: , , . “ TODO [x]” “ ” ( )

Références:

LLTR 4:

Wolfram Mathematica – Numbers (last episode 1 season) – .

∀ habrauser ∈ {user ∈ Habrahabr | user “”},

, “” .

(, . )

Références:

Get sequence (math induction) , online (Google Spreadsheets):
- Sequence
- Convert sequence dstId and srcId to i

, (hostsCount) – . . ? (: )

(, “”, {“”,“”,“”})

( ( ) [ ; “ ”], – n‑ “ ”; , LLTR, )

Permutation of bitsets (“lexicographic” order) derivation (mathematical induction)

( , __ [ , , , ]):

 n=4; k=2 bitset  i 0011 <- 0 0101 <- 1 1001 <- 2 0110 <- 3 1010 <- 4 1100 <- 5

Note: , .. bitset ^k _i < bitset ^k _i+1 , i – “ ”; k – ; n – .

“” ( ; /; , “”/), ?

( “B9”) ( “ ” O_o; , )
“ _tmain() ” ( )
, , – “ med() ” “ demed() ”

, :

:
“ ” (“ ”; “Permutations of multisets”).
Quelle est la différence? ( [abcdef]), ( [000011]).
, ( ):

 a => 0 b => 0 c => 0 d => 0 e => 1 f => 1

, , .. , , [abcdfe] ⇒ [000011], [000011] . (, )

{{000011}}.
{abcdef} 6! ( nuclphys.sinp.msu.ru/mathan/p1/m0204.html ).
.
, , ( [000011]) , ( (“1”) 2! × (“0”) 4! ) = 2! × 4! = 2! × (6−2)! .
= 6! ∕ (2! × (6−2)!).

( nuclphys.sinp.msu.ru/mathan/p1/m0204.html ), ( ru.wikipedia.org/wiki/?stable=1 ) – . . “ ” ( ru.wikipedia.org/wiki/?stable=1 ), “” “1” “0” – ( ru.wikipedia.org/wiki/?stable=1#___ ).

EN: → → combination: ( k‑combination with repetitions / k‑multicombination / multisubset ), ( en.wikipedia.org/wiki/Combination?stable=1#Example_of_counting_multisubsets ), “Stars and Bars” ( en.wikipedia.org/wiki/Stars_and_bars_(combinatorics)?stable=1#Proofs_via_the_method_of_stars_and_bars ). (/ ): “1” – Star, “0” – Bar.

, “Stars and Bars” “” ( “ ” – k‑combination with repetitions) “ ” (permutations of multisets): en.wikipedia.org/wiki/Permutation?stable=1#Permutations_of_multisets .
RU: ru.wikipedia.org/wiki/?stable=1#__

PS stackoverflow.com/a/24257996 , ( – : n!∕((n−k)!); n⩵k; (n−k)!⇒1; n! ).

PPS [ alisey Trif ] ‑ / ( “Permutations of multisets”), ?

5: OMNeT++ 2

LLTR 5: OMNeT++ 2

( LLTR-Process sequence, – { “LLTD-Process (vFinal)”}, – , i → dstId, )

Références:

6+7: +

LLTR 6:

, Golang.

Références:

Timers (QPC)

LLTR 7: (: “ ” – )

( 4 { //Wi‑Fi}, 3 ? – 2 ! – MacBook, Wi‑Fi Ethernet Thunderbolt)

( , “ ”, , “ ”)

( Wi‑Fi UDP broadcast – WNIC //. : How to override wifi broadcast speed limit? , Why does my UDP Broadcast wireless communication is capped at 1MBs? . 3 Mbps, 5 Mbps { }. MacBook {Wi‑Fi } Super‑, broadcast‑, unicast, {Wi‑Fi- ‑} unicast‑ broadcast { – Wi‑Fi}. , Wi‑Fi- – CPU . ‑.)

( UDP‑, !? : Windows “” {Windows NIC ?..}, API, “ CPU” { Win8 API, … (. “LLTD/flood/main.go”)}. “ ”. – API , “” . *nix { API}, , “” {. “LLTD/flood/main.go”}. : “ iperf3 and microbursts ”)

( → . { ; SMB}: → → → MacBook . , .)

( “LLTD/Prepare test environment.txt”)

Références:

GoLLTD

( “LLTD/Client.go”, “‑” – “LLTD/flood/main.go”)

( {Client1} NIC , – , , “ ” : “ interface always dead”)

Note: – Wi‑Fi ( ADSL‑/, ADSL – )

Note: ‑ : “” 100 Mbps unicast ; 100 Mbps broadcast . ( , /, )

TODO : : ( – ; ; +1/−1 ). Google Wave, Google Docs, Discus. Format:

–
– ,
:
- , (.. ) – “” “ ” – (.. “” )

UserJS/UserCSS, , , .. , .

– – , UI (, , ) ( , “”). “” UserCSS. , , , ( ), ( ) ( ).

( ) ( ). ( UserJS UserCSS; Opera Presto , Firefox )

– “ OMNeT++ 2”.

TODO [x]: () + , + , , OMNeT++ v5.0b1 INET v3.0.0 + , ( ), – /

OMNetProjectLLTD lltdapp + sim – LLTR , “LLTD” (“R” – “D”, //) [ “ 1”, .. article_1 a1_v0.30.0 ] { , }
OMNetProject (before v0.9) lltdapp – (“LLTDClient.cc”: , DISCARD‑ “” ARP) [ article_1 ] { “for diff (LLTR)” – (diff) , , }
OMNetProject (v0.9) lltdapp – (“LLTDClient.cc”: “ trafCount[stepN]++ ”): (. “ timeCalcEnd ” “ timeoutCalc ”), (“stat.txt”: ) [ 3] { “ , ”, .. , }
Timers (QPC) – – ( “Timers.cpp”; “ The Windows Timestamp Project: Adjustment of System Time (NTP) ”) [ 6] { , Golang, “ 6”}
OMNetProject (v0.9.1) lltdapp – , : (“LLTDClient.cc”: “ sntpTimeOffset ” “ sntpLatency ” – , ) [ 3]
“fixed event time” – :
- OMNetProject (fixed event time — v0.9.2) lltdapp – , “stat.txt” [ 3]
OMNetProject (v0.9.3) lltdapp – v0.9.1 + , + v0.9.2ft [ 3]
Get sequence (math induction) – : unicast_src_host _i+1 = unicast_dst_host _i , .. , (unicast dst), , (unicast src) [ 4] { , “” ( ) – “” , : “ ” ( ), , , }
OMNetProject (v0.9.4) lltdapp – : , “ ” [ 5]
OMNetProject (vFinal) lltdapp – [ 5]
LLTD-Process (vFinal) – [ 5]
GoLLTD – Go (“LLTD/old/main.old.go”) + + (“LLTD/Prepare test environment.txt”) + , : “Timers/”, “SNTP/”, “LLTD/flood/broadcast.txt”, “LLTD/Prepare test environment.txt”, “LLTD/flood/old/main.go”, “LLTD/flood/main.go”, “LLTD/” [ 6,7]

( ) (), . “ ” – , .

Note : – , ( ) – .

“ ”, , “ ”.

“ ”, , :

– . , – “ ”.

Note : “” – ( ⁻¹ ) ( ) (: ; ; – ); “‑‑‑” – ( ) , , ( ), , { “” ( ) – , , “ ?”; + “ ' ', ”, : (cookie) view‑only}

Note : (‑)

LLTD v1 – TCP ( map?), ,
() ,

LLTD v0.9 – client , ( )

v0.5 Go
IP, github.com/hashicorp/mdns
github.com/davecheney/mdns
grokbase.com/t/gg/golang-nuts/132tcpawde/go-nuts-udp-multicast-who-is-on-my-network

PS ( ) “ ”.
r=rand();
r, .
:
1. ‑ . , – . + ± ( “” ).
2. “”. ( , ; ) + ( “” )

iperf3 and microbursts burntchrome.blogspot.ru/2016/09/iperf3-and-microbursts.html

# Check‑list (TODO's)

TODO, .

PNG{SVG} (SVG thumbnail PNG) :

PNG:

[ 778px, 756px] ‑ ( . )
‑ 7z (un[7z]me), ( – “ ”, ‑ , ‑ )
- [ Photoshop] “Save for Web” → PNG 24+alpha
- [ GIMP] “8bpc RGBA” ( ), “ Save for Web ”
256 + alpha‑
- [ Adobe Fireworks] (Ctrl+Shift+X) → PNG‑8 + alpha
- []
  - ImageAlpha ( pngquant + pngnq-s9 + posterizer )
  - Color Quantizer

“” , Image Catalyst ( “” 2 : 2.1 2.5 , ):

“” Image Catalyst 2.1 ([5] Xtreme profile)

Tools\config.ini

 [options] ;         ,    "true"  "false". fs = true ;    PNG.    0,       %NUMBER_OF_PROCESSORS%. threatpng = 0 ; .          ,    "true"  "false". up = false [JPEG] ; Metadata.       Metadata  JPEG,    "true"  "false" ,   . dc = true   ;Delete comment field (as left by progs like Photoshop & Compupic). de = true   ;Strip Exif section (smaller JPEG file, but lose digicam info). di = true   ;Delete IPTC section (from Photoshop, or Picasa). dx = true   ;Deletex XMP section. du = true   ;Delete non image sections except for Exif and comment sections. [PNG] ; ColorType  BitDepth.      ColorType  BitDepth  PNG,    "true"  "false". nc = true ; -.       "Dirty Transparency"  PNG c -,    "true"  "false". na = true ; Chunks. ;     Chunks   Chunks,   "remove"       Chunks   Chunks,   . ;     Chunks   Chunks,   "keep"       Chunks   Chunks,   . ; Chunks: ;text = iTXt,tEXt,zTXt ;color = cHRM,sRGB,iCCP,gAMA ;misc = bKGD,pHYs,sBIT,sPLT,hIST,tIME ;all  = all of noncritical chunks hunks = remove all

Note : “ Image Catalyst 2.1 . Enter. ”, , , ( “Image Catalyst 2.1” “Image-Catalyst-2.1”)

“” Image Catalyst 2.5 ([1] Xtreme profile)

Tools\config.ini

 [options] ;Number of streams. If value early 0, is used value of parameter %NUMBER_OF_PROCESSORS%. thread=0 ;Automatic replacement of original images by the optimized. outdir=true ;Check update update=false [PNG] ;Parameters of optimization of PNG: ;/a# - PNG dirty transparency 0=Clean, 1=Optimize; ;/g# - PNG gamma 0=Remove, 1=Apply & Remove, 2=Keep; ;/na - PNG don't change RGB values for fully transparent pixels; ;/nc - PNG don't change ColorType and BitDepth; ;/np - PNG don't change Palette. xtreme=/a1 /g0 advanced=/a0 /g0 ;Remove PNG Metadata (Chunks). chunks=true [JPEG] ;Remove JPEG Metadata. metadata=true [GIF] ;Remove GIF Metadata. giftags=true

Note : “ Attention: running 2 of Image Catalyst. ”, , , ( “iCatalyst-2.5”)

merge_min.bat

 @echo off setlocal enabledelayedexpansion :: Copy file from source to destination directory only if :: source file is smaller in size than in destination directory echo Src dir: %~f1 echo Dst dir: %~f2 echo --- for /r "%~1" %%A in (*) do ( set FileA=%%~fA set FileB=!FileA:%~f1=%~f2! set FileASize=%%~zA for %%Z in ("!FileB!") do set FileBSize=%%~zZ if !FileASize! LSS !FileBSize! copy "!FileA!" "!FileB!" )

“.svg” ( ) – (SVG) (un[7z]me)

SVG:
1. {SVG 1.1; UTF-8; ; : ; : “1:100”; } ( , 2 – 1‑ )
2. transform SVG ( 90 ) ( SVG ):
  1. DevTools transform ( “ [transform] ”)
  2. “ Rotate90AndSwapWH() ” ( “ ”)
    Rotate90AndSwapWH()
    Sub Rotate90AndSwapWH() Dim sr As ShapeRange, s As Shape, w#, h# Set sr = ActiveSelectionRange On Error Resume Next boostStart2 "Rotate 90 and Swap WH" For Each s In sr s.GetSize w, h s.Rotate -90 s.SetSizeEx s.CenterX, s.CenterY, w, h Next s boostFinish2 End Sub
    
    + boostStart2/boostFinish2:
    
    github.com/cdrpro-macros/cdr-tools/blob/master/source/sToolsBoost.bas
    CorelDRAW
    
    :
    
    Private Sub boostStart2(ByVal unDo$) On Error Resume Next ActiveDocument.BeginCommandGroup unDo Optimization = True EventsEnabled = False End Sub Private Sub boostFinish2() On Error Resume Next EventsEnabled = True Optimization = False ActiveWindow.Refresh ActiveDocument.EndCommandGroup 'Refresh End Sub
3. :
  - :
    - ( [, ] )
    - ( )
4. ( )
5. XML ( )
  1. ( ):
    - “ DOCTYPE ” “ Creator ” “ 96ppi ” ( ppi CorelDRAW SVG)
    - “ metadata ”, “ id ” ( )
    - svg:
      1. “ xmlns ” “ xml:space ”
      2. “ xmlns:xlink ”
      3. [, “ style ” “ fill-rule:evenodd; clip-rule:evenodd ”] “ version ” “ style ” ` style="margin:16px auto" shape-rendering="geometricPrecision" fill-rule="evenodd" clip-rule="evenodd" xmlns="http://www.w3.org/2000/svg" version="1.1" baseProfile="full" `
    - ( ) ` " ` ` " `
  2. ( <rect> <g>), , “ viewBox ” ( <svg>)
    - , SVG , CorelDRAW – , , , ( , )
  3. SVG optimiser :
    - :
      - Whitespace: pretty
      - Style type: optimal
      - Truncate * numbers: unchanged
      - ( , “Remove clean group”, )
    - <svg>
    - <style> – SVG optimiser CDATA ( )
  4. XML

PNG SVG:

“PNG_SVG.bat” ( 7-Zip SVG: “ -txz -m0=LZMA2:lc1:pb0 -mx ”)

PNG_SVG.bat

 @echo off setlocal enabledelayedexpansion :: PNG+7Zip{SVG} echo PNG dir: %~f1 echo SVG dir: %~f2 echo --- for /r "%~2" %%A in (*.svg) do ( set SVG=%%~fA set PNG=!SVG:%~f2=%~f1!.png "%ProgramFiles%\7-Zip\7z.exe" a dummy -txz -m0=LZMA2:d96m:fb74:lc1:pb0 -mx -so -- "!SVG!" >> "!PNG!" )

“ LZMA2:d96m:fb74:lc1:pb0 ”?

‑ ( “RingSync_no_problem.svg”):

 - "LZMA2:d96m:fb64"        6804 byte - "LZMA2:d96m:fb74"        6800 byte - "LZMA2:d96m:fb74:lc2"    6812 byte - "LZMA2:d96m:fb57:lc2"    6780 byte - "LZMA2:d96m:fb57:lc1"    6768 byte - "LZMA2:d96m:fb56:lc1"    6760 byte - "LZMA2:d96m:fb49:lc1"    6760 byte - "LZMA2:d96m:fb56:lc1:pb0" 6696 byte - "LZMA2:d96m:fb46:lc1:pb0" 6688 byte (fb44-fb47) - "LZMA2:d96m:fb63:lc1:pb0" 6688 byte - "LZMA2:d96m:fb66:lc1:pb0" 6684 byte - "LZMA2:d96m:fb74:lc1:pb0" 6692 byte

svg “ LZMA2:d96m ” (fb64), “ LZMA2:d96m:fb74:lc1:pb0 ” .

Note : Image Catalyst: ping timeout, ( 2.5) ( 2.1 – )

Image Catalyst.bat

v2.1 diff:

 182c182 < if defined thrt >nul 2>&1 ping -n 1 -w 500 127.255.255.255 & goto:waithreat --- > if defined thrt >nul 2>&1 timeout /t 1 /nobreak & goto:waithreat 203c203 < 1>nul 2>&1 ping -n 1 -w 500 127.255.255.255 --- > 1>nul 2>&1 timeout /t 1 /nobreak 237c237 < if exist "%~1" (1>nul 2>&1 ping -n 1 -w 500 127.255.255.255 & goto:waitflag) --- > if exist "%~1" (1>nul 2>&1 timeout /t 1 /nobreak & goto:waitflag) 513c513 <     if exist "%tmppath%\typelog.lck" (1>nul 2>&1 ping -n 1 -w 500 127.255.255.255 & goto:savelog) --- >     if exist "%tmppath%\typelog.lck" (1>nul 2>&1 timeout /t 1 /nobreak & goto:savelog) 534c534 < if "%jpeg%" equ "0" if "%png%" equ "0" 1>nul ping -n 1 -w 500 127.255.255.255 2>nul & goto:finmessage --- > if "%jpeg%" equ "0" if "%png%" equ "0" 1>nul timeout /t 1 /nobreak 2>nul & goto:finmessage 572c572 <     1>nul ping -n 1 -w 500 127.255.255.255 2>nul --- >     1>nul timeout /t 1 /nobreak 2>nul

V2.5 diff:

 319,320c319 <     call:division float 1024 100 <     call:echostd " In   - !float! " --- >     call:echostd " In   - !float! " 322d320 <     call:division change 1024 100 324,325c322 <     call:division float 1024 100 <     call:echostd " Out  - !float!  (!change! , %5%%%%%%)" --- >     call:echostd " Out  - !float!  (!change! , %5%%%%%%)" 362,363c359,360 < set /a "ww=%random%%%%1" < 1>nul 2>&1 ping -n 1 -w %ww% 127.255.255.255 --- > set /a "ww=%random%%%%1/1000" > 1>nul 2>&1 timeout /t %ww% /nobreak 707c704 < if %jpeg% equ 0 if %png% equ 0 if %gif% equ 0 1>nul 2>&1 ping -n 1 -w 500 127.255.255.255 & goto:finmessage --- > if %jpeg% equ 0 if %png% equ 0 if %gif% equ 0 1>nul 2>&1 timeout /t 1 /nobreak & goto:finmessage 741d737 < call:division changePNG 1024 100 747d742 < call:division changeJPG 1024 100 753d747 < call:division changeGIF 1024 100 800c794 <     call:echostd " Total %1:        %%change%1%% , %%perc%1%%%%%%" --- >     call:echostd " Total %1:        %%change%1%% , %%perc%1%%%%%%"

Note : Image Catalyst ( ) CP866, diff, , .

778px – (780px – − 2px )
- 756px – (758px – − 2px )
- 738px – (740px – − 2px )
Image Catalyst v2.1 v2.5, ( “ merge_min.bat ”).
– : habrastorage “dwbmwbyvlzes80cep1hvcdb5iy.png” () HTTP‑ “ Content-Disposition : inline ;... ”, , , (): “dwbmwbyvlzes80cep1hvcdb5iy.png#real-name.png”. , – ( ). SVG – (), , …
(id, name). . ( – , , – )
, ( ).
‑ (un[7z]me), habrastorage – , CloudFlare Polish .

Note : habrastorage SVG ( ): ( ), PNG{SVG} ( SVG, , – ) ( , , / – ‑ / , )

git:

git tag git “git-tag-‹›” .
git , / , “article_#”. ( LLTR Simulation Model )

( “http”), ( ) web.archive.org, sohabr.net:

 var res=str.match(/http[^#)\s]*/gm); var res_l=res.length; for(var i=0;i<res_l;i++) console.log(res[i]); var archive = res.filter(function(a){return a.search(/(omnetpp.org\/doc\/omnetpp\/manual\/#|wikipedia|\/github.com\/)/)==-1;});

, web.archive.org sohabr.net .
habrahabr.ru habr.com, .. web.archive.org ( , ).

, Wikipedia “?stable=1”.
() MediaWiki (“#.D0.AD.D0.B2.D1.80.D0.B8.D1.81…”; “wikipedia”, “#.D0”) (“#…”).
C ( ) + Git.
[ “ 2”] (“LLTR #::”), “title” ( ).
(id, name), (, “#”) ( title “ ”).
- sohabr.net ` id ` ( ), ` <a name=""></a> `?
- “Unicode Link Symbol” (U+1F517; “🔗”) , (Chrome , , ), .. .
(<hr />) – , UserCSS ( UserCSS ).
` <p><br /></p> `, UserCSS ` <br /> `, ` margin ` ` <p> ` ( ).
- ~~`<p> ` , Markdown…~~ (, ` <p> ` info , , UserCSS, ).
height ( ‑), , width.
“ Full width brackets ” ( ; , ).
“ ?”
- ( , , ). , ( ) , . , – . , ( ). /, . //, – .
- “ ”.
habrahabr.ru/info/help/posts/ ( , old )
, how‑to – « » (tutorial), ;
.

Note : habrahabr <oembed> , GitHub , .

Note : TODO‑ , 43 KiB ( “ 0”), 69 KiB ( “ 1”), 45 KiB ( ).

LLTR Partie 2: Algorithme pour déterminer la topologie du réseau à partir des statistiques collectées

# TL;DR

# Tooo Long; Didn't Read; Visualize, plz.

#

...

#

# Tooo Long; Didn't Read; Visualize, plz.

# ?

LLTR 3: OMNeT++

LLTR 4:

LLTR 5: OMNeT++ 2

LLTR 6:

LLTR 7: (: “ ” – )

# Check‑list (TODO's)

More articles: