J'ai lutté contre la tentation de nommer l'article quelque chose comme "L'inefficacité terrifiante des algorithmes STL" - vous savez, juste pour le plaisir de me former à l'art de créer des titres flashy. Mais néanmoins, il a décidé de rester dans les limites de la décence - il vaut mieux obtenir des commentaires des lecteurs sur le contenu de l'article que l'indignation face à son grand nom.
À ce stade, je suppose que vous connaissez un peu le C ++ et le STL, et que vous prenez également soin des algorithmes utilisés dans votre code, de leur complexité et de leur pertinence pour les tâches.
Des algorithmes
L'un des conseils bien connus que vous pouvez entendre de la communauté des développeurs C ++ modernes n'est pas de proposer des vélos, mais d'utiliser des algorithmes de la bibliothèque standard. C'est un bon conseil. Ces algorithmes sont sûrs, rapides et testés au fil des ans. Je donne également souvent des conseils sur leur application.
Chaque fois que vous voulez en écrire un autre - vous devez d'abord vous souvenir s'il y a quelque chose dans la STL (ou boost) qui résout déjà ce problème sur une ligne. S'il y en a, il est souvent préférable de l'utiliser. Cependant, dans ce cas, nous devons également comprendre quel type d'algorithme se cache derrière l'appel de la fonction standard, quelles sont ses caractéristiques et ses limites.
Habituellement, si notre problème correspond exactement à la description de l'algorithme de STL, ce serait une bonne idée de le prendre et de l'appliquer "front". Le seul problème est que les données ne sont pas toujours stockées sous la forme sous laquelle l'algorithme implémenté dans la bibliothèque standard souhaite les recevoir. Ensuite, nous pouvons avoir l'idée de convertir d'abord les données, puis d'appliquer toujours le même algorithme. Eh bien, vous savez, comme dans cette blague mathématique «Éteignez le feu de la bouilloire. La tâche est réduite à la précédente. »
Intersection d'ensembles
Imaginez que nous essayons d'écrire un outil pour les programmeurs C ++ qui trouvera tous les lambdas dans le code avec la capture de toutes les variables par défaut ([=] et [&]) et affichera des astuces pour les convertir en lambdas avec une liste spécifique de variables capturées. Quelque chose comme ça:
std::partition(begin(elements), end(elements), [=] (auto element) {
Dans le processus d'analyse du fichier avec le code, nous devrons stocker la collection de variables quelque part dans la portée actuelle et environnante, et si un lambda est détecté avec la capture de toutes les variables, comparer ces deux collections et donner des conseils sur sa conversion.
Un ensemble avec des variables dans la portée parent et un autre avec des variables à l'intérieur du lambda. Pour former un conseil, le développeur n'a qu'à trouver leur intersection. Et c'est le cas lorsque la description de l'algorithme de STL est juste parfaite pour la tâche:
std :: set_intersection prend deux ensembles et retourne leur intersection. L'algorithme est beau dans sa simplicité. Il prend deux collections triées et les parcourt en parallèle:
- Si l'élément actuel dans la première collection est identique à l'élément actuel dans la seconde - ajoutez-le au résultat et passez aux éléments suivants dans les deux collections
- Si l'élément actuel dans la première collection est inférieur à l'élément actuel dans la deuxième collection, passez à l'élément suivant dans la première collection
- Si l'élément actuel de la première collection est plus grand que l'élément actuel de la deuxième collection, passez à l'élément suivant de la deuxième collection
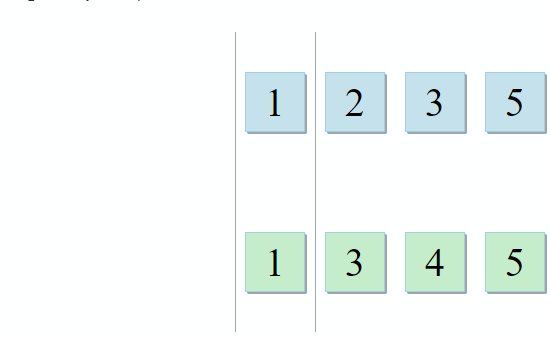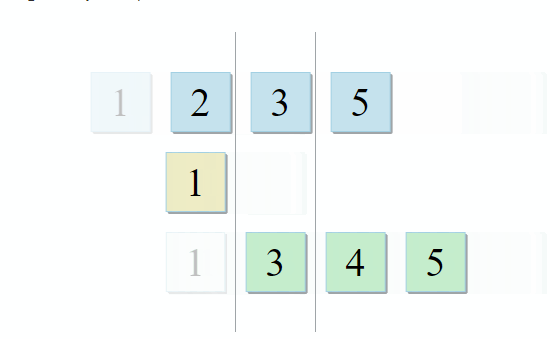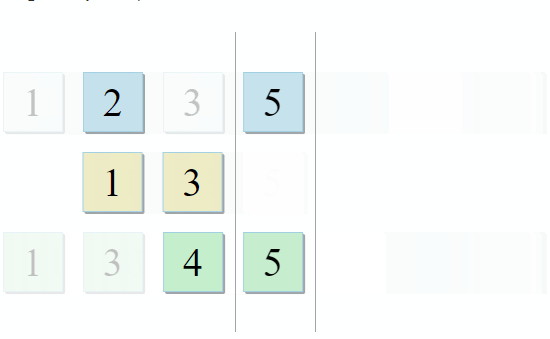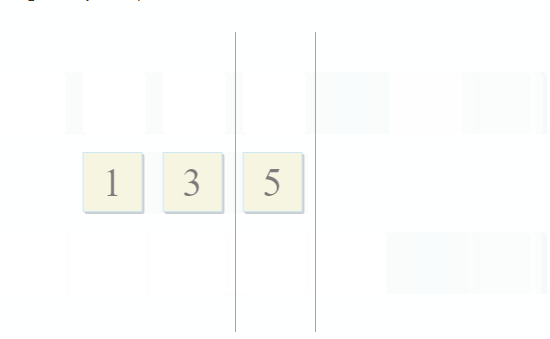
À chaque étape de l'algorithme, nous nous déplaçons le long de la première, de la seconde ou des deux collections, ce qui signifie que la complexité de cet algorithme sera linéaire - O (m + n), où n et m sont les tailles des collections.
Simple et efficace. Mais ce n'est que jusqu'à présent que les collections en entrée sont triées.
Tri
Le problème est que, en général, les collections ne sont pas triées. Dans notre cas particulier, il est pratique de stocker des variables dans une structure de données semblable à une pile en ajoutant des variables au niveau de pile suivant lors de la saisie d'une étendue imbriquée et en les supprimant de la pile lorsque vous quittez cette étendue.
Cela signifie que les variables ne seront pas triées par nom et que nous ne pouvons pas utiliser directement std :: set_intersection sur leurs collections. Étant donné que std :: set_intersection nécessite des collections exactement triées à l'entrée, l'idée peut surgir (et j'ai souvent vu cette approche dans des projets réels) de trier les collections avant d'appeler la fonction de bibliothèque.
Dans ce cas, le tri supprimera l'idée d'utiliser une pile pour stocker des variables en fonction de leur portée, mais cela est toujours possible:
template <typename InputIt1, typename InputIt2, typename OutputIt> auto unordered_intersection_1(InputIt1 first1, InputIt1 last1, InputIt2 first2, InputIt2 last2, OutputIt dest) { std::sort(first1, last1); std::sort(first2, last2); return std::set_intersection(first1, last1, first2, last2, dest); }
Quelle est la complexité de l'algorithme résultant? Quelque chose comme O (n log n + m log m + n + m) est une complexité quasi-linéaire.
Moins de tri
Ne pouvons-nous pas utiliser le tri? Nous pouvons, pourquoi pas. Nous allons simplement rechercher chaque élément de la première collection dans la deuxième recherche linéaire. On obtient la complexité O (n * m). Et j'ai aussi vu cette approche dans de vrais projets assez souvent.
Au lieu des options «trier tout» et «ne rien trier», nous pouvons essayer de trouver Zen et emprunter la troisième voie - trier une seule des collections. Si l'une des collections est triée, mais pas la seconde, alors nous pouvons parcourir les éléments de la collection non triée une par une et les rechercher dans la recherche binaire triée.
La complexité de cet algorithme sera O (n log n) pour trier la première collection et O (m log n) pour rechercher et vérifier. Au total, on obtient la complexité O ((n + m) log n).
Si nous décidons de trier une autre des collections, nous obtenons la complexité O ((n + m) log m). Comme vous le comprenez, il serait logique de trier ici une collection plus petite pour obtenir la complexité finale O ((m + n) log (min (m, n))
L'implémentation ressemblera à ceci:
template <typename InputIt1, typename InputIt2, typename OutputIt> auto unordered_intersection_2(InputIt1 first1, InputIt1 last1, InputIt2 first2, InputIt2 last2, OutputIt dest) { const auto size1 = std::distance(first1, last1); const auto size2 = std::distance(first2, last2); if (size1 > size2) { unordered_intersection_2(first2, last2, first1, last1, dest); return; } std::sort(first1, last1); return std::copy_if(first2, last2, dest, [&] (auto&& value) { return std::binary_search(first1, last1, FWD(value)); }); }
Dans notre exemple avec les fonctions lambda et la capture de variables, la collection que nous allons trier sera généralement la collection de variables utilisées dans le code de la fonction lambda, car il y aura probablement moins de variables que les variables de la portée lambda environnante.
Hachage
Et la dernière option discutée dans cet article sera d'utiliser le hachage pour une plus petite collection au lieu de la trier. Cela nous donnera l'occasion de rechercher O (1), bien que la construction du hachage, bien sûr, prendra un certain temps (de O (n) à O (n * n), ce qui peut devenir un problème):
template <typename InputIt1, typename InputIt2, typename OutputIt> void unordered_intersection_3(InputIt1 first1, InputIt1 last1, InputIt2 first2, InputIt2 last2, OutputIt dest) { const auto size1 = std::distance(first1, last1); const auto size2 = std::distance(first2, last2); if (size1 > size2) { unordered_intersection_3(first2, last2, first1, last1, dest); return; } std::unordered_set<int> test_set(first1, last1); return std::copy_if(first2, last2, dest, [&] (auto&& value) { return test_set.count(FWD(value)); }); }
L'approche de hachage sera un gagnant absolu lorsque notre tâche consistera à comparer systématiquement un petit ensemble A avec un ensemble d'autres (grands) ensembles B₁, B₂, B .... Dans ce cas, nous devons construire un hachage pour A une seule fois, et nous pouvons utiliser sa recherche instantanée pour le comparer avec les éléments de tous les ensembles B considérés.
Test de performance
Il est toujours utile de confirmer la théorie par la pratique (en particulier dans des cas comme celui-ci, lorsqu'il n'est pas clair si les coûts initiaux du hachage seront rentables avec un gain de performances de recherche).
Dans mes tests, la première option (avec le tri des deux collections) a toujours donné les pires résultats. Le tri d'une seule collection plus petite fonctionnait un peu mieux sur des collections de même taille, mais pas trop. Mais les deuxième et troisième algorithmes ont montré une augmentation très significative de la productivité (environ 6 fois) dans les cas où l'une des collections était 1000 fois plus grande que l'autre.