Nous continuons notre cycle sur le dispositif de blockchain Monero, et l'article d'aujourd'hui sera consacré au protocole RingCT (Ring Confidential Transactions), qui présente les transactions confidentielles et les nouvelles signatures de sonnerie. Malheureusement, il existe peu d'informations sur Internet sur son fonctionnement, et nous avons essayé de combler cette lacune.

Nous parlerons de la façon dont le réseau cache le nombre de transferts utilisant ce protocole, pourquoi nous avons refusé les signatures en anneau classiques pour cryptonote et comment cette technologie se développera.
Étant donné que ce protocole est l'une des technologies les plus complexes de Monero, le lecteur aura besoin de connaissances de base sur le dispositif de cette blockchain et de connaissances superficielles en cryptographie sur courbes elliptiques (pour rafraîchir ces connaissances, vous pouvez lire les premiers chapitres de notre article précédent sur les
multi-signatures ).
Protocole RingCT
L'une des attaques possibles contre les devises cryptonote est l'analyse de la blockchain basée sur la connaissance du montant et de l'heure de la transaction envoyée. Il permet
restreindre considérablement la recherche des sorties qui intéressent l'attaquant. Pour se protéger contre une telle analyse, Monero a introduit un protocole de transaction anonyme qui masque complètement le montant des transferts sur le réseau.
Il convient de noter que l'idée de cacher des montants n'est pas nouvelle. L'un des premiers à le décrire a été le développeur de Bitcoin Core, Greg Maxwell, dans son
article sur les transactions confidentielles . L'implémentation actuelle de RingCT est sa modification avec la possibilité d'utiliser des signatures en anneau (sans elles), et a ainsi obtenu son nom - Ring Confidential Transactions.
Entre autres choses, le protocole aide à se débarrasser des problèmes de mélange des sorties de poussière - sorties pour une petite quantité (généralement obtenues sous la forme de modifications des transactions), ce qui a créé plus de problèmes qu'ils n'en ont coûté.
En janvier 2017, le réseau de hard fork Monero a été organisé, permettant l'utilisation facultative de transactions confidentielles. Et en septembre de la même année, avec la version 6 hard fork, ces transactions sont devenues les seules autorisées sur le réseau.
RingCT utilise plusieurs mécanismes à la fois: les signatures de groupe anonyme spontané à liaisons multiples (ci-après - MLSAG), les engagements Pedersen et les preuves de portée (ce terme n'a pas de traduction établie en russe).
Le protocole RingCT introduit deux types de transactions anonymes: simples et complètes. Le premier portefeuille génère lorsqu'une transaction utilise plus d'une entrée, la seconde - dans la situation opposée. Ils diffèrent par la validation des montants de transaction et les données signées par la signature MLSAG (nous en parlerons plus loin ci-dessous). De plus, les transactions de type complet peuvent être générées avec n'importe quel nombre d'entrées, il n'y a pas de différence fondamentale. Le livre
«Zero to Monero» sur ce sujet indique que la décision de limiter les transactions complètes à une entrée a été prise à la hâte et pourrait changer à l'avenir.
Signature MLSAG
Rappelez-vous ce que sont les entrées signées d'une transaction. Chaque transaction dépense de l'argent et génère. Les fonds sont générés en créant des sorties de transaction (une analogie directe avec les billets de banque), et la sortie qu'une transaction dépense (après tout, dans la vie réelle, nous dépensons des billets de banque) devient une entrée (soigneusement, il est très facile de se confondre ici).
L'entrée fait référence à plusieurs sorties, mais n'en dépense qu'une, créant ainsi un «écran de fumée» qui rend difficile l'analyse de l'historique des traductions. Si une transaction a plus d'une entrée, alors une telle structure peut être représentée sous la forme d'une matrice, où les lignes sont des entrées et les colonnes sont des sorties de pétrissage. Pour prouver au réseau que la transaction passe ses sorties (connaît leurs clés secrètes), les entrées sont signées avec une signature en anneau. Une telle signature donne la garantie que le signataire connaissait les clés secrètes de tous les éléments de l'une des colonnes.
Les transactions confidentielles n'utilisent plus les signatures en anneau
cryptonote classiques, elles ont été remplacées par MLSAG, une version à entrées multiples des signatures en anneau monocouche similaires,
LSAG .
Ils sont appelés multicouches car ils signent plusieurs entrées à la fois, chacune étant mélangée à plusieurs autres, c'est-à-dire qu'une matrice est signée, pas une ligne. Comme nous le verrons plus tard, cela permet d'économiser sur la taille de la signature.
Voyons comment se forme une signature en anneau, en utilisant l'exemple d'une transaction qui dépense 2 sorties réelles et utilise m - 1 au hasard de la blockchain pour pétrir. Indiquez les clés publiques des sorties que nous dépensons
, et des images clés pour eux respectivement:
Ainsi, nous obtenons une matrice de
2 x m . Tout d'abord, nous devons calculer les soi-disant défis pour chaque paire de sorties:
Nous commençons les calculs avec les sorties que nous dépensons en utilisant leurs clés publiques:
et des nombres aléatoires
En conséquence, nous obtenons les valeurs:
que nous utilisons pour calculer le défi
la paire de sorties suivante (pour faciliter la compréhension de la substitution, nous avons mis en évidence ces valeurs dans différentes couleurs). Toutes les valeurs suivantes sont calculées dans un cercle selon les formules données dans la première illustration. Le défi pour une paire de sorties réelles est calculé en dernier.
Comme nous pouvons le voir, dans toutes les colonnes, à l'exception de celle contenant les sorties réelles, des nombres générés aléatoirement sont utilisés
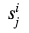
. Pour la πième colonne, nous en avons également besoin. Convertir
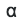
en s:
La signature elle-même est un tuple de toutes ces valeurs:
De plus, ces données sont inscrites dans la transaction.
Comme nous pouvons le voir, MLSAG ne contient qu'un seul défi
c 0 , ce qui permet d'économiser sur la taille de la signature (qui nécessite déjà beaucoup d'espace). Ensuite, tout réviseur utilisant les données
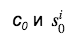
, restaure les valeurs c
1 , ..., c
m et vérifie que

. Ainsi, notre bague a été fermée et la signature a été vérifiée.
Pour les transactions RingCT de type full, une ligne supplémentaire est ajoutée à la matrice avec des sorties mixtes, mais nous en parlerons ci-dessous.
Engagements Pedersen
Des schémas d'engagement (utilisent souvent le terme anglais - engagements) sont utilisés pour qu'une partie puisse prouver qu'elle connaît un certain secret (nombre), sans le révéler réellement. Par exemple, vous jetez un certain nombre sur les os, envisagez l'engagement et le transmettez à la partie de confiance. Ainsi, au moment de révéler le numéro secret, l'inspecteur considère indépendamment l'engagement, s'assurant ainsi que vous ne l'avez pas trompé.
Les engagements Monero sont utilisés pour masquer le montant des transferts et utilisent l'option la plus courante - les engagements Pedersen. Soit dit en passant, un fait curieux - au début, les développeurs ont suggéré de cacher les montants avec le pétrissage habituel, c'est-à-dire d'ajouter des extrants à des montants arbitraires pour introduire de l'incertitude, mais sont ensuite passés à des engagements (ce n'est pas un fait qu'ils ont économisé sur la taille de la transaction, comme nous le verrons ci-dessous).
En général, l'engagement est le suivant:
Où
C est la valeur de l'engagement lui-même,
a est le montant à masquer,
H est le point fixe sur la courbe elliptique (générateur supplémentaire) et
x est un masque arbitraire qui cache le facteur généré aléatoirement. Le masque est nécessaire ici afin que le tiers ne puisse pas sélectionner la valeur de l'engagement avec une simple force brute.
Lors de la génération d'une nouvelle sortie, le portefeuille calcule un engagement pour celui-ci, et lors de sa dépense, il prend soit la valeur calculée lors de la génération, soit il la recompte, selon le type de transaction.
Ringct simple
Dans le cas de transactions RingCT simples, afin de garantir que la transaction crée des extrants égaux à la somme des intrants (ne rapporte pas d'argent), les engagements des premier et deuxième doivent être les mêmes, c'est-à-dire:
Les commissions d'engagement considèrent un peu différent - sans masque:
, où
a représente le montant de la commission, il est accessible au public.
Cette approche nous permet de prouver à la partie utilisatrice que nous utilisons les mêmes montants sans les révéler.
Pour clarifier les choses, regardons un exemple. Supposons qu'une transaction dépense deux sorties (c'est-à-dire qu'elles deviennent des entrées) sur 10 et 5 XMR et génère trois sorties totalisant 12 XMR: 3, 4 et 5 XMR. Dans le même temps paie une commission de 3 XMR. Ainsi, le montant d'argent dépensé plus le montant généré et la commission est égal à 15 XMR. Essayons de calculer les engagements et examinons la différence dans leurs montants (rappelez-vous les calculs):
Ici, nous voyons que l'équation converge - les sommes des masques des entrées et des sorties dont nous avons besoin sont les mêmes. Pour ce faire, le portefeuille génère aléatoirement
x 1 , y 1 , y 2 et y 3 , et le
x 2 restant calcule de cette façon:
En utilisant ces masques, nous pouvons prouver à quiconque vérifie que nous ne générons pas plus de fonds que nous n'en dépensons sans révéler le montant. Original, non?
RingCT full
Dans les transactions RingCT complètes, la vérification du montant des transferts est un peu plus complexe. Dans ces transactions, le portefeuille ne recompose pas les engagements pour les entrées, mais utilise ceux calculés lors de leur génération. Dans ce cas, nous devons supposer que la différence dans les montants que nous obtenons n'est plus égale à zéro, mais plutôt:
Ici
z est la différence entre les masques des entrées et des sorties. Si nous considérons
zG comme une clé publique (ce qui est de facto), alors
z est une clé privée. Ainsi, nous connaissons les clés publiques et privées correspondantes. Ayant ces données, nous pouvons les utiliser dans la signature en anneau MLSAG avec les clés publiques des sorties de pétrissage:
Ainsi, une signature en anneau valide garantira que nous connaissons toutes les clés privées de l'une des colonnes, et nous ne pouvons connaître la clé privée dans la dernière ligne que si la transaction ne génère pas plus de fonds qu'elle n'en dépense. Soit dit en passant, voici la réponse à la question «pourquoi la différence dans les montants des engagements ne mène-t-elle pas à zéro» - si
zG = 0 , alors nous ouvrirons la colonne avec les résultats réels.
Mais comment le destinataire sait-il combien d'argent il lui a envoyé? Ici, tout est simple: l'expéditeur de la transaction et les clés d'échange du destinataire en utilisant le protocole Diffie-Hellman, en utilisant la clé de transaction et la clé de vue du destinataire, et en calculant le secret partagé. L'expéditeur écrit dans les champs spéciaux des données de transaction les sommes des sorties chiffrées avec cette clé partagée.
Preuves de portée
Mais que se passe-t-il si vous utilisez un nombre négatif comme montant des engagements? Cela peut conduire à la génération de pièces supplémentaires! Un tel résultat est inacceptable, par conséquent, nous avons besoin d'une garantie que les montants que nous utilisons ne sont pas négatifs (sans divulguer ces montants, bien sûr, sinon c'est tellement de travail et tout cela en vain). En d'autres termes, nous devons prouver que la somme est dans l'intervalle
[0, 2 n - 1] .
Pour cela, la somme de chaque sortie est divisée en chiffres binaires et l'engagement pour chaque chiffre est considéré séparément. Comment cela se produit, il vaut mieux considérer un exemple.
Supposons que nous ayons de petites quantités et que nous nous adaptions à 4 bits (en pratique, c'est 64 bits), et nous créons une sortie pour la quantité de 5 XMR. Nous considérons des engagements pour chaque catégorie et un engagement général pour le montant total:
De plus, chaque engagement est mélangé à un substitut
(C i -2 i H) et est signé par paires par la signature de la bague Borromeo (une autre signature de l'anneau) proposée par Greg Maxwell en 2015 (plus d'informations à ce sujet
ici ):
Ensemble, cela s'appelle la preuve de fourchette et garantit que les engagements utilisent des montants dans l'intervalle
[0, 2 n - 1] .
Et ensuite?
Dans l'implémentation actuelle, les preuves de plage prennent beaucoup de place - 6 176 octets par sortie. Cela entraîne des transactions importantes et, par conséquent, des commissions plus élevées. Pour réduire la taille des transactions de Monero, les développeurs introduisent au lieu des signatures pare-balles Borromeo - un mécanisme à l'épreuve des plages sans engagements au niveau du bit.
Selon certaines estimations , ils peuvent réduire la taille d'épreuve à 94%. À propos, à la mi-juillet, la technologie a été
auditée par Kudelski Security, qui n'a pas révélé de lacunes importantes dans la technologie elle-même ou dans sa mise en œuvre. La technologie est déjà utilisée dans le réseau de test et avec le nouveau hard fork, elle peut probablement se déplacer vers le réseau principal.
Posez vos questions, proposez des sujets pour de nouveaux articles sur les technologies de crypto-monnaie et abonnez-vous à notre groupe sur
Facebook pour rester au courant de nos événements et publications.