Geekly articles weekly

Trier par sélection



Quelle est l'idée de trier par choix?

  1. Dans un sous-tableau non trié, un maximum local (minimum) est recherché.
  2. Le maximum (minimum) trouvé change de place avec le dernier (premier) élément du sous-tableau.
  3. Si des sous-réseaux non triés restent dans le tableau, voir le point 1.

Une légère digression lyrique. Dans un premier temps, dans ma série d'articles, j'avais prévu de présenter de manière cohérente des informations sur les classes de tri dans un ordre strict. Après le tri en bibliothèque , des articles sur d'autres algorithmes d'insertion étaient prévus: tri solitaire, tri par table Young, tri par inversion, etc.

Cependant, maintenant la tendance est à la non-linéarité, donc, sans écrire toutes les publications sur le tri par encarts, je vais commencer aujourd'hui une branche parallèle sur le tri par sélection. Ensuite, je ferai de même pour les autres classes algorithmiques: tris de fusion, tris de distribution, etc. Cela permettra généralement de rédiger des publications sur un sujet, puis sur un autre. Avec une telle rotation thématique, ce sera plus amusant.

Tri de sélection




Simple et sans prétention - nous parcourons le tableau à la recherche de l'élément maximum. Le maximum trouvé est échangé avec le dernier élément. La partie non triée du tableau a diminué d'un élément (n'inclut pas le dernier élément où nous avons réorganisé le maximum trouvé). Nous appliquons les mêmes actions à cette partie non triée - nous trouvons le maximum et le mettons à la dernière place dans la partie non triée du tableau. Et ainsi nous continuons jusqu'à ce que la partie non triée du tableau soit réduite à un élément.

def selection(data): for i, e in enumerate(data): mn = min(range(i, len(data)), key=data.__getitem__) data[i], data[mn] = data[mn], e return data


Le tri avec un choix simple est une double recherche approximative. Peut-il être amélioré? Regardons quelques modifications.

Tri double sélection :: Tri double sélection




Une idée similaire est utilisée dans le tri par shaker , qui est une variante du tri à bulles. En passant par la partie non triée du tableau, en plus du maximum, nous trouvons également simultanément le minimum. Nous mettons le minimum en premier lieu, le maximum en dernier. Ainsi, la partie non triée à chaque itération est réduite de deux éléments à la fois.

À première vue, il semble que cela accélère l'algorithme de 2 fois - après chaque passage, le sous-tableau non trié est réduit non pas d'un, mais de deux côtés à la fois. Mais en même temps, le nombre de comparaisons a augmenté de 2 fois et le nombre de swaps est resté inchangé. La double sélection n'augmente que légèrement la vitesse de l'algorithme et, dans certaines langues, il fonctionne même plus lentement pour une raison quelconque.

La différence entre le tri par choix et le tri par insertion


Il peut sembler que le tri par sélection et le tri par insertions sont une seule et même chose, une classe courante d'algorithmes. Eh bien, ou le tri par insertions est une sorte de tri par choix. Ou le tri par choix est un cas particulier de tri par insertions. Et ici et là, nous alternons la partie non triée du tableau pour extraire les éléments et les rediriger vers la zone triée.

La principale différence: dans le tri par insertions, nous extrayons tout élément de la partie non triée du tableau et l'insérons à sa place dans la partie triée. Dans le tri par sélection, nous recherchons délibérément l'élément maximum (ou minimum) avec lequel nous complétons la partie triée du tableau. Dans les encarts, nous cherchons où insérer l'élément suivant, et dans le choix - nous savons déjà à l'avance quelle place nous allons mettre, mais en même temps nous devons trouver l'élément qui correspond à cet endroit.

Cela rend les deux classes d'algorithmes complètement différentes les unes des autres dans leur essence et les méthodes utilisées.

Tri Bingo :: Tri Bingo


Une caractéristique intéressante des choix de tri est l'indépendance de vitesse de la nature des données triées.

Par exemple, si le tableau est presque trié, alors, comme vous le savez, le tri par insertions le traitera beaucoup plus rapidement (encore plus rapidement que le tri rapide). Un tableau en ordre inverse pour le tri par insertions est un cas dégénéré, il le triera le plus longtemps possible.

Et pour le tri par sélection, l'ordre partiel ou inverse du tableau ne joue pas de rôle - il le traitera à peu près à la même vitesse qu'un aléatoire normal. De plus, pour le tri classique, peu importe si le tableau est composé d'éléments uniques ou répétitifs - cela n'affecte pratiquement pas la vitesse.

Mais en principe, vous pouvez concevoir et modifier l'algorithme afin qu'il fonctionne plus rapidement avec certains ensembles de données. Par exemple, le tri bingo prend en compte si le tableau est composé d'éléments répétitifs.



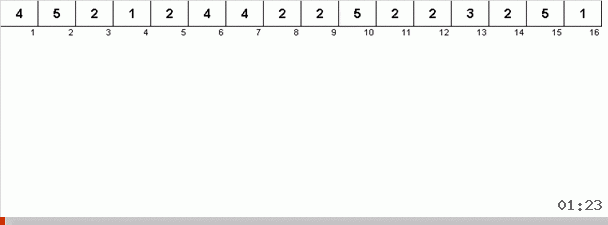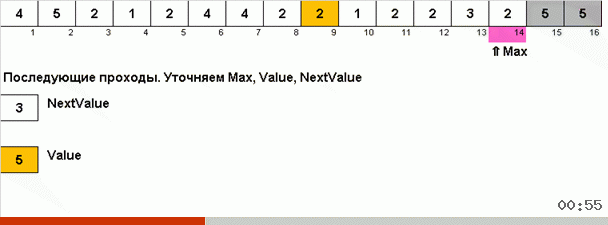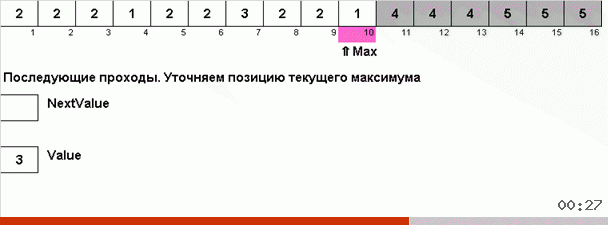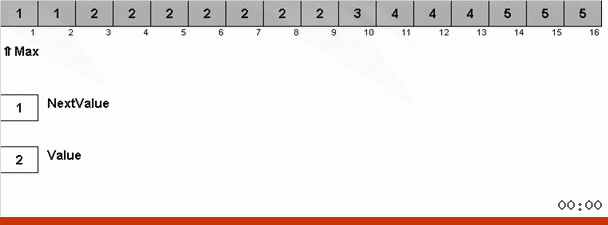
L'astuce ici est que non seulement l'élément maximum est mémorisé dans la partie désordonnée, mais aussi le maximum pour la prochaine itération est déterminé. Cela permet à des maxima répétés de ne pas les rechercher à chaque fois, mais de les remettre à leur place dès que ce maximum est à nouveau rencontré dans le tableau.

La complexité algorithmique est restée la même. Mais si le tableau consiste à répéter des nombres, le tri du bingo sera dix fois plus rapide que le tri normal par choix.

 # - def bingo(data): #  . max = len(data) - 1 nextValue = data[max] for i in range(max - 1, -1, -1): if data[i] > nextValue: nextValue = data[i] while max and data[max] == nextValue: max -= 1 #  . while max: value = nextValue nextValue = data[max] for i in range(max - 1, -1, -1): if data[i] == value: data[i], data[max] = data[max], data[i] max -= 1 elif data[i] > nextValue: nextValue = data[i] while max and data[max] == nextValue: max -= 1 return data


Tri par cycle :: Tri par cycle


Le tri en boucle est intéressant (et utile d'un point de vue pratique) en ce sens que les changements entre les éléments du tableau se produisent si et seulement si l'élément est mis à sa place finale. Cela peut être utile si la réécriture dans un tableau est trop coûteuse et que la gestion de la mémoire physique nécessite de minimiser le nombre de modifications apportées aux éléments du tableau.



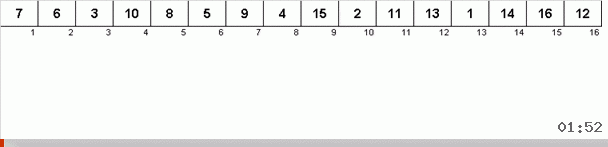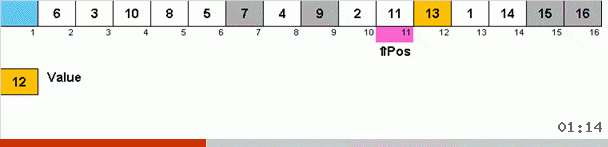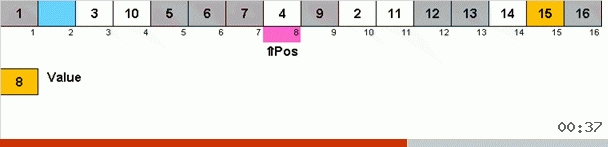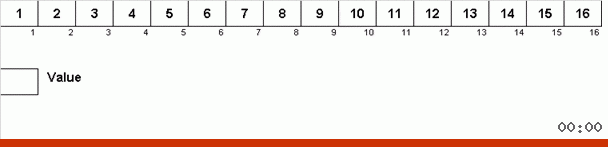
Cela fonctionne comme ça. Nous trions le tableau, appelons X la cellule suivante de cette boucle externe. Et nous regardons à quelle place dans le tableau nous devons insérer l'élément suivant de cette cellule. À l'endroit où vous souhaitez coller un autre élément, nous l'envoyons dans le presse-papiers. Pour cet élément dans le tampon, nous recherchons également sa place dans le tableau (et le collons à cet endroit, et envoyons au tampon l'élément qui apparaît à cet endroit). Et pour le nouveau numéro dans le tampon, nous effectuons les mêmes actions. Combien de temps ce processus devrait-il se poursuivre? Jusqu'à ce que l'élément suivant dans le presse-papiers se révèle être l'élément qui doit être inséré précisément dans la cellule X (l'emplacement actuel dans le tableau dans la boucle principale de l'algorithme). Tôt ou tard, ce moment se produira, puis dans la boucle externe, vous pouvez passer à la cellule suivante et répéter la même procédure pour cela.

Dans d'autres sortes, par choix, nous recherchons le maximum / minimum pour les mettre en dernière / première place. Dans le tri par cycle, il s'avère qu'au moins la première place dans le sous-tableau est située, pour ainsi dire, dans le processus de mise en place de plusieurs autres éléments quelque part au milieu du tableau.

Et ici, la complexité algorithmique reste également dans O ( n 2 ). Dans la pratique, le tri cyclique fonctionne même plusieurs fois plus lentement que le tri régulier par choix, car vous devez parcourir le tableau plus et comparer plus souvent. Il s'agit du prix pour le plus petit nombre possible de réécritures.

 #   def cycle(data): #        for cycleStart in range(0, len(data) - 1): value = data[cycleStart] # ,    pos = cycleStart for i in range(cycleStart + 1, len(data)): if data[i] < value: pos += 1 #      ,   #      if pos == cycleStart: continue #   ,     #        while value == data[pos]: pos += 1 data[pos], value = value, data[pos] #      , #         while pos != cycleStart: # ,    pos = cycleStart for i in range(cycleStart + 1, len(data)): if data[i] < value: pos += 1 #      #      while value == data[pos]: pos += 1 data[pos], value = value, data[pos] return data


Tri des crêpes


Un algorithme qui maîtrise tous les niveaux de vie - des bactéries à Bill Gates .



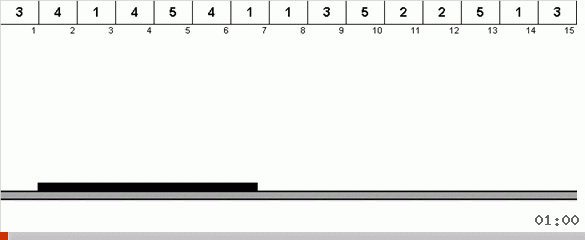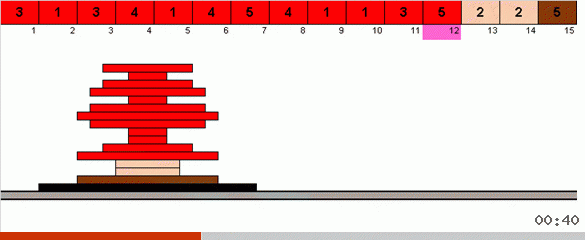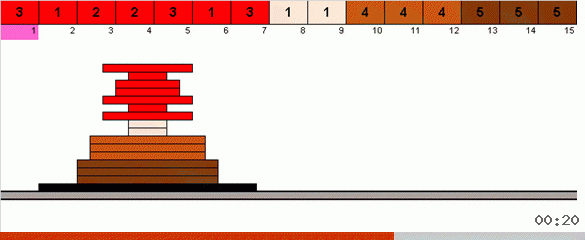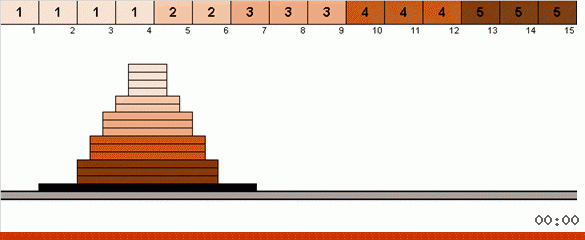
Dans le cas le plus simple, nous recherchons l'élément maximum dans la partie non triée du tableau. Lorsque le maximum est atteint, nous effectuons deux virages serrés. Tout d'abord, nous tournons la chaîne d'éléments de sorte que le maximum soit à l'extrémité opposée. Ensuite, nous retournons la totalité du sous-tableau non trié, à la suite de quoi le maximum se met en place.

De tels cordillets conduisent généralement à une complexité algorithmique en O ( n 3 ). Ces ciliés entraînés dégringolent d'un seul coup (par conséquent, dans leur exécution, la complexité est O ( n 2 )), et lors de la programmation, l'inversion d'une partie du réseau est un cycle supplémentaire.

Le tri des crêpes est très intéressant d'un point de vue mathématique (les meilleurs esprits pensaient à évaluer le nombre minimum de flips suffisants pour le tri), il existe des formulations plus complexes du problème (avec ce que l'on appelle un côté grillé). Le sujet des crêpes est extrêmement intéressant, j'écrirai peut-être une monographie plus complète sur ces questions.

 #   def pancake(data): if len(data) > 1: for size in range(len(data), 1, -1): #      maxindex = max(range(size), key = data.__getitem__) if maxindex + 1 != size: #    ,    if maxindex != 0: #  , #     data[:maxindex+1] = reversed(data[:maxindex+1]) #    , #      data[:size] = reversed(data[:size]) return data



Le tri de la sélection est aussi efficace que la recherche de l'élément minimum / maximum dans la partie non triée du tableau est organisée. Dans tous les algorithmes analysés aujourd'hui, la recherche s'effectue sous forme de double recherche. Et en double recherche, quoi qu'on en dise, la complexité algorithmique ne sera pas toujours meilleure que O ( n 2 ). Est-ce à dire que tous les triages par choix sont voués à signifier une complexité carrée? Pas du tout, si le processus de recherche est organisé d'une manière fondamentalement différente. Par exemple, considérez un ensemble de données comme un tas et recherchez sur le tas. Cependant, le sujet des tas n'est même pas un article, mais une saga entière, nous parlerons certainement de tas, mais une autre fois.

Les références


Sélection / Cycle , Crêpe / Crêpes

Articles de série:



Le bingo, le cycle et les crêpes d'aujourd'hui ont été ajoutés à l'application AlgoLab. Dans ce dernier, en rapport avec le dessin des crêpes, une restriction a été placée - les valeurs des éléments du tableau doivent être de 1 à 5. Vous pouvez bien sûr en mettre plus, mais les macros prendront au hasard des nombres de cette plage.

Source: https://habr.com/ru/post/fr422085/

More articles:


All Articles