Richard Hamming: Chapitre 13. Théorie de l'information

Nous l'avons fait!

«Le but de ce cours est de vous préparer à votre avenir technique.»

Salut, Habr. Vous vous souvenez de l'article génial «Vous et votre travail» (+219, 2588 signets, 429k lectures)?

Hamming (oui, oui, les codes Hamming à vérification automatique et à correction automatique) a un livre entier écrit sur la base de ses conférences. Nous le traduisons, parce que l'homme parle d'affaires.

Ce livre n'est pas seulement sur l'informatique, c'est un livre sur le style de pensée des gens incroyablement cool. «Ce n'est pas seulement une charge de pensée positive; il décrit les conditions qui augmentent les chances de faire du bon travail. »

Merci pour la traduction à Andrei Pakhomov.

La théorie de l'information a été développée par C.E.Shannon à la fin des années 40. La direction des Bell Labs a insisté pour l'appeler «théorie de la communication», car c'est un nom beaucoup plus précis. Pour des raisons évidentes, le nom "Théorie de l'information" a un impact beaucoup plus important sur le public, alors Shannon l'a choisi, et c'est ce que nous savons à ce jour. Le nom lui-même suggère que la théorie traite de l'information, ce qui la rend importante, car nous pénétrons plus profondément dans l'ère de l'information. Dans ce chapitre, je vais aborder quelques conclusions de base de cette théorie, je donnerai des preuves non pas strictes, mais plutôt intuitives de certaines des dispositions distinctes de cette théorie, afin que vous compreniez ce qu'est la "théorie de l'information", où vous pouvez l'appliquer et où pas .

Tout d'abord, qu'est-ce que «l'information»? Shannon identifie les informations avec incertitude. Il a choisi le logarithme négatif de la probabilité d'un événement comme mesure quantitative des informations que vous recevez lorsqu'un événement se produit avec une probabilité p. Par exemple, si je vous dis que le temps à Los Angeles est brumeux, alors p est proche de 1, ce qui dans l'ensemble ne nous donne pas beaucoup d'informations. Mais si je dis qu'il pleut à Monterey en juin, il y aura de l'incertitude dans ce message, et il contiendra plus d'informations. Un événement fiable ne contient aucune information, car log 1 = 0.

Arrêtons-nous là-dessus plus en détail. Shannon estimait qu'une mesure quantitative de l'information devrait être une fonction continue de la probabilité d'un événement p, et pour les événements indépendants, elle devrait être additive - la quantité d'informations obtenues à la suite de deux événements indépendants devrait être égale à la quantité d'informations obtenues à la suite d'un événement conjoint. Par exemple, le résultat d'un lancer de dés et de pièces est généralement considéré comme un événement indépendant. Traduisons ce qui précède dans le langage des mathématiques. Si I (p) est la quantité d'informations contenues dans l'événement avec probabilité p, alors pour un événement conjoint composé de deux événements indépendants x avec probabilité p ₁ et y avec probabilité p _2, nous obtenons


(événements indépendants x et y)

Il s'agit de l'équation fonctionnelle de Cauchy, vraie pour tous les p ₁ et p2. Pour résoudre cette équation fonctionnelle, supposons que

p ₁ = p ₂ = p,

ça donne



Si p ₁ = p ² et p ₂ = p, alors



etc. En étendant ce processus en utilisant la méthode standard pour les exponentielles pour tous les nombres rationnels m / n, ce qui suit est vrai



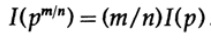
De la continuité supposée de la mesure d'information, il s'ensuit que la fonction logarithmique est la seule solution continue à l'équation fonctionnelle de Cauchy.

Dans la théorie de l'information, il est habituel de prendre la base du logarithme de 2, donc le choix binaire contient exactement 1 bit d'information. Par conséquent, les informations sont mesurées par la formule



Arrêtons-nous et voyons ce qui s'est passé ci-dessus. Tout d'abord, nous n'avons pas donné de définition à la notion d '«information», nous avons juste défini une formule pour sa mesure quantitative.

Deuxièmement, cette mesure dépend de l'incertitude, et bien qu'elle soit suffisamment adaptée aux machines - par exemple, les systèmes téléphoniques, la radio, la télévision, les ordinateurs, etc. - elle ne reflète pas une attitude humaine normale à l'égard de l'information.

Troisièmement, il s'agit d'une mesure relative, elle dépend de l'état actuel de vos connaissances. Si vous regardez le flux de «nombres aléatoires» du générateur de nombres aléatoires, vous supposez que chaque nombre suivant est indéfini, mais si vous connaissez la formule de calcul des «nombres aléatoires», le nombre suivant sera connu et, par conséquent, ne contiendra pas informations.

Ainsi, la définition donnée par Shannon pour l'information convient dans de nombreux cas aux machines, mais ne semble pas correspondre à la compréhension humaine du mot. Pour cette raison, la «théorie de l'information» devrait être appelée «théorie de la communication». Cependant, il est trop tard pour changer les définitions (grâce à quoi la théorie a gagné sa popularité initiale, et qui font encore penser que cette théorie traite de «l'information»), donc nous devons les accepter, mais vous devez comprendre clairement à quel point la définition des informations donnée par Shannon est loin de son bon sens. Les informations de Shannon portent sur quelque chose de complètement différent, à savoir l'incertitude.

C'est à cela que vous devez penser lorsque vous proposez une terminologie. Dans quelle mesure la définition proposée, par exemple, la définition donnée par Shannon, avec votre idée originale, et en quoi est-elle différente? Il n'y a presque pas de terme qui refléterait fidèlement votre vision antérieure du concept, mais en fin de compte, c'est la terminologie utilisée qui reflète le sens du concept, donc formaliser quelque chose à travers des définitions claires fait toujours du bruit.

Considérons un système dont l'alphabet est composé de symboles q avec des probabilités pi. Dans ce cas, la quantité moyenne d'informations dans le système (sa valeur attendue) est:



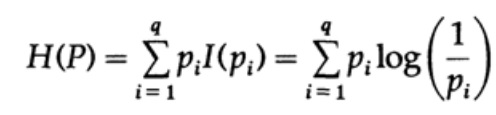
C'est ce qu'on appelle l'entropie du système de distribution de probabilité {pi}. Nous utilisons le terme «entropie» car la même forme mathématique se pose en thermodynamique et en mécanique statistique. C'est pourquoi le terme «entropie» crée autour de lui une aura d'importance qui, finalement, n'est pas justifiée. La même forme mathématique de notation n'implique pas la même interprétation des caractères!

L'entropie de la distribution de probabilité joue un rôle majeur dans la théorie du codage. L'inégalité de Gibbs pour deux distributions de probabilité différentes pi et qi est l'une des conséquences importantes de cette théorie. Nous devons donc prouver que



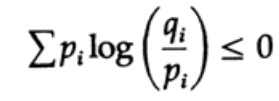
La preuve est basée sur un graphique évident, fig. 13.I, qui montre que



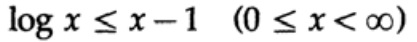
et l'égalité n'est atteinte que pour x = 1. Nous appliquons l'inégalité à chaque somme de la somme du côté gauche:



Si l'alphabet du système de communication se compose de q caractères, puis en prenant la probabilité de transmission de chaque caractère qi = 1 / q et en substituant q, nous obtenons de l'inégalité de Gibbs





Figure 13.I

Cela suggère que si la probabilité de transmettre tous les q caractères est la même et égale à - 1 / q, alors l'entropie maximale est ln q, sinon l'inégalité tient.

Dans le cas d'un code uniquement décodé, nous avons l'inégalité Kraft



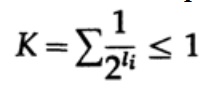
Maintenant, si nous définissons des pseudo-probabilités



où bien sûr = 1, qui découle de l'inégalité de Gibbs,



et appliquer une algèbre (rappelez-vous que K ≤ 1, afin que nous puissions omettre le terme logarithmique, et éventuellement renforcer l'inégalité plus tard), nous obtenons



où L est la longueur moyenne du code.

Ainsi, l'entropie est la limite minimale pour tout code de caractère avec un mot de code moyen L. C'est le théorème de Shannon pour un canal sans interférence.

Nous considérons maintenant le théorème principal sur les limites des systèmes de communication dans lesquels l'information est transmise sous la forme d'un flux de bits indépendants et du bruit est présent. On suppose que la probabilité de transmission correcte d'un bit est P> 1/2, et la probabilité que la valeur du bit soit inversée pendant la transmission (une erreur se produit) est Q = 1 - P. Pour plus de commodité, nous supposons que les erreurs sont indépendantes et la probabilité d'erreur est la même pour chaque envoyé bits - c'est-à-dire qu'il y a du «bruit blanc» dans le canal de communication.

La façon dont nous avons un long flux de n bits codés dans un seul message est une extension à n dimensions d'un code à un bit. Nous déterminerons la valeur de n plus tard. Considérons un message composé de n bits comme un point dans un espace à n dimensions. Comme nous avons un espace à n dimensions - et pour simplifier, nous supposons que chaque message a la même probabilité d'occurrence - il y a M messages possibles (M sera également déterminé plus tard), par conséquent, la probabilité de tout message envoyé est égale à




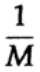
(expéditeur)
Graphique 13.II

Ensuite, considérez l'idée de la bande passante du canal. Sans entrer dans les détails, la capacité du canal est définie comme la quantité maximale d'informations pouvant être transmise de manière fiable sur le canal de communication, en tenant compte de l'utilisation du codage le plus efficace. Il n'y a aucun argument selon lequel plus d'informations peuvent être transmises par le canal de communication que sa capacité. Cela peut être prouvé pour un canal symétrique binaire (que nous utilisons dans notre cas). La capacité du canal pour l'envoi au niveau du bit est définie comme



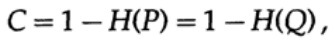
où, comme précédemment, P est la probabilité d'absence d'erreur dans un bit envoyé. Lors de l'envoi de n bits indépendants, la capacité du canal est déterminée comme



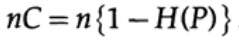
Si nous sommes proches de la bande passante du canal, alors nous devrions envoyer presque un tel volume d'informations pour chacun des caractères ai, i = 1, ..., M. Étant donné que la probabilité d'occurrence de chaque caractère ai est 1 / M, nous obtenons



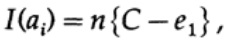
lorsque nous envoyons l'un des M messages équiprobables ai, nous avons



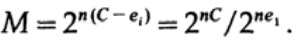
Lors de l'envoi de n bits, nous nous attendons à ce que des erreurs nQ se produisent. En pratique, pour un message composé de n bits, nous aurons environ nQ erreurs dans le message reçu. Pour n grand, variation relative (variation = largeur de distribution,)
la distribution du nombre d'erreurs sera plus étroite avec l'augmentation de n.

Donc, du côté de l'émetteur, je prends le message ai pour envoyer et dessiner une sphère autour d'elle avec un rayon



qui est légèrement plus grand d'un montant égal à e2 que le nombre d'erreurs Q attendu (figure 13.II). Si n est suffisamment grand, il existe alors une probabilité arbitrairement faible d'apparition du point de message bj du côté récepteur, qui va au-delà de cette sphère. Nous allons dessiner la situation, telle que je la vois du point de vue de l'émetteur: nous avons tous les rayons du message transmis ai au message reçu bj avec une probabilité d'erreur égale (ou presque égale) à la distribution normale, atteignant un maximum en nQ. Pour tout e2 donné, il y a n si grand que la probabilité que le point résultant bj, dépassant ma sphère, soit aussi petit que vous le souhaitez.

Considérez maintenant la même situation de votre part (Fig. 13.III). Du côté récepteur, il y a une sphère S (r) de même rayon r autour du point reçu bj dans l'espace à n dimensions, de sorte que si le message reçu bj est à l'intérieur de ma sphère, alors le message ai que j'ai envoyé est à l'intérieur de votre sphère.

Comment une erreur peut-elle se produire? Une erreur peut se produire dans les cas décrits dans le tableau ci-dessous:



Figure 13.III



Ici, nous voyons que si dans la sphère construite autour du point reçu, il y a au moins un point correspondant à un éventuel message non codé envoyé, alors une erreur s'est produite lors de la transmission, car vous ne pouvez pas déterminer lequel de ces messages a été transmis. Le message envoyé ne contient pas d'erreurs uniquement si le point qui lui correspond est dans la sphère, et il n'y a pas d'autres points possibles dans ce code qui se trouvent dans la même sphère.

Nous avons une équation mathématique pour la probabilité d'une erreur Re si ai a été envoyé



On peut jeter le premier facteur dans le second terme, en le prenant comme 1. Ainsi, on obtient l'inégalité



De toute évidence,



donc



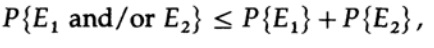
présenter une nouvelle demande au dernier membre à droite



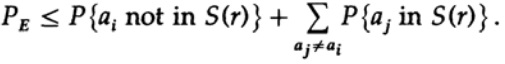
Si n est pris assez grand, le premier terme peut être pris arbitrairement petit, disons inférieur à un certain nombre d. Nous avons donc



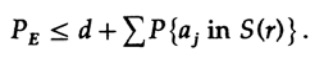
Voyons maintenant comment vous pouvez créer un code de remplacement simple pour coder M messages composés de n bits. N'ayant aucune idée de comment construire le code (les codes de correction d'erreur n'ont pas encore été inventés), Shannon a choisi le codage aléatoire. Lancez une pièce pour chacun des n bits du message et répétez le processus pour M messages. Tout ce que vous avez à faire est de lancer des pièces nM, donc c'est possible



dictionnaires de code ayant la même probabilité de ½nM. Bien sûr, le processus aléatoire de création d'un livre de codes signifie qu'il existe une probabilité de doublons, ainsi que des points de code, qui seront proches les uns des autres et, par conséquent, seront une source d'erreurs probables. Il est nécessaire de prouver que si cela ne se produit pas avec une probabilité supérieure à tout petit niveau d'erreur sélectionné, alors le n donné est suffisamment grand.
Le point décisif est que Shannon a fait la moyenne de tous les livres de codes possibles pour trouver l'erreur moyenne! Nous utiliserons le symbole Av [.] Pour désigner la moyenne sur l'ensemble de tous les dictionnaires de code aléatoire possibles. Une moyenne sur la constante d, bien sûr, donne une constante, car pour faire la moyenne chaque terme coïncide avec tout autre terme de la somme



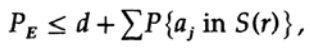
qui peut être augmenté (M - 1 passe à M)



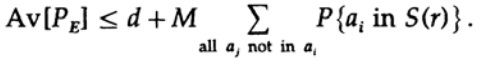
Pour tout message particulier, lors de la moyenne de tous les livres de codes, le codage passe par toutes les valeurs possibles, de sorte que la probabilité moyenne qu'un point se trouve dans une sphère est le rapport du volume de la sphère au volume total de l'espace. L'étendue de la sphère



où s = Q + e2 <1/2 et ns doit être un entier.

Le dernier terme à droite est le plus grand de cette somme. Premièrement, nous estimons sa valeur par la formule de Stirling pour les factorielles. Ensuite, nous regardons le coefficient de réduction du terme devant lui, notons que ce coefficient augmente en se déplaçant vers la gauche, et donc nous pouvons: (1) limiter la valeur de la somme à la somme de la progression géométrique avec ce coefficient initial, (2) étendre la progression géométrique de ns membres à nombre infini de termes, (3) calculer la somme de la progression géométrique infinie (algèbre standard, rien de significatif) et enfin obtenir la valeur limite (pour un n suffisamment grand):



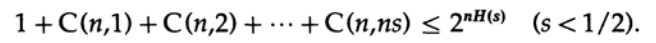
Remarquez comment l'entropie H (s) est apparue dans l'identité binomiale. Il est à noter que l'expansion dans la série de Taylor H (s) = H (Q + e2) donne une estimation obtenue en prenant en compte uniquement la dérivée première et en ignorant toutes les autres. Collectons maintenant l'expression finale:



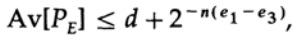
où



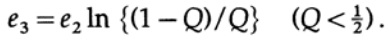
Il suffit de choisir e2 pour que e3 <e1, puis le dernier terme soit arbitrairement petit, pour n suffisamment grand. Par conséquent, l'erreur PE moyenne peut être obtenue arbitrairement petite avec une capacité de canal arbitrairement proche de C.
Si la moyenne de tous les codes a une erreur suffisamment faible, alors au moins un code doit être approprié, par conséquent, au moins un système de codage approprié existe. C'est un résultat important obtenu par Shannon - «Théorème de Shannon pour un canal avec interférence», même s'il convient de noter qu'il l'a prouvé pour un cas beaucoup plus général que pour un simple canal symétrique binaire que j'ai utilisé. Pour le cas général, les calculs mathématiques sont beaucoup plus compliqués, mais les idées ne sont pas si différentes, donc très souvent, en utilisant l'exemple d'un cas spécial, on peut révéler la vraie signification du théorème.

Critiquons le résultat. Nous avons répété à plusieurs reprises: "Pour un n suffisamment grand". Mais quelle est la taille de n? Très, très grand, si vous voulez vraiment être simultanément proche de la bande passante du canal et être sûr du bon transfert de données! Tellement gros qu'en fait, vous devrez attendre très longtemps pour accumuler un message à partir de tant de bits afin de le coder plus tard. Dans le même temps, la taille du dictionnaire de code aléatoire sera énorme (après tout, un tel dictionnaire ne peut pas être représenté sous une forme plus courte que la liste complète de tous les Mn bits, alors que n et M sont très grands)!

Les codes de correction d'erreurs évitent d'attendre un très long message, avec son encodage et son décodage ultérieurs via de très grands livres de codes, car ils évitent les livres de codes en soi et utilisent à la place des calculs conventionnels. Dans une théorie simple, ces codes perdent généralement leur capacité à approcher la capacité du canal et maintiennent en même temps un taux d'erreur assez faible, mais lorsque le code corrige un grand nombre d'erreurs, ils donnent de bons résultats. En d'autres termes, si vous disposez d'une certaine capacité de canal pour la correction d'erreurs, vous devez utiliser l'option de correction d'erreurs la plupart du temps, c'est-à-dire que dans chaque message envoyé, un grand nombre d'erreurs doit être corrigé, sinon vous perdez cette capacité en vain.

De plus, le théorème prouvé ci-dessus n'est toujours pas dénué de sens! Il montre que les systèmes de transmission efficaces devraient utiliser des schémas de codage sophistiqués pour les très longues chaînes de bits. Un exemple est les satellites qui ont volé en dehors de la planète extérieure; à mesure qu'ils s'éloignent de la Terre et du Soleil, ils sont obligés de corriger de plus en plus d'erreurs dans le bloc de données: certains satellites utilisent des batteries solaires, qui fournissent environ 5 watts, d'autres utilisent des sources d'énergie atomique qui fournissent à peu près la même puissance.La faible puissance de la source d'alimentation, la petite taille des plaques émettrices et la taille limitée des plaques réceptrices sur Terre, la distance énorme que le signal doit parcourir - tout cela nécessite l'utilisation de codes avec un niveau élevé de correction d'erreur pour construire un système de communication efficace.

n- , . , , , — , , , . , , nQ, . , , . , , , . n- , M . , , . , — , , .

, , . , , , , . , , , , . , , - , .

. , , , , , . , , , , , ; , , . , , .

IQ, , , . , , , . , , , , «» ( ). , , , . ? , , ? ! , , .

, , , , , . , , , , . , , . , , - .

, . , , , ! , .

...

, — magisterludi2016@yandex.ru

, — «The Dream Machine: » )

, , . ( 10 , 20 )