Puis le premier septembre, la prochaine année académique, des fleurs, des bonbons, des larmes de bonheur sont arrivées, et c'est tout, et en train de préparer la conférence à l'institut, je suis tombé sur des données très intéressantes. J'ai vu que cela pouvait être rapidement et magnifiquement dessiné dans GePhi , et je suis tombé sur l'histoire de Johannes Delitsch. Delich a travaillé à Leipzig en tant que professeur d'école primaire et a collecté des données sur les amis avec qui dans sa classe pendant l'année scolaire 1880. Et cela, en cours de route, est l'un des premiers graphiques sociaux documentés.

Les classes étaient alors grandes (il y avait déjà 53 élèves dans cette classe particulière), et le vieux Johannes, si je comprends bien, a travaillé comme tuteur jusqu'en 1880. Donc, au début de la nouvelle année scolaire, après avoir vu mon quatrième "A" (pour être honnête, je ne sais pas quelle était la lettre, ce n'est pas si important), Johannes s'est senti un peu triste. Apparemment, il était actif et a décidé de mieux comprendre les relations sociales de la foule qui lui était confiée.
Les données
Johannes n'était pas un sociologue moderne. Il était professeur d'école, donc sa méthodologie de collecte de données était jolie, ahem, éclectique. Il a parlé avec les élèves, a lu leurs devoirs et a "regardé comment ils communiquent en groupe". Le résultat a été un ensemble de données plutôt verdoyant sur la base duquel Delic a écrit un article dans Zeitschrift für.
Kinderforschung (tous les mots en allemand et sont très effrayants, désolés d'avance, mais la traduction littérale du "Journal pour l'étude des enfants" sonne encore plus effrayant en russe). Johannes, si j'ai bien compris, était principalement intéressé par la façon dont les performances de l'enfant et sa popularité sont liées aux camarades de classe.Par conséquent, en plus du graphique directionnel qui décrit qui il est ami, Delic donne également la note de l'élève (du plus réussi au plus infructueux) et certains options intéressantes. Par exemple, il y avait quatre élèves de deuxième année dans la classe, ils sont mis en évidence dans l'ensemble de données. Également dans la classe, il y avait un gars du nom de Lasch, dont la grand-mère était pâtissière. Delic a remarqué que Lash traite d'autres enfants avec des bonbons et l'a noté dans ses données. Il a également identifié séparément les enfants qui avaient des problèmes de santé, tels que l'anémie, la boiterie ou un retard de développement.
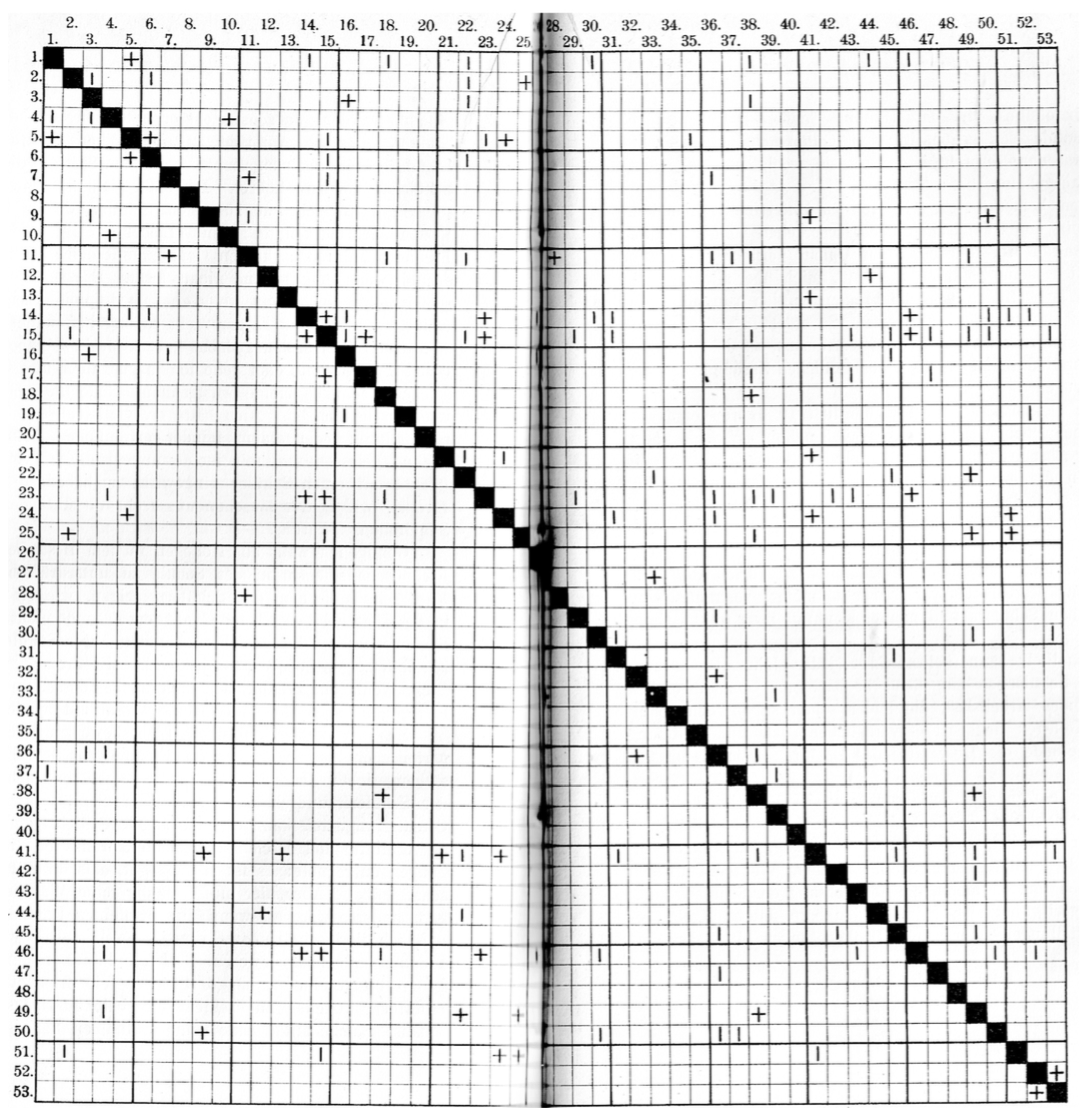
La «matrice de l'amitié» décrit qui est ami et avec qui. Le décompte est dirigé, car Hans peut considérer Frédéric comme un ami, et Frédéric, peut-être qu'il voulait éternuer contre Hans.
Les meilleures personnes de notre classe
Mettons ce graphique social dans GePhi, calculons, par exemple, PageRank et colorions les sommets.

Les élèves les plus «influents» sont peints dans une couleur plus saturée.
«Soulignons» les sept étudiants ayant le PageRank le plus élevé (j'expliquerai pourquoi exactement sept plus tard, pour l'instant, prenons simplement sept comme constante fondamentale). C'est ce qui se produit si vous sélectionnez sept sommets du graphique qui ont le PageRank le plus élevé.

Les leaders d'opinion du quatrième "A" en 1880.
Nous avons déjà parlé de ces gars! Premièrement, les quatre élèves de deuxième année sont «dans le haut». J'ai décidé de distinguer sept personnes, car l'un des quatre enfants de deuxième année du nom de Schnabel n'est pas très cool. Il a la septième valeur de PageRank. Alors que les étudiants de deuxième année Pheil et Vetter prennent en toute confiance (et avec une large marge) les première et deuxième lignes de la liste des "autorités", et les étudiants de deuxième année Schubert - la quatrième, juste derrière "l'autorité" Lasha (peu peut rivaliser) avec la distribution de bonbons). Schnabel est septième. L'autorité supérieure est le meilleur élève de la classe Schlegel et le cinquième élève le plus réussi de Meinhold. Nous ne savons rien de ce Maynhold, Delich ne nous a laissé aucune information particulière à son sujet, donc nous le désignerons comme un "gars étrange" sur la photo.
Battements de tambourin et calcul de la classe de modularité
GePhi dispose d'un outil pour trouver des groupes d'intérêt dans notre quatrième groupe «A». L'algorithme est décrit ici , et l'implémentation utilisée par GePhi est ici . L'idée générale est que l'algorithme essaie d'évaluer quelles communautés au sein du réseau sont plus denses. En quelques passes, l'algorithme peut donner une répartition différente en communautés, donc tout ce qui vient ensuite est simplement de lancer et de souffler un tambourin basé sur un seul résultat, ce qui ne rend pas le processus moins amusant. Ainsi, notre quatrième algorithme de recherche de communauté «A» a peint de telles couleurs.

Dites-moi avec qui vous êtes amis et je dirai que vous êtes en vain.
Voyons ce qui s'est passé. Tous nos sept gars les plus influents sont tombés dans quatre communautés principales. Trois «cool» toute l'année Pfail, Fetter et Schubert sont tombés dans la communauté, peints en vert sur la photo. Le Schnabel répétitif "Nekrutoy" et le meilleur élève de la classe Schlegel tombèrent dans une communauté peinte en violet. Enfin, Lash, le distributeur de bonbons, est tombé dans la communauté indiquée sur la photo en bleu clair. Meinhold reste un homme mystérieux. Il s'est retrouvé dans un petit groupe de «favoris», dans lequel il n'y a que trois étudiants (dont lui-même), elle est peinte en gris foncé. Sur les quatre enfants qui avaient des problèmes de santé, deux n'étaient amis avec personne et les deux autres tombaient dans la communauté bleue.
Eh bien. Beaucoup commence à s'éclaircir. Schnabel, apparemment, n'est pas une répétition aussi «cool», car au lieu de traîner avec des gars durs, il communique avec des nerds qui sont amis avec le copilote Schlegel (il est intéressant de noter que Schnabel et Schlegel eux-mêmes ne sont pas amis, mais de manière stable dans une communauté lors du calcul de la modularité du réseau). Lash et ses bonbons ont formé une communauté de gars qui ne sont ni des nerds ni des méchants, et Meinhold ... Hmmm ... Qui est Meinhold? Voyons qui d'autre est avec lui "dans une fête". Deux autres étudiants qui sont tombés dans la même communauté avec lui sont Mayer (Meier, quatrième dans le classement des étudiants) et Flash (Flasch, trente-cinquième dans le classement des étudiants). Hmmm ... Trois mecs qui ne communiquent plus vraiment avec personne, mais deux d'entre eux apprennent assez bien ...

Image du film Superbad.
En bref, j'aime à penser à ces trois gars comme une trinité de geeks de l'Allemagne du 19ème siècle. Deux d'entre eux étudient bien, et le troisième ne communique avec personne en particulier, il fait simplement un robot humanoïde géant ou une kriegsmarine après l'école, ou pire. Pas le point.
Traduisons la note des écoliers allemands en note moyenne. Nous allons générer quelque chose de similaire à la distribution normale dans la gamme de 2 à 5 (les Allemands ont une échelle de notation inverse, mais pour notre compréhension, nous ferons tout selon notre échelle habituelle, lorsque 2 ne passera pas et 5 est beau). Nous associons chaque élève à sa note moyenne de sorte que lors du classement selon cette note moyenne, la même note soit obtenue que dans les données de Delich. Voyons maintenant quel est le score moyen des élèves dans chacun de ces quatre groupes. Et en même temps, combien de personnes sont en moyenne membres de chaque groupe et combien de personnes sont en moyenne amicales avec lui. Le résultat est le suivant:
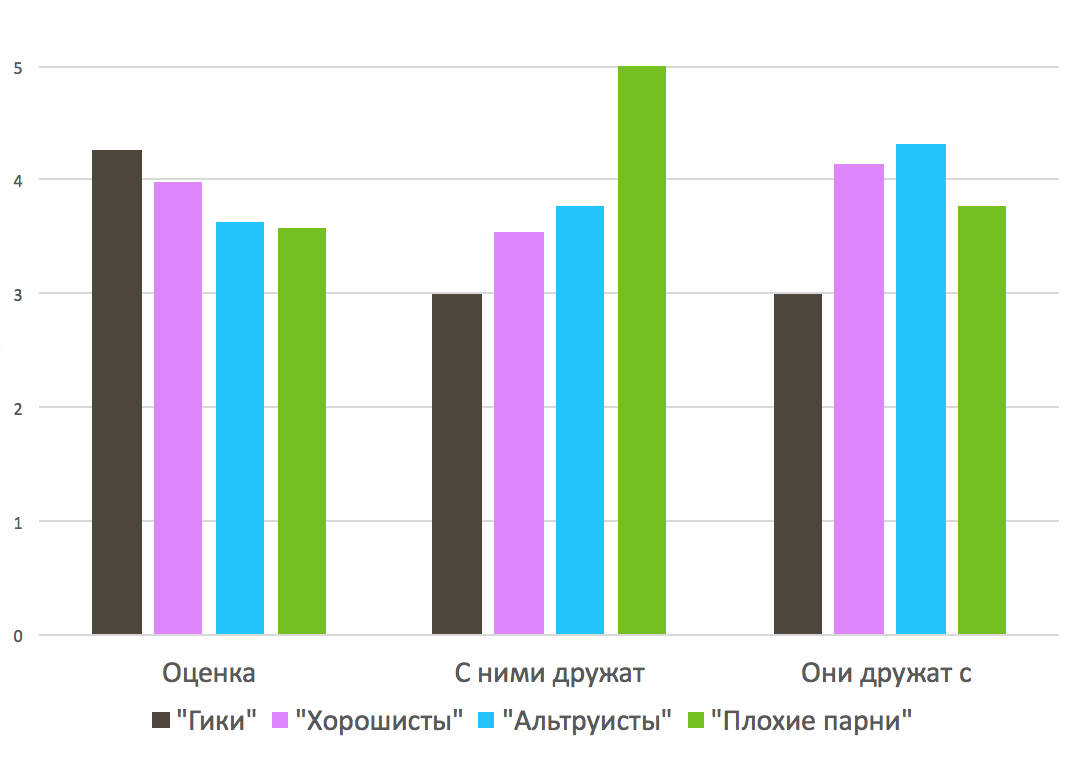
Le score moyen et le degré moyen d'entrée et de sortie pour quatre groupes. Les couleurs correspondent à la coloration du graphique.
Les geeks, en général, étudient bien, mais ils ne sont pas eux-mêmes désireux de se faire des amis, et personne ne sera ami avec eux non plus. Les bons savants du parti de Schlegel et Schnabel étudient en moyenne pire que les geeks, mais en termes sociaux, ils font mieux. Les altruistes (comme j'ai appelé le groupe dans lequel Lash distribuait des bonbons) étudient les moches mais sont les amis les plus actifs des autres enfants (mais pas mutuellement). Enfin, les méchants apprennent le pire, mais ils sont très populaires (ils veulent être amis avec eux), même s'ils ne sont pas loin des geeks en termes de nombre de personnes avec qui ils sont amis.
Dessinons avec qui les représentants des différentes communautés sont amis
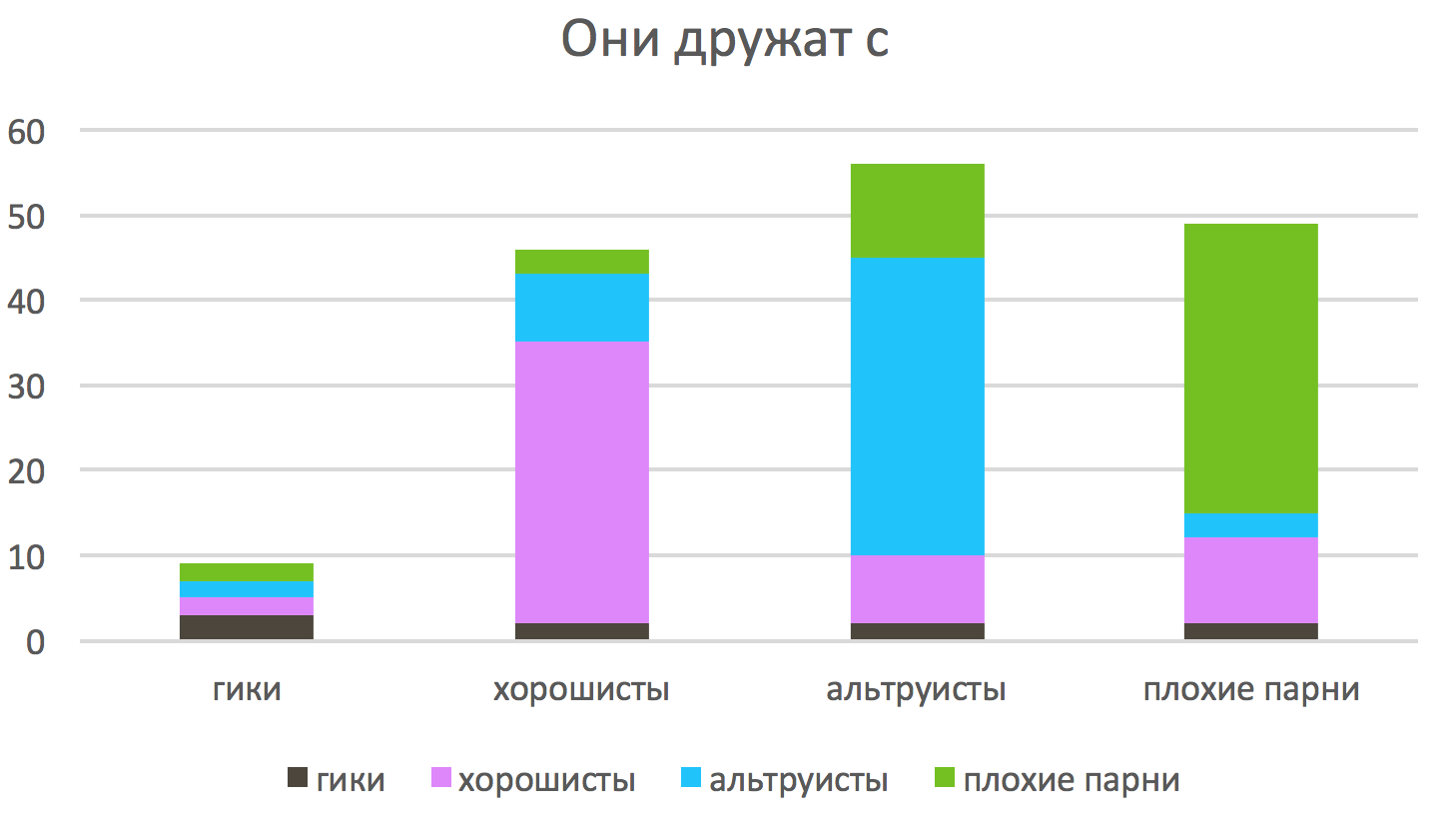
Chaque communauté est la plupart de ses amis en elle-même, mais interagit avec les autres communautés de différentes manières.
Voyez comme c'est drôle! Les altruistes considèrent leurs amis comme beaucoup de bons et beaucoup de méchants. Les méchants des altruistes ne sont pas particulièrement favorables, mais ici ils considèrent que certains bons sont leurs amis. Les bonnes personnes, à en juger par tout, ne sont pas satisfaites de l'amitié avec les méchants, mais les altruistes avec leurs visages souriants et leurs bonbons gratuits suscitent leur intérêt restreint.
Si pour une raison quelconque, vous êtes plus intéressé à regarder d'un autre côté, voici une autre photo de prix.

Chaque communauté est la plupart de ses amis en elle-même, mais interagit avec les autres communautés de différentes manières.
Voici un ensemble de données aussi drôle au cours de la première semaine de l'automne. En 2014, les données de notre quatrième «A» ont été redécouvertes par cet article . Le fait est qu'après la Première Guerre mondiale, l'Allemagne n'était pas à la hauteur de la pédagogie, de sorte que les données collectées par Delic ont été oubliées pendant longtemps, mais il s'avère maintenant que c'est presque le premier graphique social complètement documenté. De telles choses.
Les données originales ont été publiées dans l'article:
Delitsch, J., 1900. Über Schülerfreundschaften in einer Volksschule. Zeitschrift für Kinderforschung 5, 150-162.
PS On m'a demandé à plusieurs reprises de quel type de moralité il s'agit. Je pense que la morale est ici.
Premièrement, même quelques colonnes de chiffres peuvent masquer le drame. Oui, même quoi.
Deuxièmement, pour toute personne travaillant avec des données, la réponse à la question "quelle est la morale?" revient à la question "quelle est la métrique de qualité?"
Si la métrique est la performance académique, il vaut mieux être ami avec d'excellents élèves. Tous les étudiants de deuxième année, en fait, ne sont pas dans le haut de la classe, mais pas tout en bas en termes de performances académiques. Ils traînent quelque part au milieu, mais d'autres enfants de leur communauté apprennent bien pire. La performance relativement bonne des élèves de deuxième année est peut-être due au fait que l'école allemande du XIXe siècle a accordé beaucoup d'attention à l'entraînement physique et aux sports, de sorte que la «performance» des élèves de deuxième année est surestimée en raison du fait qu'ils sont simplement plus forts physiquement. La communauté autour de Schlegel et la communauté des geeks, malgré ce biais, étudient beaucoup mieux que la communauté qui se formait autour des étudiants de deuxième année.
Si la métrique est populaire parmi les pairs, la dispersion des bonbons est un moyen plutôt coûteux et peu efficace d'obtenir cette même popularité. D'une part, cela fonctionne: Lash est le troisième élève le plus populaire de la classe. En revanche, la «qualité» de sa communauté (par la métrique de popularité sociale) est plutôt faible. C'est-à-dire que les bonbons vous permettent de devenir populaire parmi les gens peu populaires. Les autres gars populaires de Lasha ne sont pas amis (ni redoublants, ni meilleur élève de la classe Schlegel).
Enfin, si la métrique est le nombre de «vrais» amis (où un vrai ami n'est pas une personne avec qui vous êtes amis, mais seulement ceux de vos amis qui sont amis avec vous), alors être un étudiant de deuxième année est juste cela.