Cachez-vous sans vous cacher. Encore une fois sur la stéganographie LSB, le chi carré et ... la singularité?

Aujourd'hui, nous allons à nouveau remonter l'ancien nid et parler de la façon de cacher un tas de bits dans l'image avec un chat, regarder plusieurs outils disponibles et analyser les attaques les plus populaires. Et il semblerait, qu'en est-il de la singularité?

Comme on dit, si vous voulez comprendre quelque chose, alors écrivez un article à ce sujet sur Habr! (Attention, beaucoup de texte et d'images)



La stéganographie (littéralement de la «cryptographie» grecque) est la science de la transmission de données cachées (messages stego) dans d'autres données ouvertes (stegocontainers) tout en cachant le fait même du transfert de données. Ne vous inquiétez pas, en fait, tout n'est pas si compliqué.

Alors, où dans l'image pouvez-vous cacher le message pour que personne ne le remarque?

Et il n'y a que deux endroits: les métadonnées et l'image elle-même. Ce dernier est assez simple, il suffit de taper «exif» sur Google. Commençons donc tout de suite avec le second.

Bit le moins significatif

Le modèle de couleur le plus populaire est RVB, où la couleur est représentée sous la forme de trois composants: rouge, vert et bleu . Chaque composant est codé dans la version classique en utilisant 8 bits, c'est-à-dire qu'il peut prendre une valeur de 0
à 255. C'est ici que se cache le bit le moins significatif. Il est important de comprendre qu'une telle couleur RVB représente trois de ces bits.

Pour les présenter plus clairement, nous allons faire quelques petites manipulations.

Comme promis, prenez une photo d'un chat au format png.



Nous le divisons en trois canaux et dans chaque canal, nous prenons le bit le moins significatif. Créez trois nouvelles images, où chaque pixel représente NZB. Zéro - le pixel est blanc, l'unité est respectivement noire.

Nous obtenons cela.




Mais, en règle générale, l'image se trouve sous la «forme assemblée». Pour représenter le NZB des trois composants dans une image, il suffit de remplacer le composant dans un pixel où le NZB est l'unité, de le remplacer par 255 et sinon de le remplacer par 0.

Mais pas moins important

Imaginez que tout ce que nous avons vu dans la dernière photo nous appartient et que nous avons le droit d'en faire quoi que ce soit. Ensuite, nous le prenons comme un flux de bits, d'où nous pouvons lire et où nous pouvons écrire.

Nous prenons les données que nous voulons intercaler dans l'image, les présentons sous forme de bits et les notons à la place de celles existantes.

Pour extraire ces données, nous lisons le NZB en tant que flux binaire et le mettons sous la forme souhaitée. Pour savoir combien de bits doivent être comptés, en règle générale, la taille du message est écrite au début. Mais ce sont des détails d'implémentation.

Il convient de noter que dans environ 50% des cas, le bit que nous voulons écrire et le bit dans l'image coïncideront et nous n'aurons rien à changer.

C'est tout, la méthode se termine ici.

Pourquoi ça marche?

Jetez un œil aux images ci-dessous.

Ceci est un stegocontainer vide:



Et c'est plein à 95%:



Tu vois la différence? Mais elle l'est. Pourquoi

Examinons deux couleurs: (0, 0, 0) et (1, 1, 1), c'est-à-dire des couleurs différentes uniquement par le NZB dans chaque composant.



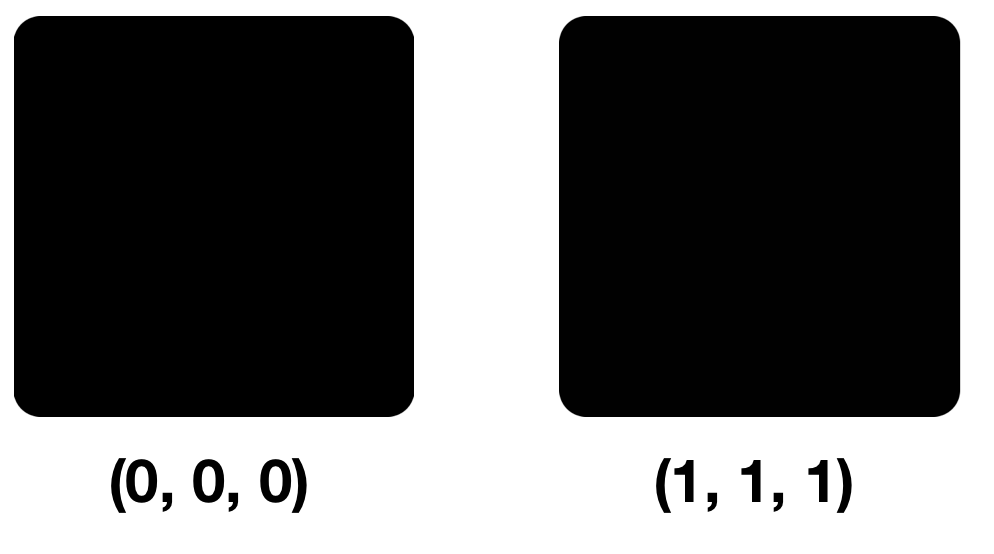
De légères différences de pixels au premier, deuxième et troisième coup d'œil ne seront pas perceptibles. Le fait est que notre œil peut distinguer environ 10 millions de couleurs et le cerveau seulement 150. Le modèle RVB contient également 16 777 216 couleurs. Vous pouvez essayer de les distinguer tous ici.

Depuis la ligne de commande

Il n'y a pas beaucoup d'outils de ligne de commande open source disponibles qui représentent la stéganographie LSB.

Les plus populaires se trouvent dans le tableau ci-dessous.

Où est le chat?

Et la première de la liste des attaques contre la stéganographie LSB est une attaque visuelle. Ça a l'air bizarre, non? Après tout, le chat avec un secret ne s'est pas trahi comme un stégoconteneur rempli à première vue. Hmmm ... Vous avez juste besoin de savoir où chercher. Il est facile de deviner que seul le NZB mérite notre attention.

Pour un stegocontainer rempli, l'image avec NZB ressemble à ceci:



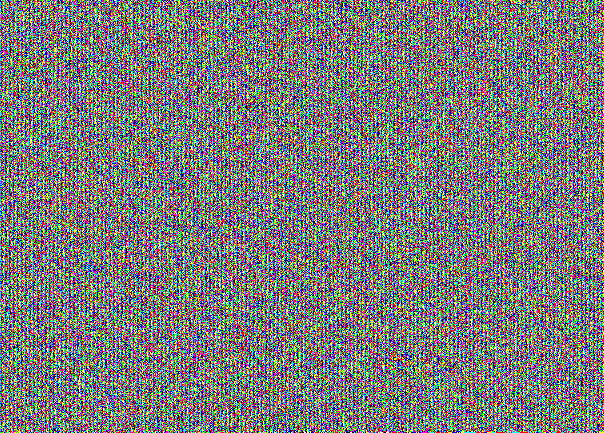
Ne croyez pas? Ici, vous avez NZB des trois canaux séparément:




Il s'agit d'un "dessin" spécifique pour masquer le message dans le NZB. À première vue, cela semble être un simple bruit. Mais quand on considère la structure est visible. Ici, vous pouvez voir que le stegocontainer est plein. Si nous prenions un message à 30% de la capacité d'un pauvre chat, nous aurions cette image:


Son NZB:



~ 70% du chat reste inchangé.

Ici, il vaut la peine de faire une petite digression et de parler des tailles. Qu'est-ce qu'un chat à 30%? La taille du chat est de 603x433 pixels. 30% de cette taille est de 78459 pixels. Chaque pixel contient 3 bits d'informations. Total 78459 3 = 235377 bits ou un peu moins de 30 kilo-octets correspond à 30% du sceau. Et dans l'ensemble, le chat s'adaptera à environ 100 kilo-octets. De telles choses.

Mais nous sommes là pour vous pour une raison. Comment donc tromper les yeux?
Première pensée: coller le message dans le bruit. Mais ce n'était pas là. Vient ensuite un fragment du stegocontainer rempli et son LSB.



Avec un petit effort, nous pouvons encore discerner une structure familière. Ne perdez pas espoir, messieurs!

Hee hee hee

Beaucoup de choses brisent les statistiques, vous savez.

En changeant quelque chose dans l'image, nous changeons ses propriétés statistiques. Il suffit à l'analyste de trouver un moyen de corriger ces changements.

Le bon vieux chi carré a été créé par Andreas Wesfield et Andreas Pfitzmann de l'Université de Dresde dans leur ouvrage «Attacks on Steganographic Systems», qui peut être trouvé ici.

Ci-après, nous parlerons d'attaques dans le même plan de couleur, ou dans le contexte du RVB, d'attaques sur un canal. Les résultats de chaque attaque peuvent être réduits à la moyenne et obtenir le résultat de l'image «assemblée».

Ainsi, l'attaque du chi carré est basée sur l'hypothèse que la probabilité d'apparition simultanée de couleurs voisines (différentes par le bit le moins significatif) (paire de valeurs) dans un stegocontainer vide est extrêmement faible. C'est vraiment, vous pouvez le croire. En d'autres termes, le nombre de pixels de deux couleurs adjacentes est significativement différent pour un conteneur vide. Tout ce que nous devons faire est de calculer le nombre de pixels de chaque couleur et d'appliquer quelques formules. En fait, il s'agit d'une tâche simple pour tester une hypothèse à l'aide du test du chi carré.

Un peu de maths?

Soit h un tableau au i-ème endroit contenant le nombre de pixels de la i-ème couleur dans l'image étudiée.

Ensuite:

1. Fréquence de couleur mesurée $$$i = 2k$ :
   

   $$

   $$n_k = h [2k], ~ k \ in [0, 127];$$
   
   
2. Fréquence de couleur théoriquement attendue $$$i = 2k$ :
   

   $$

   $$n_k ^ * = \ frac {h [2k] + h [2k + 1]} {2}, ~ k \ in [0,127];$$
   
   

Traduire cela en Python produira quelque chose comme ceci:

for k in range(0, len(histogram) // 2): expected.append(((histogram[2 * k] + histogram[2 * k + 1]) / 2)) observed.append(histogram[2 * k]) 

Où l'histogramme est le nombre de pixels de couleur i dans l'image, $$$i \ in [0, 255]$

Le critère du khi carré pour le nombre de degrés de liberté k-1 est calculé comme suit (k est le nombre de couleurs différentes, soit 256):

$$

$$\ chi_ {k-1} ^ 2 = \ sum_ {i = 1} ^ {k} \ frac {(n_k - n_k ^ *) ^ 2} {n_k ^ *};$$

Et enfin, P est la probabilité que les distributions $$$n_i$ et $$$n_i ^ *$ dans ces conditions, ils sont égaux (la probabilité que nous ayons un stégoconteneur rempli). Il est calculé en intégrant la fonction de lissage:

$$

$$P = 1 - \ frac {1} {2 ^ {\ frac {k-1} {2}} \ Gamma (\ frac {k-1} {2})} \ int_0 ^ {\ chi_ {k-1 } ^ 2} e ^ {- \ frac {x} {2}} x ^ {\ frac {k-1} {2} -1} dx;$$

Il est plus efficace d'appliquer un chi carré non pas à l'image entière, mais seulement à ses parties, par exemple, aux lignes. Si la probabilité calculée pour la ligne est supérieure à 0,5, remplissez la ligne de l'image d'origine avec du rouge. Si moins, alors vert. Pour un chat avec 30% de satiété, l'image ressemblera à ceci:



C'est vrai, non?

Eh bien, nous avons eu une attaque mathématique, vous ne pouvez pas tromper les mathématiques! Ou ... ??

Danse aléatoire

L'idée est assez simple: écrire des bits non pas dans l'ordre, mais à des endroits aléatoires. Pour ce faire, vous devez prendre le PRSP, le configurer pour émettre le même flux aléatoire avec le même côté (aka mot de passe). Sans connaître le mot de passe, nous ne pourrons pas configurer le PRNG et trouver les pixels dans lesquels le message est caché. Nous allons le tester sur un chat.

Chaton (32% d'achèvement):



Son LSB:



L'image semble bruyante, mais pas suspecte pour un analyste inexpérimenté. Que dit le chi carré?


Il semble que le chapeau noir ait gagné!? Peu importe comment ...

Régularité-Singularité

Une autre méthode statistique a été Jessica Friedrich, Miroslav Golyan et Andreas Pfitzman en 2001. Elle a été nommée méthode RS. L'article original peut être pris ici.

La méthode contient plusieurs étapes préparatoires.

L'image est divisée en groupes de n pixels. Par exemple, 4 pixels consécutifs d'affilée. En règle générale, ces groupes contiennent des pixels adjacents.
Pour notre chat à remplissage séquentiel dans le canal rouge, les cinq premiers groupes seront:

• [78, 78, 79, 78]
  
• [78, 78, 78, 78]
  
• [78, 79, 78, 79]
  
• [79, 76, 79, 76]
  
• [76, 76, 76, 77]
  

(Toutes les mesures sont dans la version classique de RGB)

Ensuite, nous définissons la fonction dite discriminante ou fonction de lissage, qui mappe chaque groupe de pixels sur un nombre réel. Le but de cette fonction est de capturer la régularité ou la «régularité» du groupe de pixels G. Plus le groupe de pixels est bruyant $$$G = (x_1, ..., x_n)$ , plus la fonction discriminante sera importante. Le plus souvent, une «variation» d'un groupe de pixels est choisie, ou, plus simplement, la somme des différences de pixels voisins dans un groupe. Mais il peut également prendre en compte des hypothèses statistiques sur l'image.

$$

$$f (x_1, x_2, ..., x_n) = \ sum_ {i = 1} ^ {n-1} | x_ {i + 1} - x_i |$$

Les valeurs de la fonction de lissage pour un groupe de pixels de notre exemple:

• f (78, 78, 79, 78) = 2
• f (78, 78, 78, 78) = 0
• f (78, 79, 78, 79) = 3
• f (79, 76, 79, 76) = 9
• f (76, 76, 76, 77) = 1

Ensuite, la classe des fonctions de retournement à partir d'un pixel est déterminée.

Ils doivent avoir des propriétés.

$$

$$1. ~~~ \ forall x \ in P: ~ F (F (x)) = x, ~~ P = \ {0, ~ 255 \};$$

$$

$$2. ~~~ F_1: 0 \ leftrightarrow 1, ~ 2 \ leftrightarrow 3, ~ ..., 254 \ leftrightarrow 255;$$

$$

O Where $$$F$ - toute fonction d'une classe, $$$F_1$ Est une fonction de retournement direct, et $$$F _ {- 1}$ - inverser. De plus, la fonction de retournement identique est généralement désignée $$$F_0$ ce qui ne change pas le pixel.

Les fonctions de retournement de python pourraient ressembler à ceci:

 def flip(val): if val & 1: return val - 1 return val + 1 def invert_flip(val): if val & 1: return val + 1 return val - 1 def null_flip(val): return val 

Pour chaque groupe de pixels, nous appliquons l'une des fonctions de retournement et en fonction de la valeur de la fonction discriminante avant et après le retournement, nous déterminons le type de groupe de pixels: normal ( R egulaire), unique / inhabituel ( S ingulaire), et inutile inutilisable. Comme ce dernier type n'est plus utilisé, la méthode a été nommée d'après les premières lettres des types de clé. C'est tout le secret du nom, la singularité n'a rien à voir avec ça :)



Nous pouvons vouloir appliquer un retournement différent à différents pixels, pour cela nous définissons un masque M avec n valeurs de -1, 0 ou 1.

$$

$$F_M (G) = (F_ {M (1)} (x_1), F_ {M (2)} (x_2), ..., F_ {M (n)} (x_n))$$

Soit le masque de notre exemple classique - [1, 0, 0, 1]. Il a été constaté expérimentalement que les masques symétriques qui ne contiennent pas $$$F _ {- 1}$ . Les options réussies seraient également: [0, 1, 0, 1], [0, 1, 1, 0], [1, 0, 1, 0]. Nous appliquons le retournement pour les groupes de l'exemple, calculons la valeur de lissage et déterminons le type de groupe de pixels:

• $$$F_m$ (78, 78, 79, 78) = [79, 78, 79, 79];
  f (79, 78, 79, 79) = 2 = 2 = f (78, 78, 79, 78)
  Groupe inutilisable
  
  
• $$$F_m$ (78, 78, 78, 78) = [79, 78, 78, 79];
  f (79, 78, 78, 79) = 2> 0 = f (78, 78, 78, 78)
  Groupe régulier
  
  
• $$$F_m$ (78, 79, 78, 79) = [79, 79, 78, 78];
  f (79, 79, 78, 78) = 1 <3 = f (78, 79, 78, 79) Groupe singulier
  
  
• $$$F_m$ (79, 76, 79, 76) = [78, 76, 79, 77];
  f (78, 76, 79, 77) = 7 <9 = f (79, 76, 79, 76) Groupe singulier
  
  
• $$$F_m$ (76, 76, 76, 77) = [77, 76, 76, 76];
  f (77, 76, 76, 76) = 1 = 1 = f (76, 76, 76, 77)
  Groupe inutilisable
  
  

On note le nombre de groupes réguliers pour le masque M comme $$$R_M$ (en pourcentages de tous les groupes), et $$$S_M$ pour les groupes singuliers.

Alors $$$R_M + S_M \ leq 1$ et $$$R _ {- M} + S _ {- M} \ leq 1$ , pour un masque négatif (tous les composants du masque sont multipliés par -1), car $$$R_M + S_M + U_M = 1$ tout $$$U_M$ peut être vide. De même pour un masque négatif.

L'hypothèse statistique principale est que dans une image typique, la valeur attendue $$$R_M$ égal à $$$R _ {- M}$ , et il en va de même pour $$$S_M$ et $$$S _ {- M}$ . Ceci est prouvé par des données expérimentales et certaines danses avec un tambourin autour de la dernière propriété de la fonction de retournement.

$$

$$R_M \ cong S_M ~~~~ R _ {- M} \ cong S _ {- M}$$

Vérifions-le sur notre petit exemple? Étant donné la petite taille de l'échantillon, nous ne pouvons pas confirmer cette hypothèse. Voyons ce qui se passe avec le masque inversé: [-1, 0, 0, -1].

• F_M (78, 78, 79, 78) = [77, 78, 79, 77];
  f (77, 78, 79, 77) = 4> 2 = f (77, 78, 79, 77)
  Groupe régulier
  
  
• F_M (78, 78, 78, 78) = [77, 78, 78, 77];
  f (77, 78, 78, 77) = 2> 0 = f (78, 78, 78, 78)
  Groupe régulier
  
  
• F_M (78, 79, 78, 79) = [77, 79, 78, 80];
  f (77, 79, 78, 80) = 5> 3 = f (78, 79, 78, 79)
  Groupe régulier
  
  
• F_M (79, 76, 79, 76) = [80, 76, 79, 75];
  f (80, 76, 79, 75) = 11> 9 = f (79, 76, 79, 76)
  Groupe régulier
  
  
• F_M (76, 76, 76, 77) = [75, 76, 76, 78];
  f (75, 76, 76, 78) = 3> 1 = f (76, 76, 76, 77)
  Groupe régulier
  
  

Eh bien, tout est évident.

Cependant, la différence entre $$$R_M$ et $$$S_M$ ont tendance à zéro lorsque la longueur m du message intégré augmente et nous obtenons que $$$R_M \ cong S_M$ .

C'est drôle que la randomisation de l'avion LSB ait l'effet inverse sur $$$R _ {- M}$ et $$$S _ {- M}$ . Leur différence augmente avec la longueur m du message intégré. Une explication de ce phénomène peut être trouvée dans l'article original.

Voici l'horaire $$$R_M$ , $$$S_M$ , $$$R _ {- M}$ et $$$S _ {- M}$ en fonction du nombre de pixels avec LSB inversés, il est appelé un diagramme RS. L'axe des x est le pourcentage de pixels avec des LSB inversés, l'axe des y est le nombre relatif de groupes réguliers et singuliers avec les masques M et -M, $$$M = [0 ~ 1 ~ 1 ~ 0]$ .



L'essence de la méthode de stéganalyse RS est d'évaluer les quatre courbes du diagramme RS et de calculer leur intersection par extrapolation. Supposons que nous ayons un stegocontainer avec un message de longueur inconnue p (en pourcentage de pixels) intégré dans les bits inférieurs des pixels sélectionnés au hasard (c'est-à-dire en utilisant RandomLSB). Nos mesures initiales du nombre de groupes R et S correspondent à des points $$$R_M (p / 2)$ , $$$S_M (p / 2)$ , $$$R _ {- M} (p / 2)$ et $$$S _ {- M} (p / 2)$ . Nous prenons des points d'exactement la moitié de la longueur du message, car le message est un flux binaire aléatoire et en moyenne, comme mentionné précédemment, seulement la moitié des pixels sera modifiée par l'incorporation du message.

Si nous inversons le LSB de tous les pixels de l'image et calculons le nombre de groupes R et S, nous obtenons quatre points $$$R_M (1-p / 2)$ , $$$S_M (1-p / 2)$ , $$$R _ {- M} (1-p / 2)$ et $$$S _ {- M} (1-p / 2)$ . Étant donné que ces deux points dépendent de la randomisation spécifique du LSB, nous devons répéter ce processus plusieurs fois et évaluer $$$R_M (1/2)$ et $$$S_M (1/2)$ à partir d'échantillons statistiques.

Nous pouvons conditionnellement tracer des lignes à travers des points $$$R _ {- M} (p / 2)$ , $$$R _ {- M} (1-p / 2)$ et $$$S _ {- M} (p / 2)$ , $$$S _ {- M} (1-p / 2)$ .

Des points $$$R_M (p / 2)$ , $$$R_M (1/2)$ , $$$R_M (1-p / 2)$ et $$$S_M (p / 2)$ , $$$S_M (1/2)$ , $$$S_M (1-p / 2)$ définir deux paraboles. Chaque parabole et la ligne correspondante se croisent à gauche. La moyenne arithmétique des coordonnées x des deux intersections nous permet d'estimer la longueur de message inconnue p.

Pour éviter une longue estimation statistique des points médians RM (1/2) et SM (1/2), quelques autres considérations peuvent être prises:

1. Point d'intersection de courbe $$$R_M$ et $$$R _ {- M}$ a la même coordonnée x que le point d'intersection pour les courbes $$$S_M$ et $$$S _ {- M}$ . Il s'agit essentiellement d'une version plus rigoureuse de notre hypothèse statistique. (voir ci-dessus)
2. Les courbes RM et SM se coupent à m = 50%, ou $$$R_M (1/2) = S_M (1/2)$ .

Ces deux hypothèses fournissent une formule simple pour la longueur du message secret p. Après avoir mis à l'échelle l'axe des x pour que p / 2 devienne 0 et 1 - p / 2 devienne 1, la coordonnée x du point d'intersection est la racine de l'équation quadratique suivante



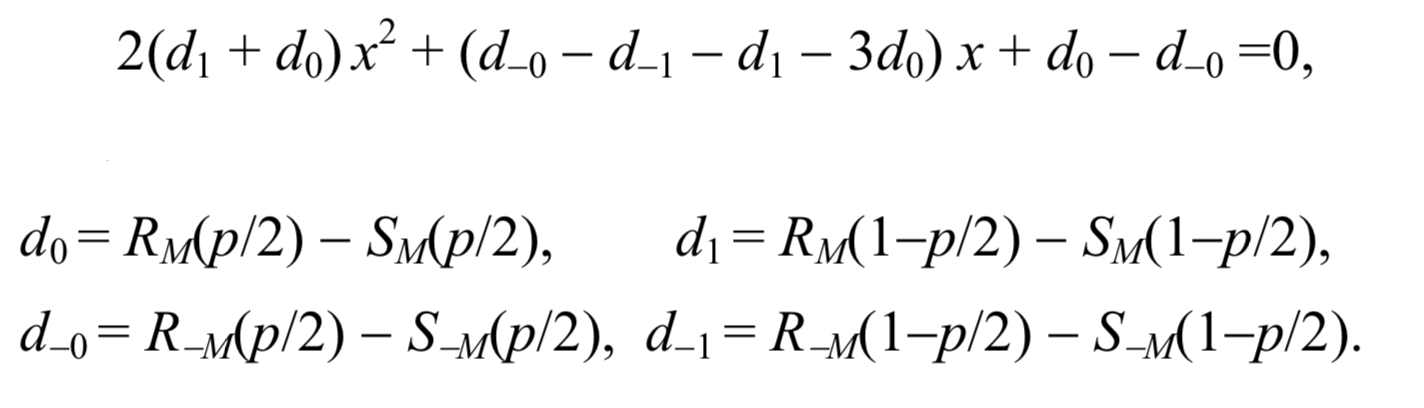
Ensuite, la longueur du message peut être calculée par la formule:

$$

$$p = \ frac {x} {x- \ frac {1} {2}}$$

Ici notre chat entre en scène. (N'est-il pas temps de lui donner un nom?)

Nous avons donc:

• Groupes RM réguliers (p / 2): 23121 pcs.
• Groupes SM singuliers (p / 2): 14124 pcs.
• Groupes réguliers avec masque inversé RM (p / 2): 37191 pcs.
• Groupes singuliers avec masque inversé SM (p / 2): 8440 pcs.
• Groupes réguliers avec LSB inversé RM (1-p / 2): 20298 pcs.
• Groupes singuliers avec LSB SM inversé (1-p / 2): 16206 pcs.
• Groupes réguliers avec LSB inversé et avec masque inversé RM (1-p / 2): 40603 pcs.
• Groupes singuliers avec LSB inversé et avec masque inversé SM (1-p / 2): 6947 pcs.

(Si vous avez beaucoup de temps libre, vous pouvez les calculer vous-même, mais pour l'instant je vous suggère de croire mes calculs)

À l'ordre du jour, nous avons laissé une mathématique nue. Rappelez-vous toujours comment résoudre des équations quadratiques?

$$

$$d_0 = 8997$$

$$

$$d _ {- 0} = 28751$$

$$

$$d_1 = 4092$$

$$

$$d _ {- 1} = 33656$$

En substituant tous les d dans la formule ci-dessus, nous obtenons une équation quadratique, que nous résolvons comme enseigné à l'école.

$$

$$

$$D = (-35988) ^ 2 - 426178 * (- 19754) = 3363616992$$

$$

$$x_1 = 1,7951 ~~~~~~~~ x_2 = -0,4204$$

Prenez une racine de module plus petite , c'est-à-dire $$$x_2$ . L'estimation approximative du message intégré au chat sera alors la suivante:

$$

$$p = \ frac {-0.4204} {- 0.4204 - 0.5} = 0.4567$$

Oui, cette méthode a un gros plus et un gros moins. L'avantage est que la méthode fonctionne avec la stéganographie LSB ordinaire et la stéganographie RandomLSB. Un chi carré ne peut pas se vanter d'une telle opportunité. La méthode a reconnu notre chat à l' aspect aléatoire avec précision et a estimé la longueur du message à 0,3256, ce qui est très, très précis.

Le moins réside dans la grande (très grande) erreur de cette méthode, qui s'accroît avec le long message avec une intégration séquentielle . Par exemple, pour un chat avec une occupation de 30%, ma mise en œuvre de la méthode donne une estimation moyenne approximative pour trois canaux de 0,4633 ou 46% de la capacité totale, avec une occupation de plus de 95% - 0,8597. Mais pour un chat vide jusqu'à 0,0054. Et c'est une tendance générale indépendante de la mise en œuvre. Les résultats les plus précis avec la méthode LSB ordinaire donnent une longueur de message intégrée de 10% + - 5%.

Plus ou moins

Pour ne pas se faire prendre, il faut être inattendu et utiliser le codage ± 1. Au lieu de changer le bit le moins significatif de l'octet de couleur, nous augmenterons ou diminuerons l'octet entier d'un. Il n'y a que deux exceptions:

• nous ne pouvons pas réduire à zéro, donc nous allons l'augmenter,
  
• nous ne pouvons pas non plus augmenter 255, nous allons donc toujours diminuer cette valeur.
  

Pour toutes les autres valeurs d'octets, nous sélectionnons complètement au hasard soit une augmentation d'un, soit une diminution. En plus de cette manipulation, le LSB changera comme avant. Pour une plus grande fiabilité, il est préférable de prendre des octets aléatoires pour enregistrer un message.

Voici notre ami chat:



Extérieurement, l'introduction est imperceptiblement exactement pour la même raison que les différences entre (0, 0, 0) et (1, 1, 1) n'étaient pas visibles.



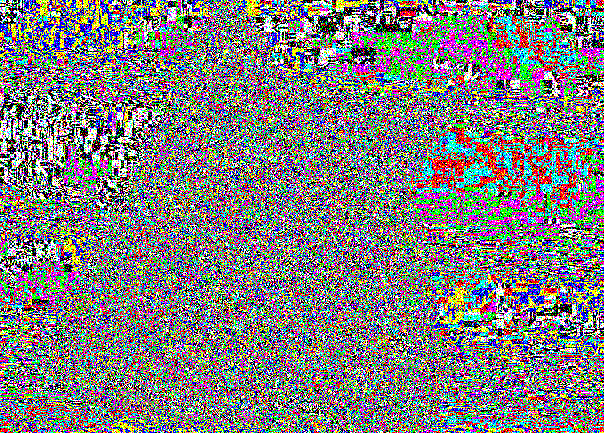
La tranche LSB reste simplement bruyante en raison de l'enregistrement dans des endroits aléatoires.



Le chi carré est toujours aveugle et la méthode RS donne une estimation approximative de 0,0036 .

Pour ne pas être très content, lisez cet article ici.

Les plus attentifs peuvent demander comment obtenir un message si des octets entiers sont modifiés de manière aléatoire, et nous n'avons pas de mot de passe pour définir le PRNG (il est préférable d'utiliser des graines différentes aka l'état du générateur aka des mots de passe pour travailler avec RandomLSB et l'encodage ± 1). La réponse est aussi simple que possible. Nous recevons le message de la même manière que nous l'avons fait sans encodage ± 1. Nous ne connaissons peut-être même pas son utilisation. Je répète, nous utilisons cette astuce uniquement pour contourner les outils de détection automatique . Lors de l'incorporation / récupération d'un message, nous travaillons uniquement avec son LSB et rien de plus. Cependant, lors de la détection, nous devons prendre en compte le contexte de mise en œuvre, c'est-à-dire tous les octets de l'image, afin de construire des estimations statistiques. C'est précisément tout le succès du codage ± 1.

Au lieu d'une conclusion

Une autre très bonne tentative d'utiliser des statistiques contre la stéganographie LSB a été faite dans une méthode appelée paires d'échantillons. Vous pouvez le trouver ici. Sa présence ici rendrait l'article trop académique, donc je le laisse intéressé pour une lecture parascolaire. Mais en anticipant les questions du public, je répondrai tout de suite: non, il ne capte pas ± 1 codage.

Et bien sûr, l'apprentissage automatique. Les méthodes modernes basées sur ML donnent de très bons résultats. Vous pouvez en lire plus ici et ici .

Sur la base de cet article, un petit outil a été écrit (pour l'instant). Il peut générer des données, effectuer une attaque visuelle séparément sur les canaux, calculer l'évaluation RS-, SPA et visualiser les résultats du chi carré. Et elle ne va pas s'arrêter là.

Pour résumer, je veux donner quelques conseils:

• Incorporez le message dans des octets aléatoires.
• Réduisez autant que possible la quantité d'informations intégrées (rappelez-vous Oncle Hamming).
• Utilisez le codage ± 1.
• Choisissez des images avec LSB bruyant.
• UPD de Remdalp : utilisez des images qui n'apparaissent nulle part.
• Soyez gentil!

Je serai heureux de voir vos suggestions, ajouts, corrections et autres commentaires!

PS Je tiens à remercier tout particulièrement PavelMSTU pour les consultations et les coups de pied de motivation.