Détection des couleurs des voitures à l'aide de réseaux de neurones et de TensorFlow

Bonjour, je m'appelle Roman Lapin, je suis étudiant en 2ème année de la faculté de l'Ecole Supérieure de Physique Générale et Appliquée de l'UNN. Cette année, j'ai réussi à passer au travers de la sélection et à participer aux travaux d'Intel Summer School à Nizhny Novgorod. Ma tâche était de déterminer la couleur de la voiture à l'aide de la bibliothèque Tensorflow, sur laquelle j'ai travaillé avec mon mentor et ingénieur de l'équipe ICV Alexei Sidnev.
Et c'est ce que j'ai.

Cette tâche comporte plusieurs aspects:

1. La voiture peut être peinte en plusieurs couleurs, comme sur KDPV. Et dans l'un des ensembles de données, par exemple, nous avions une voiture camouflée.
2. En fonction de l'éclairage et de la caméra qui prend des photos de ce qui se passe sur la route, les voitures de la même couleur seront très différentes. Les voitures «éclairées» peuvent avoir une très petite partie correspondant à la «vraie» couleur de la voiture.

Détection de couleur de voiture

La couleur de la voiture est une substance plutôt étrange. Le fabricant a une compréhension claire de la couleur de la voiture qu'ils produisent, par exemple: fantôme, glace, perle noire, pluton, chaux, krypton, angkor, cornaline, platine, bleus. La police de la circulation a une opinion sur les couleurs des voitures plutôt conservatrice et très limitée. Chaque personne a une perception subjective de la couleur (vous pouvez vous rappeler l'histoire populaire de la couleur de la robe). Ainsi, nous avons décidé de baliser comme suit.

Sur chaque image, les coordonnées des sommets des rectangles bordant les voitures ont été marquées (ci-après j'utiliserai la version anglaise - boîte de délimitation de voiture ) et à l'intérieur se trouvent les zones qui décrivent le mieux la couleur des véhicules ( boîte de couleur ). Le nombre de ces derniers est égal à la couleur de la voiture ( n x boîte de couleur - voiture n-couleur).

Ci-après, les numéros de voiture sont flous pour la possibilité de publier des photos dans le domaine public.


Jeu de données de marquage des voitures

À l'avenir, nous avons travaillé avec deux espaces colorimétriques - RVB et LAB - avec les classes 8 et 810/81, respectivement. Pour comparer les résultats de différentes approches, nous avons utilisé 8 classes en RVB pour déterminer la couleur, qui sont obtenues en divisant le cube BGR en 8 petits cubes égaux. Ils peuvent facilement être appelés noms communs: blanc, noir, rouge, vert, bleu, rose, jaune, cyan. Pour évaluer l'erreur d'une méthode, nous avons déjà utilisé l'espace colorimétrique LAB, dans lequel la distance entre les couleurs est déterminée.

Il existe deux façons intuitives de déterminer la couleur par case de couleur : couleur moyenne ou médiane. Mais dans la boîte de couleur, il y a des pixels de différentes couleurs, donc je voulais savoir avec précision comment chacune de ces deux approches fonctionne.

Pour 8 couleurs RVB pour chaque case de couleur de chaque machine du jeu de données, nous avons déterminé la couleur moyenne des pixels et la médiane, les résultats sont présentés dans les figures ci-dessous. Les «vraies» couleurs sont marquées dans les lignes - c'est-à-dire les couleurs définies respectivement comme moyenne ou comme médiane, dans les colonnes - couleurs que l'on retrouve en principe. Lors de l'ajout d'une machine à la table, le nombre de pixels de chaque couleur a été normalisé à leur nombre, c'est-à-dire que la somme de toutes les valeurs ajoutées à la ligne était égale à un.


Étude de la précision de la détermination de la couleur d'une machine comme couleur moyenne des pixels couleur 'abox. Précision moyenne: 75%


Étude de la précision de la détermination de la couleur d'une machine comme couleur médiane des pixels dans une boîte de couleur. Précision moyenne: 76%

Comme vous pouvez le voir, il n'y a pas de différence particulière entre les méthodes, ce qui indique un bon balisage. À l'avenir, nous avons utilisé la médiane, car elle a donné le meilleur résultat.
La couleur de la voiture sera déterminée en fonction de la zone à l'intérieur du cadre de délimitation de la voiture .

Avez-vous besoin de réseaux?

La question est inévitable: les réseaux de neurones sont-ils vraiment nécessaires pour résoudre une tâche intuitivement simple? Peut-être pouvez-vous prendre la couleur médiane ou moyenne des pixels dans une boîte englobante de voiture de la même manière? Les figures ci-dessous montrent le résultat de cette approche. Comme nous le montrerons plus loin, elle est pire que la méthode utilisant les réseaux de neurones.


La répartition de la part des voitures avec la valeur d'erreur L2 dans l'espace LAB entre la couleur de la zone de couleur définie comme la moyenne et la couleur de la zone de délimitation de la voiture de la valeur de cette erreur


Distribution de la part des voitures avec la valeur d'erreur L2 dans l'espace LAB entre la zone de couleur de couleur définie comme la médiane et la couleur de la zone de délimitation de la voiture à partir de la valeur de cette erreur

Description de l'approche de la tâche

Dans notre travail, nous avons utilisé l'architecture Resnet-10 pour mettre en évidence les fonctionnalités. Pour résoudre un problème à étiquette unique et à étiquettes multiples, les fonctions d'activation de softmax et sigmoid, respectivement, ont été choisies.
Un problème important était le choix de la métrique par laquelle nous pouvions comparer nos résultats. Dans le cas d'une tâche d'étiquette, vous pouvez sélectionner la classe qui correspond à la réponse maximale . Cependant, une telle solution ne fonctionnera évidemment pas dans le cas de machines multi-étiquettes / multi-couleurs, car argmax produit une couleur, très probablement. La métrique L1 dépend du nombre de classes, par conséquent, elle ne pouvait pas non plus être utilisée pour comparer tous les résultats. Par conséquent, il a été décidé de s'attarder sur la métrique de l'aire sous la courbe ROC (ROC AUC - aire sous la courbe) comme universelle et universellement reconnue.

Nous avons travaillé dans deux espaces colorimétriques. Le premier est le RVB standard, dans lequel nous avons choisi 8 classes: nous avons divisé le cube RVB en 8 sous-cubes identiques: blanc, noir, rouge, vert, bleu, rose, jaune, cyan. Une telle partition est très grossière, mais simple.


Divisez l'espace colorimétrique RVB en 8 zones

De plus, nous avons mené des études avec l'espace colorimétrique LAB, qui a utilisé la partition en 810 classes. Pourquoi tant? LAB a été introduit après que le scientifique américain David MacAdam a établi qu'il existe des zones de couleurs qui ne sont pas visibles à l'œil nu ( ellipses de MacAdam ). LAB a été construit de telle sorte que ces ellipses avaient l'apparence de cercles (dans la section de luminosité L constante).


Ellipses MacAdam et espace colorimétrique LAB ( source )

Au total, il y a 81 cercles dans la section de ces cercles.Nous avons franchi l'étape 10 par rapport au paramètre L (de 0 à 100), obtenant 810 classes. De plus, nous avons mené une expérience avec une classe L constante et, par conséquent, 81.

RGB et LAB

Les résultats suivants ont été obtenus pour le problème de la classe 8 et l'espace RVB:

Fonction d'activation	Tâche à étiquettes multiples	ROC AUC
softmax	-	0,97
sigmoïde	✓	0,88

Tableau des résultats de la reconnaissance des couleurs pour les machines dans un problème de 8 classes

Il semble que le résultat de la tâche multi-étiquettes soit déjà assez bon. Pour vérifier cette hypothèse, nous avons construit une matrice d'erreur, prenant 0,55 comme valeur seuil pour la probabilité. C'est-à-dire si cette valeur est dépassée en probabilité pour la couleur correspondante, nous supposons que la machine est peinte dans cette couleur. Malgré le fait que le seuil est choisi suffisamment bas, on peut voir des erreurs typiques dans la détermination de la couleur de la voiture et tirer des conclusions.


Tableau des résultats de la reconnaissance des couleurs pour les voitures en 8e classe

Il suffit de regarder les lignes correspondant aux couleurs vertes ou roses pour vous assurer que le modèle est loin d'être parfait. Sur la question de savoir pourquoi, avec une grande valeur métrique, un résultat aussi étrange et infructueux est obtenu, nous reviendrons et indiquerons immédiatement: lorsque l'on considère seulement 8 classes, un grand nombre de couleurs tombent dans les classes "blanc" et "noir", donc un tel résultat .

Par conséquent, nous allons passer à l'espace colorimétrique LAB et y mener des recherches.

Fonction d'activation	Tâche à étiquettes multiples	ROC AUC
softmax	-	0,915
sigmoïde	✓	0,846

Tableau des résultats de la reconnaissance des couleurs de la machine dans le problème de la classe 810

Le résultat est moindre, ce qui est logique, car le nombre de classes a augmenté de deux ordres de grandeur. Prenant le résultat sigmoïde comme point de départ, nous avons essayé d'améliorer notre modèle.

LAB: expériences avec différents poids

Avant cela, toutes les expériences ont été effectuées avec des poids unitaires dans la fonction de perte ( perte ):



Ici, GT est la vérité fondamentale, W est les poids.

Vous pouvez entrer une distance dans l' espace colorimétrique LAB. Disons que nous avons une unité en GT. Il correspond alors à un parallélépipède rectangulaire dans l'espace colorimétrique LAB. Ce parallélépipède (plus précisément, son centre) est retiré à une distance différente de tous les autres parallélépipèdes (encore une fois, leurs centres). En fonction de cette distance, vous pouvez expérimenter avec les échelles suivantes:

a) Zéro à la place d'une unité en GT, et en s'éloignant d'elle - une augmentation des poids;



b) Inversement, à la place d'une unité en GT, elle en est une; lorsqu'elle est retirée, c'est une baisse de poids;



c) Option a) plus un petit additif gaussien d'une amplitude de ½ à la place d'une unité en GT;



d) Option a) plus un petit additif gaussien d'une amplitude de 1 à la place d'une unité en GT;



e) Option b) avec un petit additif à une distance maximale de l'unité en GT.



La dernière version des échelles avec lesquelles nous avons mené des expériences est, comme nous l'avons appelé, le triple Gauss, à savoir trois distributions normales avec des centres à la place des unités dans le GT, ainsi qu'à la plus grande distance d'eux.


Trois distributions normales centrées sur les unités du GT et à la plus grande distance de celles-ci

Il faudra l'expliquer plus en détail. Vous pouvez sélectionner les deux parallélépipèdes les plus éloignés et, par conséquent, les classes, et les comparer dans l'éloignement de l'original. Pour la classe correspondant à la lointaine, l'amplitude de distribution est fixée à 0,8 et pour la seconde, elle est m fois plus petite, où m est le rapport de la distance de la source à la lointaine à la distance entre la source et la proche.

Les résultats sont présentés dans le tableau. En raison du fait que dans les échelles de l'option a), il n'y avait aucun poids - juste pour les unités en GT, le résultat sur celles-ci était encore pire que le point de départ, car le réseau ne tenait pas compte des définitions de couleurs réussies, apprenant pire. Les variantes des poids b) et e) coïncidaient pratiquement, donc le résultat sur elles coïncidait. La plus forte augmentation de points de pourcentage par rapport au résultat initial a été montrée par la variante des poids f) - triple gauss.

Fonction d'activation	Nombre de cours	Type de poids	ROC AUC
sigmoïde	810	a)	0,844
		b), e)	0,848
		c)	0,888
		d)	0,879
		f)	0,909

Résultats de la reconnaissance des couleurs des machines en problème de classe 810 avec différentes options de poids

LAB: expérimenter de nouveaux labels

Nous avons donc mené des expériences avec différents poids de perte . Ensuite, nous avons décidé d'essayer de laisser les poids comme un, et de changer les étiquettes, qui sont transférées à la fonction de perte et utilisées pour optimiser le réseau. Si avant cela les étiquettes coïncidaient avec GT, maintenant ils ont décidé de réutiliser les distributions gaussiennes avec des centres à la place des unités dans GT:

La motivation de cette décision est la suivante. Le fait est qu'avec les étiquettes ordinaires, toutes les voitures des ensembles de données se répartissent en un nombre fixe de classes, moins de 810, de sorte que le réseau apprend à déterminer la couleur des voitures de ces classes uniquement. Avec de nouvelles étiquettes, les valeurs non nulles tombent dans toutes les classes, et nous pouvons nous attendre à une augmentation de la précision de la détermination de la couleur de la voiture. Nous avons expérimenté deux sigma (écarts-types) pour les distributions gaussiennes ci-dessus: 41,9 et 20,9. Pourquoi Le premier sigma est choisi comme suit: la distance minimale entre les classes (28) est prise et le sigma est déterminé à partir de la condition que la distribution diminue deux fois dans la classe adjacente au GT'noye. Et le deuxième sigma est juste deux fois plus petit que le premier.


Répartition des voitures de jeux de données d'entraînement par classes avec différentes étiquettes en perte

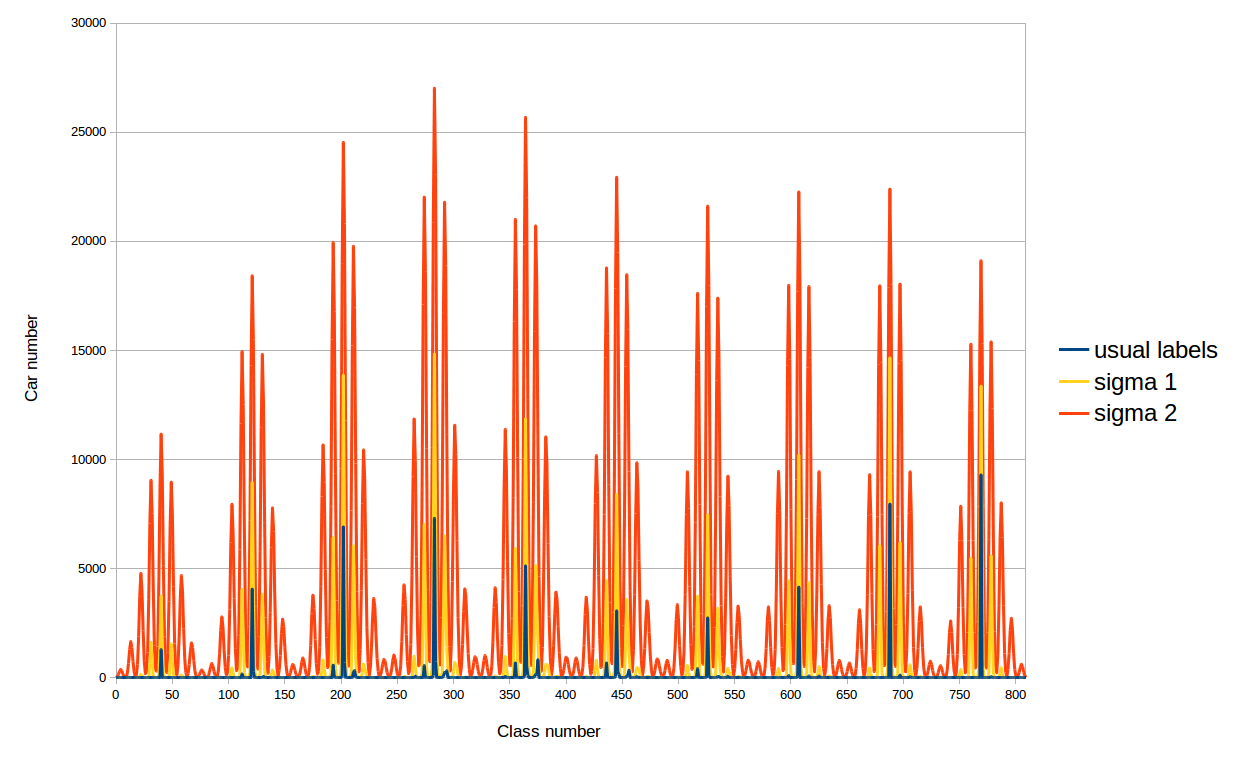
En effet, il a été possible d'améliorer encore le résultat en utilisant une telle astuce, comme le montre le tableau. En conséquence, la précision de la détermination a atteint 0,955!

Fonction d'activation	Nombre de cours	Type d'étiquette	Type de poids	ROC AUC
sigmoïde	810	habituel	ceux	0,846
		habituel	trois gauss	0,909
		nouveau, σ 1	trois gauss	0,955
		nouveau, σ 2		0,946

Résultats de la reconnaissance des couleurs pour les machines du problème de la classe 810: avec des étiquettes et des poids unitaires ordinaires, avec des étiquettes et des poids ordinaires sous forme de triple Gauss, avec de nouvelles étiquettes et des poids unitaires

LAB: 81

Si nous parlons d'expériences infructueuses, nous devons mentionner la tentative de former un réseau avec 81 classes et un paramètre constant L. Nous avons remarqué lors des expériences précédentes que la luminosité est déterminée par le réseau assez précisément, et nous avons décidé de ne former que les paramètres a et b (donc appelé les deux autres coordonnées dans LAB). Malheureusement, malgré le fait que le réseau a pu parfaitement s'entraîner dans l'avion, montrant une plus grande valeur en termes de métrique, l'idée de définir le paramètre L à la sortie du réseau comme moyenne pour la boîte de délimitation de la voiture s'est écrasé et la couleur réelle et ainsi définie était très différente.

Comparaison avec la résolution d'un problème sans utiliser de réseaux de neurones

Revenons maintenant au tout début et comparons ce qui s'est passé avec nous avec la reconnaissance de la couleur de la voiture sans utiliser de réseaux de neurones.
Les résultats sont présentés dans les figures ci-dessous. On peut voir que le pic est devenu 3 fois plus, et le nombre de voitures avec une grande erreur entre le vrai et une certaine couleur a considérablement diminué.


La répartition de la part des voitures avec la valeur d'erreur L2 dans l'espace LAB entre la zone de délimitation de la couleur de couleur définie comme la médiane et la couleur de la zone de délimitation de la voiture de la valeur de cette erreur


Distribution de la part des voitures avec la valeur d'erreur L2 dans l'espace LAB entre la couleur à la sortie du réseau de neurones et la couleur du cadre de délimitation de la voiture de la valeur de cette erreur

Des exemples

Voici des exemples de reconnaissance des couleurs de la voiture. La première est que la machine noire (un cas typique) est reconnue comme noire, et la distance dans l'espace LAB entre la vraie couleur et la couleur spécifique (18.16) est inférieure à la distance minimale entre les classes (28). Dans la deuxième figure, le réseau a pu non seulement déterminer que la voiture était éclairée (il y a une forte probabilité qui correspond à l'une des classes de couleurs blanches), mais aussi sa vraie couleur (argent). Cependant, la machine de la figure suivante, également éclairée, n'a pas été détectée par le réseau en rouge. Le réseau n'a pas pu déterminer la couleur de la voiture indiquée dans la figure ci-dessous, ce qui découle du fait que les probabilités pour toutes les couleurs sont trop faibles.

À bien des égards, la tâche était due à la nécessité de reconnaître les voitures multicolores. La dernière figure représente une voiture bicolore noire et jaune. Le réseau était le plus susceptible de reconnaître la couleur noire, qui est probablement due à la prédominance de machines de cette couleur et de couleurs similaires dans l'ensemble de données de formation, et la couleur jaune, qui est presque vraie, est entrée dans le top 3.

Courbe ROC: visualisation et problèmes

Donc, à la sortie, nous avons obtenu un résultat métrique assez élevé. La figure suivante montre les courbes ROC pour résoudre un problème avec 8 classes et pour un problème avec 810 classes, ainsi que des solutions sans utiliser de réseaux de neurones. On peut voir que le résultat est légèrement différent de celui qui a été écrit plus tôt. Les résultats précédents ont été obtenus en utilisant TensorFlow, les graphiques ci-dessous ont été obtenus en utilisant le package scikit-learn.
Courbe ROC pour plusieurs options pour résoudre le problème. À droite, le coin supérieur gauche du graphique de gauche

Vous pouvez prendre n'importe quel nombre fixe comme valeur de seuil (par exemple, Tensorflow, lorsque vous définissez le paramètre correspondant sur 50, prend le même nombre de seuils de 0 à 1 à intervalles égaux), vous pouvez utiliser les valeurs à la sortie du réseau, ou vous pouvez les limiter par le bas pour ne pas tenir compte des valeurs de l'ordre de 10 ^-4 par exemple. Le résultat de cette dernière approche est illustré dans la figure suivante.


Courbe ROC pour plusieurs options pour résoudre le problème avec un seuil de 10 ^-4

On peut voir que toutes les courbes correspondant à la solution du problème en utilisant des réseaux de neurones sont caractéristiquement meilleures (supérieures) que la solution au problème sans elles, mais vous ne pouvez pas choisir la meilleure courbe entre les premières. Selon le seuil choisi par l'utilisateur, différentes courbes correspondront à différentes solutions optimales au problème. Par conséquent, d'une part, nous avons trouvé une approche qui nous permet de déterminer avec précision la couleur de la machine et montre une métrique élevée, d'autre part, nous avons montré que la limite n'a pas encore été atteinte et que la métrique de la zone sous la courbe ROC a ses inconvénients.

Prêt à répondre aux questions et à écouter les commentaires dans les commentaires.