Une introduction simple à l'ALU pour les réseaux de neurones: explication, signification physique et mise en œuvre

Récemment, des chercheurs de Google DeepMind, dont un célèbre scientifique de l'intelligence artificielle, auteur du livre " Understanding Deep Learning ", Andrew Trask, ont publié un article impressionnant qui décrit un modèle de réseau de neurones pour extrapoler les valeurs de fonctions numériques simples et complexes avec un haut degré de précision.

Dans cet article, j'expliquerai l'architecture des NALU ( dispositifs de logique arithmétique neurale, NALU), leurs composants et les différences significatives par rapport aux réseaux de neurones traditionnels. Le principal objectif de cet article est d'expliquer simplement et intuitivement NALU (à la fois la mise en œuvre et l'idée) pour les scientifiques, les programmeurs et les étudiants qui sont nouveaux dans les réseaux de neurones et l'apprentissage en profondeur.

Note de l'auteur : Je recommande également fortement de lire l' article original pour une étude plus détaillée du sujet.

Quand les réseaux de neurones ont-ils tort?

Image tirée de cet article.

En théorie, les réseaux de neurones devraient bien se rapprocher des fonctions. Ils sont presque toujours capables d'identifier des correspondances significatives entre les données d'entrée (facteurs ou caractéristiques) et la sortie (étiquettes ou cibles). C'est pourquoi les réseaux de neurones sont utilisés dans de nombreux domaines, de la reconnaissance d'objets et leur classification à la traduction de la parole en texte et à la mise en œuvre d'algorithmes de jeu qui peuvent battre les champions du monde. De nombreux modèles différents ont déjà été créés: réseaux de neurones convolutifs et récurrents, autocodeurs, etc. La réussite de la création de nouveaux modèles de réseaux de neurones et d'apprentissage en profondeur est un grand sujet en soi.

Cependant, selon les auteurs de l'article, les réseaux de neurones ne font pas toujours face à des tâches qui semblent évidentes aux humains et même aux abeilles ! Par exemple, il s'agit d'un compte rendu oral ou d'opérations avec des chiffres, ainsi que de la capacité d'identifier la dépendance vis-à-vis des relations. L'article a montré que les modèles standard de réseaux de neurones ne peuvent même pas faire face à la cartographie identique (une fonction qui traduit un argument en lui-même, $$$f (x) = x$) Est la relation numérique la plus évidente. La figure ci-dessous montre le MSE de différents modèles de réseaux de neurones lors de l'apprentissage sur les valeurs de cette fonction.


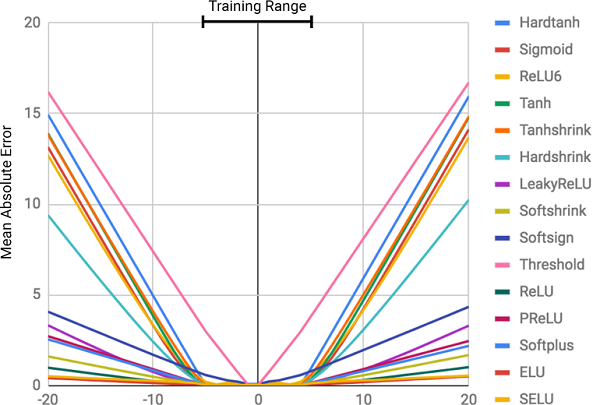La figure montre l'erreur quadratique moyenne pour les réseaux de neurones standard utilisant la même architecture et différentes fonctions d'activation (non linéaires) dans les couches internes

Pourquoi les réseaux de neurones ont-ils tort?

Comme on peut le voir sur la figure, la principale raison des échecs est la non - linéarité des fonctions d'activation sur les couches internes du réseau neuronal. Cette approche fonctionne très bien pour déterminer les relations non linéaires entre les données d'entrée et les réponses, mais il est terriblement mal d'aller au-delà des données sur lesquelles le réseau a appris. Ainsi, les réseaux de neurones se souviennent très bien d'une dépendance numérique à partir des données d'entraînement, mais ils ne peuvent pas l'extrapoler.

C'est comme entasser une réponse ou un sujet avant un examen sans comprendre le sujet. Il est facile de réussir le test si les questions sont similaires aux devoirs, mais si c'est la compréhension du sujet qui est testé, et non la capacité de se souvenir, nous échouerons.


Ce n'était pas dans le programme du cours!

Le degré d'erreur est directement lié au niveau de non-linéarité de la fonction d'activation sélectionnée. Le diagramme précédent montre clairement que les fonctions non linéaires avec des contraintes dures, comme une tangente sigmoïde ou hyperbolique ( Tanh ), peuvent faire face à la tâche de généraliser les dépendances bien pire que les fonctions à contraintes douces, telles qu'une transformation linéaire tronquée ( ELU , PReLU ).

Solution: batterie neuronale (NAC)

Une batterie neuronale ( NAC ) est au cœur du modèle NALU . Il s'agit d'une partie simple mais efficace d'un réseau de neurones qui fait face à l' addition et à la soustraction , ce qui est nécessaire pour le calcul efficace des relations linéaires.

NAC est une couche linéaire spéciale d'un réseau de neurones, sur le poids de laquelle une condition simple est imposée: ils ne peuvent prendre que 3 valeurs - 1, 0 ou -1 . Ces restrictions ne permettent pas à la batterie de modifier la plage de données d'entrée, et elle reste constante sur toutes les couches du réseau, quels que soient leur nombre et leurs connexions. Ainsi, la sortie est une combinaison linéaire des valeurs du vecteur d'entrée, qui peut facilement être une opération d'addition et de soustraction.

Réflexions à voix haute : pour une meilleure compréhension de cette déclaration, regardons un exemple de construction de couches d'un réseau neuronal qui effectuent des opérations arithmétiques linéaires sur les données d'entrée.


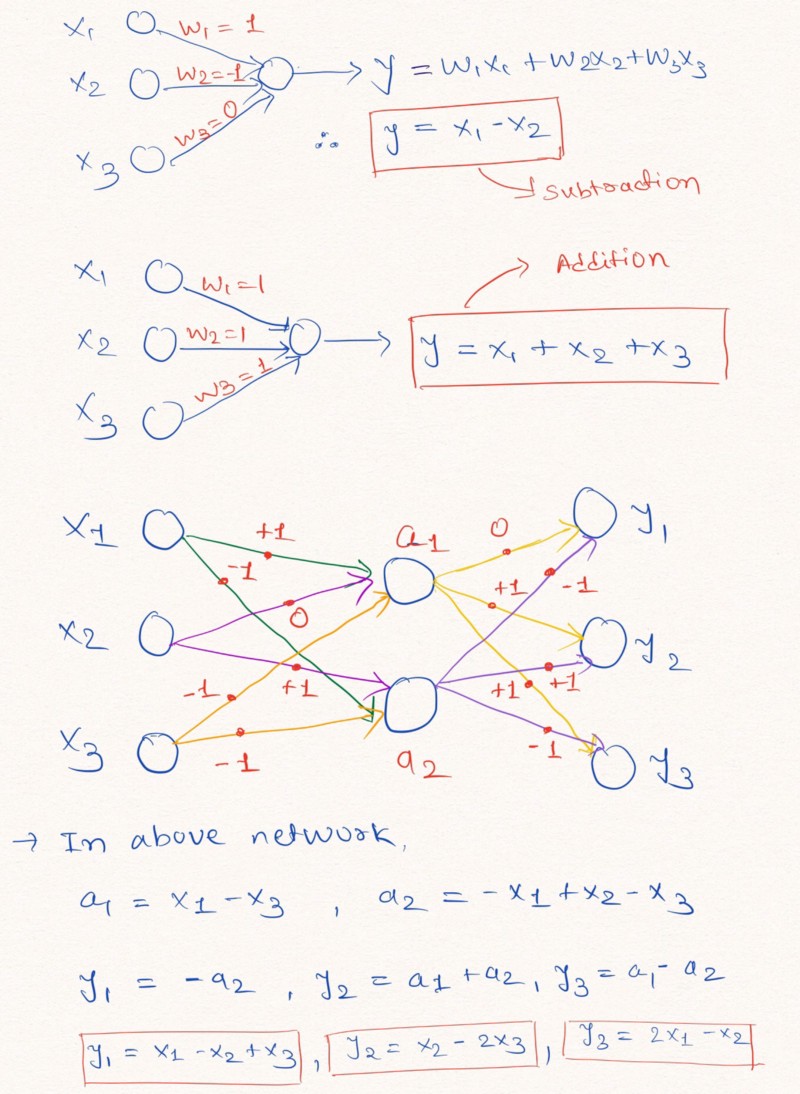La figure illustre comment les couches d'un réseau de neurones sans ajouter de constante et avec des valeurs possibles de poids -1, 0 ou 1, peuvent effectuer une extrapolation linéaire

Comme indiqué ci-dessus dans l'image des couches, le réseau neuronal peut apprendre à extrapoler les valeurs de fonctions arithmétiques simples telles que l'addition et la soustraction ( $$$y = x_1 + x_2$et $$$y = x_1 - x_2$), en utilisant les restrictions des poids avec des valeurs possibles de 1, 0 et -1.

Remarque: la couche NAC dans ce cas ne contient pas de terme libre (constant) et n'applique pas de transformations non linéaires aux données.

Étant donné que les réseaux de neurones standard ne font pas face à la solution du problème dans des restrictions similaires, les auteurs de l'article proposent une formule très utile pour calculer ces paramètres à l'aide de paramètres classiques (illimités) $$$\ chapeau {W}$et $$$\ chapeau {M}$. Les données de poids, comme tous les paramètres des réseaux de neurones, peuvent être initialisées au hasard et sélectionnées dans le processus d'apprentissage du réseau. Formule pour calculer le vecteur $$$W$à travers $$$\ chapeau {W}$et $$$\ chapeau {M}$ressemble à ceci:

$$

$$W = tanh (\ hat {W}) \ odot \ sigma (\ hat {M})$$

La formule utilise le produit matriciel élément par élément

L'utilisation de cette formule garantit la plage limitée de valeurs W par l'intervalle [-1, 1], qui est plus proche de l'ensemble -1, 0, 1. De plus, les fonctions de cette équation sont différenciables par les paramètres de poids. Ainsi, il sera plus facile pour notre couche NAC d'apprendre des valeurs $$$W$utilisant la descente de gradient et la propagation inverse de l'erreur . Ce qui suit est un schéma de l'architecture de la couche NAC .


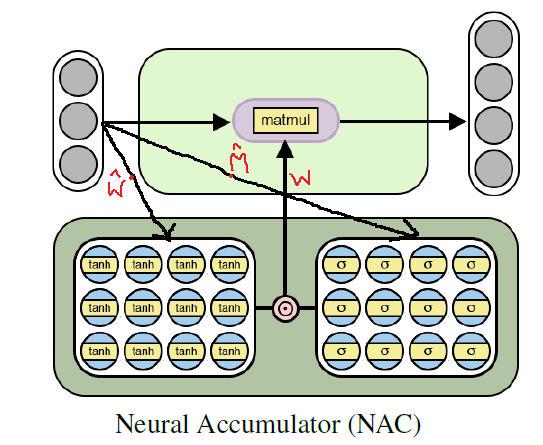L'architecture d'une batterie neuronale pour l'apprentissage des fonctions arithmétiques élémentaires (linéaires)

Implémentation de Python NAC à l'aide de Tensorflow

Comme nous l'avons déjà compris, le NAC est un réseau neuronal (couche réseau) assez simple avec de petites fonctionnalités. Ce qui suit est une implémentation d'une seule couche NAC en Python à l'aide des bibliothèques Tensoflow et NumPy.


Dans le code ci-dessus $$$\ chapeau {W}$et $$$\ chapeau {M}$sont initialisés à l'aide d'une distribution uniforme, mais vous pouvez utiliser n'importe quelle méthode recommandée pour générer une approximation initiale de ces paramètres. Vous pouvez voir la version complète du code dans mon référentiel GitHub (le lien est dupliqué à la fin du post).

En route: de l'addition et de la soustraction au NAC pour les expressions arithmétiques complexes

Bien que le modèle d'un réseau neuronal simple décrit ci-dessus fasse face à des opérations simples telles que l'addition et la soustraction, nous devons être en mesure d'apprendre des nombreuses significations de fonctions plus complexes, telles que la multiplication, la division et l'exponentiation.

Ci-dessous se trouve l'architecture NAC modifiée, qui est adaptée pour la sélection d' opérations arithmétiques plus complexes par logarithme et en prenant l'exposant à l'intérieur du modèle. Notez les différences entre cette implémentation NAC et celle déjà discutée ci-dessus.


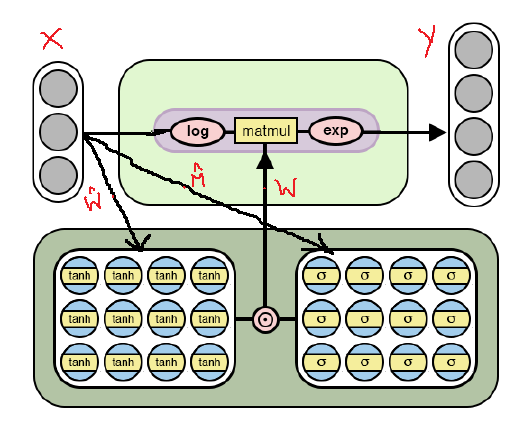Architecture NAC pour des opérations arithmétiques plus complexes

Comme on peut le voir sur la figure, nous logarithmesons les données d'entrée avant de les multiplier par la matrice de poids, puis calculons l'exposant du résultat. La formule pour les calculs est la suivante:

$$

$$Y = exp (W \ bullet (log (| x | + \ epsilon)))$$

Formule de sortie pour la deuxième version de NAC . $$$\ epsilon$voici un très petit nombre pour éviter des situations comme log (0) pendant l'entraînement

Ainsi, pour les deux modèles NAC , le principe de fonctionnement, y compris le calcul de la matrice de poids avec restrictions $$$W$à travers $$$\ chapeau {W}$et $$$\ chapeau {M}$ne change pas. La seule différence est l'utilisation d'opérations logarithmiques sur l'entrée et la sortie dans le second cas.

Deuxième version NAC en Python utilisant Tensorflow

Le code, comme l'architecture, ne changera guère, à l'exception des améliorations indiquées dans le calcul du tenseur des valeurs de sortie.



Je vous rappelle à nouveau que la version complète du code peut être trouvée dans mon référentiel GitHub (le lien est dupliqué à la fin du post).

Tout mettre ensemble: une unité de logique arithmétique neurale (NALU)

Comme beaucoup l'ont déjà deviné, nous pouvons apprendre de presque toutes les opérations arithmétiques, combinant les deux modèles discutés ci-dessus. C'est l' idée principale de NALU , qui comprend une combinaison pondérée de NAC élémentaire et complexe, contrôlée par un signal d'entraînement. Ainsi, les NAC sont les blocs de construction pour la construction des NALU , et si vous comprenez leur conception, la construction des NALU sera facile. Si vous avez encore des questions, essayez de lire à nouveau les explications des deux modèles NAC . Ci-dessous, un schéma avec l'architecture NALU .


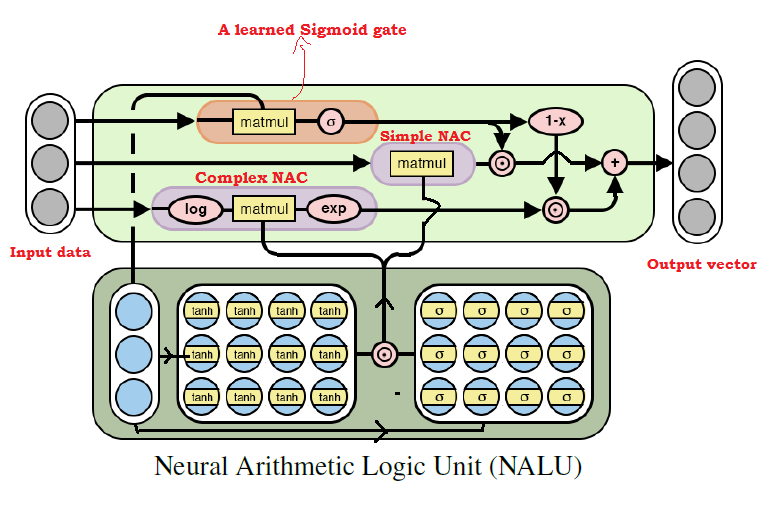Diagramme d' architecture NALU avec explications

Comme le montre la figure ci-dessus, les deux unités NAC (blocs violets) à l'intérieur de la NALU sont interpolées (combinées) via le sigmoïde du signal d'entraînement (bloc orange). Cela vous permet d'activer ou de désactiver la sortie de l'un d'entre eux, en fonction de la fonction arithmétique, dont nous essayons de trouver les valeurs.

Comme mentionné ci-dessus, l'unité élémentaire NAC est une fonction d'accumulation, qui permet à la NALU d'effectuer des opérations linéaires élémentaires (addition et soustraction), tandis que l'unité NAC complexe est responsable de la multiplication, de la division et de l'exponentiation. La sortie dans NALU peut être représentée comme une formule:


De la formule NALU ci-dessus, nous pouvons conclure qu'avec $$$g = 0$le réseau neuronal ne sélectionnera que des valeurs pour des opérations arithmétiques complexes, mais pas pour des opérations élémentaires; et vice versa - dans le cas de $$$g = 1$. Ainsi, en général, NALU est capable d'apprendre toute opération arithmétique consistant en addition, soustraction, multiplication, division et élévation à une puissance et d'extrapoler avec succès le résultat au-delà des limites des intervalles des valeurs des données source.

Implémentation de Python NALU à l'aide de Tensorflow

Dans la mise en œuvre de NALU, nous utiliserons le NAC élémentaire et complexe, que nous avons déjà défini.


Encore une fois, je note que dans le code ci-dessus, j'ai à nouveau initialisé la matrice des paramètres $$$G$en utilisant une distribution uniforme, mais vous pouvez utiliser n'importe quelle méthode recommandée pour générer une approximation initiale.

---

Résumé

Pour moi personnellement, l'idée de NALU est une percée majeure dans le domaine de l'IA, en particulier dans les réseaux de neurones, et elle semble prometteuse. Cette approche peut ouvrir la porte à ces domaines d'application où les réseaux de neurones standard ne pouvaient pas faire face.

Les auteurs de l'article parlent de diverses expériences utilisant NALU : de la sélection des valeurs des fonctions arithmétiques élémentaires au comptage du nombre de chiffres manuscrits dans une série donnée d'images MNIST , ce qui permet aux réseaux de neurones de vérifier les programmes informatiques!

Les résultats font une impression étonnante et prouvent que NALU fait face à presque toutes les tâches liées à la représentation numérique, mieux que les modèles standard de réseaux de neurones. J'encourage les lecteurs à se familiariser avec les résultats des expériences afin de mieux comprendre comment et où le modèle NALU peut être utile.

Cependant, il faut se rappeler que ni le NAC ni le NALU ne sont la solution idéale pour aucune tâche. Ils représentent plutôt l'idée générale de la façon de créer des modèles pour une classe particulière d'opérations arithmétiques.

---

Ci-dessous, un lien vers mon référentiel GitHub, qui contient l'implémentation complète du code de l'article.
github.com/faizan2786/nalu_implementation

Vous pouvez vérifier indépendamment le fonctionnement de mon modèle sur différentes fonctions en sélectionnant des hyperparamètres pour un réseau neuronal. Veuillez poser des questions et partager vos réflexions dans les commentaires sous ce post, et je ferai de mon mieux pour vous répondre.

PS (de l'auteur): c'est mon tout premier article écrit, donc si vous avez des conseils, des suggestions et des recommandations pour l'avenir (à la fois techniques et générales), veuillez m'écrire.

PPS (du traducteur): si vous avez des commentaires sur la traduction ou le texte, écrivez-moi un message personnel. Je suis particulièrement intéressé par la formulation du signal de porte appris - je ne suis pas sûr de pouvoir traduire avec précision ce terme.