Le concept de l'informatique paresseuse ne mérite guère d'être abordé en détail. L'idée de faire la même chose moins souvent, surtout si elle est longue et lourde, est aussi vieille que le monde. Parce que tout de suite au point.
Selon l'auteur de ce texte, un lénifiant normal devrait:
- Enregistrez les calculs entre les appels de programme.
- Suivez les changements dans l'arbre de calcul.
- Avoir une syntaxe modérément transparente.

Concept
Pour:
- Enregistrez les calculs entre les appels de programme:
En effet, si nous appelons le même script plusieurs dizaines de centaines de fois par jour, pourquoi devrions-nous recalculer le même chaque fois que le script est appelé, s'il est possible de stocker l'objet résultat dans un fichier. Il vaut mieux retirer un objet du disque, mais ... il faut être sûr de sa pertinence. Soudain, le script est réécrit et l'objet enregistré est obsolète. Sur cette base, nous ne pouvons pas simplement charger l'objet sur l'existence d'un fichier. Le deuxième point en découle. - Suivez les changements dans l'arbre de calcul:
La nécessité de mettre à jour l'objet doit être calculée à partir des données sur les arguments de la fonction qui le génère. Nous allons donc être sûrs que l'objet chargé est valide. En effet, pour une fonction pure, la valeur de retour ne dépend que des arguments. Cela signifie que si nous mettons en cache les résultats des fonctions pures et surveillons le changement d'arguments, nous pouvons être calmes sur la pertinence du cache. Dans le même temps, si l'objet calculé dépend d'un autre objet mis en cache (paresseux), qui à son tour en dépend un autre, vous devez déterminer correctement les modifications de ces objets, en mettant à jour en temps opportun les nœuds de chaîne qui ne sont plus pertinents. En revanche, il serait intéressant de prendre en compte que nous n'avons pas toujours besoin de charger les données de toute la chaîne de calcul. Souvent, le chargement de l'objet résultat final suffit. - Avoir une syntaxe modérément transparente:
Ce point est clair. Si, pour réécrire le script en calculs paresseux, il est nécessaire de modifier tout le code, c'est une solution moyenne. Des modifications doivent être apportées au minimum.
Ce raisonnement a conduit à une solution technique, stylisée en python par la bibliothèque evalcache (liens en fin d'article).
Solution de syntaxe et mécanisme de travail
Exemple simpleimport evalcache import hashlib import shelve lazy = evalcache.Lazy(cache = shelve.open(".cache"), algo = hashlib.sha256) @lazy def summ(a,b,c): return a + b + c @lazy def sqr(a): return a * a a = 1 b = sqr(2) c = lazy(3) lazyresult = summ(a, b, c) result = lazyresult.unlazy() print(lazyresult)
Comment ça marche?
La première chose qui attire votre attention ici est la création du décorateur paresseux. Une telle solution syntaxique est assez standard pour les pythons Python. Le décorateur paresseux reçoit un objet cache dans lequel le lénificateur stockera les résultats des calculs. Les exigences de l'interface de type dict sont superposées au type de cache. En d'autres termes, nous pouvons mettre en cache tout ce qui implémente la même interface que le type dict. Pour démontrer dans l'exemple ci-dessus, nous avons utilisé le dictionnaire de la bibliothèque Shelve.
Le décorateur reçoit également un protocole de hachage, qu'il utilisera pour construire des clés de hachage d'objets et quelques options supplémentaires (autorisation d'écriture, autorisation de lecture, sortie de débogage), qui peuvent être trouvées dans la documentation ou le code.
Le décorateur peut être appliqué aux fonctions et aux objets d'autres types. À ce moment, un objet paresseux est construit sur leur base avec une clé de hachage calculée sur la base de la représentation (ou en utilisant une fonction de hachage spécialement définie pour ce type de fonction).
Une caractéristique clé de la bibliothèque est qu'un objet paresseux peut engendrer d'autres objets paresseux, et le hachage du parent (ou des parents) sera mélangé dans la clé de hachage du descendant. Pour les objets paresseux, il est autorisé d'utiliser l'opération de prise d'un attribut, l'utilisation d'appels ( __call__ ) d'objets et l'utilisation d'opérateurs.
En passant par un script, en fait, aucun calcul n'est effectué. Pour b, le carré n'est pas calculé et pour lazyresult, la somme des arguments n'est pas prise en compte. Au lieu de cela, un arbre d'opérations est construit et les clés de hachage des objets paresseux sont calculées.
Les calculs réels (si le résultat n'a pas été précédemment mis dans le cache) seront effectués uniquement dans la ligne: result = lazyresult.unlazy()
Si l'objet a été calculé précédemment, il sera chargé à partir du fichier.
Vous pouvez visualiser l'arborescence de construction:
Construire une visualisation d'arbre evalcache.print_tree(lazyresult) ... generic: <function summ at 0x7f1cfc0d5048> args: 1 generic: <function sqr at 0x7f1cf9af29d8> args: 2 ------- 3 -------
Comme les hachages d'objets sont construits sur la base de données sur les arguments qui génèrent ces objets, lorsque l'argument change, le hachage de l'objet change et avec lui les hachages de la chaîne entière en fonction. Cela vous permet de garder les données du cache à jour en effectuant des mises à jour à temps.
Des objets paresseux s'alignent dans un arbre. Si nous effectuons une opération non perturbée sur l'un des objets, exactement autant d'objets seront chargés et comptés que nécessaire pour obtenir un résultat valide. Idéalement, l'objet nécessaire se chargera simplement. Dans ce cas, l'algorithme ne tirera pas les objets en formation dans la mémoire.
En action
Ci-dessus était un exemple simple qui montre la syntaxe mais ne démontre pas la puissance de calcul de l'approche.
Voici un exemple un peu plus proche de la vie réelle (en utilisant sympy).
Exemple utilisant sympy et numpy Les opérations de simplification des expressions symboliques sont extrêmement coûteuses et demandent littéralement une lénification. La construction d'un grand tableau prend encore plus de temps, mais grâce à la lénification, les résultats seront extraits du cache. Veuillez noter que si certains coefficients sont modifiés en haut du script où l'expression sympy est générée, les résultats seront recalculés car la clé de hachage de l'objet paresseux changera (grâce aux __repr__ ).
Très souvent, une situation se produit lorsqu'un chercheur effectue des expériences de calcul sur un objet généré depuis longtemps. Il peut utiliser plusieurs scripts pour séparer la génération et l'utilisation de l'objet, ce qui peut entraîner des problèmes de mise à jour intempestive des données. L'approche proposée peut faciliter ce cas.
De quoi s'agit-il?
evalcache fait partie du projet zencad. Il s'agit d'un petit script cadique, inspiré et exploitant les mêmes idées que openscad. Contrairement à openscad orienté maillage, zencad s'exécutant sur le noyau opencascade utilise une représentation brep des objets et les scripts sont écrits en python.
Les opérations géométriques sont souvent effectuées pendant longtemps. L'inconvénient des systèmes de script CAO est que chaque fois que vous exécutez le script, le produit est à nouveau entièrement recompté. De plus, avec la croissance et la complication du modèle, les frais généraux ne croissent pas de façon linéaire. Cela conduit au fait que vous ne pouvez travailler confortablement qu'avec des modèles extrêmement petits.
La tâche d'evalcache était de résoudre ce problème. Dans zencad, toutes les opérations sont déclarées paresseuses.
Exemples:
Exemple de construction de modèle
Ce script génère le modèle suivant:
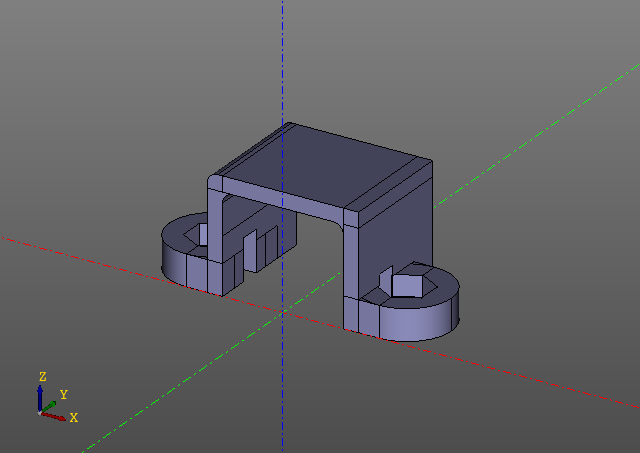
Notez qu'il n'y a pas d'appels evalcache dans le script. L'astuce est que la lénification est intégrée dans la bibliothèque zencad elle-même et n'est même pas visible à première vue, bien que tout le travail ici fonctionne avec des objets paresseux, et le calcul direct se fait uniquement dans la fonction `` affichage ''. Bien sûr, si certains paramètres du modèle sont modifiés, le modèle sera recompté à l'endroit où la première clé de hachage a été modifiée.
Modèles informatiques volumineuxVoici un autre exemple. Cette fois, nous nous limiterons aux images:
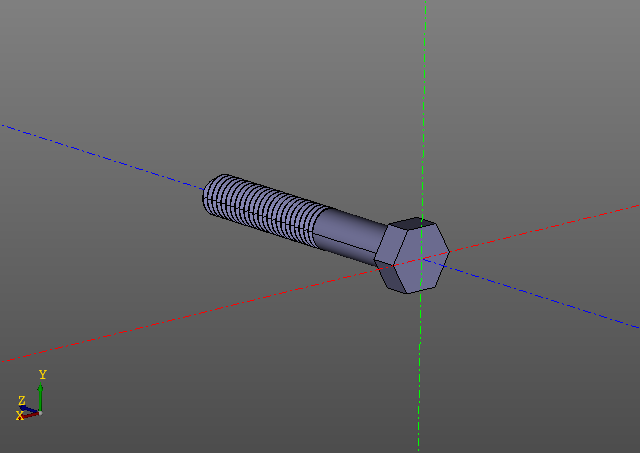
Le calcul d'une surface filetée n'est pas une tâche facile. Sur mon ordinateur, un tel boulon est construit en dix secondes environ ... L'édition d'un modèle avec des threads est beaucoup plus agréable grâce à la mise en cache.
Et maintenant, c'est un miracle:

Le croisement de surfaces filetées est une tâche de calcul complexe. Valeur pratique, cependant, rien d'autre que la vérification des mathématiques. Le calcul prend une minute et demie. Un objectif louable pour la lénification.
Les problèmes
Le cache peut ne pas fonctionner comme prévu.
Les erreurs de cache peuvent être divisées en faux positifs et faux négatifs .
Fausses erreurs négatives
Les fausses erreurs négatives sont des situations où le résultat du calcul est dans le cache, mais le système ne l'a pas trouvé.
Cela se produit si l'algorithme de clé de hachage utilisé par evalcache pour une raison quelconque a produit une clé différente pour le recalcul. Si la fonction de hachage n'est pas remplacée pour l'objet du type mis en cache, evalcache utilise le __repr__ objet pour construire la clé.
Une erreur se produit, par exemple, si la classe louée ne remplace pas l' object.__repr__ standard object.__repr__ , qui change de début en début. Ou, si le __repr__ substitué, dépend en quelque sorte d'insignifiant pour le calcul des données changeantes (comme l'adresse de l'objet ou l'horodatage).
Mauvais:
class A: def __init__(self): self.i = 3 A_lazy = lazy(A) A_lazy().unlazy()
Bon:
class A: def __init__(self): self.i = 3 def __repr__(self): return "A({})".format(self.i) A_lazy = lazy(A) A_lazy().unlazy()
Les fausses erreurs négatives conduisent au fait que la lénification ne fonctionne pas. L'objet sera recompté à chaque nouvelle exécution de script.
Fausses erreurs positives
Il s'agit d'un type d'erreur plus ignoble, car il conduit à des erreurs dans l'objet final du calcul:
Cela peut arriver pour deux raisons.
- Incroyable:
Une collision de clés de hachage s'est produite dans le cache. Pour l'algorithme sha256 ayant un espace de 115792089237316195423570985008687907853269984665640564039457584007913129639936 clés possibles, la probabilité d'une collision est négligeable. - Probable:
Une représentation d'un objet (ou d'une fonction de hachage remplacée) ne le décrit pas complètement, ou coïncide avec une représentation d'un objet d'un autre type.
class A: def __init__(self): self.i = 3 def __repr__(self): return "({})".format(self.i) class B: def __init__(self): self.i = 3 def __repr__(self): return "({})".format(self.i) A_lazy = lazy(A) B_lazy = lazy(B) a = A_lazy().unlazy() b = B_lazy().unlazy()
Les deux problèmes sont liés à un objet __repr__ incompatible. Si, pour une raison quelconque, il est impossible d'écraser le type d'objet __repr__ , la bibliothèque vous permet de définir une fonction de hachage spéciale pour le type d'utilisateur.
À propos des analogues
Il existe de nombreuses bibliothèques de lénification qui, fondamentalement, considèrent qu'il suffit d'exécuter un calcul pas plus d'une fois par appel de script.
Il existe de nombreuses bibliothèques de mise en cache de disque qui, à votre demande, enregistreront un objet avec la clé nécessaire pour vous.
Mais je ne pouvais toujours pas trouver de bibliothèques qui permettraient la mise en cache des résultats sur l'arbre d'exécution. S'il y en a, s'il vous plaît, dangereux.
Références:
Projet Github
Projet Pypi