Les systèmes de navigation inertielle (RNA) de haute précision constituent l'un des éléments les plus avancés des industries aérospatiales et militaires modernes. La tâche de ces systèmes, basés sur des accéléromètres et des gyroscopes optiques, est de déterminer les vitesses angulaires, les accélérations d'un objet en mouvement et l'orientation globale de l'objet dans un espace tridimensionnel.

Les spécificités de la modélisation RNA sont que dans le domaine de la modélisation, des mouvements rectilignes et rotationnels se produisent souvent, ce qui affecte fortement le fonctionnement de ces systèmes et, par conséquent, nécessite une prise en compte. Dans notre article, nous parlerons brièvement de l'effet Sagnac et de la manière dont les appareils basés sur celui-ci peuvent être étudiés numériquement dans le package COMSOL Multiphysics ^® .

Pour une navigation pratique, nous donnons au début un bref aperçu de l'article:

1. Que sont les gyroscopes optiques
2. Les spécificités de la prise en compte de la rotation dans la simulation
3. Effet Sagnac: base théorique
4. Modèle d'interféromètre Sagnac dans COMSOL Multiphysics ^®
5. Conclusion

Gyroscopes optiques et effet Sagnac

C'est peut-être l'interféromètre Sagnac classique qui démontre le mieux la nécessité d'un enregistrement de haute précision du mouvement non inertiel du domaine de simulation.

L'interféromètre Sagnac le plus simple comprend les composants suivants:

• Source lumineuse
• Un séparateur de faisceau qui dirige la lumière d'une source le long de deux chemins différents, puis les combine
• Un ensemble de miroirs (comprenant généralement deux ou trois miroirs)

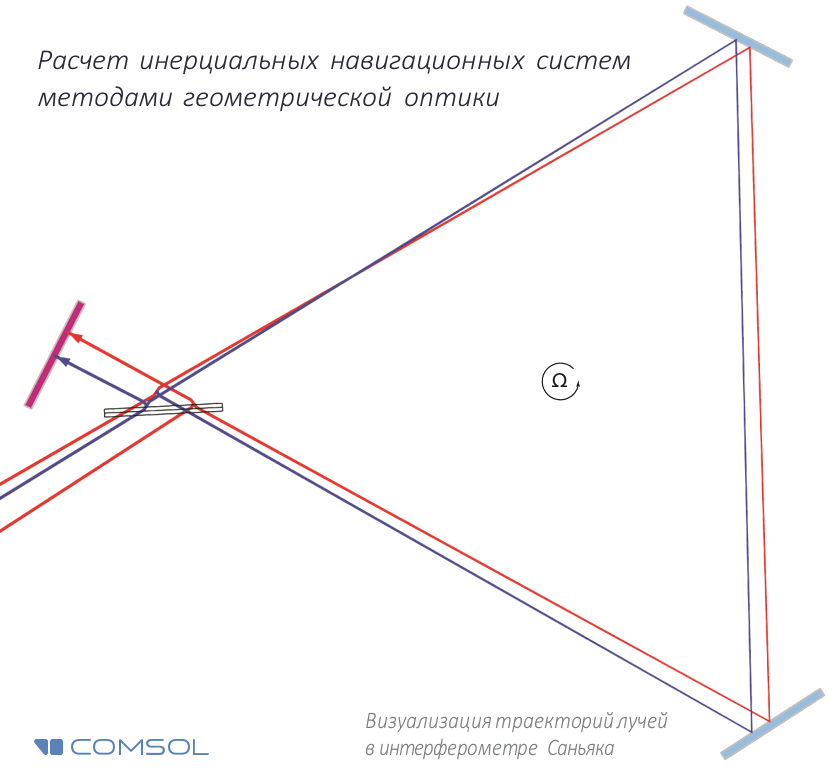
Le séparateur de faisceau et les miroirs forment une trajectoire triangulaire ou rectangulaire le long de laquelle la lumière se propage dans les deux directions. À ce moment, le système de navigation lui-même (ainsi que l'aéronef ou le vaisseau spatial dans lequel il est installé) tourne également à une certaine vitesse angulaire. En observant l'interférence des rayons lumineux (dus à l'effet Sagnac) qui se propagent le long de ces trajectoires, il est possible de déterminer la vitesse angulaire du système avec une très grande précision.

La mesure des petites rotations est essentielle pour déterminer et contrôler l'orientation des objets dans les industries de défense et spatiales modernes. Actuellement, les gyroscopes à laser annulaire et à fibre optique, dont le principe est également basé sur l'effet Sagnac, sont les plus utilisés. Notez qu'un gyroscope laser en anneau est très précis, bon marché et facile à entretenir, car, contrairement aux gyroscopes mécaniques, il ne contient pas de pièces rotatives.

Modélisation de la propagation de la lumière dans les composants optiques tournants

Comment calculer le chemin de propagation de la lumière dans un système rotatif de miroirs, prismes et diviseurs de faisceau? Afin de ne pas plonger dans la théorie de la relativité, supposons que la vitesse de rotation est bien inférieure à la vitesse de la lumière, mais elle est suffisamment grande pour que nous devions prendre en compte la rotation. Il existe au moins deux approches pour résoudre ce problème:

1. Réécrire les équations de propagation de la lumière dans un référentiel non inertiel
2. Faites pivoter la structure en temps réel lors de la propagation des rayons

La différence entre ces approches est que dans un cas le modèle est dans un référentiel non inertiel relié à un interféromètre mobile (option n ° 1), ou dans un référentiel «laboratoire» fixé dans l'espace (option n ° 2). La seconde option étant beaucoup plus simple à mettre en œuvre, nous utiliserons cette approche pour simuler l'interféromètre de Sagnac.

Le package COMSOL Multiphysics ^® est assez efficace pour modéliser des appareils à structure mobile ou déformante (qui incluent l'interféromètre Sagnac et un gyroscope laser en anneau) et vous permet d'intégrer et de simuler divers processus physiques interdisciplinaires au sein d'un même modèle de calcul.

L'analyse des structures déformables et mobiles est traditionnellement réalisée avec un soin particulier, car elle est utilisée dans divers domaines: dans l'analyse des contraintes thermiques, l'interaction d'un fluide avec une structure, les écoulements polyphasiques, ainsi qu'en galvanoplastie, les dispositifs piézoélectriques, etc. En fait, pour un tracé précis des rayons dans une structure en mouvement, il suffira d'indiquer la vitesse angulaire du système, puis de lancer un calcul standard basé sur les technologies d'optique géométrique .

Effet Sagnac: base théorique

Avant de passer à la description du modèle implémenté dans le package, examinons brièvement ce qu'est l'effet Sagnac.

Imaginez que la lumière se déplace strictement autour d'un cercle (par exemple, le long d'un câble à fibre optique) dans deux directions opposées, comme illustré sur la Fig. 1. Point de déclenchement du faisceau - $$$P_0$. La ligne pointillée indique le sens horaire et la ligne continue épaisse indique le sens antihoraire. Les rayons lumineux dans ce cadre seront opposés les uns aux autres, car ils se propagent autour de la circonférence dans des directions opposées.

Si l'anneau était immobile, les trajectoires des rayons se croiseraient deux fois: d'abord au point opposé du cercle, puis au point de départ $$$P_0$. Imaginez maintenant que l'anneau tourne dans le sens antihoraire autour de son centre avec une certaine vitesse angulaire. Si on suit le mouvement du point $$$P_0$lors de la propagation de la lumière, nous verrons qu'un rayon se propageant dans le sens des aiguilles d'une montre lui reviendra lorsqu'il est déjà dans une nouvelle position, $$$P_1$. Quand au point $$$P_0$un rayon se propageant dans le sens antihoraire reviendra, il se déplacera plus loin et sera en position $$$P_2$. $$$P_2$situé à une plus grande distance de $$$P_0$que $$$P_1$parce que le cercle tourne également dans le sens antihoraire.

Fig.1. Propagation de la lumière dans le sens horaire et antihoraire le long du bord d'un cercle tournant.

De toute évidence, l'illustration de la figure 1 est considérablement mise à l'échelle pour plus de clarté, et en réalité, la distance entre les points est 10 milliards de fois plus petite. Cependant, même dans ce cas, la différence de chemin optique parcouru entraîne un déphasage et, par conséquent, des interférences.

Sans approfondir les calculs théoriques (mais s'ils sont intéressants, nous recommandons le travail classique suivant de Post, Evert J. «Sagnac effect», Reviews of Modern Physics, 39, no. 2, p. 475, 1967 ), la relation finale entre la vitesse angulaire $$$\ Omega$et la différence de chemin optique $$$\ Delta L$peut s'exprimer comme suit:

$$

$$\ Delta L = {{4 \ Omega A} \ over {c_0}}$$

O Where $$$A$L'aire du cercle est-elle considérée, et $$$c_0$C'est la vitesse de la lumière.

En général, l'effet Sagnac est encore plus général que l'exemple décrit ci-dessus. Le chemin de propagation de deux rayons venant en sens inverse peut être de n'importe quelle forme, mais le retard entre eux sera toujours proportionnel à la taille de la région, qui est limitée par le contour dans lequel les rayons se propagent. De plus, cet effet est également observé dans les cas où le centre de rotation ne coïncide pas avec le centre du contour.

Modèle d'essai d'interféromètre de Sagnac basé sur le traçage optique des rayons

Pour vérifier comment COMSOL Multiphysics ^® sera calculé $$$\ Delta L$et, par conséquent, la sensibilité de l'appareil, nous considérons la conception de test de l'interféromètre Sagnac dans lequel la lumière ne se propage pas autour de la circonférence, mais le long du périmètre du triangle, au sommet duquel il y a deux miroirs et un séparateur de faisceau (Fig.2).

Fig.2. Schéma de l'interféromètre de Sagnac.

Le faisceau initial passe à travers un séparateur de faisceau, à la suite duquel deux rayons de même intensité sont formés. Au moment de la sortie du séparateur de faisceau, ils sont au même point et ont la même phase. Étant donné que le système de miroirs tourne, au moment où les rayons reviennent au séparateur de faisceau, leurs chemins optiques (et, par conséquent, leurs phases) sont différents les uns des autres.

En pratique, au lieu de petites quantités $$$\ Delta L$les systèmes détectent souvent un décalage de fréquence (ou fréquence de battement) $$$\ Delta \ nu$:

$$

$${{\ \ Delta \ nu} \ over {\ nu}} = {{\ Delta L} \ over {L}}$$

Ici $$$L$Est la longueur effective du contour le long duquel les rayons se propagent, et $$$\ nu$- leur fréquence. Veuillez noter que $$$\ Delta L$déterminé directement dans le calcul.

Le processus de traçage numérique des rayons peut être facilement automatisé, par exemple pour effectuer une analyse paramétrique. Dans la fig. La figure 3 montre les résultats de l'analyse paramétrique dans une large gamme de valeurs de vitesse angulaire, de relativement petite à très grande.

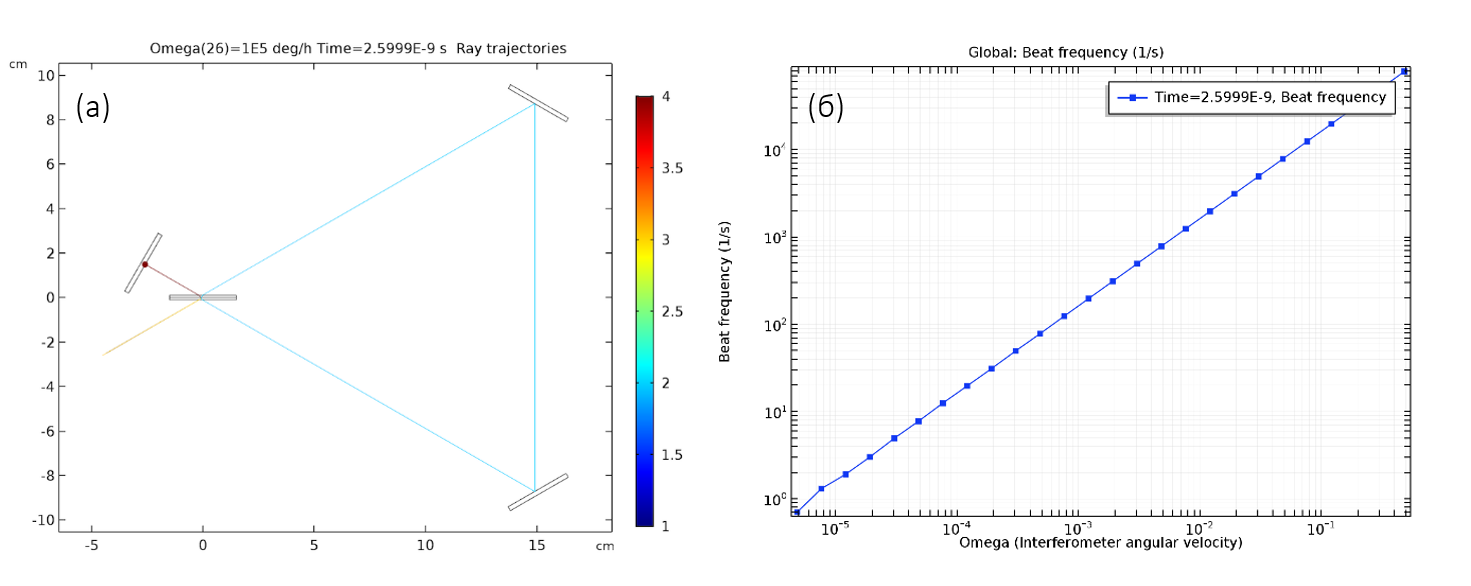
Fig.3. a) Trajectoires des rayons dans un interféromètre d'essai. Les écarts dans la trajectoire des deux rayons sont si insignifiants qu'ils ne sont pas visibles même en gros plan (b) La dépendance de la fréquence de battement sur la fréquence angulaire de rotation du système.

La fréquence de battement correspondante est en excellent accord avec les valeurs théoriques. En modifiant la distance entre les miroirs, on peut montrer que la pente de cette ligne est proportionnelle à l'aire de la région triangulaire comprise entre les rayons venant en sens inverse.

Un regard vers l'avenir ou l'application pratique de la modélisation numérique des gyroscopes optiques

Les résultats ci-dessus démontrent qu'en traçant des rayons dans une géométrie rotative (cadre) en utilisant la technique décrite, il est possible de calculer avec une grande précision la sensibilité des appareils basée sur l'effet Sagnac, si la vitesse de rotation est faible par rapport à la vitesse de la lumière (c'est-à-dire sans effets relativistes). Ainsi, grâce à ce nouveau modèle , les spécialistes de la modélisation et les ingénieurs travaillant avec des systèmes d'orientation angulaire disposeront désormais d'un gabarit de travail prêt à l'emploi pour étudier l'effet Sagnac, qui sous-tend le fonctionnement des gyroscopes à laser annulaire.

Un lecteur attentif s'interrogera probablement sur la nécessité d'une telle simulation numérique, étant donné que l'effet Sagnac est décrit avec précision par la formule ci-dessus. Il convient de noter que les vrais ANN sont beaucoup plus compliqués que la configuration la plus simple avec un séparateur de faisceau et deux miroirs, discuté ci-dessus. Ces systèmes sont installés avec d'autres appareils sensibles dans un espace limité, un cadre supplémentaire est nécessaire, ce qui garantit l'immobilité des composants optiques les uns par rapport aux autres. De plus, les RNA fonctionnent souvent dans des environnements agressifs et sont affectés par les contraintes mécaniques, la température et les champs électromagnétiques. Ces facteurs affectent le comportement et la sensibilité du gyroscope, ce qui nécessite un examen plus détaillé et approfondi, et ne peut être décrit par la même formule simple.

Ainsi, le tracé de rayons présenté dans un interféromètre Sagnac ou un gyroscope laser en anneau ne sera que la première étape d'une analyse multiphysique complexe et de haute précision de grands systèmes optiques. COMSOL Multiphysics ^® permet le traçage des rayons dans les conditions les plus réalistes, en tenant compte notamment de l'échauffement et des déformations thermiques des composants optiques, ce qui ouvrira de nouvelles possibilités pour une meilleure compréhension et évaluation de la sensibilité et de la précision des systèmes de navigation inertielle complexes.

Information additionnelle

Ce matériel est basé sur les articles suivants:

• C. Boucher. Comprendre l'effet Sagnac grâce à la simulation de l'optique des rayons , Laser Focus World, août 2018
• Simulation d'un interféromètre Sagnac et d'un gyroscope laser en anneau à l'aide de méthodes d'optique géométrique , blog d'entreprise COMSOL

Pour une connaissance plus détaillée des méthodes et exemples décrits, vous pouvez demander une version de démonstration gratuite et entièrement fonctionnelle de COMSOL Multiphysics ^® dans les commentaires ou via le lien .

Nous invitons également tout le monde le 1er novembre à l'événement principal pour les utilisateurs actuels et futurs de COMSOL - COMSOL Day à Moscou .