Passé un compromis - vous pouvez vous marier!

Présentation

La méthode des éléments finis (FEM ou FEM, ils l'ont à l'étranger) est fermement entrée dans la pratique des calculs d'ingénierie dans la conception de systèmes complexes. Dans une large mesure, cela concerne les calculs de résistance mécanique. L'application de cette méthode, mise en œuvre par le logiciel approprié, raccourcit considérablement le cycle de développement du dispositif final, éliminant la masse des contrôles expérimentaux nécessaires lors de l'utilisation de calculs classiques basés sur les méthodes de sopromat et de mécanique des structures. À ce jour, de nombreux logiciels d'application ont été développés qui implémentent FEM. À l'avant-garde se trouve le puissant ANSYS, sur les côtés et à une distance honorifique - des systèmes de CAO avec un module FEM intégré (SolidWorks, Siemens NX, Creo Parametric, Compass 3D).

CalculiX est fort, mais difficile et incompréhensible. Allons-nous résoudre ce problème?



Naturellement, la FEM a pénétré le domaine de l'éducation - pour l'utiliser dans des tâches réelles, la formation de spécialistes appropriés est nécessaire. Dans les capitales, dans les grandes universités techniques, la situation dans ce domaine est plus ou moins normale, et dans notre région, le même ANSYS est utilisé, par exemple, au Département de théorie de l'élasticité de l'Université fédérale du Sud. Mais à la périphérie, dans des universités étroitement spécialisées et peu riches, la situation est déplorable. Et c'est simple: ANSYS coûte environ 2 millions de roubles pour un lieu de travail et plus d'un endroit est nécessaire. Malheureusement, toutes les universités ne peuvent pas se permettre de payer 30 à 40 millions pour organiser un cours d'informatique pour enseigner l'utilisation du FEM.

L'une des alternatives est l'utilisation de logiciels libres dans le processus éducatif. Heureusement, de tels logiciels sont disponibles. Cependant, il n'y a pratiquement aucun matériel en russe sur son utilisation. Pour corriger cette situation, je vais consacrer cet article à l'introduction de CalculiX - un logiciel ouvert et gratuit conçu pour résoudre les problèmes tridimensionnels linéaires et non linéaires de la mécanique d'un corps solide déformable et de la mécanique des fluides et des gaz en utilisant la méthode des éléments finis.

1. Qu'est-ce que CalculiX et où l'obtenir. Installation de Windows

Le package CalculiX est un ensemble d'utilitaires de console, y compris un préprocesseur pour préparer les données source, un solveur FEM et un post-processeur pour traiter les résultats. CalculiX est utilisé à la fois indépendamment et dans le cadre d'autres produits, parmi lesquels FreeCAD gagne du terrain. Une autre question est que CalculiX est encore peu connu dans notre pays, ce qui est directement indiqué par le seul article à ce sujet sur cette ressource .

Je mentionnerai spécifiquement le matériel suivant en ce qui concerne le travail sous Windows, comme le plus courant et utilisé, y compris les établissements d'enseignement. De plus, l'utilisation de nombreux programmes gratuits est une douleur ouverte.

Si vous prenez le package Windows sur le site Web officiel de CalculiX, il devient complètement difficile de savoir quoi faire ensuite. Conjointement avec la documentation en anglais, il met fin à ce produit pour beaucoup, puis se traduit par des commentaires vénéneux sur l'impossibilité de son utilisation. Et cela est en partie vrai - le seuil d'entrée est vraiment élevé. Mais nous allons quand même essayer.

Il existe un certain nombre de versions non officielles conviviales relativement novices de ce miracle pour Windows, parmi lesquelles bConverged CalculiX pour Windows . Nous téléchargeons le kit de distribution à partir d'ici , le déballons et l'installons en utilisant la méthode standard "de plus en plus ...". L'installation ne constitue donc pas un mystère particulier et est tout à fait accessible à un utilisateur inexpérimenté. En tant qu'environnement de travail principal, ce package utilise l'éditeur de texte SciTE, qui intègre les appels aux composants CalculiX, ainsi que la possibilité de saisie interactive de commandes et il ressemble à ceci (cliquable).

2. Le problème de la flexion du faisceau et sa solution analytique à l'aide des méthodes sopromat

Prenons un problème simple de l'élève - la flexion d'une poutre en acier, dont une extrémité est pincée, et la force verticale F est appliquée à l'autre.



Les paramètres du problème sont les suivants: F = 10 kN; l = 1 m est la longueur du faisceau; h = 0,1 m et b = 0,05 m sont les dimensions de la section transversale. Par souci de simplicité, nous ne prendrons pas en compte le poids propre de la poutre, car elle, avec un poids de poutre de 39 kg, est nettement inférieure à la charge appliquée. Nous trouvons la contrainte normale maximale dans la section de poutre et calculons également la déviation du faisceau due à la déformation en flexion.

Tout étudiant qui n'a pas sauté un compromis résoudra facilement un tel problème. Afin de ne pas gêner les nobles dons, je vais envelopper tous les détails de la décision dans un spoiler


Pour ceux qui sont trop paresseux pour regarder sous le spoiler, je donnerai immédiatement la réponse au problème: la tension normale maximale dans la section du faisceau $$$\ sigma_x = 119$MPa, et la flèche maximale est de 3,97 mm. Ces chiffres sont donnés pour une comparaison ultérieure avec ce que la procédure pour résoudre ce problème dans CalculiX nous donnera.

3. Préparation de la géométrie et de la grille de calcul

Tout d'abord, vous devez entrer des données géométriques sur la pièce en question dans CalculiX. Oui, il est possible d'exporter la géométrie à partir de CADs, comme cela se fait dans le même ANSYS, mais nous allons passer par la torture et entrer la géométrie manuellement. Ouvrez l'éditeur SciTE à partir du kit bConverged et saisissez le texte suivant

pnt p1 0 0 0
pnt p2 0.25 0 0
pnt p3 0.5 0 0
pnt p4 0.75 0 0
pnt p5 1.0 0 0

Enregistrez le fichier sous le nom beam.fbd et appuyez sur F10 pour démarrer le prétraitement. Nous verrons quelque chose comme ce qui suit



La commande pnt crée un point dans l'espace avec les coordonnées données et sa syntaxe est la suivante

pnt [ ] [x] [y] [z]

Maintenant, connectez ces points avec des lignes, en ajoutant le texte suivant au fichier

line l1 p1 p2 25
line l2 p2 p3 25
line l3 p3 p4 25
line l4 p4 p5 25

avoir reçu après avoir appuyé sur F10 l'image suivante



L'équipe

line [ ] [ 1] [ 2] [ ]

crée une ligne reliant les points qui y sont indiqués, en ajoutant des points intermédiaires divisant la ligne en un nombre spécifié de segments (dans notre cas, 25 pour chaque ligne). Cela sera utile plus tard pour la génération du réseau. Maintenant, fais la feinte avec nos oreilles

seta lines l l1 l2 l3 l4
swep lines sweeplines tra 0 0 0.1 10

Première équipe

seta [ ] [ 1] ... [ N]

combine plusieurs objets dans un ensemble avec le nom donné. En fait, c'est un analogue du regroupement d'objets. Commande suivante

swep [ ] [ ] [ ] [, ] []

Déplace l'ensemble d'objets sélectionné pour former un nouvel ensemble. Les objets mobiles sont copiés. Dans ce cas, le mouvement des points forme des lignes, le mouvement des lignes - surfaces, le mouvement des surfaces - des volumes continus. Dans notre cas, nous décalons l'ensemble des lignes de lignes le long de l'axe Z de 0,1 mètre, tandis que les lignes résultantes sont divisées en 10 segments. Nous appuyons sur F10 ... euh, et qu'est-ce que c'est?



Ghm, un écran vide ... C'est facile à réparer, il suffit d'ajouter des lignes à la fin du script

plot pa all
plus la all

Ces commandes vous indiquent de dessiner tous les points (pa) et d'ajouter toutes les lignes (la) à l'affichage, après quoi nous obtenons ce résultat



Créons maintenant des surfaces basées sur l'ensemble des lignes que nous avons créées

seta surfaces s A001 A002 A003 A004

ajout de l'affichage de ces surfaces à la toute fin du script

plus sa all




Nous allons maintenant effectuer un autre décalage, maintenant le long de l'axe Y de 0,05 mètre, développant toutes les lignes formées par le déplacement de 5 segments.

swep surfaces swepsurface tra 0.0 0.05 0.0 5

Obtenez quelque chose dans l'esprit



L'image résultante peut être tournée en maintenant le bouton gauche de la souris, et en supprimant l'affichage des points et des lignes, nous verrons quelque chose d'intelligible



Ouais ... CalculiX est loin des concepts visuels habituels familiers à l'utilisateur de masse, mais nous avons néanmoins construit la géométrie de notre poutre.

Géométrie, géométrie, mais pour la génération de maillage, nous allons faire le prochain pas - supprimer toutes les commandes de tracé et plus et encapsuler le code de génération de géométrie dans les commandes seto et setc, comme ceci

seto beam
pnt p1 0 0 0
pnt p2 0.25 0 0
pnt p3 0.5 0 0
pnt p4 0.75 0 0
pnt p5 1.0 0 0
line l1 p1 p2 25
line l2 p2 p3 25
line l3 p3 p4 25
line l4 p4 p5 25
seta lines l l1 l2 l3 l4
swep lines sweeplines tra 0 0 0.1 10
seta surfaces s A001 A002 A003 A004
swep surfaces swepsurface tra 0 0.05 0 5
setc beam

Cette paire de commandes combine toute la géométrie créée dans un certain bloc de géométrie avec le nom du faisceau. Maintenant, ce groupe géométrique peut être ignoré dans la génération de maillage, en spécifiant après tout le code de commande ci-dessus

elty beam he8
mesh beam

- Génère une grille composée de parallélépipèdes (he8) basée sur une géométrie nommée poutre. Imprimez maintenant le maillage généré dans un fichier

send beam abq

- sortie maillée dans un fichier nommé beam.msh au format du package ABAQUS FEM (il existe un tel package propriétaire de calculs FEM et CalculiX comprend son format)



Ainsi, la grille est générée, vous pouvez regarder dans le fichier beam.msh et y voir quelque chose comme ça

*NODE, NSET=Nbeam
1,0.000000000000e+000,0.000000000000e+000,1.000000000000e-001
2,0.000000000000e+000,0.000000000000e+000,9.000000000000e-002
3,0.000000000000e+000,1.000000000000e-002,9.000000000000e-002
4,0.000000000000e+000,1.000000000000e-002,1.000000000000e-001
5,1.000000000000e-002,0.000000000000e+000,1.000000000000e-001
6,1.000000000000e-002,0.000000000000e+000,9.000000000000e-002
7,1.000000000000e-002,1.000000000000e-002,9.000000000000e-002
8,1.000000000000e-002,1.000000000000e-002,1.000000000000e-001
9,0.000000000000e+000,2.000000000000e-002,9.000000000000e-002
10,0.000000000000e+000,2.000000000000e-002,1.000000000000e-001
11,1.000000000000e-002,2.000000000000e-002,9.000000000000e-002
.
.
.
.
*ELEMENT, TYPE=C3D8, ELSET=Ebeam
1, 1, 2, 3, 4, 5, 6, 7, 8
2, 4, 3, 9, 10, 8, 7, 11, 12
3, 10, 9, 13, 14, 12, 11, 15, 16
4, 14, 13, 17, 18, 16, 15, 19, 20
5, 18, 17, 21, 22, 20, 19, 23, 24
6, 5, 6, 7, 8, 25, 26, 27, 28
7, 8, 7, 11, 12, 28, 27, 29, 30
8, 12, 11, 15, 16, 30, 29, 31, 32
9, 16, 15, 19, 20, 32, 31, 33, 34

Apparemment, il s'agit d'une liste de sommets des éléments de la grille avec leurs coordonnées, suivie d'une liste de faces. Pour rendre tout cela plus beau, nous utilisons le mode interactif CalculiX. Pour ce faire, en laissant la fenêtre graphique active , entrez les commandes suivantes séquentiellement

plot f beam

- afficher toutes les faces de la géométrie

view edge off

- désactiver l'affichage des bords

view elem

- activer l'affichage des éléments de la grille. Nous complétons la saisie de chaque commande en appuyant sur Entrée, les commandes saisies sont affichées dans la fenêtre SciTE en bas à droite, comme ceci



Oui, vous ne pouvez pas appeler cela très pratique, mais nous obtenons néanmoins une image du maillage généré.



Je note que tous les points intermédiaires qui ont été créés lors de la création de la géométrie sont devenus des nœuds de maillage. Ainsi, nous avons obtenu une grille hexagonale mesurant 100 x 10 x 5 nœuds, avec une taille de bord d'élément de 10 mm. Le fichier beam.fbd que nous avons créé décrit la géométrie du problème et le processus de création du maillage.

4. Fixer des limites

Une étape importante dans l'application de la FEM est de fixer des restrictions sur le déplacement des points structurels, c'est-à-dire de prendre en compte les contraintes qui lui sont imposées. Dans notre cas, une des extrémités de la poutre est pincée, et on peut supposer que l'une de ses extrémités est complètement stationnaire. Nous devons dire au solveur quels nœuds du maillage FE sont immobiles. Nous appuyons sur F10 lorsque le fichier beam.fbd est ouvert, attendons que la fenêtre avec l'image du faisceau apparaisse



En mode interactif, entrez la commande
rot -y
plot n beam

La première équipe déploie le modèle de sorte que l'axe Y regarde loin de nous, la seconde - inclut les nœuds de dessin (n) du maillage FE. En déplaçant le modèle (en maintenant le bouton droit de la souris) et en redimensionnant l'image (en maintenant la molette de la souris), nous obtenons cette image



Maintenant, nous devons sélectionner tous les nœuds que nous voulons définir comme fixes. Pour ce faire, nous utilisons à nouveau le mode de saisie de données interactif. Nous recrutons une équipe

qadd fixed

qui commence à créer un ensemble de nœuds appelé fixe. Le curseur sur la fenêtre graphique passe en mode de sélection d'élément - il est affiché sous la forme d'une flèche avec un petit carré. Placez le curseur comme ceci



et appuyez sur la touche r. Et puis on met le curseur comme ça



et appuyez à nouveau sur r. Ainsi, nous avons formé une zone de sélection de forme rectangulaire, dont la diagonale est définie par les positions du curseur marquées en appuyant sur r. Nous sélectionnons avec ce rectangle les nœuds dont nous avons besoin se trouvant sur l'extrémité du faisceau



appuyez sur a puis sur n, en mettant en surbrillance les nœuds marqués. Un footcloth apparaîtra dans la fenêtre de la console avec une liste des nœuds sélectionnés (l'image est cliquable)



Entrez q pour quitter le mode de sélection et la commande

plus n fixed g

pour afficher les nœuds du groupe fixe en vert (g). Nous pouvons maintenant voir quels nœuds seront inclus dans la condition d'épinglage.



Maintenant, nous devons décharger ces nœuds sous forme de fichier de contraintes, qui est ensuite alimenté à l'entrée du solveur. Pour ce faire, tapez la commande

send fixed abq spc 123

- décharger un groupe de nœuds fixes sous la forme d'un fichier de contraintes au format ABAQUS (abq), restreignant le mouvement de tous les nœuds du groupe dans les trois degrés de liberté (1 - axe X, 2 - axe Y, 3 - axe Z). En conséquence, le fichier fixed_123.bou est formé, avec le contenu suivant

** BOUNDARY based on fixed
1, 1, ,
2, 1, ,
3, 1, ,
4, 1, ,
9, 1, ,
10, 1, ,
13, 1, ,
14, 1, ,
17, 1, ,
.
.
.


- en fait, il s'agit d'une énumération de tous les nœuds et du degré de liberté par lequel le mouvement d'un nœud donné est limité.

5. Affectation des charges

Après avoir sécurisé notre poutre, nous essaierons de la charger. Activer à nouveau l'affichage des visages et des éléments

plot f beam
view edge off
view elem

Orientez l'image afin que nous puissions voir la partie supérieure de l'extrémité libre du faisceau



Passons au mode de sélection d'objet

qadd load

Placez le curseur sur le visage souhaité et appuyez sur f



Le visage est surligné en violet et une description apparaît dans la fenêtre de la console pour l'ajouter au jeu de charges.

qadd load
2541 e:3873 s:6 n= 5298 5310 5312 5300

Appuyez sur a pour terminer la formation de l'ensemble, appuyez sur q pour quitter le mode de sélection. Nous appliquons une pression sur la face sélectionnée qui donne une force résultante de 10000 N. Il est facile de calculer que l'aire de la face sélectionnée est de 1 cm ² , ce qui signifie que la pression souhaitée est de 10 ⁸ Pa. Définissez cette charge avec la commande

send load abq pres 1e8

- affiche la charge dans le fichier load.dlo au format ABAQUS. Le fichier ressemble à ceci

** Pressure based on load
3873, P6, 100000000.000000

Le numéro de l'élément maillé, sa face et la valeur de pression sur cette face sont indiqués. Ainsi, la préparation des données initiales peut être considérée comme terminée.

6. Description des données d'entrée et lancement du solveur

Toutes ces données - la grille, les limitations et les charges, devraient maintenant être tirées vers l'entrée du solveur FEM, pour laquelle nous formons un fichier d'entrée de ce type

beam.inp
*HEADING
Model: CalculiX Beam Input File for Habrahabr article
*INCLUDE,INPUT=beam.msh
*BOUNDARY
*INCLUDE,INPUT=fixed_123.bou
*MATERIAL,NAME=EL
*ELASTIC
2e11,0.3
*SOLID SECTION,ELSET=Ebeam,MATERIAL=EL
*STEP
*STATIC
*DLOAD
*INCLUDE,INPUT=load.dlo
*NODE FILE
U
*EL FILE
S
*END STEP


Je vais expliquer plus en détail ce qui est quoi. Première section du dossier

*HEADING
Model: CalculiX Beam Input File for Habrahabr article
*INCLUDE,INPUT=beam.msh

définit la description de la tâche et inclut un fichier avec le faisceau.msh CE-mesh. La section suivante forme les conditions aux limites - ces relations que nous avons définies dans le fichier fixed_123.bou

*BOUNDARY
*INCLUDE,INPUT=fixed_123.bou


N'oublions pas le matériau que nous définissons comme élastique, déterminant son module d'Young et son coefficient de Poisson. Nous prenons les valeurs moyennes des aciers de construction

*MATERIAL,NAME=EL
*ELASTIC
2e11,0.3
*SOLID SECTION,ELSET=Ebeam,MATERIAL=EL

La dernière section définit le type de tâche - le calcul du chargement statique et les charges du fichier load.dlo qui sont

*STEP
*STATIC
*DLOAD
*INCLUDE,INPUT=load.dlo
*NODE FILE
U
*EL FILE
S
*END STEP


Après avoir vérifié que nous avons un onglet dans SciTE avec le fichier beam.inp, appuyez sur Ctrl + F10, lançant ainsi le solveur. Nous obtenons un échappement nous disant que CalculiX a calculé quelque chose pour nous là-bas. Échappement, pour ne pas encombrer le texte que j'apporte sous le spoiler

7. Post-traitement et analyse des décisions

Les résultats obtenus par le solveur nécessitent un traitement par le postprocesseur. Pour l'appeler, appuyez sur Maj + F10 et obtenez une fenêtre graphique avec l'image du faisceau. Cliquez sur le côté gauche de cette fenêtre, en dehors du cadre avec l'image du faisceau et obtenez le menu



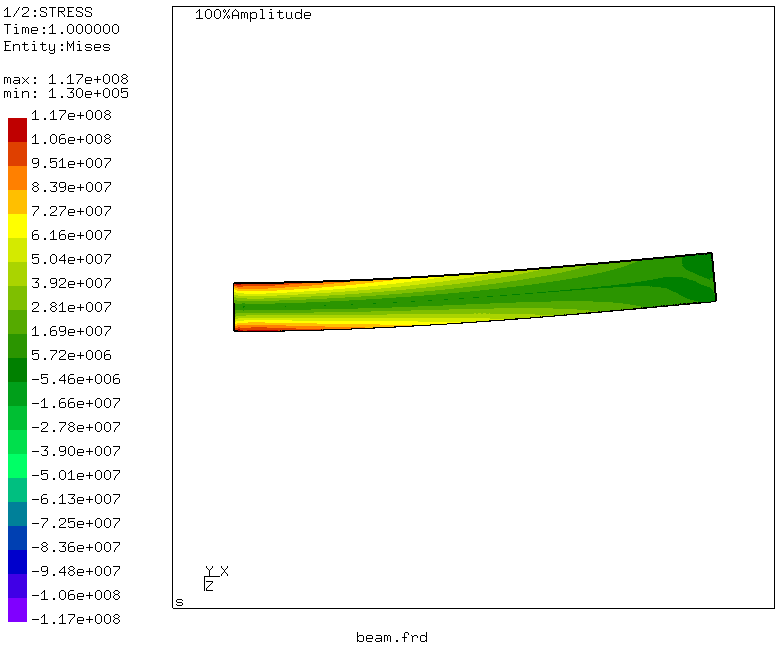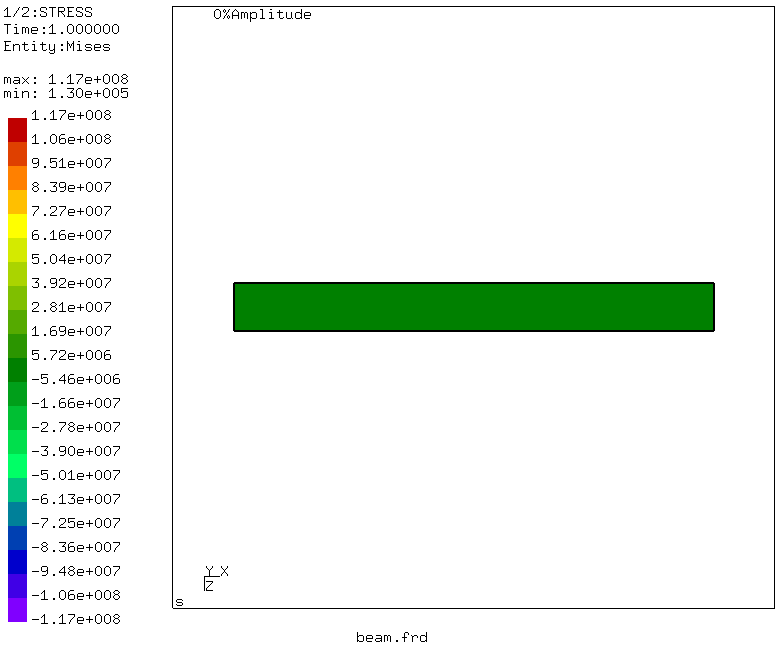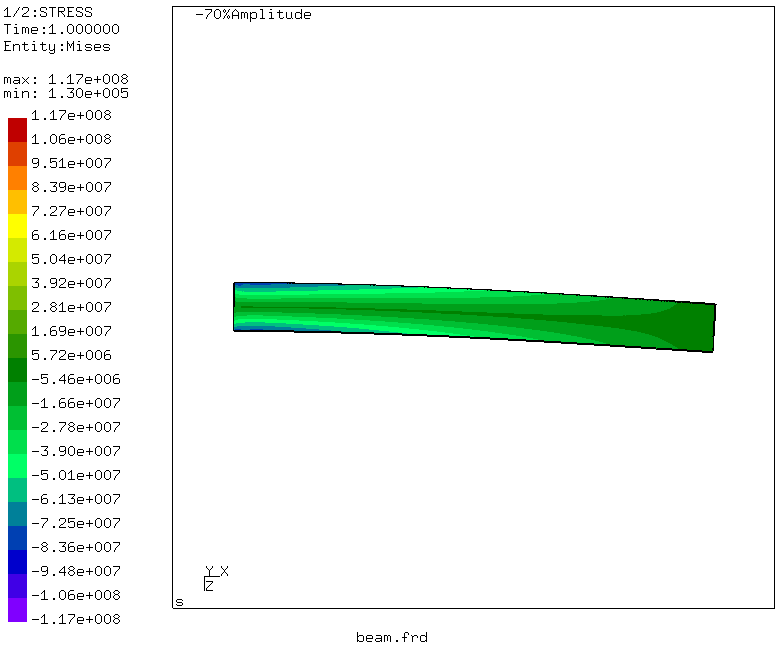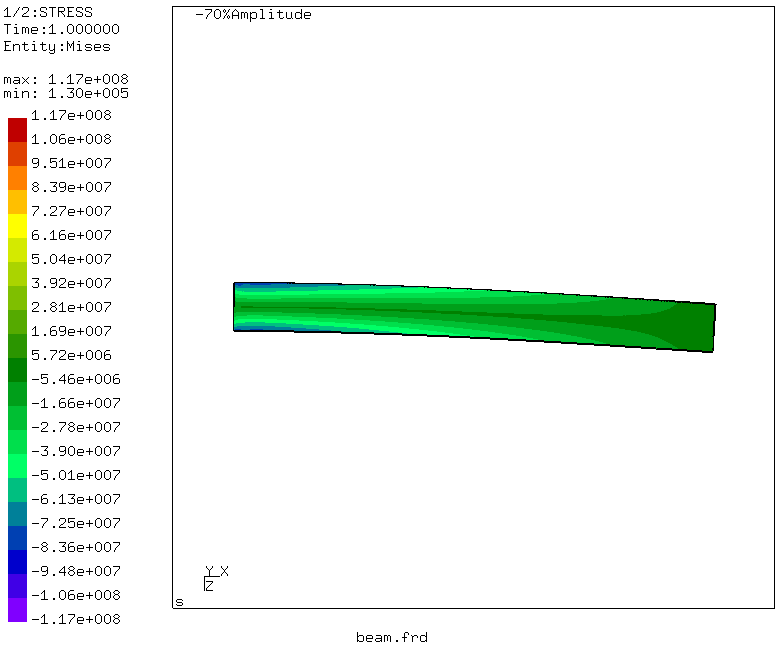
Qu'est-ce qui nous intéresse? Contraintes dans les sections de poutre - sélectionnez Jeux de données -> STRESS. Le menu disparaîtra, mais nous l'appelons à nouveau et sélectionnez Datasets -> Entities -> Mises. Par conséquent, le mode de contrainte équivalent de von Mises est activé.



Alors - le moment de vérité! La contrainte équivalente maximale dans la section du faisceau est de 117 MPa, ce qui diffère légèrement du résultat du compromis. Mais! Pour résoudre le problème de sopromat, nous n'avons pas pris en compte les contraintes tangentielles lors de la flexion et du cisaillement, mais avons calculé uniquement les contraintes normales de flexion. Qu'arrivera-t-il à la déviation? Allez dans le menu: Datasets -> DISP et Datasets -> Entities -> D3



On observe que le déplacement maximum correspond à l'extrémité chargée de la poutre et est égal à 3,96 millimètres! Magnifique et correspond à notre calcul en utilisant l'intégrale de Mohr.

Par de simples manipulations, qui peuvent être lues ici , une animation des déformations du faisceau est également générée.

Tirer des conclusions

"Euh, mec, attends une minute, quelle est la prochaine?!" Hmm, l'homme ne peut pas intégrer dans un seul article toute la variété des problèmes qui se posent en mentionnant le FEM en général, et CalculiX en particulier. L'article s'est avéré volumineux et plutôt ennuyeux. Et son but est d'expliquer deux choses dans un langage intelligible:

1. L'Open Source n'est pas passé par le logiciel d'analyse FEM
2. Étudier et utiliser ce logiciel n'est pas aussi difficile qu'il y paraît à première vue

Assez pour un article de synthèse? Je pense que oui. Pour préparer l'article, les sources suivantes ont été utilisées:

1. Calculix FEA Beam - a servi de base à tout le matériel présenté. Étant donné que l'expérience acquise par l'auteur est ajoutée ici et que tout le code a été écrit par lui lors de la rédaction de l'article, il ne s'agit pas d'une traduction, à savoir d'un tutoriel en russe
2. Manuel officiel de CalculiX

Un exemple de code est disponible sur Gitlab .

En conclusion, je note - je ne suis pas fort, je n'ai pas eu de compromis à l'université. Un peu plus tard, la vie (et l'amour!) M'a obligé à connaître ses fondements mêmes. Donc, des bévues, peut-être, sont présentes dans le texte, sur lequel j'attends des commentaires malveillants et je promets de prendre en compte tous les commentaires.

Merci de votre attention!