Numéros à virgule flottante Far West les plus rapides

Lors de la mise en œuvre d'un «lecteur», un problème s'est posé avec une précision accrue des calculs. L'algorithme de calcul a fonctionné rapidement sur les nombres à virgule flottante standard, mais lorsque les bibliothèques pour les calculs précis ont été connectées, tout a commencé à ralentir sauvagement. Dans cet article, nous considérerons les algorithmes d'expansion des nombres à virgule flottante en utilisant une approche multi-composants, grâce à laquelle il a été possible d'obtenir une accélération, car l'arithmétique flottante est implémentée sur une puce cp. Cette approche sera utile pour un calcul plus précis de la dérivée numérique, de l'inversion matricielle, du découpage polygonal ou d'autres problèmes géométriques. Il est donc possible d'émuler un flottant 64 bits sur des cartes vidéo qui ne les prennent pas en charge.

Présentation

Comme Nikluas Wirth nous a légué de garder les chiffres 0 et 1, nous les stockons donc en eux. Et est-ce que les humains vivent dans le système décimal, et les nombres apparemment ordinaires 0,1 et 0,3 ne sont pas représentables dans le système binaire par une fraction finie? Nous subissons un choc culturel lorsque nous effectuons des calculs à leur sujet. Bien sûr, des tentatives sont faites pour créer des bibliothèques pour les processeurs basés sur le système décimal et IEEE a même des formats standardisés.

Mais pour l'instant, nous prenons en compte le stockage binaire partout et effectuons tous les calculs d'argent avec des bibliothèques pour des calculs exacts, tels que bignumber, ce qui entraîne une perte de performances. Les Asiks considèrent la crypto, et dans les processeurs, il y a si peu d'espace pour cette arithmétique décimale, selon les spécialistes du marketing. Par conséquent, une approche à plusieurs composants, lorsqu'un nombre est stocké sous la forme d'une somme de nombres non transformée, est une astuce pratique et une sphère en développement actif dans le domaine de l'informatique théorique. Bien que Decker ait encore appris à se multiplier correctement, sans perte de précision, en 1971, des bibliothèques prêtes à l'emploi sont apparues beaucoup plus tard (MPFR, QD) et pas dans toutes les langues, apparemment car toutes ne prenaient pas en charge les normes IEEE, mais des preuves rigoureuses d'erreur de calcul encore plus tard, par exemple en 2017 pour l'arithmétique des mots doubles.

Arithmétique à deux mots

À quoi ça sert? Dans les temps barbus, quand il n'y avait pas de normes pour les nombres flottants, pour éviter des problèmes avec la mise en œuvre de l'arrondi, Møller est venu avec, et Knuth a prouvé plus tard qu'il y avait une sommation sans erreur. Courir de cette façon

function quickTwoSum(a, b) { let s = a + b; let z = s - a; let e = b - z; return [s, e]; } 

Dans cet algorithme, on a supposé que si $$$| a | > | b |$, alors leur somme exacte peut être représentée comme la somme de deux nombres $$$s + e$et vous pouvez les stocker par paires pour les calculs ultérieurs, et la soustraction est réduite à l'addition avec un nombre négatif.



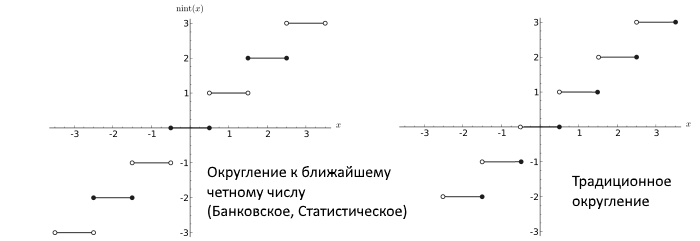
Par la suite, Dekker a montré que si des nombres à virgule flottante sont utilisés qui utilisent l'arrondi au nombre pair le plus proche (liens arrondis au plus proche à pair, ce qui est généralement une procédure correcte qui ne conduit pas à de grandes erreurs dans le processus de longs calculs et la norme IEEE), puis il y a un algorithme de multiplication sans erreur.

 function twoMult(a, b) { let A = split(a); let B = split(b); let r1 = a * b; let t1 = -r1 + A[0] * B[0]; let t2 = t1 + A[0] * B[1]; let t3 = t2 + A[1] * B[0]; return [r1, t3 + A[1] * B[1]]; } 

où split () est l'algorithme de M. Weltkamp pour diviser un nombre

 let splitter = Math.pow(2, 27) + 1; function split(a) { let t = splitter * a; let d = a - t; let xh = t + d; let xl = a - xh; return [xh, xl]; } 

en utilisant constante $$$C = 2 ^ s + 1$ce qui équivaut à un peu plus de la moitié de la longueur de la mantisse, ce qui ne conduit pas à un débordement de nombres en cours de multiplication et divise la mantisse en deux moitiés. Par exemple, avec une longueur de mot de 64 bits, la longueur de la mantisse est 53 puis s = 27.



De cette façon, Dekker a fourni l'ensemble presque complet nécessaire au calcul en arithmétique des mots doubles. Depuis, il a également été indiqué comment multiplier, diviser et mettre au carré deux nombres de deux mots.

Son algorithme quickTwoSum pour additionner deux mots doubles était partout «en ligne», et la vérification a été utilisée $$$| a | > | b |$. Sur les processeurs modernes, comme décrit dans [4], il est moins coûteux d'utiliser des opérations supplémentaires avec des nombres que de ramifier l'algorithme. Par conséquent, l'algorithme suivant est maintenant plus approprié pour ajouter deux nombres d'un seul mot

 function twoSum(a, b) { let s = a + b; let a1 = s - b; let b1 = s - a1; let da = a - a1; let db = b - b1; return [s, da + db]; } 

Et c'est donc la somme et la multiplication des nombres à double mot.

 function add22(X, Y) { let S = twoSum(X[0], Y[0]); let E = twoSum(X[1], Y[1]); let c = S[1] + E[0]; let V = quickTwoSum(S[0], c); let w = V[1] + E[1]; return quickTwoSum(V[0], w); } function mul22(X, Y) { let S = twoMult(X[0], Y[0]); S[1] += X[0] * Y[1] + X[1] * Y[0]; return quickTwoSum(S[0], S[1]); } 

De manière générale, la liste la plus complète et la plus précise des algorithmes pour l'arithmétique des mots doubles, les limites d'erreur théorique et la mise en œuvre pratique sont décrits dans le lien [3] de 2017. Par conséquent, si vous êtes intéressé, je vous recommande fortement d'y aller directement. En général, un algorithme pour quadruple mot est donné dans [6] et dans [5] pour une extension multicomposant de longueur arbitraire. Seulement là, après chaque opération, le processus de renormalisation est utilisé, ce qui n'est pas toujours optimal pour les petites tailles, et la précision des calculs dans QD n'est pas strictement définie. En général, il convient bien sûr de réfléchir aux limites d'applicabilité de ces approches.

Histoires d'horreur javascript-a. Comparaison de decimal.js vs bignumber.js vs big.js.

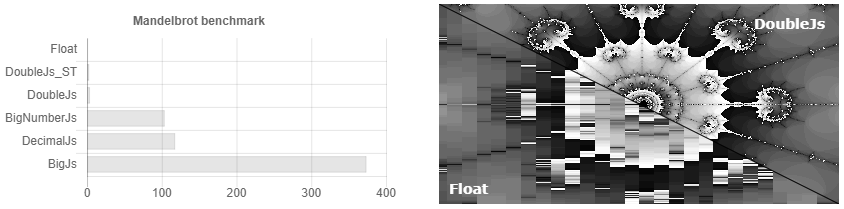
Il se trouve que presque toutes les bibliothèques pour les calculs exacts en js ont été écrites par une seule personne. L'illusion du choix est créée, bien qu'elles soient presque toutes les mêmes. De plus, la documentation n'indique pas explicitement que si vous n'arrondissez pas les nombres après chaque opération de multiplication / division, la taille de votre nombre doublera tout le temps et la complexité de l'algorithme peut devenir facile en x3500. Par exemple, une comparaison de leur temps de calcul pourrait ressembler à ceci si vous n'avez pas arrondi les nombres.



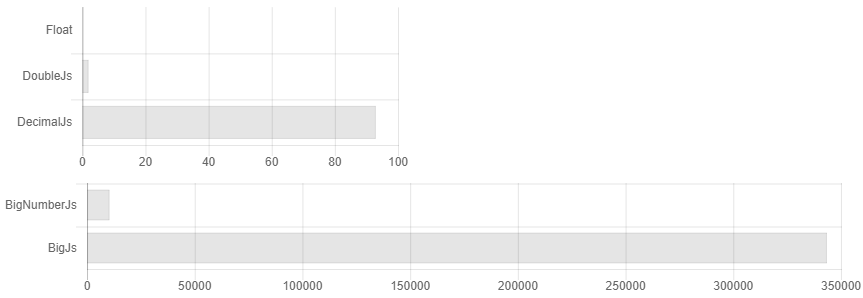
Autrement dit, vous définissez la précision à 32 décimales et ... Oups, vous avez déjà 64 chiffres, 128. Nous pensons très précisément! 256, 512 ... Mais j'en ai réglé 32! .. 1024, 2048 ... Quelque chose comme ça apparaît au dessus de 3500 fois. La documentation indique que si vous avez des calculs scientifiques, alors probablement decimal.js est mieux pour vous. Bien qu'en fait, si vous arrondissez périodiquement, Bignumber.js fonctionne un peu plus rapidement pour les calculs scientifiques (voir Fig. 1). Qui doit compter les centièmes de centime s'ils ne peuvent pas être donnés en monnaie? Y a-t-il un cas où j'ai besoin de stocker plus de numéros indiqués et que je ne peux pas sortir avec quelques caractères supplémentaires? Comment faut-il prendre le sinus d'un tel nombre de monstres, alors que personne ne connaît la stricte précision de la convergence de la série de Taylor pour des nombres arbitraires? En général, il n'y a pas de soupçons non fondés qu'il soit possible d'augmenter la vitesse de calcul là-bas, en utilisant des algorithmes de multiplication de Schoenhage-Strassen et en trouvant le sinus avec des calculs Cordic, par exemple.

Double.js

Je voudrais dire, bien sûr, que Double.js compte rapidement et avec précision. Mais ce n'est pas tout à fait vrai, c'est-à-dire qu'il est 10 fois plus rapide qu'il le considère, mais ce n'est pas toujours exact. Par exemple, 0.3-0.1, il peut le traiter, passant en double stockage et vice versa. Mais le nombre Pi peut être résolu avec une double précision de près de 32 chiffres et cela ne fonctionne pas en arrière. Une erreur est générée le 16, comme si un débordement se produisait. En général, j'exhorte la communauté js à travailler ensemble pour essayer de résoudre le problème de l'analyse, car je suis coincé. J'ai essayé d'analyser numériquement et de diviser en double précision, comme dans QD, de diviser en lots de 16 chiffres et de diviser en double précision, de diviser la mantisse en utilisant Big.js comme dans l'une des bibliothèques Julia. Maintenant, je pèche sur un bogue dans .parseFloat (), car les normes IEEE avec arrondi à l'entier le plus proche sont prises en charge même avec ECMAScript 1. Bien que vous puissiez bien sûr essayer de lier le tampon binaire et regarder tous les 0 et 1. En général, si vous pouvez résoudre ce problème, alors il sera alors possible de faire des calculs avec une précision arbitraire avec une accélération en x10-x20 à partir de bignumber.js. Cependant, de nombreux Mandelbrot rendent déjà la qualité et vous pouvez l'utiliser pour des tâches géométriques.

Un an plus tard, je suis revenu ici et j'ai toujours résolu un problème d'analyse. Le problème n'était que d'une précision insuffisante, lorsqu'il était multiplié par 10 ^ (- n). Tous les algorithmes ont été révisés à partir de zéro et fonctionnent désormais avec une précision et une vitesse effrayantes.



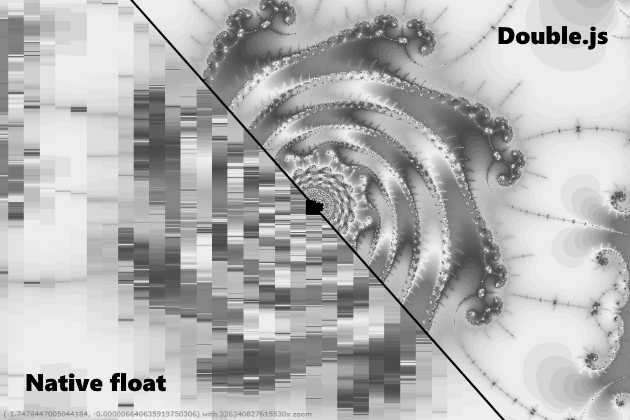
Voici un lien vers la lib , il y a un benchmark interactif et un bac à sable où vous pouvez jouer avec.

Sources utilisées

1. O. Møller. Quasi double précision en arithmétique à virgule flottante. , 1965.
2. Theodorus Dekker. Une technique à virgule flottante pour étendre la précision disponible , 1971. [ Visionneuse ]
3. Mioara Joldes, Jean-Michel Muller, Valentina Popescu. Limites d'erreur strictes et rigoureuses pour les blocs de construction de base de l'arithmétique des mots doubles , 2017. [ PDF ]
4. Muller, J.-M. Brisebarre, N. de Dinechin, etc. Manuel d'arithmétique à virgule flottante, chapitre 14, 2010.
5. Jonathan Shewchuk. Prédicats géométriques adaptatifs à virgule flottante robustes , 1964. [ PDF ]
6. Yozo Hida, Xiaoye Li, David Bailey. Bibliothèque d'arithmétique double-double et quad-double , 2000. [ PDF ]